數(shù)據(jù)結(jié)構(gòu)快速盤點 - 非線性結(jié)構(gòu)

PS：為了更好的閱讀體驗，推薦閱讀原文，到我的博客中閱讀。

那么有了線性結(jié)構(gòu)，我們?yōu)槭裁催€需要非線性結(jié)構(gòu)呢？?答案是為了高效地兼顧靜態(tài)操作和動態(tài)操作。大家可以對照各種數(shù)據(jù)結(jié)構(gòu)的各種操作的復雜度來直觀感受一下。

樹

樹的應用同樣非常廣泛，小到文件系統(tǒng)，大到因特網(wǎng)，組織架構(gòu)等都可以表示為樹結(jié)構(gòu)，而在我們前端眼中比較熟悉的 DOM 樹也是一種樹結(jié)構(gòu)，而 HTML 作為一種 DSL 去描述這種樹結(jié)構(gòu)的具體表現(xiàn)形式。如果你接觸過 AST，那么 AST 也是一種樹，XML 也是樹結(jié)構(gòu)。。。樹的應用遠比大多數(shù)人想象的要得多。

樹其實是一種特殊的圖，是一種無環(huán)連通圖，是一種極大無環(huán)圖，也是一種極小連通圖。

從另一個角度看，樹是一種遞歸的數(shù)據(jù)結(jié)構(gòu)。而且樹的不同表示方法，比如不常用的長子 + 兄弟法，對于 你理解樹這種數(shù)據(jù)結(jié)構(gòu)有著很大用處， 說是一種對樹的本質(zhì)的更深刻的理解也不為過。

樹的基本算法有前中后序遍歷和層次遍歷，有的同學對前中后這三個分別具體表現(xiàn)的訪問順序比較模糊，其實當初我也是一樣的，后面我學到了一點，你只需要記住：所謂的前中后指的是根節(jié)點的位置，其他位置按照先左后右排列即可。比如前序遍歷就是根左右, 中序就是左根右，后序就是左右根， 很簡單吧？

我剛才提到了樹是一種遞歸的數(shù)據(jù)結(jié)構(gòu)，因此樹的遍歷算法使用遞歸去完成非常簡單，幸運的是樹的算法基本上都要依賴于樹的遍歷。?但是遞歸在計算機中的性能一直都有問題，因此掌握不那么容易理解的"命令式地迭代"遍歷算法在某些情況下是有用的。如果你使用迭代式方式去遍歷的話，可以借助上面提到的棧來進行，可以極大減少代碼量。

如果使用棧來簡化運算，由于棧是 FILO 的，因此一定要注意左右子樹的推入順序。

樹的重要性質(zhì)：

• 如果樹有 n 個頂點，那么其就有 n - 1 條邊，這說明了樹的頂點數(shù)和邊數(shù)是同階的。
• 任何一個節(jié)點到根節(jié)點存在唯一路徑, 路徑的長度為節(jié)點所處的深度

實際使用的樹有可能會更復雜，比如使用在游戲中的碰撞檢測可能會用到四叉樹或者八叉樹。以及 k 維的樹結(jié)構(gòu)?k-d 樹等。

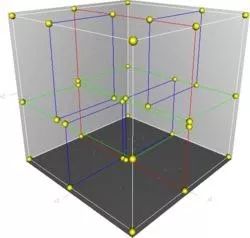（圖片來自 https://zh.wikipedia.org/wiki/K-d%E6%A0%91）

二叉樹

二叉樹是節(jié)點度數(shù)不超過二的樹，是樹的一種特殊子集，有趣的是二叉樹這種被限制的樹結(jié)構(gòu)卻能夠表示和實現(xiàn)所有的樹， 它背后的原理正是長子 + 兄弟法，用鄧老師的話說就是二叉樹是多叉樹的特例，但在有根且有序時，其描述能力卻足以覆蓋后者。

實際上， 在你使用長子 + 兄弟法表示樹的同時，進行 45 度角旋轉(zhuǎn)即可。

一個典型的二叉樹：

標記為 7 的節(jié)點具有兩個子節(jié)點, 標記為 2 和 6; 一個父節(jié)點,標記為 2,作為根節(jié)點, 在頂部,沒有父節(jié)點。

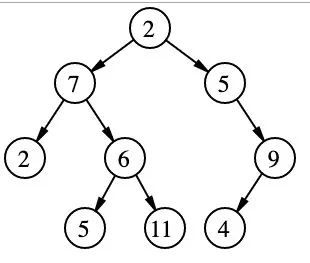
(圖片來自 https://github.com/trekhleb/javascript-algorithms/blob/master/src/data-structures/tree/README.zh-CN.md)

對于一般的樹，我們通常會去遍歷，這里又會有很多變種。

下面我列舉一些二叉樹遍歷的相關算法:

• 94.binary-tree-inorder-traversal
• 102.binary-tree-level-order-traversal
• 103.binary-tree-zigzag-level-order-traversal
• 144.binary-tree-preorder-traversal
• 145.binary-tree-postorder-traversal
• 199.binary-tree-right-side-view

相關概念：

• 真二叉樹 （所有節(jié)點的度數(shù)只能是偶數(shù)，即只能為 0 或者 2）

另外我也專門開設了二叉樹的遍歷章節(jié), 具體細節(jié)和算法可以去那里查看。

堆

堆其實是一種優(yōu)先級隊列，在很多語言都有對應的內(nèi)置數(shù)據(jù)結(jié)構(gòu)，很遺憾 javascript 沒有這種原生的數(shù)據(jù)結(jié)構(gòu)。?不過這對我們理解和運用不會有影響。

堆的特點：

• 在一個 最小堆(min heap) 中, 如果 P 是 C 的一個父級節(jié)點, 那么 P 的 key(或 value)應小于或等于 C 的對應值. 正因為此，堆頂元素一定是最小的，我們會利用這個特點求最小值或者第 k 小的值。

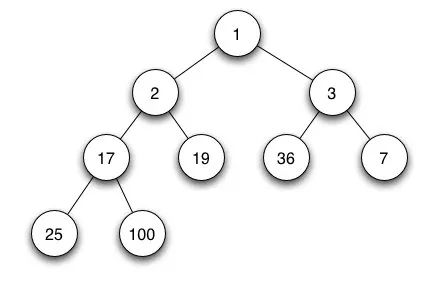
• 在一個 最大堆(max heap) 中, P 的 key(或 value)大于 C 的對應值。

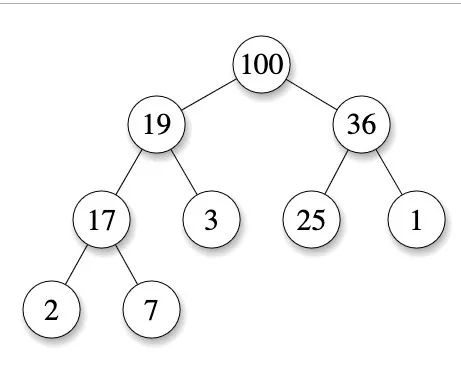
需要注意的是優(yōu)先隊列不僅有堆一種，還有更復雜的，但是通常來說，我們會把兩者做等價。

相關算法：

• 295.find-median-from-data-stream

二叉查找樹

二叉排序樹（Binary Sort Tree），又稱二叉查找樹（Binary Search Tree），亦稱二叉搜索樹。

二叉查找樹具有下列性質(zhì)的二叉樹：

• 若左子樹不空，則左子樹上所有節(jié)點的值均小于它的根節(jié)點的值；
• 若右子樹不空，則右子樹上所有節(jié)點的值均大于它的根節(jié)點的值；
• 左、右子樹也分別為二叉排序樹；
• 沒有鍵值相等的節(jié)點。

對于一個二叉查找樹，常規(guī)操作有插入，查找，刪除，找父節(jié)點，求最大值，求最小值。

二叉查找樹，之所以叫查找樹就是因為其非常適合查找，舉個例子， 如下一顆二叉查找樹，我們想找節(jié)點值小于且最接近 58 的節(jié)點，搜索的流程如圖所示：

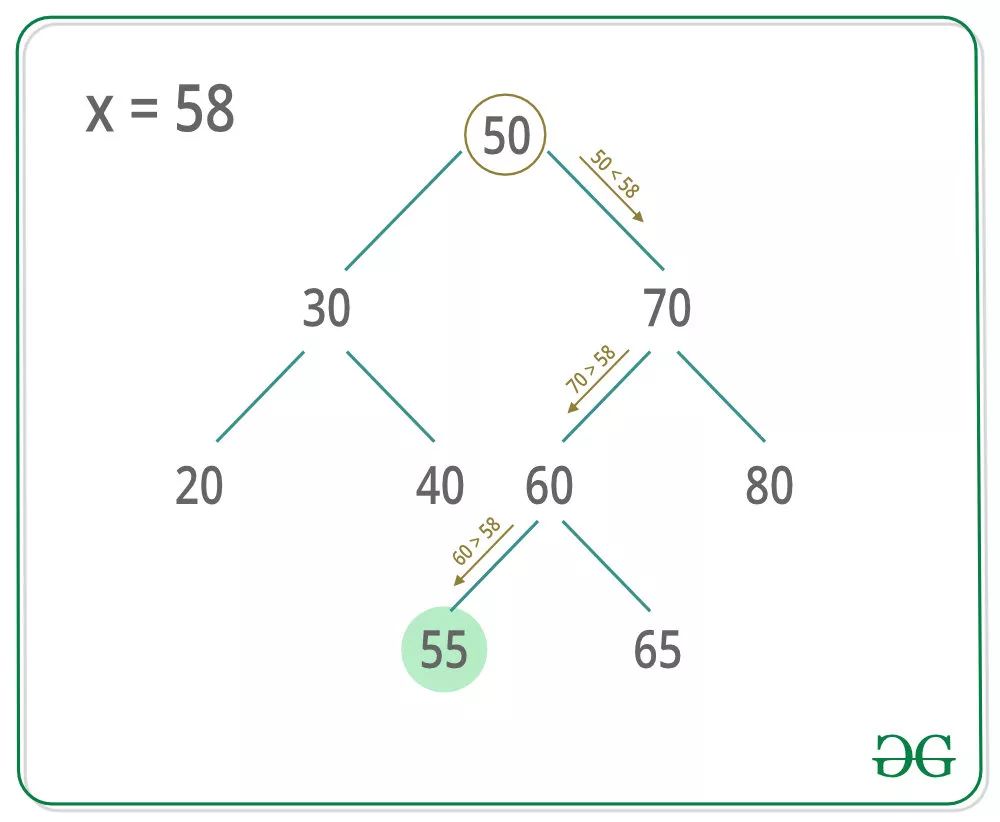（圖片來自 https://www.geeksforgeeks.org/floor-in-binary-search-tree-bst/）

另外我們二叉查找樹有一個性質(zhì)是：?其中序遍歷的結(jié)果是一個有序數(shù)組。?有時候我們可以利用到這個性質(zhì)。

相關題目：

• 98.validate-binary-search-tree

二叉平衡樹

平衡樹是計算機科學中的一類數(shù)據(jù)結(jié)構(gòu)，為改進的二叉查找樹。一般的二叉查找樹的查詢復雜度取決于目標結(jié)點到樹根的距離（即深度），因此當結(jié)點的深度普遍較大時，查詢的均攤復雜度會上升。為了實現(xiàn)更高效的查詢，產(chǎn)生了平衡樹。

在這里，平衡指所有葉子的深度趨于平衡，更廣義的是指在樹上所有可能查找的均攤復雜度偏低。

一些數(shù)據(jù)庫引擎內(nèi)部就是用的這種數(shù)據(jù)結(jié)構(gòu)，其目標也是將查詢的操作降低到 logn（樹的深度），可以簡單理解為樹在數(shù)據(jù)結(jié)構(gòu)層面構(gòu)造了二分查找算法。

基本操作：

• 旋轉(zhuǎn)

• 插入

• 刪除

• 查詢前驅(qū)

• 查詢后繼

AVL

是最早被發(fā)明的自平衡二叉查找樹。在 AVL 樹中，任一節(jié)點對應的兩棵子樹的最大高度差為 1，因此它也被稱為高度平衡樹。查找、插入和刪除在平均和最壞情況下的時間復雜度都是 {\displaystyle O(\log {n})} O(\log{n})。增加和刪除元素的操作則可能需要借由一次或多次樹旋轉(zhuǎn)，以實現(xiàn)樹的重新平衡。AVL 樹得名于它的發(fā)明者 G. M. Adelson-Velsky 和 Evgenii Landis，他們在 1962 年的論文 An algorithm for the organization of information 中公開了這一數(shù)據(jù)結(jié)構(gòu)。?節(jié)點的平衡因子是它的左子樹的高度減去它的右子樹的高度（有時相反）。帶有平衡因子 1、0 或 -1 的節(jié)點被認為是平衡的。帶有平衡因子 -2 或 2 的節(jié)點被認為是不平衡的，并需要重新平衡這個樹。平衡因子可以直接存儲在每個節(jié)點中，或從可能存儲在節(jié)點中的子樹高度計算出來。

紅黑樹

在 1972 年由魯?shù)婪颉へ悹柊l(fā)明，被稱為"對稱二叉 B 樹"，它現(xiàn)代的名字源于 Leo J. Guibas 和 Robert Sedgewick 于 1978 年寫的一篇論文。紅黑樹的結(jié)構(gòu)復雜，但它的操作有著良好的最壞情況運行時間，并且在實踐中高效：它可以在 {\displaystyle O(\log {n})} O(\log{n})時間內(nèi)完成查找，插入和刪除，這里的 n 是樹中元素的數(shù)目

字典樹(前綴樹)

又稱 Trie 樹，是一種樹形結(jié)構(gòu)。典型應用是用于統(tǒng)計，排序和保存大量的字符串（但不僅限于字符串），所以經(jīng)常被搜索引擎系統(tǒng)用于文本詞頻統(tǒng)計。它的優(yōu)點是：利用字符串的公共前綴來減少查詢時間，最大限度地減少無謂的字符串比較，查詢效率比哈希樹高。

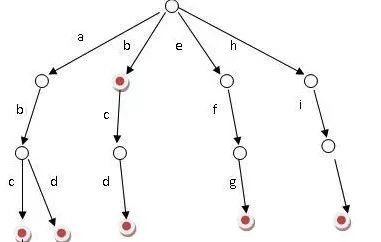
(圖來自 https://baike.baidu.com/item/%E5%AD%97%E5%85%B8%E6%A0%91/9825209?fr=aladdin) 它有 3 個基本性質(zhì)：

• 根節(jié)點不包含字符，除根節(jié)點外每一個節(jié)點都只包含一個字符；
• 從根節(jié)點到某一節(jié)點，路徑上經(jīng)過的字符連接起來，為該節(jié)點對應的字符串；
• 每個節(jié)點的所有子節(jié)點包含的字符都不相同。

immutable 與 字典樹

immutableJS的底層就是share + tree. 這樣看的話，其實和字典樹是一致的。

相關算法：

• 208.implement-trie-prefix-tree

圖

前面講的數(shù)據(jù)結(jié)構(gòu)都可以看成是圖的特例。?前面提到了二叉樹完全可以實現(xiàn)其他樹結(jié)構(gòu)， 其實有向圖也完全可以實現(xiàn)無向圖和混合圖，因此有向圖的研究一直是重點考察對象。

圖論〔Graph Theory〕是數(shù)學的一個分支。它以圖為研究對象。圖論中的圖是由若干給定的點及連接兩點的線所構(gòu)成的圖形，這種圖形通常用來描述某些事物之間的某種特定關系，用點代表事物，用連接兩點的線表示相應兩個事物間具有這種關系。

圖的表示方法

• 鄰接矩陣(常見)

空間復雜度 O(n^2),n 為頂點個數(shù)。

優(yōu)點：

1. 直觀，簡單。

2. 適用于稠密圖

3. 判斷兩個頂點是否連接，獲取入度和出度以及更新度數(shù)，時間復雜度都是 O(1)

• 關聯(lián)矩陣
• 鄰接表

對于每個點，存儲著一個鏈表，用來指向所有與該點直接相連的點 對于有權(quán)圖來說，鏈表中元素值對應著權(quán)重

例如在無向無權(quán)圖中：

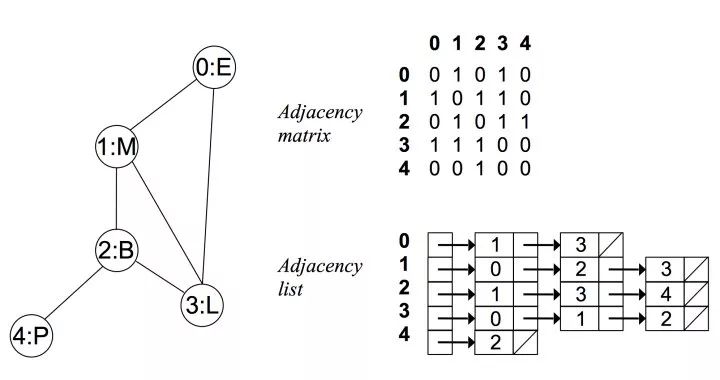（圖片來自 https://zhuanlan.zhihu.com/p/25498681）

可以看出在無向圖中，鄰接矩陣關于對角線對稱，而鄰接鏈表總有兩條對稱的邊 而在有向無權(quán)圖中：

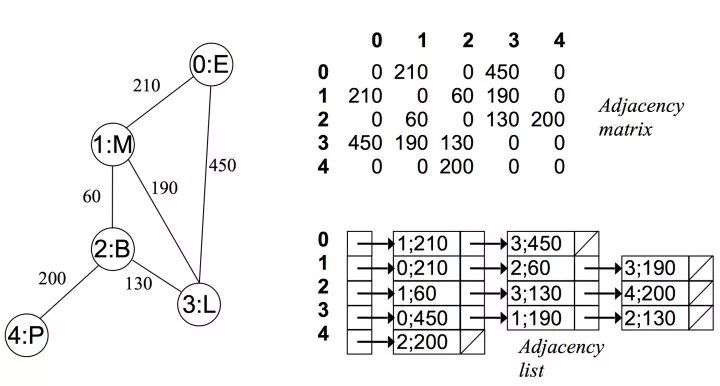
（圖片來自 https://zhuanlan.zhihu.com/p/25498681）

圖的遍歷

圖的遍歷就是要找出圖中所有的點，一般有以下兩種方法：

1. 深度優(yōu)先遍歷：(Depth First Search, DFS)

深度優(yōu)先遍歷圖的方法是，從圖中某頂點 v 出發(fā)， 不斷訪問鄰居， 鄰居的鄰居直到訪問完畢。

1. 廣度優(yōu)先搜索：(Breadth First Search, BFS)

廣度優(yōu)先搜索，可以被形象地描述為 "淺嘗輒止"，它也需要一個隊列以保持遍歷過的頂點順序，以便按出隊的順序再去訪問這些頂點的鄰接頂點。

??看完三件事

如果你覺得這篇內(nèi)容對你挺有啟發(fā)，我想邀請你幫我三個小忙：

1. 點贊，讓更多的人也能看到介紹內(nèi)容（收藏不點贊，都是耍流氓-_-）
2. 關注公眾號“前端勸退師”，不定期分享原創(chuàng)知識。
3. 也看看其他文章

勸退師個人微信：huab119

也可以來我的GitHub博客里拿所有文章的源文件：

前端勸退指南：https：//github.com/roger-hiro/BlogFN一起玩耍呀。

相關閱讀：數(shù)據(jù)結(jié)構(gòu)快速盤點 - 線性結(jié)構(gòu)