【特征工程】17種將離散特征轉(zhuǎn)化為數(shù)字特征的方法

作者 | Samuele Mazzanti?

編譯 | VK?

來(lái)源 | Towards Data Science

“你知道哪種梯度提升算法？”

“Xgboost，LightGBM，Catboost，HistGradient。”

“你知道哪些離散變量的編碼？”

“one-hot”

在一次數(shù)據(jù)科學(xué)面試中聽(tīng)到這樣的對(duì)話(huà)我不會(huì)感到驚訝。不過(guò)，這將是相當(dāng)驚人的，「因?yàn)橹挥幸恍〔糠謹(jǐn)?shù)據(jù)科學(xué)項(xiàng)目涉及機(jī)器學(xué)習(xí)，而實(shí)際上所有這些項(xiàng)目都涉及一些離散數(shù)據(jù)」。

?

離散變量的編碼是將一個(gè)離散列轉(zhuǎn)換為一個(gè)（或多個(gè)）數(shù)字列的過(guò)程。

?

這是必要的，因?yàn)橛?jì)算機(jī)處理數(shù)字比處理字符串更容易。為什么？因?yàn)橛脭?shù)字很容易找到關(guān)系（比如“大”、“小”、“雙”、“半”）。然而，當(dāng)給定字符串時(shí)，計(jì)算機(jī)只能說(shuō)出它們是“相等”還是“不同”。

然而，盡管離散變量的編碼有影響，但它很容易被數(shù)據(jù)科學(xué)從業(yè)者忽視。

?

離散變量的編碼是一個(gè)令人驚訝的被低估的話(huà)題。

?

這就是為什么我決定深化編碼算法的知識(shí)。我從一個(gè)名為“category_encoders”的Python庫(kù)開(kāi)始（這是Github鏈接：https://github.com/scikit-learn-contrib/category_encoders）。使用它非常簡(jiǎn)單：

!pip?install?category_encoders

import?category_encoders?as?ce

ce.OrdinalEncoder().fit_transform(x)

這篇文章是對(duì)庫(kù)中包含的17種編碼算法的演練。對(duì)于每種算法，我用幾行代碼提供了簡(jiǎn)短的解釋和Python實(shí)現(xiàn)。其目的不是要重新發(fā)明輪子，而是要認(rèn)識(shí)到算法是如何工作的。畢竟，

?

“除非你能寫(xiě)代碼，否則你不懂”。

?

并非所有編碼都是相同的

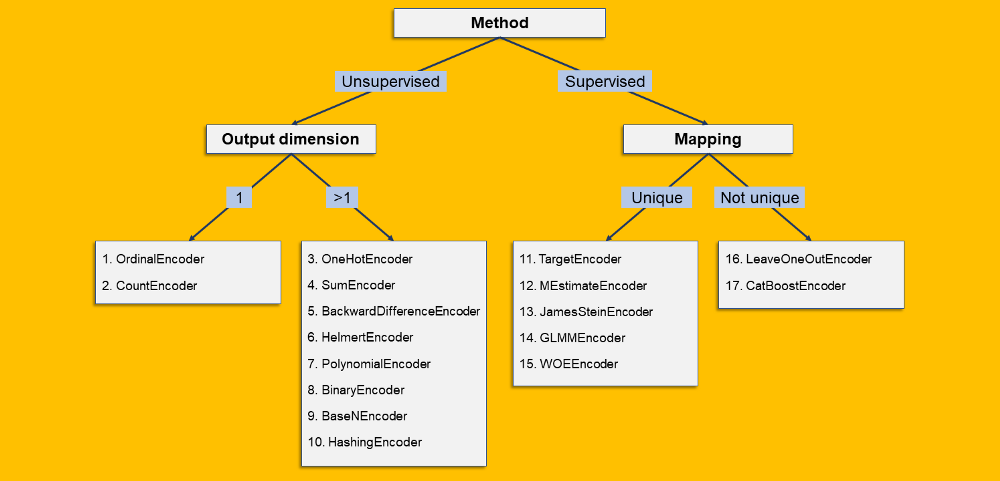
我根據(jù)17種編碼算法的一些特點(diǎn)對(duì)它們進(jìn)行了分類(lèi)。類(lèi)似決策樹(shù)：

分割點(diǎn)為：

• 「監(jiān)督/無(wú)監(jiān)督」：當(dāng)編碼完全基于離散列時(shí)，它是無(wú)監(jiān)督的。如果編碼是基于原始列和第二列（數(shù)字）的某個(gè)函數(shù)，則它是監(jiān)督的。
• 「輸出維度」：分類(lèi)列的編碼可能產(chǎn)生一個(gè)數(shù)值列（輸出維度=1）或多個(gè)數(shù)值列（輸出維度>1）。
• 「映射」：如果每個(gè)等級(jí)都有相同的輸出-無(wú)論是標(biāo)量（例如OrdinalEncoder）還是數(shù)組（例如onehotcoder），那么映射是唯一的。相反，如果允許同一等級(jí)具有不同的可能輸出，則映射不是唯一的。

17種離散編碼算法

1.「OrdinalEncoder」

每個(gè)等級(jí)都映射到一個(gè)整數(shù)，從1到L（其中L是等級(jí)數(shù)）。在這種情況下，我們使用了字母順序，但任何其他自定義順序都是可以接受的。

sorted_x?=?sorted(set(x))
ordinal_encoding?=?x.replace(dict(zip(sorted_x,?range(1,?len(sorted_x)?+?1))))

你可能認(rèn)為該編碼是沒(méi)有意義的，尤其是當(dāng)?shù)燃?jí)沒(méi)有內(nèi)在順序的時(shí)候。你是對(duì)的！實(shí)際上，它只是一種方便的表示，通常用于節(jié)省內(nèi)存，或作為其他類(lèi)型編碼的中間步驟。

2.CountEncoder

每個(gè)等級(jí)都映射到該級(jí)別的觀(guān)察數(shù)。

count_encoding?=?x.replace(x.value_counts().to_dict())

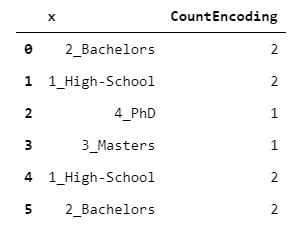
這種編碼可以作為每個(gè)級(jí)別的“可信度”的指標(biāo)。例如，一個(gè)機(jī)器學(xué)習(xí)算法可能會(huì)自動(dòng)決定只考慮其計(jì)數(shù)高于某個(gè)閾值的級(jí)別所帶來(lái)的信息。

3.OneHotEncoder

編碼算法中最常用的。每個(gè)級(jí)別映射到一個(gè)偽列（即0/1的列），指示該行是否攜帶屬于該級(jí)別。

one_hot_encoding?=?ordinal_encoding.apply(lambda?oe:?pd.Series(np.diag(np.ones(len(set(x))))[oe?-?1].astype(int)))

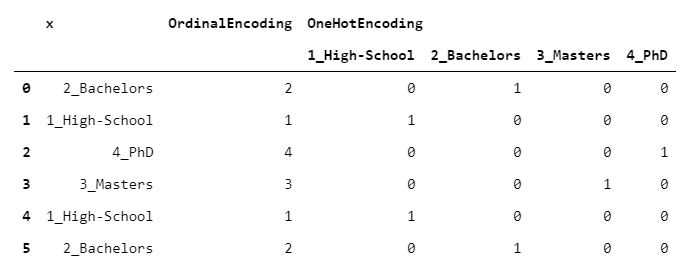
這意味著，雖然你的輸入是一個(gè)單獨(dú)的列，但是你的輸出由L列組成（原始列的每個(gè)級(jí)別對(duì)應(yīng)一個(gè)列）。這就是為什么OneHot編碼應(yīng)該小心處理：你最終得到的數(shù)據(jù)幀可能比原來(lái)的大得多。

一旦數(shù)據(jù)是OneHot編碼，它就可以用于任何預(yù)測(cè)算法。為了使事情一目了然，讓我們對(duì)每一個(gè)等級(jí)進(jìn)行一次觀(guān)察。

假設(shè)我們觀(guān)察到一個(gè)目標(biāo)變量，叫做y，包含每個(gè)人的收入（以千美元計(jì)）。讓我們用線(xiàn)性回歸（OLS）來(lái)擬合數(shù)據(jù)。

為了使結(jié)果易于閱讀，我在表的側(cè)面附加了OLS系數(shù)。

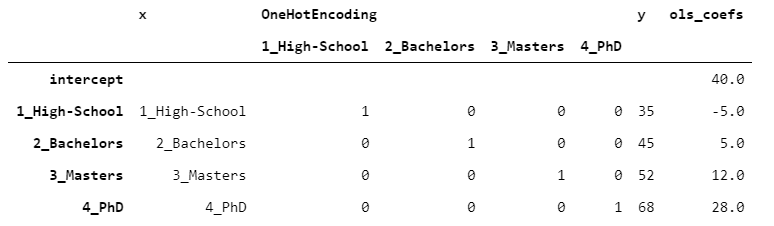
在OneHot編碼的情況下，截距沒(méi)有特定的意義。在這種情況下，由于我們每層只有一個(gè)觀(guān)測(cè)值，通過(guò)加上截距和乘上系數(shù)，我們得到y(tǒng)的精確值（沒(méi)有誤差）。

4.SumEncoder

下面的代碼一開(kāi)始可能有點(diǎn)晦澀難懂。但是不要擔(dān)心：在這種情況下，理解如何獲得編碼并不重要，而是如何使用它。

sum_encoding?=?one_hot_encoding.iloc[:,?:-1].apply(lambda?row:?row?if?row.sum()?==?1?else?row.replace(0,?-1),?axis?=?1)

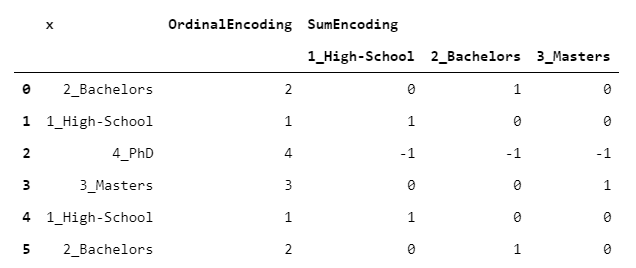
SumEncoder屬于一個(gè)名為“對(duì)比度編碼”的類(lèi)。這些編碼被設(shè)計(jì)成在回歸問(wèn)題中使用時(shí)具有特定的行為。換句話(huà)說(shuō)，如果你想讓回歸系數(shù)有一些特定的屬性，你可以使用其中的一種編碼。

特別是，當(dāng)你希望回歸系數(shù)加起來(lái)為0時(shí)，使用SumEncoder。如果我們采用之前的相同數(shù)據(jù)并擬合OLS，我們得到的結(jié)果是：

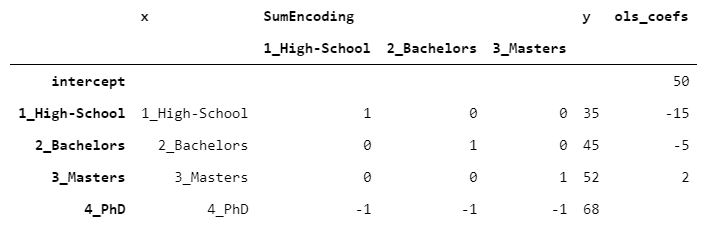
這一次，截距對(duì)應(yīng)于y的平均值。此外，通過(guò)取最后一級(jí)的y并從截距（68-50）中減去它，我們得到18，這與剩余系數(shù)之和（-15-5+2=-18）正好相反。這正是我前面提到的SumEncoder的屬性。

5.BackwardDifferenceEncoder

另一種對(duì)比度編碼。

這個(gè)編碼器對(duì)序數(shù)變量很有用，也就是說(shuō)，可以用有意義的方式對(duì)其等級(jí)進(jìn)行排序的變量。BackwardDifferenceEncoder設(shè)計(jì)用于比較相鄰的等級(jí)。

backward_difference_encoding?=?ordinal_encoding.apply(
????lambda?oe:?pd.Series(
????????[i?/?len(set(x))?for?i?in?range(1,?oe)]?+?[-?i?/?len(set(x))?for?i?in?range(len(set(x))?-?oe,?0,?-1)]))

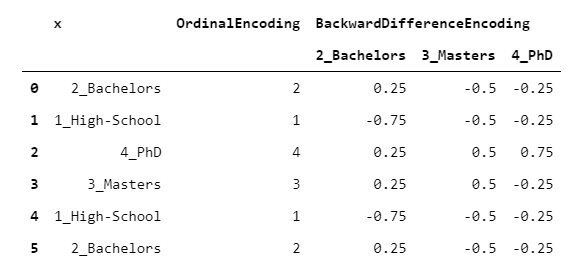
假設(shè)你有一個(gè)有序變量（例如教育水平），你想知道它與一個(gè)數(shù)字變量（例如收入）之間的關(guān)系。比較每一個(gè)連續(xù)的水平（例如學(xué)士與高中，碩士與學(xué)士）與目標(biāo)變量的關(guān)系可能很有趣。這就是BackwardDifferenceEncoder的設(shè)計(jì)目的。讓我們看一個(gè)例子，使用相同的數(shù)據(jù)。

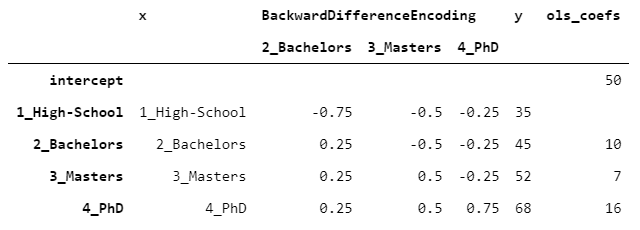
截距與y的平均值一致。學(xué)士的系數(shù)為10，因?yàn)閷W(xué)士的y比高中高10，碩士的系數(shù)等于7，因?yàn)榇T士的y比單身漢高7，依此類(lèi)推。

6.HelmertEncoder

HelmertEncoder與BackwardDifferenceEncoder非常相似，但不是只與前一個(gè)進(jìn)行比較，而是將每個(gè)級(jí)別與之前的所有級(jí)別進(jìn)行比較。

helmert_encoding?=?ordinal_encoding.apply(
????lambda?oe:?pd.Series([0]?*?(oe?-?2)?+?([oe?-?1]?if?oe?>?1?else?[])?+?[-1]?*?(len(set(x))?-?oe))
).div(pd.Series(range(2,len(set(x))?+?1)))

]

讓我們看看OLS模型能給我們帶來(lái)什么：

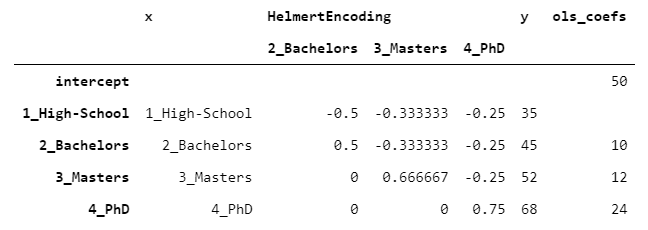
PhD的系數(shù)是24，因?yàn)镻hD比之前水平的平均值高24-（（35+45+52）/3）=24。同樣的道理適用于所有的等級(jí)。

7.PolynomialEncoder

另一種對(duì)比編碼。

顧名思義，PolynomialEncoder被設(shè)計(jì)用來(lái)量化目標(biāo)變量相對(duì)于離散變量的線(xiàn)性、二次和三次行為。

def?do_polynomial_encoding(order):
????#?代碼來(lái)自https://github.com/pydata/patsy/blob/master/patsy/contrasts.py
????n?=?len(set(x))
????scores?=?np.arange(n)
????scores?=?np.asarray(scores,?dtype=float)
????scores?-=?scores.mean()
????raw_poly?=?scores.reshape((-1,?1))?**?np.arange(n).reshape((1,?-1))
????q,?r?=?np.linalg.qr(raw_poly)
????q?*=?np.sign(np.diag(r))
????q?/=?np.sqrt(np.sum(q?**?2,?axis=1))
????q?=?q[:,?1:]
????return?q[order?-?1]

polynomial_encoding?=?ordinal_encoding.apply(lambda?oe:?pd.Series(do_polynomial_encoding(oe)))

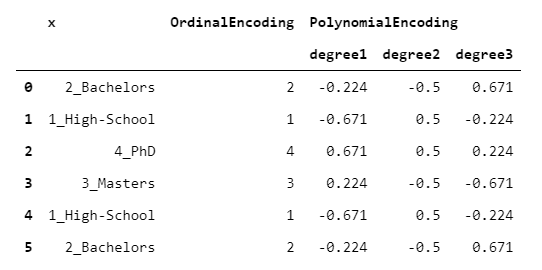
我知道你在想什么。一個(gè)數(shù)值變量如何與一個(gè)非數(shù)值變量有線(xiàn)性（或二次或三次）關(guān)系？這是基于這樣一個(gè)假設(shè)，即潛在的離散變量不僅具有順序性，而且具有等間距。

基于這個(gè)原因，我建議謹(jǐn)慎使用它，只有當(dāng)你確信這個(gè)假設(shè)是合理的。

8.BinaryEncoder

BinaryEncoder 與OrdinalEncoder基本相同，唯一的區(qū)別是將整數(shù)轉(zhuǎn)換成二進(jìn)制數(shù)，然后每個(gè)位置數(shù)字都是one-hot編碼。

binary_base?=?ordinal_encoding.apply(lambda?oe:?str(bin(oe))[2:].zfill(len(bin(len(set(x))))?-?2))
binary_encoding?=?binary_base.apply(lambda?bb:?pd.Series(list(bb))).astype(int)

輸出由偽列組成，就像OneHotEncoder的情況一樣，但是它會(huì)導(dǎo)致相對(duì)于one-hot的維數(shù)降低。

老實(shí)說(shuō)，我不知道這種編碼有什么實(shí)際應(yīng)用。

9.BaseNEncoder

BaseNEncoder只是BinaryEncoder的一個(gè)推廣。實(shí)際上，在BinaryEncoder中，數(shù)字以2為基數(shù)，而在BaseNEncoder中，數(shù)字以n為底，n大于1。

def?int2base(n,?base):
????out?=?''
????while?n:
????????out?+=?str(int(n?%?base))
????????n?//=?base
????return?out[::-1]

base_n?=?ordinal_encoding.apply(lambda?oe:?int2base(n?=?oe,?base?=?base))
base_n_encoding?=?base_n.apply(lambda?bn:?pd.Series(list(bn.zfill(base_n.apply(len).max())))).astype(int)

讓我們看一個(gè)base=3的例子。

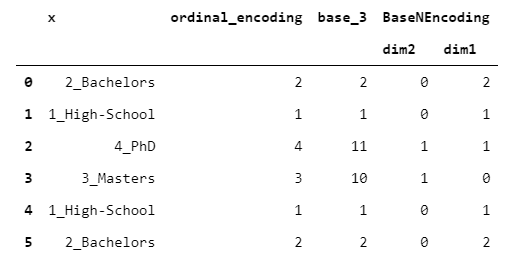
老實(shí)說(shuō)，我不知道這種編碼有什么實(shí)際應(yīng)用。

10.HashingEncoder

在HashingEncoder中，每個(gè)原始級(jí)別都使用一些哈希算法（如SHA-256）進(jìn)行哈希處理。然后，將結(jié)果轉(zhuǎn)換為整數(shù)，并取該整數(shù)相對(duì)于某個(gè)（大）除數(shù)的模。通過(guò)這樣做，我們將每個(gè)原始字符串映射到一個(gè)某個(gè)范圍的整數(shù)。最后，這個(gè)過(guò)程得到的整數(shù)是one-hot編碼的。

def?do_hash(string,?output_dimension):
????hasher?=?hashlib.new('sha256')
????hasher.update(bytes(string,?'utf-8'))
????string_hashed?=?hasher.hexdigest()
????string_hashed_int?=?int(string_hashed,?16)
????string_hashed_int_remainder?=?string_hashed_int?%?output_dimension
????return?string_hashed,?string_hashed_int,?string_hashed_int_remainder

hashing?=?x.apply(
????lambda?string:?pd.Series(do_hash(string,?output_dimension),?
????????index?=?['x_hashed',?'x_hashed_int',?'x_hashed_int_remainder']))
hashing_encoding?=?hashing['x_hashed_int_remainder'].apply(lambda?rem:?pd.Series(np.diag(np.ones(output_dimension))[rem])).astype(int)

讓我們看一個(gè)輸出維數(shù)為10的示例。

散列的基本特性是得到的整數(shù)是均勻分布的。所以，如果除數(shù)足夠大，兩個(gè)不同的字符串不太可能映射到同一個(gè)整數(shù)。那為什么有用呢？實(shí)際上，這有一個(gè)非常實(shí)際的應(yīng)用叫做“哈希技巧”。

假設(shè)你希望使用邏輯回歸來(lái)生成電子郵件垃圾郵件分類(lèi)器。你可以通過(guò)對(duì)數(shù)據(jù)集中包含的所有單詞進(jìn)行ONE-HOT編碼來(lái)實(shí)現(xiàn)這一點(diǎn)。主要的缺點(diǎn)是你需要將映射存儲(chǔ)在單獨(dú)的字典中，并且你的模型維度將在新字符串出現(xiàn)時(shí)發(fā)生更改。

使用散列技巧可以很容易地克服這些問(wèn)題，因?yàn)橥ㄟ^(guò)散列輸入，你不再需要字典，并且輸出維是固定的（它只取決于你最初選擇的除數(shù)）。此外，對(duì)于散列的屬性，你可以認(rèn)為新字符串可能具有與現(xiàn)有字符串不同的編碼。

11.TargetEncoder

假設(shè)有兩個(gè)變量：一個(gè)是離散變量（x），一個(gè)是數(shù)值變量（y）。假設(shè)你想把x轉(zhuǎn)換成一個(gè)數(shù)值變量。你可能需要使用y“攜帶”的信息。一個(gè)明顯的想法是取x的每個(gè)級(jí)別的y的平均值。在公式中：

這是合理的，但是這種方法有一個(gè)很大的問(wèn)題：有些群體可能太小或太不穩(wěn)定而不可靠。許多有監(jiān)督編碼通過(guò)在組平均值和y的全局平均值之間選擇一種中間方法來(lái)克服這個(gè)問(wèn)題：

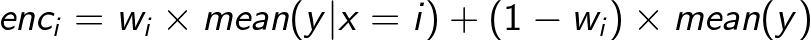
其中$w_i$在0和1之間，取決于組的“可信”程度。

接下來(lái)的三種算法（TargetEncoder、MEstimateEncoder和JamesSteinEncoder）根據(jù)它們定義$w_i$的方式而有所不同。

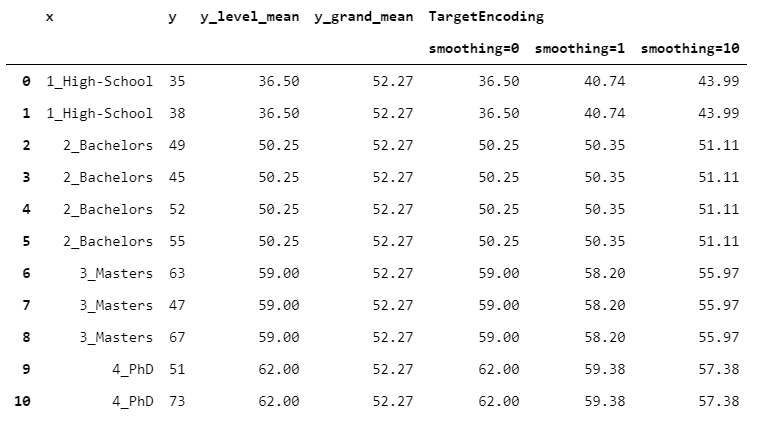
在TargetEncoder中，權(quán)重取決于組的數(shù)量和一個(gè)稱(chēng)為“平滑”的參數(shù)。當(dāng)“平滑”為0時(shí)，我們僅依賴(lài)組平均值。然后，隨著平滑度的增加，全局平均權(quán)值越來(lái)越多，導(dǎo)致正則化更強(qiáng)。

y_mean?=?y.mean()
y_level_mean?=?x.replace(y.groupby(x).mean())
weight?=?1?/?(1?+?np.exp(-(count_encoding?-?1)?/?smoothing))
target_encoding?=?y_level_mean?*?weight?+?y_mean?*?(1?-?weight)

讓我們看看結(jié)果如何隨著一些不同的平滑值而變化。

12.MEstimateEncoder

MEstimateEncoder類(lèi)似于TargetEncoder，但$w_i$取決于一個(gè)名為“m”的參數(shù)，該參數(shù)設(shè)置全局平均值的絕對(duì)權(quán)重。m很容易理解，因?yàn)樗梢员灰暈槿舾蓚€(gè)觀(guān)測(cè)值：如果等級(jí)正好有m個(gè)觀(guān)測(cè)值，那么等級(jí)平均值和總體平均權(quán)重是相同的。

y_mean?=?y.mean()
y_level_mean?=?x.replace(y.groupby(x).mean())
weight?=?count_encoding?/?(count_encoding?+?m)
m_estimate_encoding?=??y_level_mean?*?weight?+?y_grand_mean?*?(1?-?weight)

讓我們看看不同m值的結(jié)果是如何變化的：

13.「JamesSteinEncoder」

TargetEncoder和MEstimateEncoder既取決于組的數(shù)量，也取決于用戶(hù)設(shè)置的參數(shù)值（分別是smoothing和m）。這不方便，因?yàn)樵O(shè)置這些權(quán)重是一項(xiàng)手動(dòng)任務(wù)。

一個(gè)自然的問(wèn)題是：有沒(méi)有一種方法可以在不需要任何人為干預(yù)的情況下，設(shè)定一個(gè)最佳的工作環(huán)境？JamesSteinEncoder試圖以一種基于統(tǒng)計(jì)數(shù)據(jù)的方式來(lái)做到這一點(diǎn)。

y_mean?=?y.mean()
y_var?=?y.var()
y_level_mean?=?x.replace(y.groupby(x).mean())
y_level_var?=?x.replace(y.groupby(x).var())

weight?=?1?-?(y_level_var?/?(y_var?+?y_level_var)?*?(len(set(x))?-?3)?/?(len(set(x))?-?1))
james_stein_encoding?=?y_level_mean?*?weight?+?y_mean?*?(1?-?weight)

直覺(jué)是，一個(gè)高方差的群體的平均值應(yīng)該不那么可信。因此，群體方差越高，權(quán)重就越低（如果你想知道更多關(guān)于公式的知識(shí)，我建議克里斯?賽義德的這篇文章）。

讓我們看一個(gè)數(shù)值示例：

JamesSteinEncoder有兩個(gè)顯著的優(yōu)點(diǎn)：它提供比最大似然估計(jì)更好的估計(jì)，并且不需要任何參數(shù)設(shè)置。

14.GLMMEncoder

GLMMEncoder采用一種完全不同的方法。

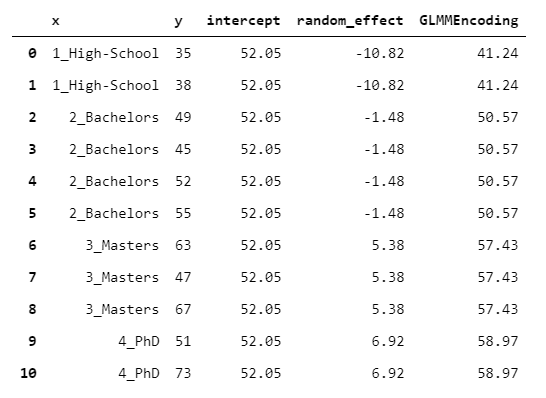
基本上，它擬合y上的線(xiàn)性混合效應(yīng)模型。這種方法利用了一個(gè)事實(shí)，即線(xiàn)性混合效應(yīng)模型是為處理同質(zhì)觀(guān)察組而精心設(shè)計(jì)的。因此，我們的想法是擬合一個(gè)沒(méi)有回歸變量(只有截距)的模型，并使用層次作為組。

然后，輸出就是截距和隨機(jī)效應(yīng)的總和。

model?=?smf.mixedlm(formula?=?'y?~?1',?data?=?y.to_frame(),?groups?=?x).fit()
intercept?=?model.params['Intercept']
random_effect?=?x.replace({k:?float(v)?for?k,?v?in?model.random_effects.items()})
glmm_encoding?=?intercept?+?random_effect

15.WOEEncoder

WOEEncoder（代表“證據(jù)權(quán)重 Weight of Evidence”編碼器）只能用于二元變量，即級(jí)別為0/1的目標(biāo)變量。

證據(jù)權(quán)重背后的想法是你有兩種分布：

• 1的分布（每組1的個(gè)數(shù)/y中1的個(gè)數(shù)）
• 0的分布（每組0的個(gè)數(shù)/y中0的個(gè)數(shù)）

該算法的核心是將1的分布除以0的分布(對(duì)于每個(gè)組)。當(dāng)然，這個(gè)值越高，我們就越有信心認(rèn)為這個(gè)基團(tuán)“偏向”1，反之亦然。然后，取該值的對(duì)數(shù)。

y_level_ones?=?x.replace(y.groupby(x).apply(lambda?l:?(l?==?1).sum()))
y_level_zeros?=?x.replace(y.groupby(x).apply(lambda?l:?(l?==?0).sum()))
y_ones?=?(y?==?1).sum()
y_zeros?=?(y?==?0).sum()
nominator?=?y_level_ones?/?y_ones
denominator?=?y_level_zeros?/?y_zeros
woe_encoder?=?np.log(nominator?/?denominator)

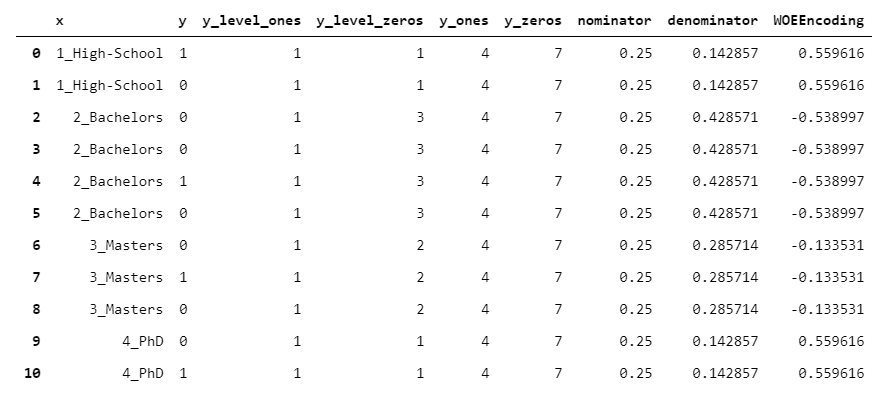
如你所見(jiàn)，由于公式中存在對(duì)數(shù)，因此無(wú)法直接解釋輸出。然而，它作為機(jī)器學(xué)習(xí)的一個(gè)預(yù)處理步驟工作得很好。

16.LeaveOneOutEncoder

到目前為止，所有的15個(gè)編碼器都有一個(gè)唯一的映射。

但是，如果你計(jì)劃使用編碼作為預(yù)測(cè)模型的輸入（例如GB），這可能是一個(gè)問(wèn)題。實(shí)際上，假設(shè)你使用TargetEncoder。這意味著你在X_train中引入了關(guān)于y_train的信息，這可能會(huì)導(dǎo)致嚴(yán)重的過(guò)擬合風(fēng)險(xiǎn)。

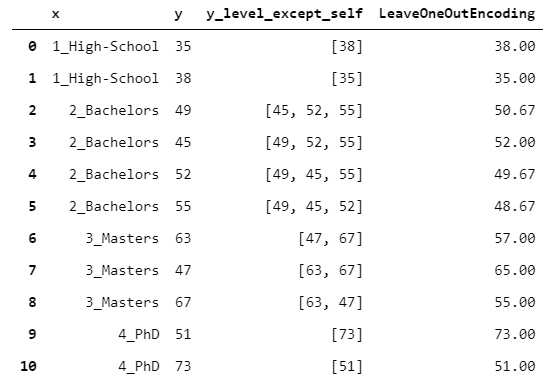
關(guān)鍵是：如何在限制過(guò)擬合的風(fēng)險(xiǎn)的同時(shí)保持有監(jiān)督的編碼？LeaveOneOutEncoder提供了一個(gè)出色的解決方案。它執(zhí)行普通的目標(biāo)編碼，但是對(duì)于每一行，它不考慮該行觀(guān)察到的y值。這樣，就避免了行方向的泄漏。

y_level_except_self?=?x.to_frame().apply(lambda?row:?y[x?==?row['x']].drop(row.name).to_list(),?axis?=?1)
leave_one_out_encoding?=?y_level_except_self.apply(np.mean)

17.CatBoostEncoder

CatBoost是一種梯度提升算法（如XGBoost或LightGBM），它在許多問(wèn)題中都表現(xiàn)得非常好。

CatboostEncoder的工作原理基本上類(lèi)似于LeaveOneOutEncoder，但是是一個(gè)在線(xiàn)方法。

但是如何模擬在線(xiàn)行為？想象一下你有一張桌子。然后，在桌子中間的某個(gè)地方劃一排。CatBoost所做的是假裝當(dāng)前行上方的行已經(jīng)被及時(shí)觀(guān)察到，而下面的行還沒(méi)有被觀(guān)察到（即將來(lái)會(huì)觀(guān)察到）。然后，該算法執(zhí)行l(wèi)eave one out編碼，但僅基于已觀(guān)察到的行。

y_mean?=?y.mean()
y_level_before_self?=?x.to_frame().apply(lambda?row:?y[(x?==?row['x'])?&?(y.index?1)
catboost_encoding?=?y_level_before_self.apply(lambda?ylbs:?(sum(ylbs)?+?y_mean?*?a)?/?(len(ylbs)?+?a))

這似乎有些荒謬。為什么要拋棄一些可能有用的信息呢?你可以將其簡(jiǎn)單地視為對(duì)輸出進(jìn)行隨機(jī)化的更極端嘗試(例如，減少過(guò)擬合)。

謝謝你的閱讀！我希望你覺(jué)得這篇文章有用。