用 Java 實(shí)現(xiàn)常見的 8 種內(nèi)部排序算法
點(diǎn)擊上方藍(lán)色字體,選擇“標(biāo)星公眾號(hào)”
優(yōu)質(zhì)文章,第一時(shí)間送達(dá)
一、插入類排序
插入類排序就是在一個(gè)有序的序列中,插入一個(gè)新的關(guān)鍵字。從而達(dá)到新的有序序列。插入排序一般有直接插入排序、折半插入排序和希爾排序。
1. 插入排序
1.1 直接插入排序
/**
* 直接比較,將大元素向后移來移動(dòng)數(shù)組
*/
public static void InsertSort(int[] A) {
for(int i = 1; i < A.length; i++) {
int temp = A[i]; //temp 用于存儲(chǔ)元素,防止后面移動(dòng)數(shù)組被前一個(gè)元素覆蓋
int j;
for(j = i; j > 0 && temp < A[j-1]; j--) { //如果 temp 比前一個(gè)元素小,則移動(dòng)數(shù)組
A[j] = A[j-1];
}
A[j] = temp; //如果 temp 比前一個(gè)元素大,遍歷下一個(gè)元素
}
}
/**
* 這里是通過類似于冒泡交換的方式來找到插入元素的最佳位置。而傳統(tǒng)的是直接比較,移動(dòng)數(shù)組元素并最后找到合適的位置
*/
public static void InsertSort2(int[] A) { //A[] 是給定的待排數(shù)組
for(int i = 0; i < A.length - 1; i++) { //遍歷數(shù)組
for(int j = i + 1; j > 0; j--) { //在有序的序列中插入新的關(guān)鍵字
if(A[j] < A[j-1]) { //這里直接使用交換來移動(dòng)元素
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
}
}
}
}
/**
* 時(shí)間復(fù)雜度:兩個(gè) for 循環(huán) O(n^2)
* 空間復(fù)雜度:占用一個(gè)數(shù)組大小,屬于常量,所以是 O(1)
*/
1.2 折半插入排序
/*
* 從直接插入排序的主要流程是:1.遍歷數(shù)組確定新關(guān)鍵字 2.在有序序列中尋找插入關(guān)鍵字的位置
* 考慮到數(shù)組線性表的特性,采用二分法可以快速尋找到插入關(guān)鍵字的位置,提高整體排序時(shí)間
*/
public static void BInsertSort(int[] A) {
for(int i = 1; i < A.length; i++) {
int temp = A[i];
//二分法查找
int low = 0;
int high = i - 1;
int mid;
while(low <= high) {
mid = (high + low)/2;
if (A[mid] > temp) {
high = mid - 1;
} else {
low = mid + 1;
}
}
//向后移動(dòng)插入關(guān)鍵字位置后的元素
for(int j = i - 1; j >= high + 1; j--) {
A[j + 1] = A[j];
}
//將元素插入到尋找到的位置
A[high + 1] = temp;
}
}
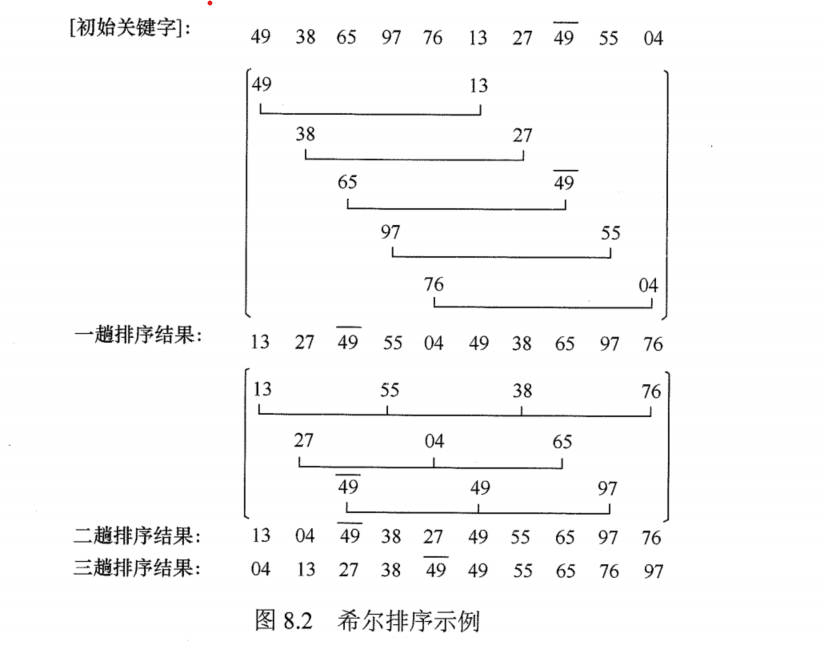
2. 希爾排序
希爾排序又稱縮小增量排序,其本質(zhì)還是插入排序,只不過是將待排序列按某種規(guī)則分成幾個(gè)子序列,然后如同前面的插入排序一般對(duì)這些子序列進(jìn)行排序。因此當(dāng)增量為 1 時(shí),希爾排序就是插入排序,所以希爾排序最重要的就是增量的選取。
主要步驟是:
將待排序數(shù)組按照初始增量 d 進(jìn)行分組
在每個(gè)組中對(duì)元素進(jìn)行直接插入排序
將增量 d 折半,循環(huán) 1、2 、3步驟
待 d = 1 時(shí),最后一次使用直接插入排序完成排序
/**
* 希爾排序的實(shí)現(xiàn)代碼還是比較簡潔的,除了增量的變化,基本上和直接插入序列沒有區(qū)別
*/
public static void ShellSort(int[] A) {
for(int d = A.length/2; d >= 1; d = d/2) { //增量的變化,從 d = "數(shù)組長度一半"到 d = 1
for(int i = d; i < A.length; i++) { //在一個(gè)增量范圍內(nèi)進(jìn)行遍歷[d,A.length-1]
if(A[i] < A[i - d]) { //若增量后的元素小于增量前的元素,進(jìn)行插入排序
int temp = A[i];
int j;
for(j = i - d; j >= 0 && temp < A[j-d]; j -= d) { //對(duì)該增量序列下的元素進(jìn)行排序
A[j + d] = A[j]; //這里要使用i + d 的方式來移動(dòng)元素,因?yàn)樵隽?nbsp;d 可能大于數(shù)組下標(biāo)
} //造成數(shù)組序列超出數(shù)組的范圍
A[j + d] = temp;
}
}
}
}
復(fù)雜度分析
| 排序方法 | 空間復(fù)雜度 | 最好情況 | 最壞情況 | 平均時(shí)間復(fù)雜度 |
|---|---|---|---|---|
| 直接插入排序 | O(1) | O(n^2) | O(n^2) | O(n^2) |
| 折半插入排序 | O(1) | O(nlog2n) | O(n^2) | O(n^2) |
| 希爾排序 | O(1) | O(nlog2n) | O(nlog2n) | O(nlog2n) |
二、交換類排序
交換,指比較兩個(gè)元素關(guān)鍵字大小,來交換兩個(gè)元素在序列中的位置,最后達(dá)到整個(gè)序列有序的狀態(tài)。主要有冒泡排序和快速排序
3. 冒泡排序
冒泡排序就是通過依次比較序列中兩個(gè)相鄰元素的值,根據(jù)需要的升降序來交換這兩個(gè)元素。最終達(dá)到整個(gè)序列有序的結(jié)果。
/**
* 冒泡排序
*/
public static void BubbleSort(int[] A) {
for (int i = 0; i < A.length - 1; i++) { //冒泡次數(shù),遍歷數(shù)組次數(shù),有序元素個(gè)數(shù)
for(int j = 0; j < A.length - i - 1; j++) { //對(duì)剩下無序元素進(jìn)行交換排序
if(A[j] > A[j + 1]) {
int temp = A[j];
A[j] = A[j + 1];
A[j + 1] = temp;
}
}
}
}
4. 快速排序
快速排序?qū)嶋H上也是屬于交換類的排序,只是它通過多次劃分操作實(shí)現(xiàn)排序。這就是分治思想,把一個(gè)序列分成兩個(gè)子序列它每一趟選擇序列中的一個(gè)關(guān)鍵字作為樞軸,將序列中比樞軸小的移到前面,大的移到后邊。當(dāng)本趟所有子序列都被樞軸劃分完畢后得到一組更短的子序列,成為下一趟劃分的初始序列集。每一趟結(jié)束后都會(huì)有一個(gè)關(guān)鍵字達(dá)到最終位置。
/**
* 快速排序算是在冒泡排序的基礎(chǔ)上的遞歸分治交換排序
* @param A 待排數(shù)組
* @param low 數(shù)組起點(diǎn)
* @param high 數(shù)組終點(diǎn)
*/
public static void QuickSort(int[] A, int low, int high) {
if(low >= high) { //遞歸分治完成退出
return;
}
int left = low; //設(shè)置左遍歷指針 left
int right = high; //設(shè)置右遍歷指針 right
int pivot = A[left]; //設(shè)置樞軸 pivot, 默認(rèn)是數(shù)組最左端的值
while(left < right) { //循環(huán)條件
while(left < right && A[right] >= pivot) {//若右指針?biāo)赶蛟卮笥跇休S值,則右指針向左移動(dòng)
right--;
}
A[left] = A[right]; //反之替換
while (left < right && A[left] <= pivot) {//若左指針?biāo)赶蛟匦∮跇休S值,則左指針向右移動(dòng)
left++;
}
A[right] = A[left]; //反之替換
}
A[left] = pivot; //將樞軸值放在最終位置上
QuickSort(A, low, left - 1); //依此遞歸樞軸值左側(cè)的元素
QuickSort(A, left + 1, high); //依此遞歸樞軸值右側(cè)的元素
}
復(fù)雜度分析
| 排序方法 | 空間復(fù)雜度 | 最好情況 | 最壞情況 | 平均時(shí)間復(fù)雜度 |
|---|---|---|---|---|
| 冒泡排序 | O(1) | O(n^2) | O(n^2) | O(n^2) |
| 快速排序 | O(log2n) | O(nlog2n) | O(n^2) | O(nlog2n) |
三、選擇排序
選擇排序就是每一趟從待排序列中選擇關(guān)鍵字最小的元素,直到待排序列元素選擇完畢。
5. 簡單選擇排序
/**
* 簡單選擇排序
* @param A 待排數(shù)組
*/
public static void SelectSort(int [] A) {
for (int i = 0; i < A.length; i++) {
int min = i; //遍歷選擇序列中的最小值下標(biāo)
for (int j = i + 1; j < A.length; j++) { //遍歷當(dāng)前序列選擇最小值
if (A[j] < A[min]) {
min = j;
}
}
if (min != i) { //選擇并交換最小值
int temp = A[min];
A[min] = A[i];
A[i] = temp;
}
}
}
6.堆排序
堆是一種數(shù)據(jù)結(jié)構(gòu),可以把堆看成一顆完全二叉樹,而且這棵樹任何一個(gè)非葉結(jié)點(diǎn)的值都不大于(或不小于)其左右孩子結(jié)點(diǎn)的值。若父結(jié)點(diǎn)大子結(jié)點(diǎn)小,則這樣的堆叫做大頂堆;若父結(jié)點(diǎn)小子結(jié)點(diǎn)大,則這樣的堆叫做小頂堆。
堆排序的過程實(shí)際上就是將堆排序的序列構(gòu)造成一個(gè)堆,將堆中最大的取走,再將剩余的元素調(diào)整成堆,然后再找出最大的取走。這樣重復(fù)直至取出的序列有序。
排序主要步驟可以分為(以大頂堆為例):
(1) 將待排序列構(gòu)造成一個(gè)大頂堆:BuildMaxHeap()
(2) 對(duì)堆進(jìn)行調(diào)整排序:AdjustMaxHeap()
(3) 進(jìn)行堆排序,移除根結(jié)點(diǎn),調(diào)整堆排序:HeapSort()
/**
* 堆排序(大頂堆)
* @param A 待排數(shù)組
*/
public static void HeapSort(int [] A) {
BuildMaxHeap(A); //建立堆
for (int i = A.length - 1; i > 0; i--) { //排序次數(shù),需要len - l 趟
int temp = A[i]; //將堆頂元素(A[0])與數(shù)組末尾元素替換,更新待排數(shù)組長度
A[i] = A[0];
A[0] = temp;
AdjustMaxHeap(A, 0, i); //調(diào)整新堆,對(duì)未排序數(shù)組再次進(jìn)行調(diào)整
}
}
/**
* 建立大頂堆
* @param A 待排數(shù)組
*/
public static void BuildMaxHeap(int [] A) {
for (int i = (A.length / 2) -1; i >= 0 ; i--) { //對(duì)[0,len/2]區(qū)間中的的結(jié)點(diǎn)(非葉結(jié)點(diǎn))從下到上進(jìn)行篩選調(diào)整
AdjustMaxHeap(A, i, A.length);
}
}
/**
* 調(diào)整大頂堆
* @param A 待排數(shù)組
* @param k 當(dāng)前大頂堆根結(jié)點(diǎn)在數(shù)組中的下標(biāo)
* @param len 當(dāng)前待排數(shù)組長度
*/
public static void AdjustMaxHeap(int [] A, int k, int len) {
int temp = A[k];
for (int i = 2*k + 1; i < len; i = 2*i + 1) { //從最后一個(gè)葉結(jié)點(diǎn)開始從下到上進(jìn)行堆調(diào)整
if (i + 1 < len && A[i] < A[i + 1]) { //比較兩個(gè)子結(jié)點(diǎn)大小,取其大值
i++;
}
if (temp < A[i]) { //若結(jié)點(diǎn)大于父結(jié)點(diǎn),將父結(jié)點(diǎn)替換
A[k] = A[i]; //更新數(shù)組下標(biāo),繼續(xù)向上進(jìn)行堆調(diào)整
k = i;
} else {
break; //若該結(jié)點(diǎn)小于父結(jié)點(diǎn),則跳過繼續(xù)向上進(jìn)行堆調(diào)整
}
}
A[k] = temp; //將結(jié)點(diǎn)放入比較后應(yīng)該放的位置
}
復(fù)雜度分析
| 排序方法 | 空間復(fù)雜度 | 最好情況 | 最壞情況 | 平均時(shí)間復(fù)雜度 |
|---|---|---|---|---|
| 簡單選擇排序 | O(1) | O(n^2) | O(n^2) | O(n^2) |
| 堆排序 | O(1) | O(log2n) | O(nlog2n) | O(nlog2n) |
四、其他內(nèi)部排序
7. 歸并排序
歸并排序是將多個(gè)有序表組合成一個(gè)新的有序表,該算法是采用分治法的一個(gè)典型的應(yīng)用。即把待排序列分為若干個(gè)子序列,每個(gè)子序列是有序的。然后再把有序子序列合并為一個(gè)整體有序的序列。這里主要以二路歸并排序來進(jìn)行分析。
該排序主要分為兩步:
分解:將序列每次折半拆分
合并:將劃分后的序列兩兩排序并合并
private static int[] aux;
/**
* 初始化輔助數(shù)組 aux
* @param A 待排數(shù)組
*/
public static void MergeSort(int [] A) {
aux = new int[A.length];
MergeSort(A,0,A.length-1);
}
/**
* 將數(shù)組分成兩部分,以數(shù)組中間下標(biāo) mid 分為兩部分依此遞歸
* 最后再將兩部分的有序序列通過 Merge() 函數(shù) 合并
* @param A 待排數(shù)組
* @param low 數(shù)組起始下標(biāo)
* @param high 數(shù)組末尾下標(biāo)
*/
public static void MergeSort (int[] A, int low, int high) {
if (low < high) {
int mid = (low + high) / 2;
MergeSort(A, low, mid);
MergeSort(A, mid + 1, high);
Merge(A, low, mid, high);
}
}
/**
* 將 [low, mid] 有序序列和 [mid+1, high] 有序序列合并
* @param A 待排數(shù)組
* @param low 數(shù)組起始下標(biāo)
* @param mid 數(shù)組中間分隔下標(biāo)
* @param high 數(shù)組末尾下標(biāo)
*/
public static void Merge (int[] A, int low, int mid, int high) {
int i, j, k;
for (int t = low; t <= high; t++) {
aux[t] = A[t];
}
for ( i = low, j = mid + 1, k = low; i <= mid && j <= high; k++) {
if(aux[i] < aux[j]) {
A[k] = aux[i++];
} else {
A[k] = aux[j++];
}
}
while (i <= mid) {
A[k++] = aux[i++];
}
while (j <= high) {
A[k++] = aux[j++];
}
}
8. 基數(shù)排序
基數(shù)排序比較特別,它是通過關(guān)鍵字?jǐn)?shù)字各位的大小來進(jìn)行排序。它是一種借助多關(guān)鍵字排序的思想來對(duì)單邏輯關(guān)鍵字進(jìn)行排序的方法。
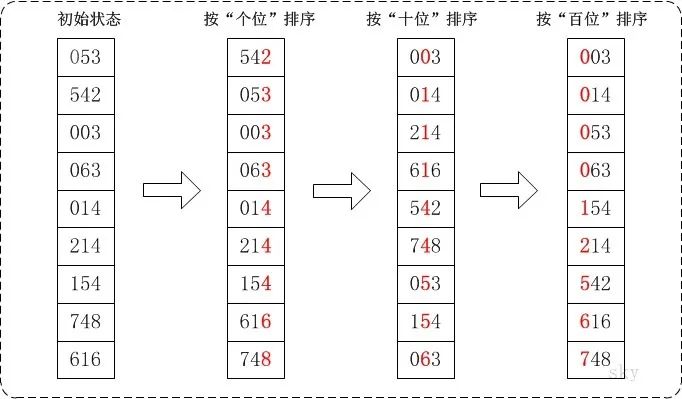
它主要有兩種排序方法:
最高位優(yōu)先法(MSD):按照關(guān)鍵字位權(quán)重高低依此遞減來劃分子序列
最低位優(yōu)先法(LSD) :按照關(guān)鍵字位權(quán)重低高依此增加來劃分子序列
基數(shù)排序的思想:
分配
回收
/**
* 找出數(shù)組中的最長位數(shù)
* @param A 待排數(shù)組
* @return MaxDigit 最長位數(shù)
*/
public static int MaxDigit (int [] A) {
if (A == null) {
return 0;
}
int Max = 0;
for (int i = 0; i < A.length; i++) {
if (Max < A[i]) {
Max = A[i];
}
}
int MaxDigit = 0;
while (Max > 0) {
MaxDigit++;
Max /= 10;
}
return MaxDigit;
}
/**
* 將基數(shù)排序的操作內(nèi)化在一個(gè)二維數(shù)組中進(jìn)行
* @param A 待排數(shù)組
*/
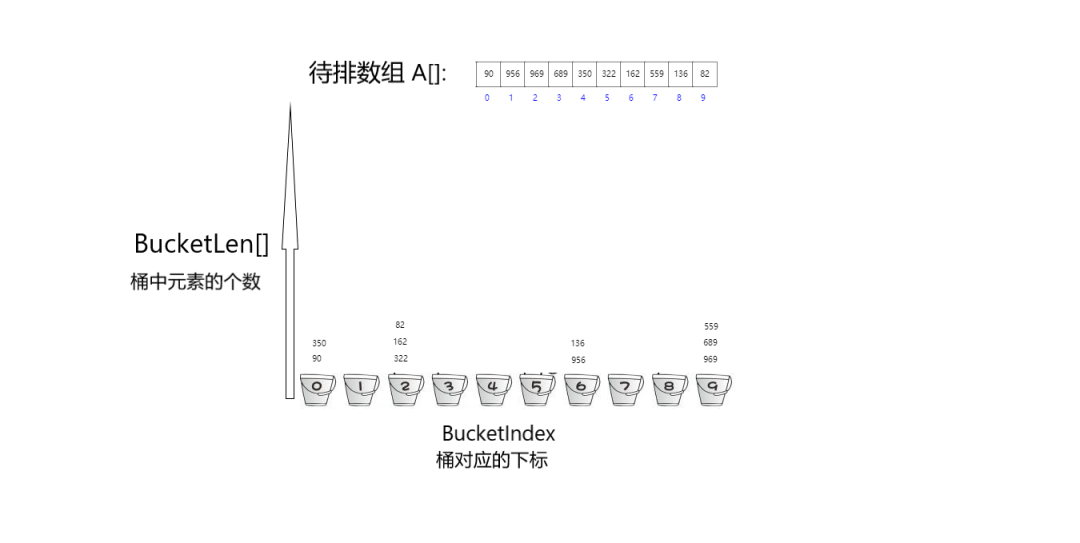
public static void RadixSort(int [] A) {
//創(chuàng)建一個(gè)二維數(shù)組,類比于在直角坐標(biāo)系中,進(jìn)行分配收集操作
int[][] buckets = new int[10][A.length];
int MaxDigit = MaxDigit(A);
//t 用于提取關(guān)鍵字的位數(shù)
int t = 10;
//按排序趟數(shù)進(jìn)行循環(huán)
for (int i = 0; i < MaxDigit; i++) {
//在一個(gè)桶中存放元素的數(shù)量,是buckets 二維數(shù)組的y軸
int[] BucketLen = new int[10];
//分配操作:將待排數(shù)組中的元素依此放入桶中
for (int j = 0; j < A.length ; j++) {
//桶的下標(biāo)值,是buckets 二維數(shù)組的x軸
int BucketIndex = (A[j] % t) / (t / 10);
buckets[BucketIndex][BucketLen[BucketIndex]] = A[j];
//該下標(biāo)下,也就是桶中元素個(gè)數(shù)隨之增加
BucketLen[BucketIndex]++;
}
//收集操作:將已排好序的元素從桶中取出來
int k = 0;
for (int x = 0; x < 10; x++) {
for (int y = 0; y < BucketLen[x]; y++) {
A[k++] = buckets[x][y];
}
}
t *= 10;
}
}
復(fù)雜度分析
| 排序方法 | 空間復(fù)雜度 | 最好情況 | 最壞情況 | 平均時(shí)間復(fù)雜度 |
|---|---|---|---|---|
| 歸并排序 | O(n) | O(nlog2n) | O(nlog2n) | O(nlog2n) |
| 基數(shù)排序 | O(rd) | O(d(n+rd)) | O(d(n+rd)) | O(d(n+rd)) |
備注:基數(shù)排序中,n 為序列中的關(guān)鍵字?jǐn)?shù),d為關(guān)鍵字的關(guān)鍵字位數(shù),rd 為關(guān)鍵字位數(shù)的個(gè)數(shù)
作者 | Ethan_Wong
來源 | cnblogs.com/EthanWong/p/15130587.html

