保姆級教學!徹底學會時間復雜度和空間復雜度
大家好呀,我是蛋蛋。
數(shù)據結構與算法,作為編程界從入門到勸退的王者,是很多初學者心中神圣而想侵犯的村花兒,化身舔狗,費盡心思,舔到最后,我命油我不油天。

作為一名大學之前編程能力為零,以為計算機專業(yè)就是打游戲的咸魚,到參加 ACM 競賽,靠著劃水和抱大腿拿了幾塊金銀銅鐵牌的前 ACM 混子選手,想起之前瘋狂跪舔數(shù)據結構和算法的日子,至今我扔能掬出一把辛酸淚。

為了讓臭寶們不再像我這樣當個人這么難,我決定和大家一起學習數(shù)據結構與算法,我希望能用傻瓜的方式,由淺入深,從概念到實踐,一步一步的來,這個過程可能會很長,我希望在這個過程中你能喜歡上它,能發(fā)現(xiàn)它們冰冷外表下有趣的靈魂。
學習數(shù)據結構與算法的第一課,我永遠都選復雜度分析,在我看來,這是數(shù)據結構與算法中最重要的知識點,且不接受任何反駁。

復雜度分析主要就是時間復雜度和空間復雜度,接下來的文章也主要圍繞這兩方面來講。廢話不多說,前排馬扎瓜子準備好,蛋蛋小課堂正式接客
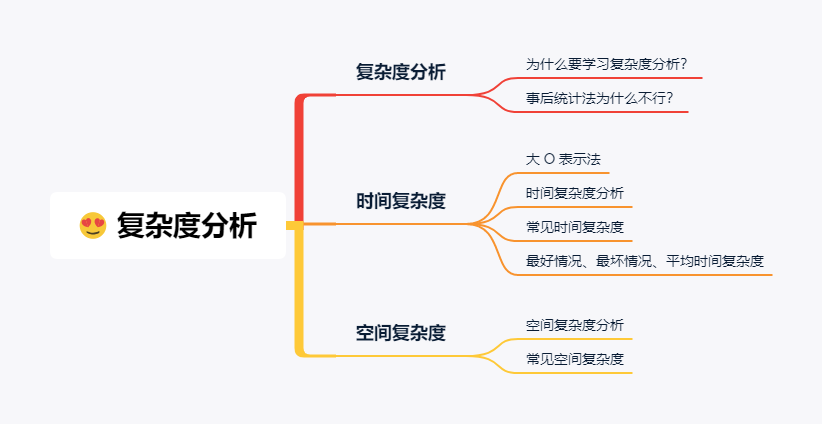
復雜度分析
剛剛我說過,在本蛋看來,復雜度分析是數(shù)據結構和算法中最重要的知識點,毫不夸張的說,這就是數(shù)據結構與算法學習的核心所在。你學會了它你就入的了門,你學不會它,你就永遠不知道門兒在哪。
為什么復雜度分析會這么重要?
這個就要從盤古開天辟地,呃,從數(shù)據結構與算法的本身說起。
我平常白天做夢的時候,總是想著當當咸魚劃劃水就能賺大錢,最好就是能躺著,錢就直接砸到我腦闊上。數(shù)據結構與算法雖然沒有本蛋這么大的夢想,但是它的出現(xiàn)也是想著花更少的時間和更少的存儲來解決問題。
那如何去考量“更少的時間和更少的存儲”,復雜度分析為此而生。

既然你誠心誠意的不知道,那我就大發(fā)慈悲的打個不恰當?shù)谋确健?/span>
如果把數(shù)據結構與算法看成武功招式,那復雜度分析就是對應的心法。
如果只是學會了數(shù)據結構與算法的用法,不學復雜度分析,這就和你費盡千辛萬苦在隔壁老王家次臥進門右手第二塊地磚下偷挖出老王打遍村里無敵手的村林至寶王霸拳,然后發(fā)現(xiàn)秘籍上只有招式,沒有內功心法,好好得王霸拳變的還不如王八拳。只有學會了王霸之氣,才能虎軀一震,王霸之氣一噗,震走村口光棍李養(yǎng)的哈巴狗。

吐樣吐森破!吃葡萄不吐葡萄皮!
你們說的這種主流叫做事后統(tǒng)計法。
簡單來說,就是你需要提前寫好算法代碼和編好測試數(shù)據,然后在計算機上跑,通過最后得出的運行時間判斷算法時效的高低,這里的運行時間就是我們日常的時間。
我且不用“萬一你費勁心思寫好的算法代碼本身是個很糟糕的解法”這種理由去反駁你,事后統(tǒng)計法本身存在很多缺陷,它并不是一個對我們來說有用的度量指標:
首先,事后統(tǒng)計法太依賴計算機的軟件和硬件等性能。代碼在 core i7 處理器的就比 core i5 處理器的運算速度快,更不用說不同的操作系統(tǒng)、不同的編程語言等軟件方面,就算是在同一臺電腦上,用的所有的東西都一樣,內存的占用或者是 CPU 的使用率也會造成運行時間的差異。
再者,事后統(tǒng)計法太依賴于測試數(shù)據集的規(guī)模。同樣是排序算法,你隨便整 5 個 10 個的數(shù)排序,就算最垃圾的排序算法,也看起來快的和法拉利一樣,如果是來10w 個 100w 個,那不同的算法的差距就很大了,而且同樣是 10w 個 100w 個數(shù),順序和亂序的時間又不同了。
那么問題來了,到底測試數(shù)據集選多少個合適?數(shù)據的順序如何定又算合適?
說不出來了叭?

可以看出,我們需要一個不依賴于性能和規(guī)模等外力影響就可以估算算法效率、判斷算法優(yōu)劣的度量指標,而復雜度分析天生就是干這個的,這也是為什么我們要學習并必須學會復雜度分析!
時間復雜度
時間復雜度,也就是指算法的運行時間。
對于某一問題的不同解決算法,運行時間越短算法效率越高,相反,運行時間越長,算法效率越低。
那么如何估算時間復雜度呢?
大佬們在拽掉腦闊上最后一根頭發(fā)的時候發(fā)現(xiàn),當用運行時間去描述一個算法快慢的時候,算法中執(zhí)行的總步數(shù)顯得尤為重要。
因為只是估算,我們可以假設每一行代碼的運行時間都為一個 Btime,那么算法的總的運行時間 = 運行的總代碼行數(shù)。
下面我們來看這么一段簡單的代碼。
def dogeggs_sum (n):sum = 0for dogegg in range(n):sum += dogeggreturn sum
在上面假設的情況下,這段求累加和的代碼總的運行時間是多少呢?
第 2 行代碼需要 1 Btime 的運行時間,第 4 和 第 5行分別運行了 n 次,所以每個需要 n * Btime 的運行時間,所以總的運行時間就是 (1 + 2n) * Btime。
我們一般用 T 函數(shù)來表示賦值語句的總運行時間,所以上面總的運行時間就可以表達成 T(n) = (1 + 2n) * Btime,翻譯一下就是“數(shù)據集大小為 n,總步數(shù)為 (1 + 2n) 的算法的執(zhí)行時間為 T(n)”。
通過公式,我們可以看出 T(n) 和總步數(shù)是成正比關系,這個規(guī)律的發(fā)現(xiàn)其實是很重要的,因為這個告訴了我們一種趨勢,數(shù)據集規(guī)模和運行時間之間有趨勢!
所有人準備,我們很熟悉的大 O 閃亮登場了!

大 O 表示法
大 O 表示法,表示的是算法有多快。
這個多快,不是說算法代碼真正的運行時間,而是代表著一種趨勢,一種隨著數(shù)據集的規(guī)模增大,算法代碼運行時間變化的一種趨勢。一般記作 O(f(n))。
那么之前的公式就變成 T(n) = O(f(n)),其中 f(n) 是算法代碼執(zhí)行的總步數(shù),也叫操作數(shù)。
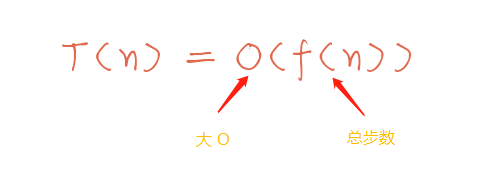
n 作為數(shù)據集大小,它可以取 1,10,100,1000 或者更大更大更大的數(shù),到這你就會發(fā)現(xiàn)一件很有意思的事兒,那就是當數(shù)據集越來越大時,你會發(fā)現(xiàn)代碼中的某些部分“失效”了。
還是以之前的代碼為例。當 n = 1000 時,1 + 2n = 2001,當 n = 10000 時,1 + 2n = 20001,當這個 n 持續(xù)增大時,常數(shù) 1 和系數(shù) 2 對于最后的結果越來越沒存在感,即對趨勢的變化影響不大。
所以對于我們這段代碼樣例,最終的 T(n) = O(n)。
接下來再用兩段代碼進一步學一下求時間復雜度分析。
時間復雜度分析
代碼 1
def dogeggs_sum (n):sum = 0for dogegg in range(n):for i in range(n):sum += dogegg * ireturn sum
這段代碼我會從最開始一點點帶你來。
第 2 行需要運行 1 次 ,第 4 行需要運行 n 次,第 5 行和第 6 行分別需要運行 n2 次。所以總的運行次數(shù) f(n) = 1 + n + 2n2。
當 n 為 5 的時候,f(n) = 1 + 5 + 2 * 25,當 n 為 10000 的時候,f(n) = 1 + 10000 + 2 * 100000000,當 n 更大呢?
這個時候其實很明顯的就可以看出來 n2 起到了決定性的作用,像常數(shù) 1,一階 n 和 系數(shù) 2 對最終的結果(即趨勢)影響不大,所以我們可以把它們直接忽略掉,所以執(zhí)行的總步數(shù)就可以看成是“主導”結果的那個,也就是 f(n) = n2。
自然代碼的運行時間 T(n) = O(f(n)) = O(n2)。
代碼 2
def dogeggs_sum (n):sum1 = 0for dogegg1 in range(n):sum1 += dogegg1sum2 = 0for dogegg2 in range(n):for i in range(n):sum2 += dogegg2 * isum3 = 0for dogegg3 in range(n):for i in range(n):for j in range(n):sum3 += dogegg3 * i * jreturn sum1 + sum2 + sum3
上面這段代碼是求三部分的和,經過之前的學習應該很容易知道,第一部分的時間復雜度是 O(n),第二部分的時間復雜度是 O(n2),第三部分是 O(n3)。
正常來講,這段代碼的 T(n) = O(n) + O(n2) + O(n3),按照我們取“主導”部分,顯然前面兩個小弟都應該直接 pass,最終 T(n) = O(n3)。
通過這幾個例子,聰明的小婊貝們肯定會發(fā)現(xiàn),對于時間復雜度分析來說,只要找起“主導”作用的部分代碼即可,這個主導就是最高的那個復雜度,也就是執(zhí)行次數(shù)最多的那部分 n 的量級。
剩下的就是多加練習,有意識的多去想多去練,就可以和我一樣 帥氣 穩(wěn)啦。

常見時間復雜度
算法學習過程中,我們會遇到各種各樣的時間復雜度,但縱使你代碼七十二變,幾乎也逃不過下面這幾種常見的時間復雜度。
| 時間復雜度 | 階 | f(n) 舉例 |
| 常數(shù)復雜度 | O(1) | 1 |
| 對數(shù)復雜度 | O(logn) | logn + 1 |
| 線性復雜度 | O(n) | n + 1 |
| 線性對數(shù)復雜度 | O(nlogn) | nlogn + 1 |
| k 次復雜度 | O(n2)、O(n3)、.... | n2 + n +1 |
| 指數(shù)復雜度 | O(2n) | 2n + 1 |
| 階乘復雜度 | O(n!) | n! + 1 |
上表的時間復雜度由上往下依次增加,O(n) 和 O(n2) 前面已經講過了,O(2n) 和 O(n!) 效率低到離譜,以后不幸碰到我再提一下,就不再贅述。
下面主要來看剩下幾種最常見的時間復雜度。
O(1)
O(1) 是常數(shù)時間復雜度。
在這你要先明白一個概念,不是只執(zhí)行 1 次的代碼的時間復雜度記為 O(1),只要你是常數(shù),像 O(2)、O(3) ... O(100000) 在復雜度的表示上都是 O(1)。
n = 10000res = n / 2print(res)
比如像上面這段代碼,它運行了 3 次,但是它的時間復雜度記為 O(1),而不是 O(3)。
因為無論 n 等于多少,對于它們每行代碼來說還是只是執(zhí)行了一次,代碼的執(zhí)行時間不隨 n 的變化而變化。
O(logn)
O(logn) 是對數(shù)時間復雜度。首先我們來看一段代碼:
dogegg = 1while dogegg < n:dogegg = dogegg * 2
根據之前講的,我們先找“主導”,在這主導就是第 4 行代碼,只要算出它的時間復雜度,總的時間復雜度就知道了。
其實很簡單,上面的代碼翻譯一下就是初始化 dogegg = 1, 乘上多少個 2 以后會 ≥ n。

假設需要 x 個,那么相當于求:
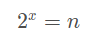
即:
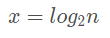
所以上述代碼的時間復雜度應該為 O(log2n)。
但是對于對數(shù)復雜度來說,不管你是以 2、3 為底,還是以 10 為底,通通記作 O(logn),這是為什么呢?
這就要從對數(shù)的換底公式說起。
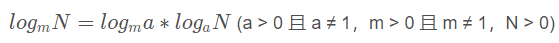
根據換底公式,log2n 可以寫成:
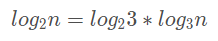
對于時間復雜度來說:
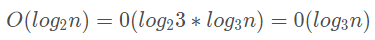
所以在對數(shù)時間復雜度中我們就忽略了底,直接用 O(logn) 來表示對數(shù)時間復雜度。
O(nlogn)
O(nlogn),真的是很常見的時間復雜度,像后面會學到的快速排序、歸并排序的時間復雜度都是 O(nlogn)。
如果只是簡單看的話是在 logn 外面套了層 for 循環(huán),比如像下面這段代碼:
def stupid_cnt(n):cnt = 0for i in range(n):dogegg = 1while dogegg < n:dogegg = dogegg * 2cnt += 1return cnt
當然像上面這種 stupid 代碼一般人不會寫,我也只是舉個例子給大家看,我是狗蛋,大家千萬不要以為我是傻狗。

最好情況、最壞情況和平均情況時間復雜度
除了數(shù)據集規(guī)模影響算法的運行時間外,“數(shù)據的具體情況”也會影響到運行時間。
我們來看這么一段代碼:
def find_word(lst, word):flag = -1for i in range(len(lst)):if lst[i] == word:flag = ibreakreturn flag
上面這段簡單代碼是求變量 word 在列表 lst 中出現(xiàn)的位置,我用這段來解釋“數(shù)據的具體情況”是什么意思。
變量 word 可能出現(xiàn)在列表 lst 的任意位置,假設 a = ['a', 'b', 'c', 'd']:
當 word = 'a' 時,正好是列表 lst 的第 1 個,后面的不需要再遍歷,那么本情況下的時間復雜度是 O(1)。
當 word = 'd' 或者 word = 'e' 時,這兩種情況是整個列表全部遍歷完,那么這些情況下的時間復雜度是 O(n)。
這就是數(shù)據的具體情況不同,代碼的時間復雜度不同。
根據不同情況,我們有了最好情況時間復雜度、最壞情況時間復雜度和平均情況時間復雜度這 3 個概念。
最好情況時間復雜度
最好情況就是在最理想的情況下,代碼的時間復雜度。對應上例變量 word 正好是列表 lst 的第 1 個,這個時候對應的時間復雜度 O(1) 就是這段代碼的最好情況時間復雜度。
最壞情況時間復雜度
最壞情況就是在最差的情況下,代碼的時間復雜度。對應上例變量 word 正好是列表 lst 的最后一個,或者 word 不存在于列表 lst,這個時候對應的時間復雜度 O(n) 是這段代碼的最壞情況時間復雜度。
平均情況時間復雜度
大多數(shù)情況下,代碼的執(zhí)行情況都是介于最好情況和最壞情況之間,所以又出現(xiàn)了平均情況時間復雜度。
那怎么計算平均時間復雜度呢?這個說起來有點復雜,需要用到概率論的知識。
在這里我還是用上面的例子來講,因為只是簡單的科普一下,為了方便計算,我假設的會有點隨意:
從大的方面來看,查找變量 x 在列表 lst 中的位置有兩種情況:在或者不在。假設變量 x 在或者不在列表 lst 中的概率都為 1/2。
如果 x 在列表 lst 中,那么 x 有 n 種情況,它可能出現(xiàn)在 0 到 n-1 中任意位置,假設出現(xiàn)在每個位置的概率都相同,都為 1/n。
每個出現(xiàn)的概率(即權重)知道了,所以平均時間復雜度為:
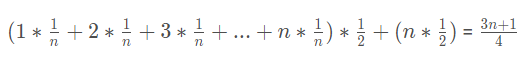
是不是看著有點眼熟,這就是我們都學過的加權平均值。
什么,沒學過?問題不大。加權平均值就是將各數(shù)值乘以相應的權數(shù),然后加總求和得到總體值,再除以總的單位數(shù)。
所以最終的平均時間復雜度就為:
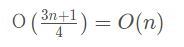
最好情況,反應最理想的情況,怎么可能天上天天掉餡餅,沒啥參考價值。
平均情況,這倒是能反映算法的全面情況,但是一般“全面”,就和什么都沒說一樣,也沒啥參考價值。
最壞情況,干啥事情都要考慮最壞的結果,因為最壞的結果提供了一種保障,觸底的保障,保障代碼的運行時間這個就是最差的,不會有比它還差的。
所以,不需要糾結各種情況,算時間復雜度就算最壞的那個時間復雜度即可。
空間復雜度
空間復雜度相較于時間復雜度來說,比較簡單,需要掌握的內容不多。
空間復雜度和時間復雜度一樣,反映的也是一種趨勢,只不過這種趨勢是代碼運行過程中臨時變量占用的內存空間。
代碼在計算機中的運行所占用的存儲空間吶,主要分為 3 部分:
代碼本身所占用的
輸入數(shù)據所占用的
臨時變量所占用的
前面兩個部分是本身就要占這些空間,與代碼的性能無關,所以我們在衡量代碼的空間復雜度的時候,只關心運行過程中臨時占用的內存空間。
空間復雜度記作 S(n),表示形式與時間復雜度一致。
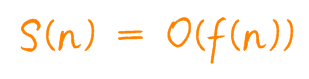
在這同樣 n 作為數(shù)據集大小,f(n) 指的是規(guī)模 n 所占存儲空間的函數(shù)。
空間復雜度分析
下面我們用一段簡單代碼來學習下如何分析空間復雜度。
def dogeggs_sum(lst):sum = 0for i in range(len(lst)):sum += lst[i]return sum
上述代碼是求列表 lst 的所有元素之和,根據之前說的,只計算臨時變量所占用的內存空間。
形參 lst 所占的空間不計,那么剩下的臨時變量只有 sum 和 i,sum 是存儲和,是常數(shù)階,i 是存儲元素位置,也是常數(shù)階,它倆所分配的空間和規(guī)模 n 都沒有關系,所以整段代碼的空間復雜度 S(n) = O(1)。
常見空間復雜度
常見的空間復雜度有 O(1)、O(n)、O(n2),O(1) 在上節(jié)講了,還有就是像 O(logn) 這種也有,但是等閑不會碰到,在這里就不羅嗦了。
O(n)
def create_lst(n):lst = []for i in range(n):lst.append(i)return lst
上面這段傻傻的代碼有兩個臨時變量 lst 和 i。
其中 lst 是被創(chuàng)建的一個空列表,這個列表占用的內存隨著 for 循環(huán)的增加而增加,最大到 n,所以 lst 的空間復雜度為 O(n),i 是存儲元素位置的常數(shù)階,與規(guī)模 n 無關,所以這段代碼最終的空間復雜度為 O(n)。
O(n2)
def create_lst(n):lst1 = []for i in range(n):lst2 = []for j in range(n):lst2.append(j)lst1.append(lst2)return lst1
還是一樣的分析方式,很明顯上面這段傻二次方的代碼創(chuàng)建了一個二維數(shù)組 lst,一維 lst1 占用 n,二維 lst2 占用 n2,所以最終這段代碼的空間復雜度為 O(n2)。
到這里,復雜度分析就全部講完啦,只要臭寶們認真看完這篇文章,相信會對復雜度分析有個基本的認識。復雜度分析本身不難,只要多加練習,平時寫代碼的時候有意識的多想估算一下自己的代碼,感覺就會慢慢來啦。
這是公眾號的第一篇,寫完真心不太容易,希望開了個好頭。碼字不易,臭寶們多多支持呀,點贊在看留言么么噠呀。
我是蛋蛋,我們下次見~

