何為時間復(fù)雜度與空間復(fù)雜度?
前言
所謂算法,其實就是我們用來操作數(shù)據(jù)、解決程序問題的一組方法。針對同一個問題,我們可以采用不同的算法,然后實現(xiàn)相同的結(jié)果。但是針對不同的算法,對于時間和資源的消耗卻有不同的差別。而為了分析不同算法的效率,我們常常從 時間 和 空間 兩個方面來對比,然后從中挑出最適合我們的解決方案。
本文主要從時間復(fù)雜度和空間復(fù)雜度的定義說起,然后介紹常見的時間復(fù)雜度和空間復(fù)雜度,最后則是對常見排序算法進行了總結(jié)。
時間復(fù)雜度
定義
若存在函數(shù) ,使得當 趨向無窮大時, 的極限值為不等于 0 的常數(shù),則稱 是 的同數(shù)量級函數(shù),記作 ,稱 為算法的 漸進時間復(fù)雜度,簡稱 時間復(fù)雜度,用大 O 來表示,稱為 大 O 表示法;
推導(dǎo)時間復(fù)雜度的原則
若運行時間是常數(shù)量級,則用常數(shù) 1 表示; 只保留時間函數(shù)中最高階項,如 ,保留最高階項后,成為 ; 若最高階項存在,則省去最高階項前的系數(shù),如 ,省去最高階項的系數(shù)后,成為 ;
分析時間復(fù)雜度的方法
總結(jié)起來,對于如何分析一段代碼的時間復(fù)雜度,主要有如下 3 個實用方法:
只關(guān)注循環(huán)執(zhí)行次數(shù)最多的一行代碼; 加法原則:總復(fù)雜度等于量度最大的那段代碼的復(fù)雜度; 乘法原則:嵌套代碼的復(fù)雜度等于嵌套內(nèi)外代碼復(fù)雜度的乘積;
常見的時間復(fù)雜度曲線
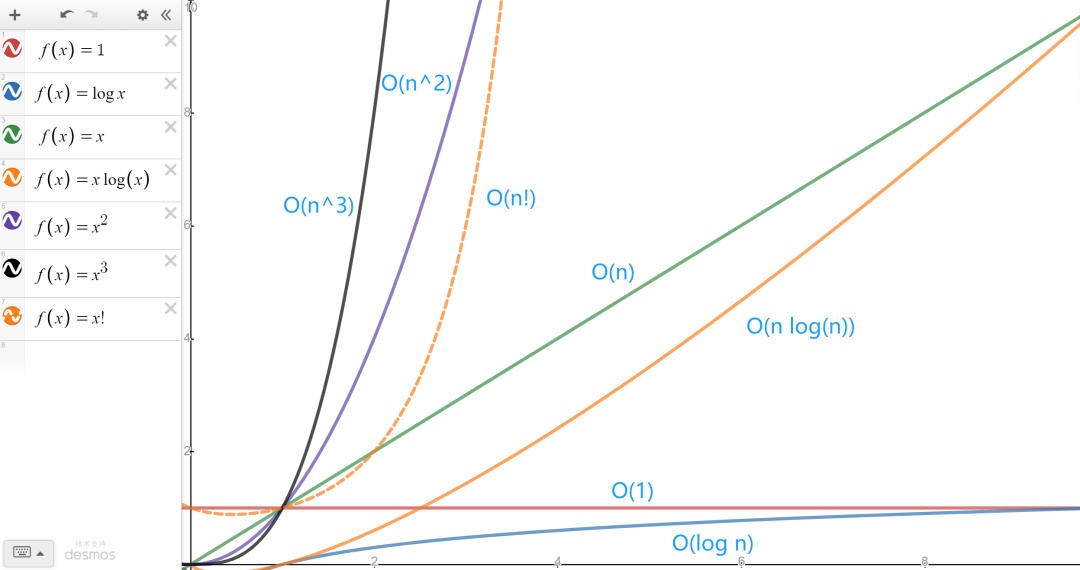
常見時間復(fù)雜度
即無論執(zhí)行多少行,都不會影響到其他區(qū)域,此時代碼的復(fù)雜度就是 ,如下面的代碼中,假設(shè)執(zhí)行每行代碼時間都相同切為 ,則 2,3 行各需 1 個執(zhí)行時間,即為 $t + t = 2t。此時執(zhí)行時間復(fù)雜度為常數(shù)。
void sayHello(String name){
System.out.prinln("Hello, " + String);
System.out.prinln("歡迎關(guān)注我的公眾號:【村雨遙】");
}
如下列二分查找代碼中,通過 while 循環(huán),能夠成倍的縮減搜索范圍,假設(shè)需要 x 次才能跳出循環(huán),則有 num * 2 * 2 * ... = n ,其中 num 是常數(shù),有 n 個 2 相乘,則有 ,從而推出 ,因此時間復(fù)雜度用大 O 表示法表示為
int binarySearch(int[] arr, int target){
int left = 0;
int right = arr.length - 1;
while(left <= right){
int middle = left + (left - right) / 2;
if(arr[middle] == target){
return middle;
}else if(arr[middle] > target){
right = middle - 1;
}else {
left = middle + 1;
}
}
return -1;
}
如下面這段代碼中,for 循環(huán)中的代碼被執(zhí)行了 arr.length 次,因此所需要的時間和數(shù)組長度成正比的,因此可以用 來表示它的時間復(fù)雜度。利用上述推到原則和分析的方法,可以知道下面代碼中循環(huán)次數(shù)最多的是 4,5 行,總的執(zhí)行時間是 ,拋去系數(shù)后,得到最終時間復(fù)雜度 .
int sum(int[] arr){
int total = 0;
for(int i = 0; i < arr.length; i++){
total += arr[i];
}
return total;
}
如果我們將一個復(fù)雜度為 的代碼重復(fù)執(zhí)行 次,那么此時代碼的復(fù)雜度不就變成 了嗎。
void hello (int n){
for( int i = 1 ; i < n ; i++){
int m = 1;
while( m < n ){
m *= 2;
}
}
}
假設(shè)我們將時間復(fù)雜度為 的代碼重復(fù)執(zhí)行 次,那么此時的時間復(fù)雜度就是 ,即可表示為 ,表現(xiàn)出來就是雙重循環(huán)的形式。
void selectionSort(int[] arr, int n){
for(int i = 0; i < n; i++){
int min = i;
for(int j = i + 1; j < n; j++){
if(arr[j] < arr[min]){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}
}
}
和 ,類似,將時間復(fù)雜度為 的代碼嵌套循環(huán)一次,此時復(fù)雜度就變成了 ,表現(xiàn)出來就是三重循環(huán)嵌套的形式。
void demo(int n){
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
for(int k = 0; k < n; k++){
System.out.print("Hello, World");
}
System.out.print("------");
}
System.out.print("******");
}
}
雖然理論上存在時間復(fù)雜度為 的算法,但實踐中基本遇不到,所以這里就不展開了。
空間復(fù)雜度
定義
空間復(fù)雜度是對一個算法在運行過程中臨時占用存儲空間大小的一個量度(即除開原始序列大小的內(nèi)存,在算法過程中用到的額外的存儲空間),反映的對內(nèi)存占用的趨勢,而不是具體內(nèi)存,也叫作 漸進空間復(fù)雜度 ,表示算法的存儲空間與數(shù)據(jù)規(guī)模間的增長關(guān)系,用 來代替;
常用空間復(fù)雜度
算法執(zhí)行所需臨時空間不隨某一變量 n 的大小而變化,則該算法空間復(fù)雜度為一個常量,表示為 ;
int num1 = 1;
int num2 = 2;
int total = num1 + num2;
數(shù)組占用內(nèi)存大小為 n,而且后續(xù)未分配新的空間,因此該算法空間復(fù)雜度為 ;
int[] arr = new int[n];
二維數(shù)組的情況;
int[][] arr = new int[n][n];
常見排序算法的時間復(fù)雜度和空間復(fù)雜度
對于面試中常見的的排序算法,以下總結(jié)給出了其時間復(fù)雜度以及空間復(fù)雜度,以及算法穩(wěn)定性。
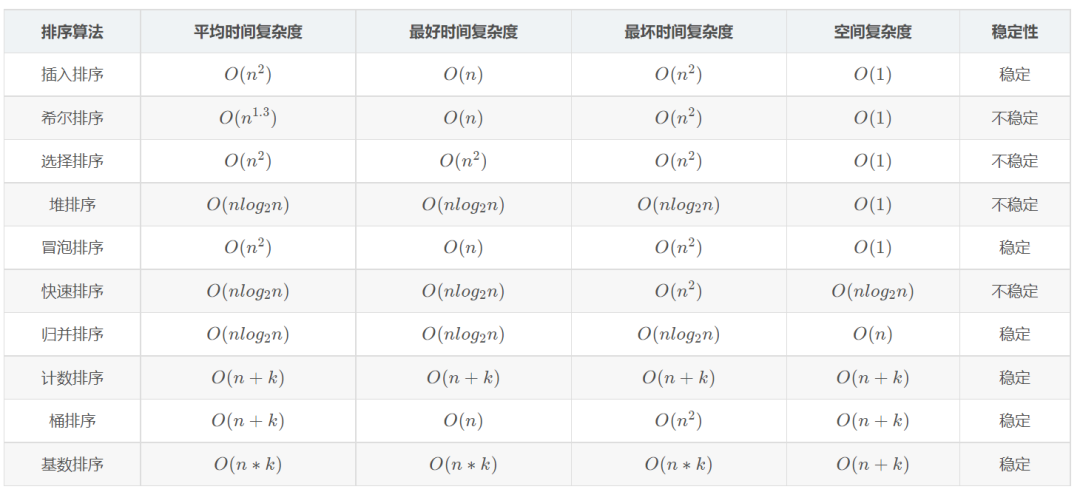
總結(jié)
好了,以上就是今天文章的內(nèi)容了。主要介紹了時間復(fù)雜度的定義、推導(dǎo)原則以及常見時間復(fù)雜度,還對空間復(fù)雜度定義以及常見空間復(fù)雜度進行了介紹,最后則是總結(jié)了常見排序算法的時間復(fù)雜度和空間復(fù)雜度。如果覺得文章對你有所幫助,那就點個贊再走吧!