圖像特征點、投影變換與圖像拼接

點擊上方“小白學(xué)視覺”，選擇加"星標"或“置頂”

重磅干貨，第一時間送達

一、全景拍照中的投影變換

在32. 鏡頭、曝光，以及對焦（下）中，我給你介紹了各種各樣的相機鏡頭，也介紹了視場角（FOV）這個概念。現(xiàn)在咱們手機上的主攝像頭一般FOV是七、八十度左右，有的更小一些。但人類的視覺系統(tǒng)FOV可以達到??。

廣角鏡頭、魚眼鏡頭能夠讓你拍攝出非常大FOV的圖像。但它們非常昂貴，而且具有強烈的畸變。

全景拼接這個功能也能夠讓你拍攝出很大FOV的圖像，你很可能已經(jīng)使用過這個功能了，它甚至可以拍攝出水平FOV達到360o的圖像。我們可以比較下。這樣拍攝出來的圖像比起魚眼鏡頭的畸變小很多。

全景拼接是通過先拍攝不同視角的多張圖像，然后將它們拼接而成的：

那么，像下面這樣幾個視角拍攝的圖像，我們是不是直接拼接平移這些圖像然后拼接就可以了呢？

很顯然，不管我們是把左邊的圖像擺在上面，還是把右邊的圖像擺在上面，都會觀察到“對不齊”的現(xiàn)象（看看中間欄桿的斷裂縫）：

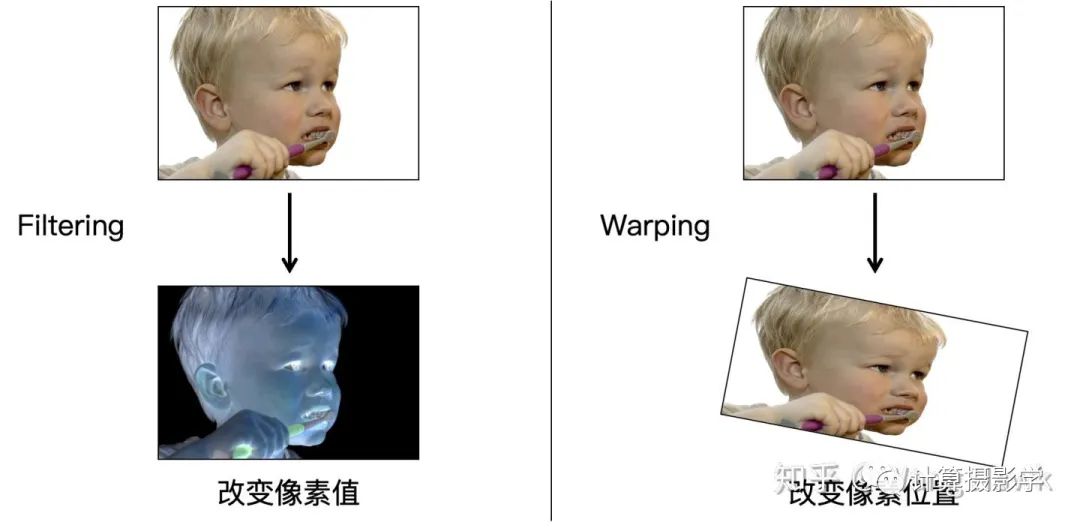
那應(yīng)該怎么辦呢？這時候就要用到我在28. 圖像扭曲中介紹的圖像的Warping技術(shù)。適當?shù)腤arp圖像然后再做拼接，能夠使得我們得到完美的全景圖像：

Warping是一種改變圖像像素位置的技術(shù)

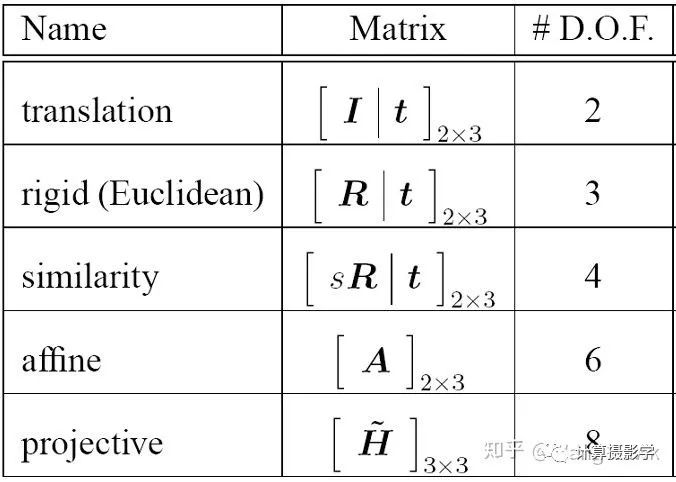
各種類型的2D圖像變換都可以用變換矩陣來表示，如下圖所示，其中包括平移變換(Translation)、剛體變換(Rigid)、相似變換(Similarity)、仿射變換(Affine)、投影變換(Projective)。

它們具有不同的內(nèi)核和自由度：

那么，在全景拼接中我們用什么樣的變換矩陣呢？事實上，此時我們通常采用的是投影變換，因為它的能力比起上面其他的變換形式都更強。下面是同樣兩張圖像，三種不同變換形式的拼接結(jié)果，可以看到投影變換的結(jié)果是最自然正確的：

投影變換不僅僅用于全景拼接，我們還可以使用它來做視角變換，比如把正視圖變換為俯視圖或側(cè)視圖：

還可以用來模擬旋轉(zhuǎn)視角：

校正多幅圖像：

事實上，不僅僅是在數(shù)字圖像處理時代人們使用投影變換，在平常的生活中人們早就在利用投影變換了。比如，你很可能了解甚至親眼見過3D繪畫，藝術(shù)家利用透視原理在地上作畫，從而在某一個視角觀看時可以有非常逼真的3D效果。這事實上是一種將2D圖像反向變換為3D圖像的過程。

藝術(shù)家也早就將投影變換應(yīng)用到了畫作中，例如下面這幅圖左上角的人物腳下踩著的地面，就遵循投影變換中近大遠小的規(guī)律。

而我們甚至可以反向利用投影變換，來看看他們腳下的圖案的實際樣子。可以想到畫作作者傾注了多少心血在細節(jié)上：

文藝復(fù)興時代投影變換剛剛被發(fā)現(xiàn)，所以類似上面的這種表現(xiàn)形式在那時候的畫作中經(jīng)常出現(xiàn)：

有一幅著名的油畫叫做“大使們”，是畫家小漢斯·霍爾拜因的作品。這幅畫有非常多的解讀，尤其是在畫作前景有一個奇怪的、扭曲的物體：

可以利用反向投影變換將這個局部圖像校正到正常的視角，原來是一個可怕的頭骨：

事實上，還可以利用一些生活中常見的物體，例如一個勺子，來實現(xiàn)圖像扭曲，從而理解畫作中的物體。（將勺子靠近畫作，勺子表面的曲面反射光線，從而可以讓你看清畫里面的物體）

二、什么時候可以使用投影變換

好了，你已經(jīng)看到在繪畫和全景拼接時，我們通常可以采用投影變換（又稱為單應(yīng)變換）來Warp圖像，從而得到預(yù)期的結(jié)果。那么問題來了？投影變換在什么場景下適用，什么情況下不適用呢？

還是讓我們看看29. 小孔相機的模型：

可以看到小孔成像時，物體方向的光線總是會通過共同的相機中心。這意味著拍照時，我們只是在用圖像平面來選擇部分光線。

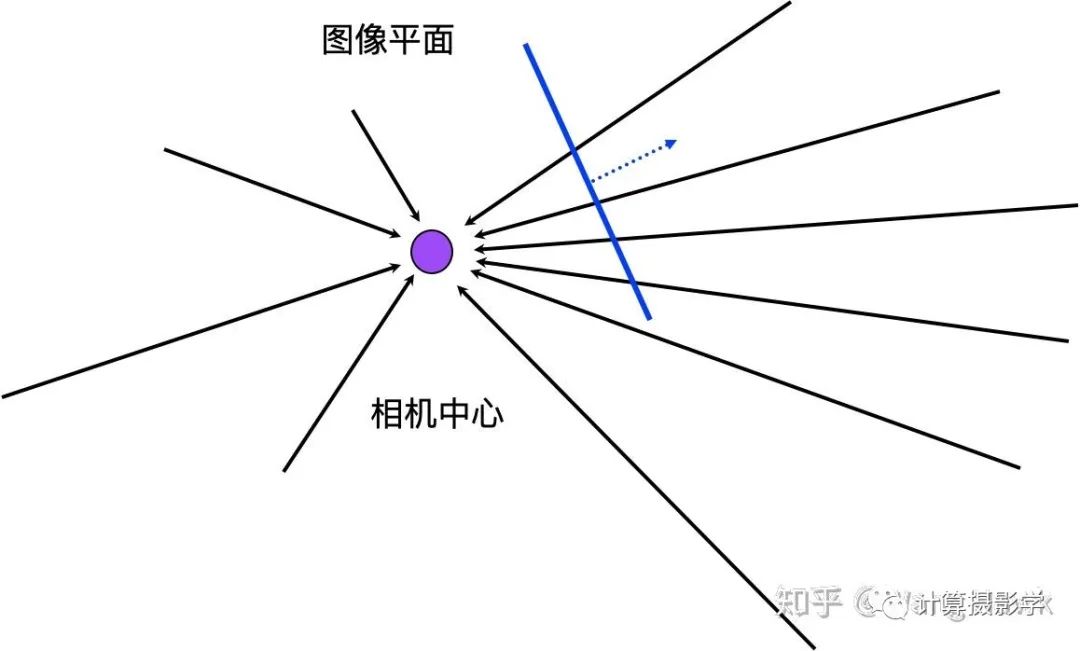
當我們用2D投影變換來講圖像變換到新的視角時，情況如下：

這里你可以看到，只要新的視角和原始視角有共同的光學(xué)中心，并且和原視角有共同的視線范圍，就可以將原始視覺的圖像利用投影變換變換到新的視角下。

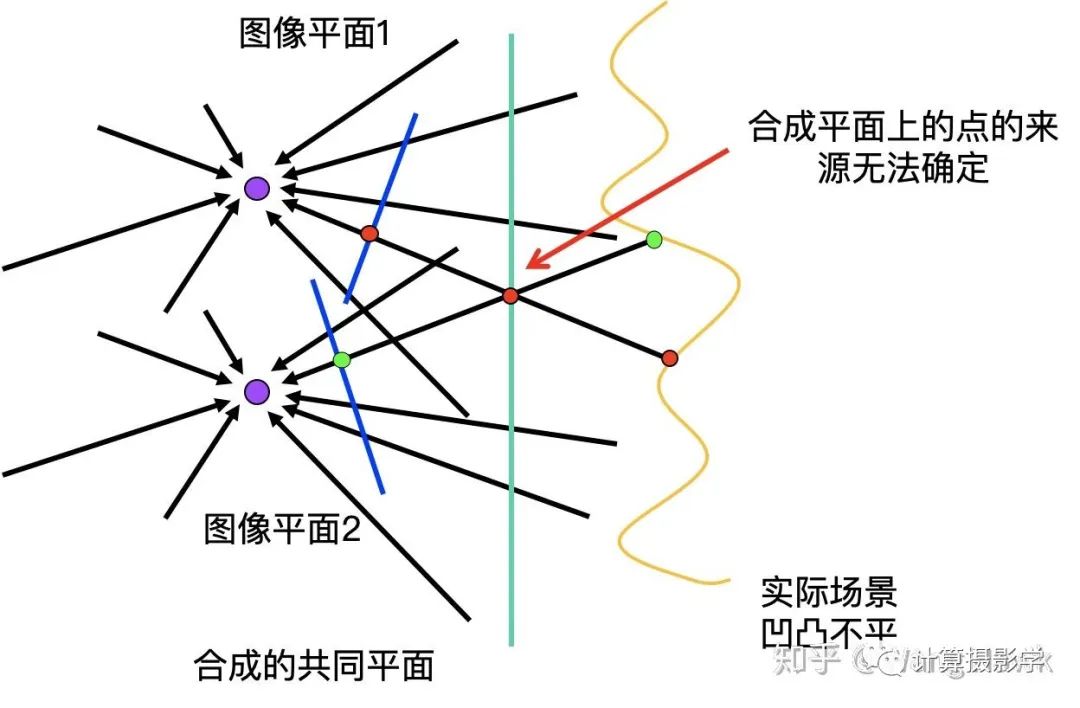
而在全景拼接中，假如我們要把在不同相機中心位置拍攝的圖像通過投影變換拼接到一起時，會怎么樣呢？比如下圖，我們要將圖像平面1和2通過投影變換到綠色線表示的共同平面上去，從而實現(xiàn)拼接，此時會怎樣呢？

這個時候，你會發(fā)現(xiàn)合成平面上的點很可能會出現(xiàn)無法確定來源的情況，這實際上就是由于“視差”導(dǎo)致的。也就是說，在圖像拼接時，2D投影變換（也稱為單應(yīng)變換）無法應(yīng)對相機中心平移導(dǎo)致的視差現(xiàn)象。

但在少量的情況下，即便相機中心平移，也可以采用投影變換，如果：

如果你使用過微軟的Onenote，或者“名片全能王”、“掃描全能王”這樣的軟件，你可以看到它們能比較好的將名片，或是照片等轉(zhuǎn)換為正視圖。其中也就利用了對平面物體采用投影變換的原理——特別要注意的是，采用這種方式，不需要知道實際相機的物理參數(shù)，純粹采用2D圖像變換即可做到。

三、投影變換矩陣的計算

投影變換矩陣，正如上面所講，是一個3X3的矩陣，其中一共有8個自由度。一個圖像上的點P變換到另外一個圖像上的點P'的過程用下式來描述，其中H是2D投影變換矩陣，也稱為單應(yīng)矩陣。

將矩陣乘法展開可得：

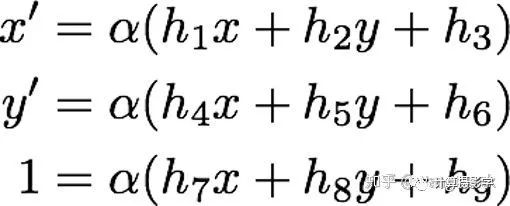
拋棄尺度量后有：

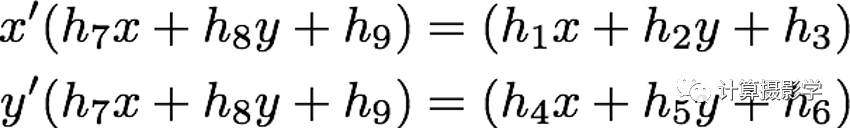
再稍加整理有：

所以如果知道原始圖像和變換后的圖像的一對對應(yīng)點的坐標，可以構(gòu)成兩個線性方程。因此，如果要確定變換矩陣中的8個未知量，一共需要4對對應(yīng)點，8個線性方程：

我們將上式寫作矩陣和向量的乘法有：

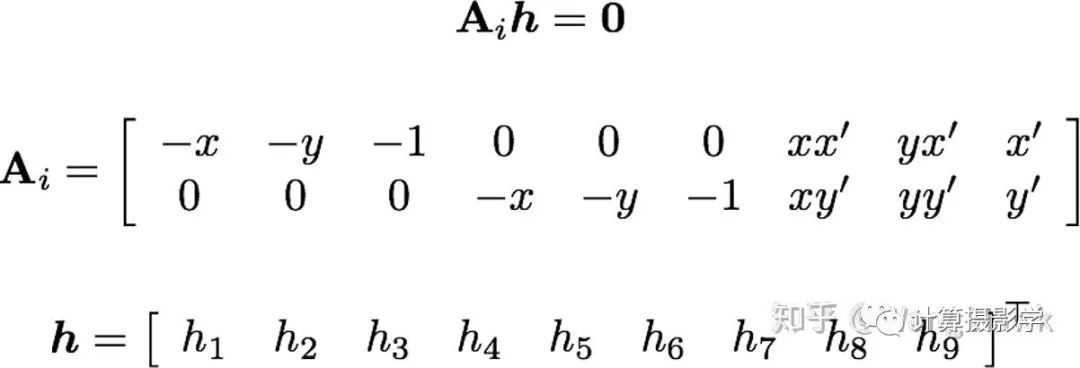
這樣又多個對應(yīng)點時，就成了：

這里的A可以是正定的（未知數(shù)==方程個數(shù)），也可以是超定的（未知數(shù)<方程個數(shù))。可以簡單的利用SVD分解來求解上述方程得到H，從而進行圖像的變換。

在上面的過程中，我們忽略了獲取不同圖像視角對應(yīng)點坐標的過程，事實上可以手動指定圖像的對應(yīng)坐標點來計算出單應(yīng)矩陣。比如在“名片全能王”這樣的應(yīng)用中，就是通過檢測到名片的四個角位置，然后指定屏幕上的名片框的四個角的位置，從而計算出單應(yīng)矩陣并進行名片圖像的變換的。

但是實際我們要做圖像拼接的場景通常比名片更加復(fù)雜，沒有可以輕易指定的邊框角，有沒有更智能的方法來獲取圖像間的對應(yīng)點呢？這就是下一節(jié)所要講的。

四、圖像對齊時的特征點獲取

正如上面所講，要計算圖像視角間的變換矩陣，需要確定圖像的對應(yīng)點的位置。那么什么樣的點適合這個用途呢？我上面講過名片全能王這樣的應(yīng)用采用的是名片的四角點，那么對于其他自然場景呢？

比如說上圖，其中我們選擇的點要求：

• 在兩個視角中都很顯著

• 在兩個視角中都容易檢測

• 不會和其他的點混淆

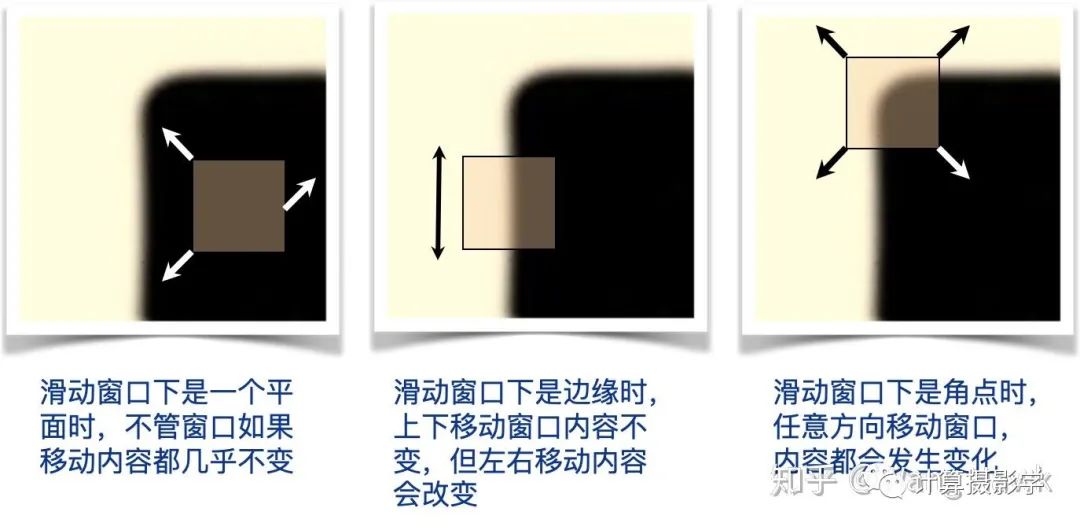
我們稱這種點為”特征點“。有一種基礎(chǔ)的，容易理解的特征點為”角點“，通過下圖很容易可以理解：

有一種著名的角點檢測算法是"Harris Corner”檢測算法，其過程也非常容易理解：

稍稍解釋下期中的關(guān)鍵步驟：

我已經(jīng)在3. 數(shù)碼相機內(nèi)的圖像處理-基本圖像濾波中介紹過圖像的梯度計算方法，而這里我們要求在一個很小的局部窗口內(nèi)計算每個像素點的梯度值：

將梯度減去平均值，則是為了做一定程度的歸一化. 利用這個歸一化的梯度值，我們可以計算協(xié)方差矩陣，從而擬合一個拋物面（注意下圖的P，代表梯度計算的局部圖像塊）

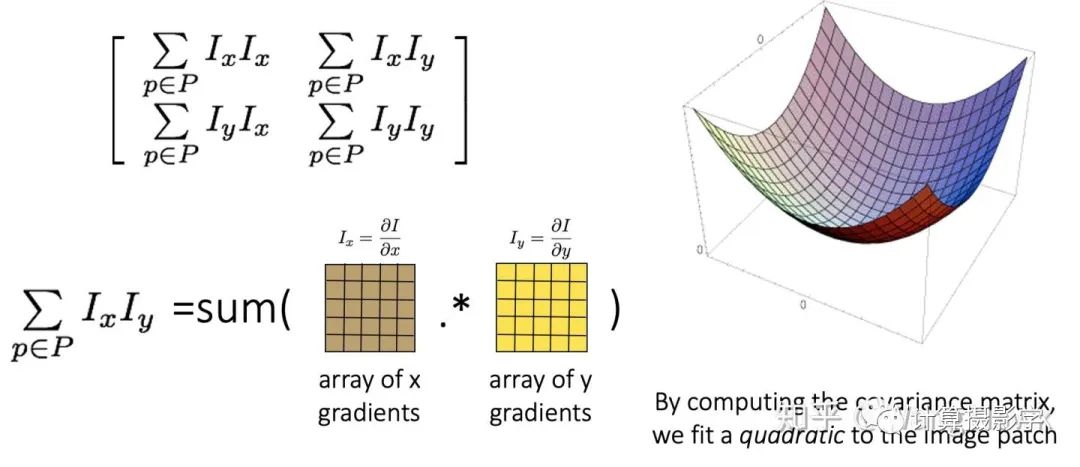
這個協(xié)方差矩陣的特征向量有著特殊的意義，它可以寫作下式，從而反應(yīng)出圖像局部點的特點：

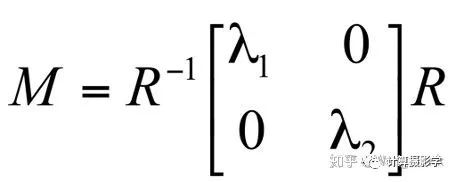
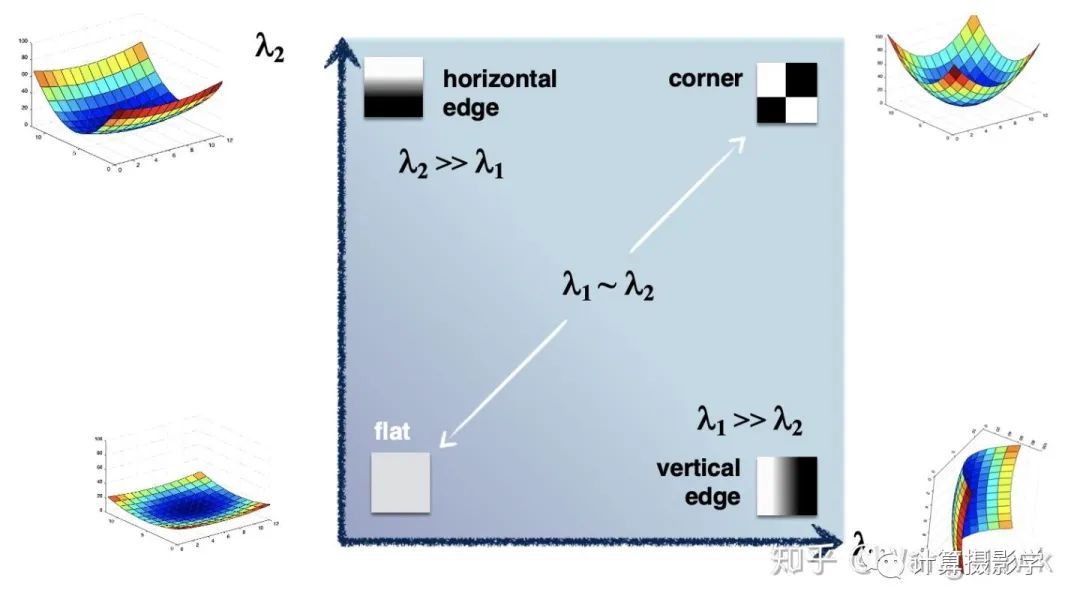
可以看到，只有兩個特征值都比較大且沒有明顯的差距時，才是角點。因此可以通過??來確定是否是角點。更流行的方法則是通過下面的Harris角點檢測算子來確定是否是角點，相比使用??這個算子計算量更小。

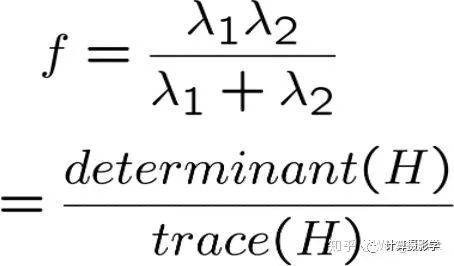
當然兩者其實都很相似：

在實際使用時，會發(fā)現(xiàn)局部區(qū)域有大量點都滿足算子>threshold的條件，因此還需要采用“非極大值抑制”的方法，選擇局部區(qū)域算子最大的點作為最終的特征點。我們來實際看看在圖像中尋找角點的過程：

五、總結(jié)

今天這篇文章從全景拼接開始，講到了拼接中采用的2D圖像變換主要是單應(yīng)變換（投影變換），然后再講了單應(yīng)變換矩陣的直接計算方法。我們看到只需要知道至少4個非共線的點對就可以確定單應(yīng)變換矩陣。最后講了一種非常簡單直觀的獲取圖像特征點的方式——Harris Corner檢測法。

事實上，圖像的特征點檢測還有很多高級的方法，你一定聽說過像SIFT/SURF/ORB等方式，事實上從2003年SIFT的作者D.G.Lowe就另外一名大牛M. Brown合寫了文章Recognising Panoramas，其中就用SIFT特征點來作為圖像變換關(guān)系的計算基礎(chǔ)。

由于篇幅原因，本文不再對此做展開，將來有機會時再深入探討全景拼接中的高級方法。

六、參考資料

今天的主要參考資料為：

• CMU 2017 Fall Computational Photography Course 15-463, Lecture 19

• M. Brown and D. Lowe，Recognising Panoramas， 2003