三種集成學習算法原理及核心公式推導
導讀
本文主要介紹3種集成學習算法的原理及重要公式推導部分,包括隨機森林(Random Forest)、自適應(yīng)提升(AdaBoost)、梯度提升(Gradient Boosting)。僅對重點理論和公式推導環(huán)節(jié)做以簡要介紹。
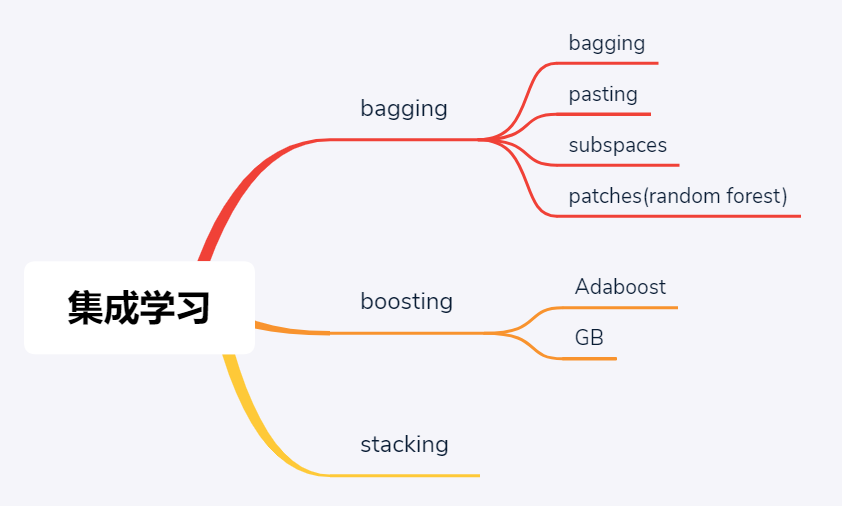
集成學習3大流派
在經(jīng)典機器學習場景下,當單個學習模型性能不足以有效滿足算法精度時,人們開始向集成學習模型發(fā)力——其思想和出發(fā)點很直觀,就是三個臭皮匠賽過諸葛亮。進一步地,根據(jù)這三個臭皮匠在致力于賽過諸葛亮期間的協(xié)作模式不同,集成學習又細分為bagging和boosting兩大學派,其中前者是并行模式,意味著三個臭皮匠各搞各的然后將最后結(jié)果進行融合以期帶來提升,這里bagging是一個合成詞匯,本意為booststrap aggregating;后者是串行模型,先讓一個臭皮匠去探探底,根據(jù)反饋結(jié)果再派第二個、第三個,頗有些車輪戰(zhàn)的味道。進一步的,車輪戰(zhàn)還可以根據(jù)具體戰(zhàn)術(shù)落腳點的不同,而分為Adaboost和GB,其中AdaBoost算法中各個臭皮匠的迭代重點在于不斷彌補自己的過失/錯誤的地方,而GB算法中各個臭皮匠的迭代重點在于不斷彌補自己與諸葛亮/理想型的差距,或者說殘差。
當然,除了bagging和boosting兩大流派之外,其實集成學習還有第三大流派——stacking,從其名字可以看出端倪是有些堆棧的意味,其實質(zhì)就是將前一輪學習之后的輸出/標簽組織變換后作為下一輪學習的輸入/特征,然后再次訓練。其實就是深度學習那一套……
隨機森林是典型的bagging流派集成學習算法,個人非常喜歡這個算法的名字:森林二字可以窺探出這個算法是源于決策樹,當以多棵樹作為弱學習器,那么組成的集成學習算法自然叫做森林最合適;而隨機二字則形象的體現(xiàn)其在構(gòu)建每棵決策樹時,實際上是采取了隨機采樣的方式來確保各弱學習器結(jié)果的多樣性。至于為什么要保證多樣性,稍后的公式推導可以說明這一點。
這里,既然說隨機森林是bagging流派的典型代表,那么言外之意就是還存在其他bagging算法,實際也正是如此。廣義來講,bagging流派集成學習算法可分為4類,主要差別主要源于采樣方式的不同:
僅對樣本維度(體現(xiàn)為行采樣)進行采樣,且采樣是有放回的,意味著每個弱學習器的K個采樣樣本中可能存在重復(fù)的樣本,此時對應(yīng)bagging算法,這里bagging=bootstrap aggregating。發(fā)現(xiàn),這個具體算法的名字與bagging流派的名字重合,這并不意外,因為這是bagging中一種經(jīng)典的采樣方式,因而以其作為流派的名字。當然,bagging既是一種算法也是流派名,那就要看是狹義還是廣義的bagging來加以區(qū)分了
僅對樣本維度采樣,但采樣是無放回的,意味著對于每個弱學習器的K個采樣樣本是完全不同的,由于相當于是每執(zhí)行一次采樣,則該樣本就被舍棄掉(pass),所以此時算法叫做pasting
前兩者的隨機性均來源于樣本維度的隨機采樣,也就是行方向上,那么對于列方向上進行隨機采樣是否也可以呢?比如說每個弱學習器都選用所有的樣本參與訓練,但各學習器選取參與訓練的特征是不一致的,訓練出的算法自然也是具有隨機性的,可以滿足集成的要求。此時,對應(yīng)算法叫做subspaces,中文譯作子空間,具體說是特征維度的子空間,名字還是比較傳神的
發(fā)現(xiàn),既有樣本維度的隨機,也有特征維度的隨機,那么自然想到有沒有兼顧二者的隨機呢,也就是說每個弱學習器既執(zhí)行行采樣、也有列采樣,得到的弱學習器其算法隨機性應(yīng)該更強。當然,這種算法被稱作是patches,比如前文已經(jīng)提到的隨機森林就屬于這種。實際上,隨機森林才是最為廣泛使用的bagging流派集成學習算法
發(fā)散一下,其實bagging算法無非就是區(qū)分到底是行采樣、列采樣還是行列采樣,那為什么會出來4種呢?原來是行采樣在采樣執(zhí)行過程中又細分了是否有放回。那既然行采樣可以區(qū)分是否有放回,列采樣是否也可區(qū)分一下衍生出兩種具體算法呢?實際上是不可以的,因為特征的有放回意味著特征重復(fù),在機器學習訓練過程中重復(fù)的特征或者說復(fù)制特征參與訓練不能帶來學習效果的改變;但樣本的重復(fù)或者說復(fù)制則能帶來學習效果的差異,因為這直接帶來算法訓練樣本的類別平衡性,自然影響訓練結(jié)果。
bagging算法原理非常簡單易懂,算法出發(fā)點也非常樸素,其中涉及到的公式推導也不多,主要需要理解以下三個要點:
有放回采樣中,預(yù)計有36.8%的樣本不會被用于訓練,也就意味著這些樣本可以天然的作為測試集用于評估集成學習模型效果。36.8%是如何而來呢?設(shè)樣本數(shù)量為N,則對任意樣本而言在1次采樣中不被抽中的概率為 1 - 1/N,在N次采樣中均未被抽中的概率則為
bagging流派的各種算法中,一直在強調(diào)每個弱學習器訓練效果之間的隨機性,或者說差異性,那么為什么要保證這種差異性呢?直觀來看,把集成學習比作是一次考試,A同學在參考了周邊的BCD3名同學答案的基礎(chǔ)上做判斷,如果BCD3人的答案都是一樣的,正確的都正確,錯誤的都錯誤,那么A同學的在綜合3人答案之后絲毫不會對最終結(jié)果帶來任何提升,仍然是BCD三人的正確率。而只有當3人擅長的考點不一樣得出的答案也不盡相同時,A綜合之后才可能帶來提升。具體到其中一道題,用數(shù)學語言描述就是:設(shè)BCD三人答對的概率分別為Pb、Pc、Pd,如果三人答案的正確與否是獨立事件,那么A本著少數(shù)服從多數(shù)的原則,得到正確答案的概率為PbPc(1-Pd) +?(1-Pb)PcPd + Pb(1-Pc)Pd + PbPcPd;反之,如果三人答案的正確與否是相關(guān)聯(lián)的事件,即同時正確或錯誤,那么A的最終正確率其實是不變的。所以,bagging流派要求集成學習各弱學習器之間要求算法盡可能是隨機的,同時也有準確率的最低要求,即不能低于50%,否則會對集成效果帶來負作用
bagging流派將帶來算法的低方差,但不會降低偏差。衡量機器學習模型效果時,往往需要考慮偏差和方差兩方面因素,偏差意味著模型訓練效果距離理想目標還有很大差距,常常效果很差;方差意味著模型訓練效果時好時壞,雖然有時候效果很好,但不夠穩(wěn)定,二者的形象描述示意如下圖所示。那么,當我們說bagging集成學習相較于單個弱學習器效果有所提升,具體是指哪方面有所提升呢,換言之是降低了偏差還是方差呢?答案是偏差不變,方差降低。這可以由以下兩個公式意會的表達:
當然,以上兩個公式也僅可意會的表達集成學習效果的提升,而不能具體刻畫。實際中的bagging算法當然是會帶來偏差的降低,只是統(tǒng)計意義下的均值與弱學習器效果相當,具體如何降低偏差那就需要具體問題具體調(diào)參了!
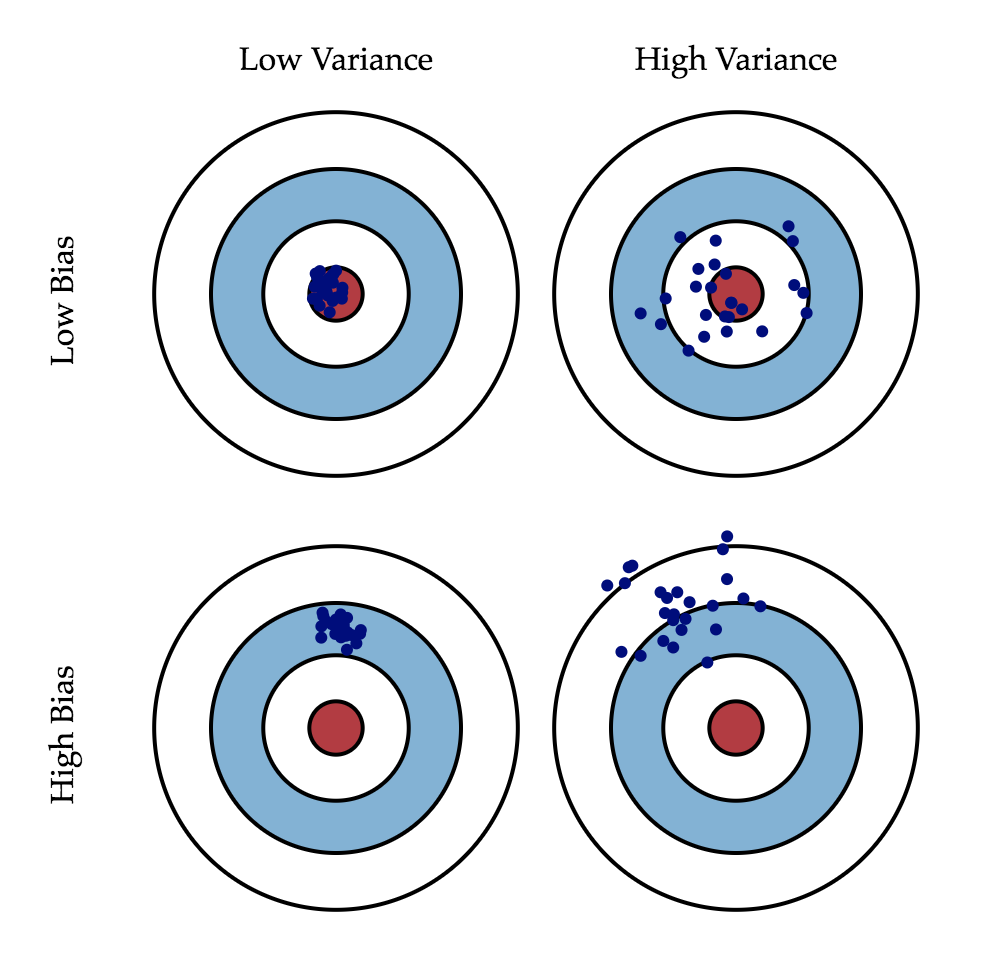
理解機器學習方差和偏差
圖片源于《Understanding the Bias-Variance Tradeoff 2012》一文
原文鏈接:http://scott.fortmann-roe.com/docs/BiasVariance.html
此外,bagging流派由于是并行訓練多個模型,而后綜合各個弱學習器的效果進行綜合決策,那么綜合決策的方式其實也是一個值得探討的問題。簡言之,就是hard voting和soft voting兩種方式,以二分類問題為例,前者是直接統(tǒng)計所有弱學習器的結(jié)果,然后取其中結(jié)果最多的那一類作為最終結(jié)果;而后者則不是直接統(tǒng)計結(jié)果,而是統(tǒng)計各弱學習器的分類概率,并分別計算所有弱學習器中兩類的概率之和,以概率之和較大者作為最終結(jié)果。具體不再贅述。
與bagging流派集成學習思想不同,boosting流派側(cè)重于后人站在前人的肩膀上看問題,Adaboost和GB概莫能外。當然,雖然理論上最后一個弱學習器在綜合了所有前人的經(jīng)驗基礎(chǔ)上可能會具有最好的性能,但Adaboost也不是簡單的以最后的弱學習器結(jié)果為準,而是仍然加權(quán)考慮所有弱學習器的結(jié)果。
前文提到,Adaboost算法在吸取前一個弱學習器訓練效果的基礎(chǔ)上,重點關(guān)注錯誤的樣本從而針對性的執(zhí)行后續(xù)訓練過程,具體說就是加大前一輪訓練錯的樣本權(quán)重。
以二分類為例,Adaboost算法核心算法原理(公式推導):
損失函數(shù):指數(shù)函數(shù),當訓練結(jié)果與真實標簽一致時(乘積為正)損失較小,不一致時(乘積為負)損失較大
m輪訓練后的集成學習模型:前m個弱學習器的加權(quán)求和
m輪訓練后的模型損失
其中em表示第m輪弱學習器的模型訓練錯誤率,根據(jù)錯誤樣本的權(quán)重之和與總樣本的權(quán)重之和比值得出。當然在樣本權(quán)重和進行歸一化的基礎(chǔ)上,分母為1。
然后分析每輪訓練弱學習器時的樣本權(quán)重迭代方式。再看損失函數(shù),每個樣本的損失可看做是兩部分的乘積形式,其中前一部分與第m輪訓練的弱學習器Gm(X)無關(guān),而后一輪與其直接相關(guān),因而可將前一部分看做是樣本加權(quán)系數(shù)——這也正是不斷調(diào)整每一輪訓練模型的樣本權(quán)重的根源所在。記第m輪訓練弱學習器的第i個樣本的權(quán)重系數(shù)為:
則可進一步發(fā)現(xiàn)權(quán)重的更新策略為:
也就是說,下一輪的樣本權(quán)重由前一輪樣本權(quán)重和前一輪的弱學習器訓練結(jié)果有關(guān),進一步地,當前一輪訓練結(jié)果與真實標簽一致時樣本權(quán)重前的系數(shù)為小于1的值,體現(xiàn)為樣本權(quán)重降低;否則權(quán)重增大。當然,在每輪更新后還需對樣本權(quán)重加和進行歸一化處理。
與Adaboost算法類似,GB(梯度提升)集成學習算法也是基于多個弱學習器的訓練效果的加權(quán)進行最終判決,且每輪訓練也基于前一輪訓練效果進行針對性的更新迭代。但與Adaboost聚焦于前一輪訓練錯誤的樣本機制不同,GB聚焦于前一輪訓練后的殘差,相當于是通過集成學習來了個算法接力,以使得最終學習效果不斷逼近真實水平。
對比fm(X)的梯度和其迭代公式,可知第m輪訓練的弱學習器實際上即為擬合當前殘差的弱學習器,這也正是GB的核心思想。實際上,GB也被稱作是函數(shù)空間的梯度下降法。
這是GB集成學習算法的出發(fā)點,也是理解不斷擬合殘差的核心。后續(xù)相關(guān)公式推導不再給出。
相關(guān)閱讀:
