二分查找算法（下）：通過 LeetCode 周賽學(xué)習(xí)二分查找算法

重磅干貨，第一時間送達(dá)

一個二分查找算法和貪心算法結(jié)合的場景

之所以寫這個，是因為我前兩周在參加 LeetCode 周賽的時候，碰到了一個這樣題，點(diǎn)擊「閱讀原文」可以直達(dá)題目鏈接，題目具體如下：

1648. 銷售價值減少的顏色球

你有一些球的庫存 inventory ，里面包含著不同顏色的球。一個顧客想要 任意顏色 總數(shù)為 orders 的球。

這位顧客有一種特殊的方式衡量球的價值：每個球的價值是目前剩下的 同色球 的數(shù)目。比方說還剩下 6 個黃球，那么顧客買第一個黃球的時候該黃球的價值為 6 。這筆交易以后，只剩下 5 個黃球了，所以下一個黃球的價值為 5 （也就是球的價值隨著顧客購買同色球是遞減的）。

給你整數(shù)數(shù)組 inventory ，其中 inventory[i] 表示第 i 種顏色球一開始的數(shù)目。同時給你整數(shù) orders ，表示顧客總共想買的球數(shù)目。你可以按照 任意順序 賣球。

請你返回賣了 orders 個球以后 最大 總價值之和。由于答案可能會很大，請你返回答案對 10 ** 9 + 7 取余數(shù) 的結(jié)果。

示例 1：

輸入：inventory = [2,5], orders = 4

輸出：14

解釋：賣 1 個第一種顏色的球（價值為 2 )，賣 3 個第二種顏色的球（價值為 5 + 4 + 3）。

最大總和為 2 + 5 + 4 + 3 = 14 。

提示

• 1 <= inventory.length <= 10 ** 5

• 1 <= inventory[i] <= 10 ** 9

• 1 <= orders <= min(sum(inventory[i]), 10 ** 9)

分析

剛開始我完全沒有意識到有二分查找的思想，就是想著用一個優(yōu)先隊列，然后每次取出一個元素，加上當(dāng)前值，把當(dāng)前值減一，然后再把當(dāng)前值放入優(yōu)先隊列。

沒過幾分鐘，程序就寫完了，但是呢提交后顯示運(yùn)行超時了，我就想著去優(yōu)化程序。于是我又讀了下題，看看是不是我漏了啥重要條件，結(jié)果讀了幾遍發(fā)現(xiàn)這道題就是貪心的思想啊，不可能錯的呀，但是結(jié)果就是超時了。。。

于是周賽結(jié)束后我特意去查了下大神寫的代碼，真的是讓我驚呆了，是貪心的思想沒錯，但是是二分和貪心進(jìn)行結(jié)合。

這個題想法很簡單，設(shè)置一個 sum 變量，sum 每次加上數(shù)組中的最大值，然后將當(dāng)前值減去 1，直到此過程重復(fù) orders 步驟。

然后為啥用優(yōu)先隊列會超時呢？其實優(yōu)先隊列的底層就是堆，每次取出元素，加入元素都需要對堆進(jìn)行調(diào)整，調(diào)整的時間復(fù)雜度是 O(logn),其中 n 是優(yōu)先隊列的長度，然后需要進(jìn)行 orders 操作，所以總的時間復(fù)雜度就是 O(Nlogn), 其中 N 是 orders， n 是數(shù)組長度。

而這道題的話，orders 會取到 10 ** 9,所以自然而然就會超時了。

那么應(yīng)該如何解決呢？

解決思路

既然單獨(dú)使用優(yōu)先隊列解決不了問題，那我們就換個思路進(jìn)行思考。因為每次都要取數(shù)組中的最大值，然后減去 1, 所以最后呢數(shù)組中的元素肯定是小于等于某一個閾值的，這個我想你肯定是能夠理解的。

那這個閾值能不能求出來呢？如果能求出來的話，那問題是不是就容易解決了呢？你想啊，如果現(xiàn)在我們已經(jīng)求出了這個閾值，那么是不是就知道了數(shù)組中的每個元素被減了多少次，進(jìn)而累加求和不就得到結(jié)果了嘛。

好，現(xiàn)在問題已經(jīng)變成了如何求解閾值了，這個如何求解呢？我們假定閾值為 threshold,那么它滿足啥條件呢？

怎么理解呢？

就是說當(dāng)前值是 threshold時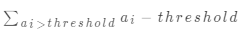， 就代表了所有的操作的次數(shù)，它應(yīng)該是小于等于 orders的，為啥呢？拿例 1 舉例，數(shù)組為 [2, 5], orders 為 4,相當(dāng)于要進(jìn)行四次操作。

1. 5 減 1,變?yōu)?4

2. 4 減 1,變?yōu)?3

3. 3 減 1,變?yōu)?2

4. 剩下兩個 2, 2 減 1,變?yōu)?1

此時所有數(shù)組中的元素都小于等于 2,所以這個例子中的 threshold就是 2。但是有可能出現(xiàn)小于 orders 的情況，比如文中的這個例子，這時候又需要當(dāng)前數(shù)組中的部分元素再減去 1,但是又不能所有元素都減去 1,如果那樣的話， threshold 就會改變了。

因為這個函數(shù)是一個單調(diào)遞減的函數(shù)，所以存在唯一的 threshold,滿足上述式子。所以問題就轉(zhuǎn)化為了在 0 和 10 ** 9 之間查找最小的 threshold,使得

看到了嗎？這個問題就轉(zhuǎn)化為了上篇文章中我們提到的二分算法的變體問題，沒理解的話，你品，你再品。

然后就表示了數(shù)組中元素還需要再減 1 的次數(shù)。

這個問題到這里就解決了，接下來看看代碼吧，這里面還有很多騷操作，保證出乎你的意外。

代碼實現(xiàn)

 1class?Solution:
 2????def?maxProfit(self,?inventory:?List[int],?orders:?int)?->?int:
 3????????max_num?=?10?**?9?+?7
 4????????res?=?0
 5????????low,?high?=?0,?10?**?9
 6????????threshold?=?None
 7????????while?low?<=?high:
 8????????????mid?=?low?+?((high?-?low)?>>?1)
 9????????????temp?=?0
10????????????for?i?in?range(len(inventory)):
11????????????????if?inventory[i]?>=?mid:
12????????????????????temp?+=?(inventory[i]?-?mid)
13????????????if?temp?<=?orders:
14????????????????threshold?=?mid
15????????????????high?=?mid?-?1
16????????????else:
17????????????????low?=?mid?+?1
18????????temp?=?0
19????????for?i?in?range(len(inventory)):
20????????????if?inventory[i]?>?threshold:
21????????????????temp?+=?(inventory[i]?-?threshold)
22????????temp?=?orders?-?temp
23????????for?i?in?range(len(inventory)):
24????????????if?inventory[i]?>=?threshold:
25????????????????if?temp?>?0:
26????????????????????#?等差數(shù)列求和公式
27????????????????????res?+=?((inventory[i]?+?threshold)?*?(inventory[i]?-?(threshold)?+?1)?//?2)
28????????????????????temp?-=?1
29????????????????else:
30????????????????????#?等差數(shù)列求和公式
31????????????????????res?+=?((inventory[i]?+?threshold?+?1)?*?(inventory[i]?-?(threshold?+?1)?+?1)?//?2)
32????????return?res?%?max_num

這個是我今天下午剛寫的，前一部分是二分查找的實現(xiàn)，后面是累加求和的過程。

不知道最后一個 for 循環(huán)你看懂了沒？在計算 res的過程中，運(yùn)用到了等差數(shù)列的求和公式，我當(dāng)時在看別人代碼的時候是一臉懵逼的，當(dāng)時想著計算的話不是應(yīng)該有循環(huán)的嗎？為啥沒有循環(huán)呢？沒有循環(huán)怎么計算從 a[i] 到 threshold 呢？突然間恍然大悟，不得不佩服大神。

總結(jié)

現(xiàn)在回過頭來看，這道題的思想已經(jīng)很正常了，但是當(dāng)我在參加 LeetCode 周賽的時候，當(dāng)時心態(tài)都被它給搞崩了。。。

你看提到二分查找算法的話，我想每個人都知道，提及貪心算法，每個人也都有話可說，但是二者結(jié)合起來，就讓很多人摸不著頭腦了。

當(dāng)然，這并不是說我們之前學(xué)的算法知識沒有用，而是我們?nèi)狈σ环N融會貫通的思維，在學(xué)習(xí)的過程中，要學(xué)會舉一反三。

這道題帶給我的不僅僅是知識點(diǎn)的融會貫通，更讓我驚訝的是數(shù)學(xué)知識的使用，沒有刻意的地方，一切是那么的自然。

我們每個人學(xué)數(shù)學(xué)的話也都學(xué)了好多年，但是更多的是用來考試，真正在編程過程的使用時是很少的。

雖然那次周賽我只做了一道題，但是感覺收獲是很大的，開闊了眼界，拓展了思維。

如果你對編程也感興趣的話，歡迎聯(lián)系我，我們共同交流進(jìn)步。

一個人可以走的很快，但一群人可以走的更遠(yuǎn)，共勉。