十大排序之堆排序
十大排序之堆排序(HeapSort)
4.14
簡介
堆排序(英語:Heapsort)是指利用堆這種數(shù)據(jù)結(jié)構(gòu)所設(shè)計(jì)的一種排序算法。
堆排序的時間復(fù)雜度是:O(nlogn) 空間復(fù)雜度:O(1).
說到堆排序就不得不提到完全二叉樹了。什么是完全二叉樹呢?
完全二叉樹定義:
若設(shè)二叉樹的深度為h,除第 h 層外,其它各層 (1~h-1) 的結(jié)點(diǎn)數(shù)都達(dá)到最大個數(shù),第 h 層所有的結(jié)點(diǎn)都連續(xù)集中在最左邊,這就是完全二叉樹。
一顆普通的完全二叉樹:
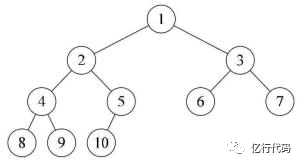
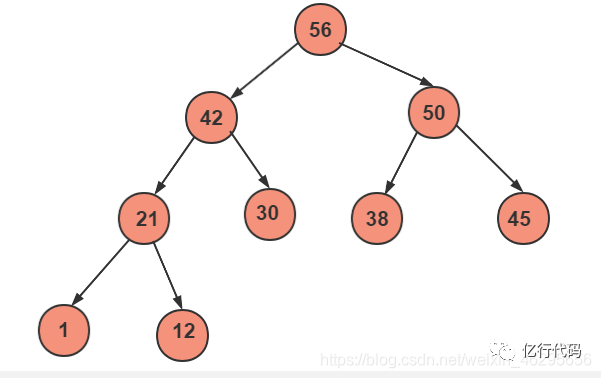
我們把堆又分為大根堆和小根堆,
大根堆:根結(jié)點(diǎn)的鍵值是所有堆結(jié)點(diǎn)鍵值中最大者,在堆排序算法中用于升序排列。
小根堆:根結(jié)點(diǎn)的鍵值是所有堆結(jié)點(diǎn)鍵值中最小者,在堆排序算法中用于降序排列;
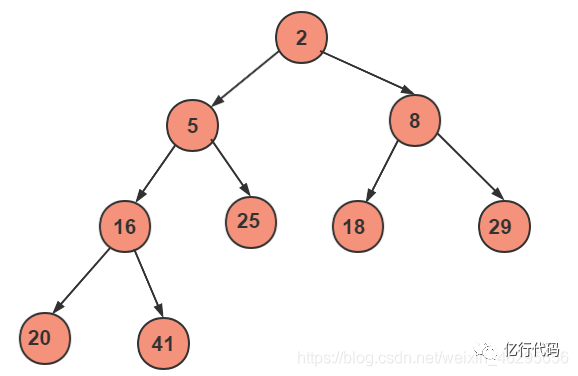
4.14
圖解步驟
利用堆排序的實(shí)現(xiàn)排序的思路也很簡單:
第一步、將待排序數(shù)組構(gòu)建成一個堆(大根堆或者小根堆,一般用大根堆來升序 排序);
第二步、把堆首(最大值)和堆尾互換;取出最大的元素(此時堆個數(shù)減一);
第三步、重新構(gòu)建大根堆;
第四步、重復(fù)第二步,第三步,知道堆的大小為1,完成排序。
圖解:
假設(shè)待排序數(shù)組:1,5,2,12,10,9
假設(shè)我們使用大根堆來排序:
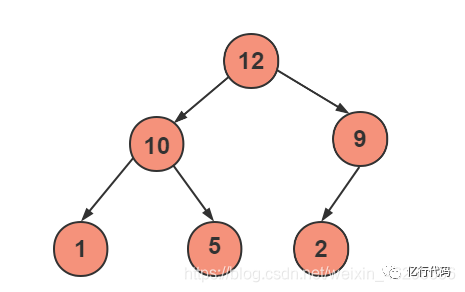
將堆首元素和堆尾元素交換:
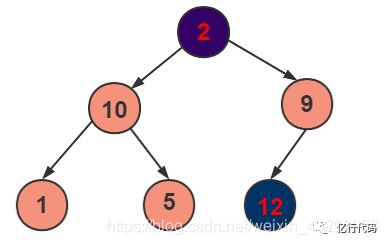
剔除最后一個元素,然后將剩下的元素,重新構(gòu)建成一個堆。
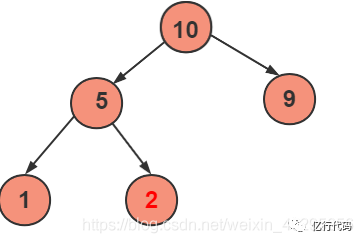
繼續(xù)交換堆首元素和堆尾元素
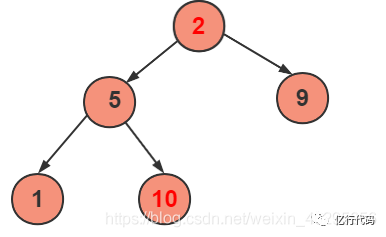
剔除最后一個元素,然后將剩下的元素,重新構(gòu)建成一個堆。
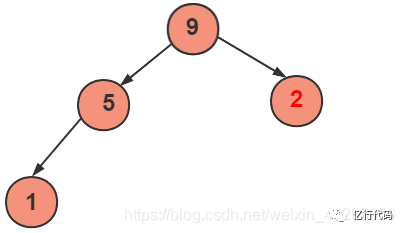
交換:
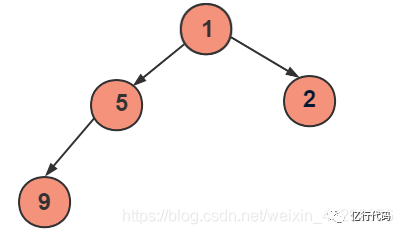
剔除,構(gòu)建堆。

交換,剔除。
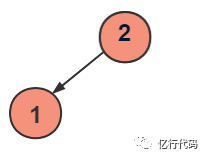
交換,剔除。

最終完成排序:
1 2 5 9 10 12
4.14
代碼實(shí)現(xiàn)
package com.znzz.heapSort;import java.util.Arrays;public class HeapSort {public static void main(String[] args) {int[] arr = {2,4,1,8,20,3,6};new HeapSort().heap_sort(arr, arr.length);System.out.println(Arrays.toString(arr));}/**** @param arr 待排數(shù)組* @param n 數(shù)組元素* @param i 對哪個節(jié)點(diǎn)做heapify*/void heapify(int arr[], int n, int i){if(i >= n){return;}int c1 = 2 * i + 1;int c2 = 2 * i + 2;int max = i;if(c1 < n && arr[c1] > arr[max]){max = c1;}if(c2 < n && arr[c2] > arr[max]){max = c2;}if(max != i){swap(arr,max ,i);heapify(arr,n,max);}}private void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}void build_heap(int arr[], int n){int last_node = n -1;int parent = (last_node -1) /2;int i;for (i = parent; i >= 0; i--) {heapify(arr,n,i);}}void heap_sort(int arr[], int n){build_heap(arr,n);for (int i = n -1; i >= 0 ; i--) {swap(arr,i,0);heapify(arr,i ,0);}}}
小根堆排序(即降序排列)只需要把a(bǔ)rr[c1] > arr[max] 和arr[c2] > arr[max] 中條件改為小于即可。
如果該文章對你有幫助,"再看"和"點(diǎn)贊"是對我最大的鼓勵!
掃二維碼|關(guān)注我們
謝謝觀看

把城市夜晚的喧囂,點(diǎn)出來
▼
