十大經(jīng)典排序算法之希爾排序算法

希爾排序

之前我們講過冒泡排序、選擇排序、插入排序，它們的時(shí)間復(fù)雜度都是 ,比較高，在實(shí)際的場(chǎng)景用應(yīng)用也比較少。

今天我們要講的希爾排序雖然也是插入排序的一種，但是它是插入排序的一個(gè)高效變形，脫離了 的時(shí)間復(fù)雜度深淵。

主要思想

希爾排序的思想簡(jiǎn)單點(diǎn)說就是有跨度的插入排序，這個(gè)跨度會(huì)逐漸變小，直到變?yōu)?1,變?yōu)?1 的時(shí)候也就是我們之前講的簡(jiǎn)單插入排序了。

規(guī)范點(diǎn)的描述就是,選擇一組遞減的整數(shù)作為增量序列，最小的增量必須為 1。

• 先用第一個(gè)增量把數(shù)組分為若干個(gè)子數(shù)組，每個(gè)子數(shù)組中的元素下標(biāo)距離等于增量；
• 然后對(duì)每個(gè)子數(shù)組進(jìn)行簡(jiǎn)單插入排序
• 再使用第二個(gè)增量，然后繼續(xù)同樣的操作，直到增量序列里的增量都使用過一次（增量為 1 時(shí)，其實(shí)就是對(duì)整個(gè)數(shù)組進(jìn)行簡(jiǎn)單插入排序）。

可能你有點(diǎn)疑惑為啥剛開始要進(jìn)行大跨度的插入排序呢？說實(shí)話我剛開始的時(shí)候也覺得怪怪的，舉個(gè)極端的例子幫助你理解下。

假定 ，對(duì)于簡(jiǎn)單的插入排序，如果最小的元素位于最后面的話，那么它就需要和所有的元素比較移動(dòng)一遍，才可以到達(dá)它指定的位置，但是剛開始進(jìn)行大跨度插入排序的時(shí)候，它就可以少比較幾次就可以到達(dá)前面了。

這就是希爾排序的思想。

代碼實(shí)現(xiàn)

#!/usr/bin/python
#?-*-?coding:?utf-8?-*-
from?typing?import?List
import?random



def?shell_sort_original(array:?List[int])?->?None:
????#?增量序列的初始值
????gap?=?len(array)?//?2
????while?gap?>?0:
????????#?對(duì)于?array?進(jìn)行分組，默認(rèn)編號(hào)是?0，?1，?2,?...
????????for?i?in?range(gap):
????????????#?對(duì)于每組進(jìn)行插入排序
????????????for?j?in?range(i+gap,?len(array),?gap):
????????????????temp?=?array[j]
????????????????index?=?j?-?gap
????????????????while?index?>=?0:
????????????????????if?array[index]?>?temp:
????????????????????????array[index+gap]?=?array[index]
????????????????????????index?-=?gap
????????????????????else:
????????????????????????break
????????????????array[index+gap]?=?temp
????????#?增量序列值減小，變?yōu)樵瓉淼?1/2
????????gap?//=?2


if?__name__?==?"__main__":
????min_number,?max_number?=?0,?100
????num?=?10
????array?=?[random.randint(min_number,?max_number)?for?_?in?range(num)]
????print(array)
????shell_sort_original(array)
????print(array)

乍一看，這個(gè)程序一共有四層循環(huán)，是不是覺得這個(gè)程序怎么可能是插入排序的優(yōu)化算法呢？但是這個(gè)確實(shí)是按照希爾排序的思想進(jìn)行寫出來的。

確實(shí)，這個(gè)程序確實(shí)是四層循環(huán)，但是呢一個(gè)程序的時(shí)間復(fù)雜度不能單單看循環(huán)的層數(shù)，更應(yīng)該看的是程序隨著輸入的執(zhí)行次數(shù)。

希爾排序的寫法優(yōu)化

雖然上面的寫法就是完全按照希爾排序的思想來進(jìn)行實(shí)現(xiàn)的，但是呢，寫的不夠簡(jiǎn)潔。

下面帶你看下一個(gè)更常用的寫法：

#!/usr/bin/python
#?-*-?coding:?utf-8?-*-
from?typing?import?List
import?random


def?shell_sort(array:?List[int])?->?None:
????#?增量序列
????gap?=?len(array)?//?2
????while?gap?>?0:
????????for?i?in?range(gap,?len(array)):
????????????temp?=?array[i]
????????????index?=?i?-?gap
????????????while?index?>=?0:
????????????????if?array[index]?>?temp:
????????????????????array[index?+?gap]?=?array[index]
????????????????????index?-=?gap
????????????????else:
????????????????????break
????????????array[index+gap]?=?temp
????????gap?//=?2


if?__name__?==?"__main__":
????min_number,?max_number?=?0,?100
????num?=?10
????array?=?[random.randint(min_number,?max_number)?for?_?in?range(num)]
????print(array)
????shell_sort(array)
????print(array)

這種實(shí)現(xiàn)方法在表面上模糊了對(duì)數(shù)組分組的概念，而是在進(jìn)行插入排序的時(shí)候通過設(shè)置 的變化值為 (之前是 1)，來實(shí)現(xiàn)的。

性能分析

希爾排序的時(shí)間復(fù)雜度不是我們表面認(rèn)為的那樣，一般來說認(rèn)為希爾排序的時(shí)間復(fù)雜度是 ,這個(gè)證明起來比較難。

空間復(fù)雜度的話，希爾排序沒有使用額外的空間，進(jìn)行存儲(chǔ)，是原地排序算法。

希爾排序算法不是穩(wěn)定的排序算法。前面我們也提到過，只要涉及到大跨度的排序算法，一般都不是穩(wěn)定的排序算法。

優(yōu)化

希爾排序的優(yōu)化主要是針對(duì)增量序列的優(yōu)化。增量序列如果取得不好，效率比直接插入排序還要低，下面舉個(gè)例子1：

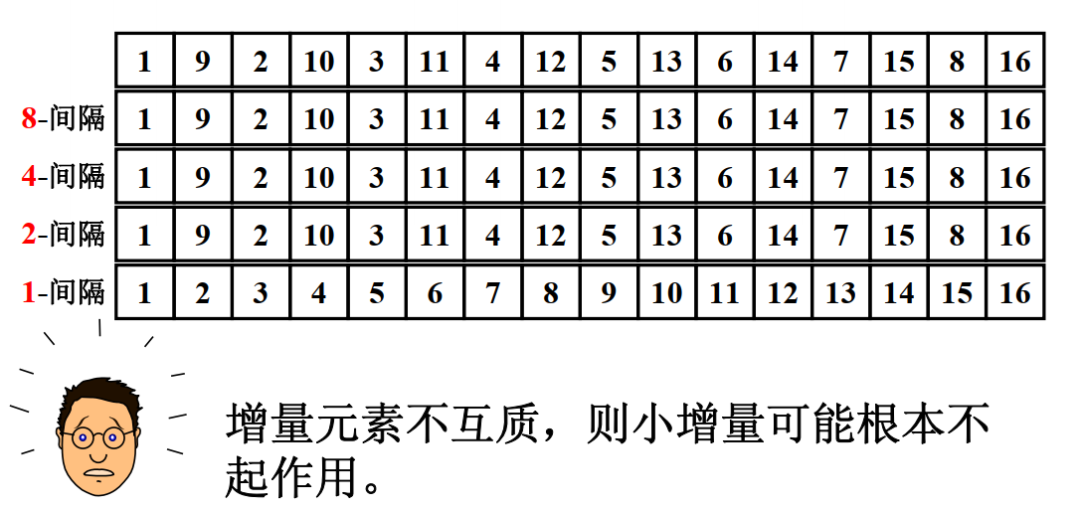
這個(gè)例子就形象說明了這個(gè)問題。

于是呢，人們就研究了一些比較好用的增量序列，比如說Hibbard增量序列、Sedgewick增量序列。

Hibbard增量序列

Hibbard增量序列的取法為

Sedgewick增量序列

Sedgewick增量序列的取法為

總結(jié)

本文主要介紹了希爾排序的思想及其代碼實(shí)現(xiàn)，通過其兩種代碼實(shí)現(xiàn)也可以看到計(jì)算機(jī)的理論和實(shí)現(xiàn)還是不一樣的，在理解理論的同時(shí)還需要多實(shí)踐才能更好的學(xué)習(xí)編程。

一個(gè)人可以走的更快，一群人可以走得更遠(yuǎn)