點擊上方藍(lán)色字體，選擇“置頂或者星標(biāo)”?

二叉樹簡介

二叉樹是由n（n>=0）個結(jié)點（Node）組成的有序集合，集合或者為空，或者是由一個根節(jié)點加上兩棵分別稱為左子樹和右子樹的、互不相交的二叉樹組成。n=0時稱為空二叉樹。二叉樹的五種形態(tài)：

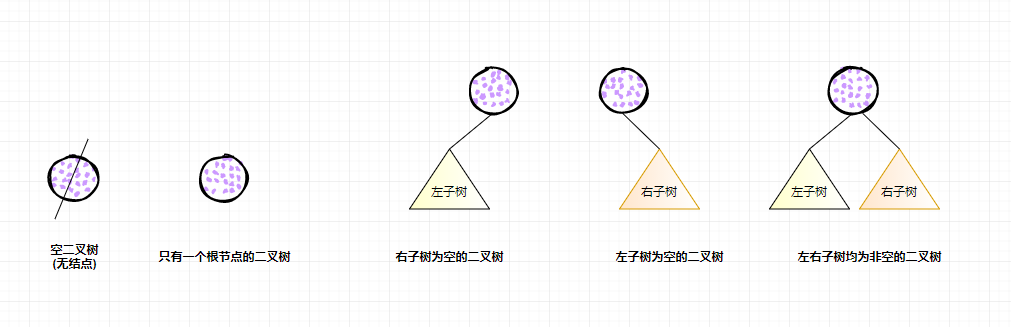
特點

由二叉樹定義以及圖示分析得出二叉樹有以下特點：

• 每個結(jié)點最多有兩顆子樹，所以二叉樹中不存在度大于2的結(jié)點。
• 左子樹和右子樹是有順序的，次序不能任意顛倒。
• 即使樹中某結(jié)點只有一棵子樹，也要區(qū)分它是左子樹還是右子樹。

性質(zhì)

• 在二叉樹的第i層上最多有2i-1 個節(jié)點 。（i>=1）
• 二叉樹中如果深度為k,那么最多有2k-1個節(jié)點。(k>=1）
• n0=n2+1 n0表示度數(shù)為0的節(jié)點數(shù)，n2表示度數(shù)為2的節(jié)點數(shù)。
• 在完全二叉樹中，具有n個節(jié)點的完全二叉樹的深度為[]+1，其中[]是向下取整。
• 若對含 n 個結(jié)點的完全二叉樹從上到下且從左至右進(jìn)行 1 至 n 的編號，則對完全二叉樹中任意一個編號為 i 的結(jié)點有如下特性：

(1) 若 i=1，則該結(jié)點是二叉樹的根，無雙親, 否則，編號為 [i/2] 的結(jié)點為其雙親結(jié)點;
(2) 若 2i>n，則該結(jié)點無左孩子， 否則，編號為 2i 的結(jié)點為其左孩子結(jié)點；
(3) 若 2i+1>n，則該結(jié)點無右孩子結(jié)點， 否則，編號為2i+1 的結(jié)點為其右孩子結(jié)點。

分類

斜二叉樹

只有左子節(jié)點或只有右子節(jié)點的二叉樹稱為斜二叉樹。

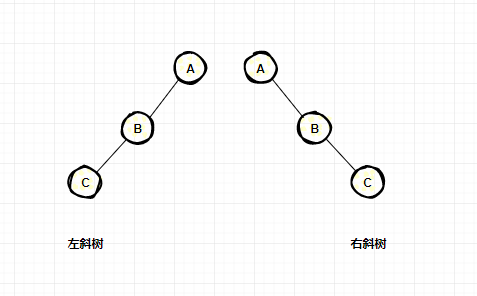
特點：

• 度為1；
• 只有左子節(jié)點或右子節(jié)點；

滿二叉樹

在一棵二叉樹中。如果所有分支結(jié)點都存在左子樹和右子樹，并且所有葉子都在同一層上，這樣的二叉樹稱為滿二叉樹。特點：

• 葉子只能出現(xiàn)在最下一層。出現(xiàn)在其它層就不可能達(dá)成平衡。
• 非葉子結(jié)點的度一定是2。
• 在同樣深度的二叉樹中，滿二叉樹的結(jié)點個數(shù)最多，葉子數(shù)最多。

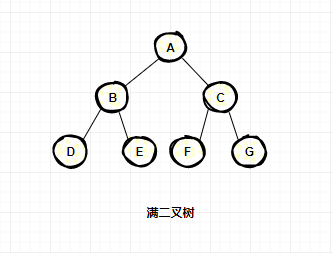
完全二叉樹

對一棵具有n個結(jié)點的二叉樹按層序編號，如果編號為i(1<=i<=n)的結(jié)點與同樣深度的滿二叉樹中編號為i的結(jié)點位置完全相同；

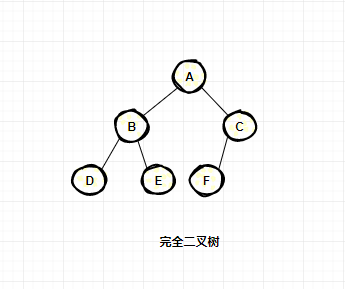
特點：

• 葉子結(jié)點只能出現(xiàn)在最下層和次下層。
• 最下層的葉子結(jié)點集中在樹的左部。
• 倒數(shù)第二層若存在葉子結(jié)點，一定在右部連續(xù)位置。
• 如果結(jié)點度為1，則該結(jié)點只有左孩子，即沒有右子樹。
• 同樣結(jié)點數(shù)目的二叉樹，完全二叉樹深度最小。

注：滿二叉樹一定是完全二叉樹，但反過來不一定成立。

二叉樹遍歷

二叉樹的遍歷是指從根結(jié)點出發(fā)，按照某種次序依次訪問二叉樹中所有節(jié)點，使得每個節(jié)點被訪問依次且僅被訪問一次。二叉樹的遍歷次序不同于線性結(jié)構(gòu)，線性結(jié)構(gòu)最多也就是分為順序、循環(huán)、雙向等簡單的遍歷方式。而樹不存在唯一的后繼節(jié)點，在訪問一個節(jié)點后，下一個被訪問的節(jié)點面臨著不同的選擇，所以我們需要規(guī)范遍歷方式。

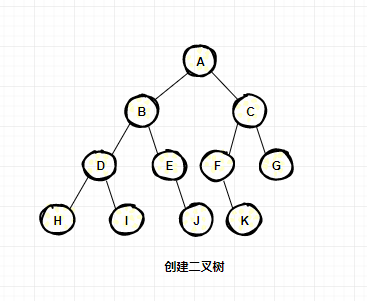
前序遍歷：

定義：先訪問根節(jié)點，然后訪問左子樹，再訪問右子樹；
按照定義遍歷的順序遍歷結(jié)果為：A B D H I E J C F K G
訪問順序如下圖：

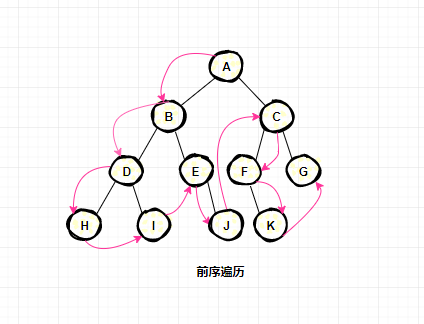
中序遍歷：

定義：先訪問左子樹，再訪問根節(jié)點，最后訪問右子樹；
按照定義遍歷的順序遍歷結(jié)果為：H D I B E J A F K C G
訪問順序如下圖：

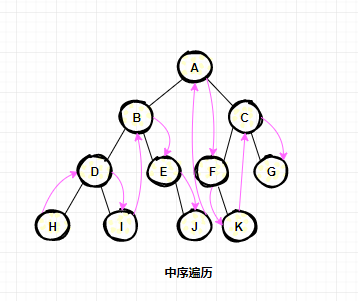
后序遍歷：

定義：先訪問左子樹，再訪問右子樹，最后訪問根節(jié)點；
按照定義遍歷的順序遍歷結(jié)果為：H I D J E B K F G C A
訪問順序如下圖：

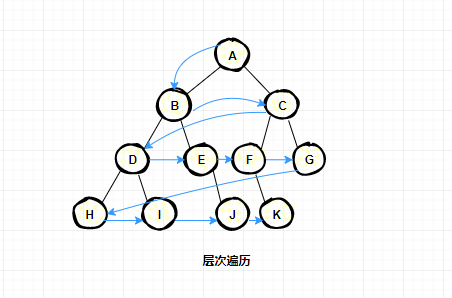
層次遍歷：

定義：逐層的從根節(jié)點開始，每層從左至右遍歷；
按照定義遍歷的順序遍歷結(jié)果為：A B C D E F G H I J K
訪問順序如下圖：

二叉樹存儲結(jié)構(gòu)

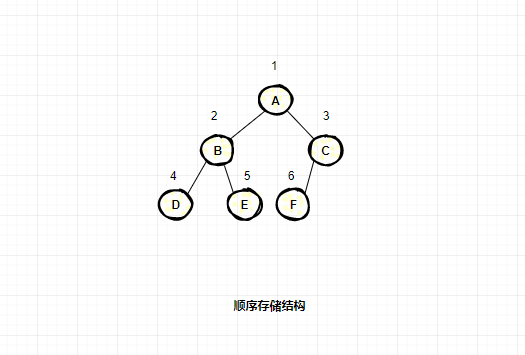
順序存儲結(jié)構(gòu)

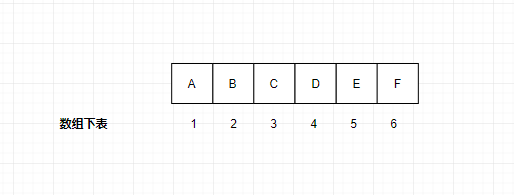
二叉樹的順序存儲，就是用一組連續(xù)的存儲單元存放二叉樹中的結(jié)點。因此，必須把二叉樹的所有結(jié)點安排成為一個恰當(dāng)?shù)男蛄校Y(jié)點在這個序列中的相互位置能反映出結(jié)點之間的邏輯關(guān)系，用編號的方法從樹根起，自上層至下層，每層自左至右地給所有結(jié)點編號,缺點是有可能對存儲空間造成極大的浪費，在最壞的情況下，一個深度為k且只有k個結(jié)點的右單支樹需要2k-1個結(jié)點存儲空間。依據(jù)二叉樹的性質(zhì)，完全二叉樹和滿二叉樹采用順序存儲比較合適，樹中結(jié)點的序號可以唯一地反映出結(jié)點之間的邏輯關(guān)系，這樣既能夠最大可能地節(jié)省存儲空間，又可以利用數(shù)組元素的下標(biāo)值確定結(jié)點在二叉樹中的位置，以及結(jié)點之間的關(guān)系。下圖是完全二叉樹的順序存儲結(jié)構(gòu)：

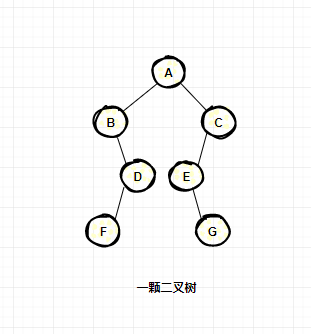
對于一般的二叉樹，如果仍按從上至下和從左到右的順序?qū)渲械慕Y(jié)點順序存儲在一維數(shù)組中，則數(shù)組元素下標(biāo)之間的關(guān)系不能夠反映二叉樹中結(jié)點之間的邏輯關(guān)系，只有增添一些并不存在的空結(jié)點，使之成為一棵完全二叉樹的形式，然后再用一維數(shù)組順序存儲。下面給出了一棵一般二叉樹改造后的完全二叉樹形態(tài)和其順序存儲狀態(tài)示意圖。顯然，這種存儲對于需增加許多空結(jié)點才能將一棵二叉樹改造成為一棵完全二叉樹的存儲時，會造成空間的大量浪費，不宜用順序存儲結(jié)構(gòu)。

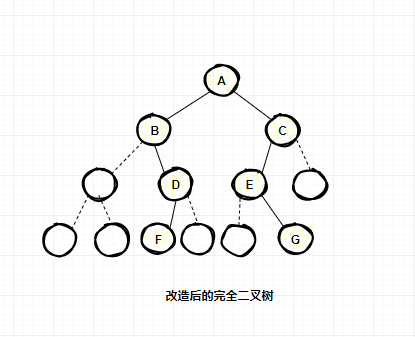
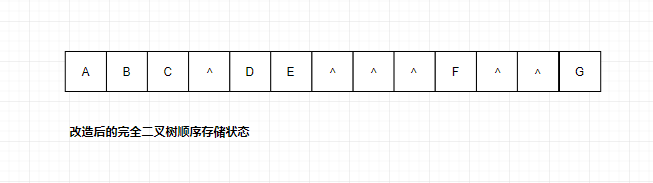
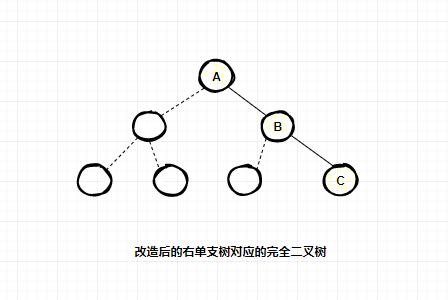
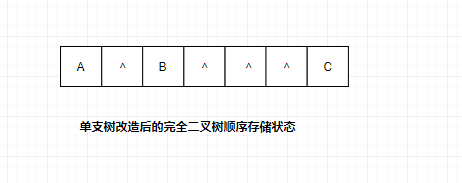
最壞的情況是右單支樹，如圖所示，一棵深度為k的右單支樹，只有k個結(jié)點，卻需分配2k－1個存儲單元。

鏈?zhǔn)酱鎯C構(gòu)

二叉樹的鏈?zhǔn)酱鎯Y(jié)構(gòu)是指，用鏈表來表示一棵二叉樹，即用鏈來指示元素的邏輯關(guān)系。通常的方法是鏈表中每個結(jié)點由三個域組成，數(shù)據(jù)域和左右指針域，左右指針分別用來給出該結(jié)點左孩子和右孩子所在的鏈結(jié)點的存儲地址。其結(jié)點結(jié)構(gòu)為：

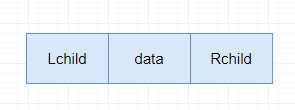
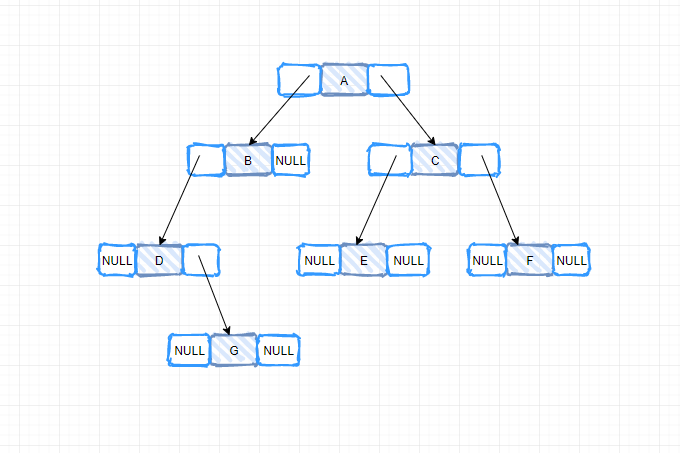
其中，data域存放某結(jié)點的數(shù)據(jù)信息；lchild與rchild分別存放指向左孩子和右孩子的指針，當(dāng)左孩子或右孩子不存在時，相應(yīng)指針域值為空（用符號∧或NULL表示）。利用這樣的結(jié)點結(jié)構(gòu)表示的二叉樹的鏈?zhǔn)酱鎯Y(jié)構(gòu)被稱為二叉鏈表，如圖所示。