本文簡(jiǎn)要介紹快速冪、快速乘等算法，并與取模運(yùn)算進(jìn)行結(jié)合

快速冪

所謂快速冪，指的是快速計(jì)算冪的方法。例如計(jì)算3的23次冪，如果采用樸素的方式一次一次地乘3，需要進(jìn)行22次。其時(shí)間復(fù)雜度為線性時(shí)間。而如果轉(zhuǎn)換思路，我們將指數(shù)的23改為采用二進(jìn)制表示：10111。如下所示，可以看到，變成若干個(gè)乘數(shù)（即下圖的3的1次方、3的2次方、3的4次方、3的16次方）進(jìn)行相乘。其中每個(gè)乘數(shù)是前一個(gè)乘數(shù)的平方。特別地，對(duì)于指數(shù)相應(yīng)二進(jìn)制位為0的乘數(shù)（例如下圖紅框中3的8次方），則在最終計(jì)算過(guò)程中直接跳過(guò)即可。可以看到，快速冪的時(shí)間復(fù)雜度為對(duì)數(shù)時(shí)間

Java版本實(shí)現(xiàn)如下所示

/**
?*?快速冪
?*?@param?base?底數(shù)
?*?@param?exp?指數(shù)
?*?@return
?*/
public?static?long?quickPower(long?base,?long?exp)?{
????//?乘法單位元為1
????long?result?=?1;
????long?temp?=?base;
????while?(exp!=0)?{
????????//?取出指數(shù)在二進(jìn)制下的最后一位
????????long?lastBit?=?exp&1;
????????//?該位不為0,?說(shuō)明最終計(jì)算結(jié)果需要乘上這個(gè)中間乘數(shù)
????????if(?lastBit!=0?)?{
????????????result?*=?temp;
????????}
????????//?更新中間乘數(shù)
????????temp?*=?temp;
????????//?移除指數(shù)在二進(jìn)制下的最后一位
????????exp?>>=?1;
????}
????return?result;
}

模冪運(yùn)算

在快速冪的基礎(chǔ)上，我們來(lái)看下如何進(jìn)行模冪運(yùn)算。即形如“(x^y) mod z”。在進(jìn)一步展開(kāi)前，我們先介紹下模在乘法下的運(yùn)算規(guī)則

//?乘積的模?等于?各乘數(shù)分別取模后求積、并對(duì)積再取一次模
(a·b)?mod?z?=?[(a?mod?z)·(b?mod?z)]?mod?z

這里，我們以（3^23）mod 7 為例進(jìn)行說(shuō)明。結(jié)合快速冪、模運(yùn)算規(guī)則進(jìn)行轉(zhuǎn)換如下所示，可以看到轉(zhuǎn)換后的各乘數(shù)X實(shí)際上是對(duì)前一個(gè)X的平方再取模的結(jié)果，體現(xiàn)在下述代碼的(2)處

這里我們令X1～X4乘積后進(jìn)行取模的結(jié)果為A4，再次運(yùn)用模運(yùn)算規(guī)則進(jìn)行轉(zhuǎn)換。由于X4肯定小于7，故X4 mod 7 可以直接化簡(jiǎn)為X4。同時(shí)令X1～X3乘積后進(jìn)行取模的結(jié)果為A3。可以看到其揭示了我們?cè)诤竺孢M(jìn)行迭代計(jì)算過(guò)程中的遞推公式，體現(xiàn)在下述代碼的(1)處

此時(shí)，我們就可以利用快速冪實(shí)現(xiàn)模冪運(yùn)算，Java實(shí)現(xiàn)如下所示

/**
?*?模冪運(yùn)算
?*?@param?base?底數(shù)
?*?@param?exp?指數(shù)
?*?@param?n?模
?*?@return
?*/
public?static?long?modPower(long?base,?long?exp,?long?n)?{
????//?乘法單位元為1
????long?result?=?1;
????//?即公式中的X1
????long?temp?=?base?%?n;
????while?(exp!=0)?{
????????//?取出指數(shù)在二進(jìn)制下的最后一位
????????long?lastBit?=?exp&1;
????????//?該位不為0,?說(shuō)明最終計(jì)算結(jié)果需要乘上這個(gè)中間乘數(shù)
????????if(?lastBit!=0?)?{
????????????//?此處應(yīng)用迭代計(jì)算過(guò)程的遞推公式
????????????result?=?(result?*?temp)?%?n;??//?(1)
????????}
????????//?更新中間乘數(shù):?對(duì)前一個(gè)乘數(shù)進(jìn)行平方再取模
????????temp?=?(temp?*?temp)?%?n;???//?(2)
????????//?移除指數(shù)在二進(jìn)制下的最后一位
????????exp?>>=?1;
????}
????return?result;
}

快速乘

介紹完快速冪，相應(yīng)的快速乘就簡(jiǎn)單很多了。其基本原理也是類似的，將其中的一個(gè)乘數(shù)按二進(jìn)制進(jìn)行拆分，然后利用分配律將乘法轉(zhuǎn)換為加法。可以看到，一方面，對(duì)于兩個(gè)大數(shù)相乘的場(chǎng)景，快速乘通過(guò)將乘法變?yōu)榧臃ù蟠筇岣咂湓谟?jì)算機(jī)中的運(yùn)算效率；另一方面，對(duì)于大數(shù)的模乘運(yùn)算而言，形如“(x·y) mod z”。借助快速乘可以防止兩個(gè)大數(shù)的乘積直接溢出。典型地，模乘運(yùn)算廣泛存在于RSA計(jì)算當(dāng)中

例如計(jì)算3x23，我們將其中一個(gè)乘數(shù)23改為采用二進(jìn)制表示：10111，然后采用乘法的分配律將其改寫加法。類似地，可以看到各加數(shù)均是前一個(gè)加數(shù)的兩倍

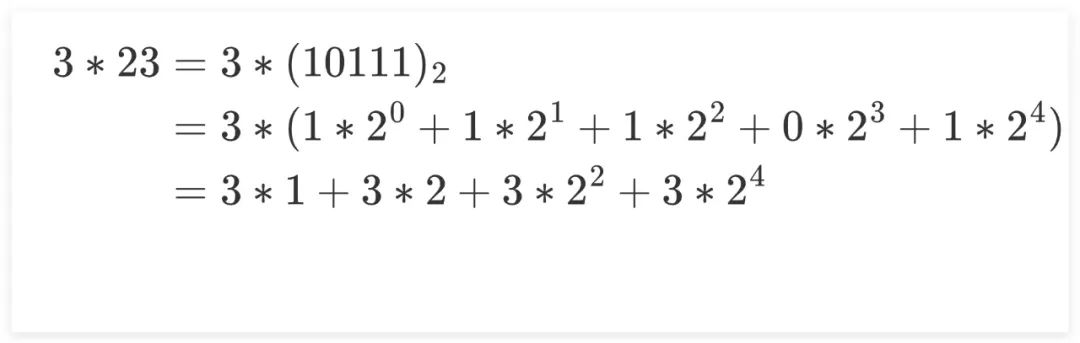
Java實(shí)現(xiàn)如下所示

/**
?*?快速乘
?*?@param?num1?乘數(shù)1
?*?@param?num2?乘數(shù)2
?*?@return
?*/
public?static?long?quickMultiply(long?num1,?long?num2)?{
????//?加法單位元為0
????long?result?=?0;
????long?temp?=?num1;
????while?(num2!=0)?{
????????//?取出num2在二進(jìn)制下的最后一位
????????long?lastBit?=?num2&1;
????????//?該位不為0,?說(shuō)明最終計(jì)算結(jié)果需要加上這個(gè)中間數(shù)
????????if(?lastBit!=0?)?{
????????????result?+=?temp;
????????}
????????//?更新中間數(shù)
????????temp?+=?temp;
????????//?移除指數(shù)在二進(jìn)制下的最后一位
????????num2?>>=?1;
????}
????return?result;
}

模乘運(yùn)算

在快速乘的基礎(chǔ)上，我們來(lái)看下如何進(jìn)行模乘運(yùn)算。即形如“(x·y) mod z”。在進(jìn)一步展開(kāi)前，我們先介紹下模在加法下的運(yùn)算規(guī)則

//?和的模?等于?各數(shù)分別取模后求和、并對(duì)和再取一次模
(a+b)?mod?z?=?[(a?mod?z)+(b?mod?z)]?mod?z

這里，我們以（3x23）mod 7 為例進(jìn)行說(shuō)明。結(jié)合快速乘、模運(yùn)算規(guī)則進(jìn)行轉(zhuǎn)換如下所示，可以看到轉(zhuǎn)換后的各加數(shù)X實(shí)際上是前一個(gè)X的兩倍再取模的結(jié)果，體現(xiàn)在下述代碼的(2)處

這里我們令X1～X4之和進(jìn)行取模的結(jié)果為A4，再次運(yùn)用模運(yùn)算規(guī)則進(jìn)行轉(zhuǎn)換。由于X4肯定小于7，故X4 mod 7 可以直接化簡(jiǎn)為X4。同時(shí)令X1～X3之和進(jìn)行取模的結(jié)果為A3。可以看到其揭示了我們?cè)诤竺孢M(jìn)行迭代計(jì)算過(guò)程中的遞推公式，體現(xiàn)在下述代碼的(1)處

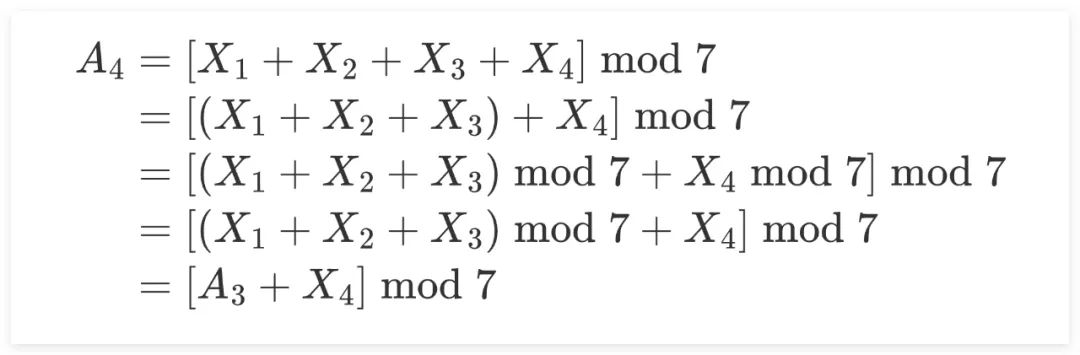
此時(shí)，我們就可以利用快速乘實(shí)現(xiàn)模乘運(yùn)算，Java實(shí)現(xiàn)如下所示

/**
?*?模乘運(yùn)算
?*?@param?num1?乘數(shù)1
?*?@param?num2?乘數(shù)2
?*?@param?n?模
?*?@return
?*/
public?static?long?modMultiply(long?num1,?long?num2,?long?n)?{
????//?加法單位元為0
????long?result?=?0;
????//?即公式中的X1
????long?temp?=?num1?%?n;
????while?(num2!=0)?{
????????//?取出num2在二進(jìn)制下的最后一位
????????long?lastBit?=?num2&1;
????????//?該位不為0,?說(shuō)明最終計(jì)算結(jié)果需要加上這個(gè)中間數(shù)
????????if(?lastBit!=0?)?{
????????????//?此處應(yīng)用迭代計(jì)算過(guò)程遞推公式
????????????result?=?(result?+?temp)?%?n;???//（1）
????????}
????????//?更新中間數(shù):?對(duì)前一個(gè)數(shù)翻倍再取模
????????temp?=?(temp+temp)?%?n;?//?(2)
????????//?移除指數(shù)在二進(jìn)制下的最后一位
????????num2?>>=?1;
????}
????return?result;
}

矩陣快速冪

前面我們提到了快速冪，故這里就矩陣的快速冪作一下補(bǔ)充說(shuō)明。首先，對(duì)于矩陣形式的快速冪而言，其與普通的快速冪在基本原理上沒(méi)有差別，都是將指數(shù)部分轉(zhuǎn)換為二進(jìn)制進(jìn)行處理。但需要注意的是對(duì)于矩陣乘法而言，其乘法的單位元是單位矩陣。這里給出基于Groovy的矩陣快速冪實(shí)現(xiàn)。借助于Groovy的運(yùn)算符重載特性，可以很方便的進(jìn)行矩陣乘法運(yùn)算

class?Matrix?{
????/**
?????*?矩陣階數(shù)
?????*/
????int?n

????/**
?????*?矩陣數(shù)據(jù)
?????*/
????List>?mat

????Matrix(List>?initValue)?{
????????this.n?=?initValue.size()
????????//?初始化矩陣數(shù)據(jù)
????????this.mat?=?initValue
????}

????/**
?????*?重載?*?乘法運(yùn)算符,?實(shí)現(xiàn)矩陣乘法
?????*?@param?other
?????*?@return
?????*/
????Matrix?multiply(Matrix?other)?{
????????List>?resultData?=?[]
????????for(?row?in?0..????????????List?rowList?=?[]
????????????for(?col?in?0..????????????????def?num?=?0l
????????????????(0..
????????????????????num?+=?this.mat[row][i]?*?other.mat[i][col]
????????????????}
????????????????rowList?<????????????}
????????????resultData?<????????}
????????return?new?Matrix(resultData)
????}

????/**
?????*?獲取n階單位矩陣
?????*?@param?n?階數(shù)
?????*?@return
?????*/
????static?Matrix?identityMat(int?n)?{
????????List>?resultData?=?new?ArrayList<>(n)
????????(0..
????????????List?subList?=?new?ArrayList<>(?Collections.nCopies(n,0l)?)
????????????subList[i]?=?1l
????????????resultData?<????????}
????????return?new?Matrix(resultData)
????}

????/**
?????*?矩陣快速冪
?????*?@param?matrix?n階方陣
?????*?@param?exp?指數(shù)
?????*?@return
?????*/
????static?Matrix?quickMatrixPower(Matrix?matrix,?long?exp)?{
????????//?矩陣乘法單位元:?n階單位矩陣
????????Matrix?result?=?Matrix.identityMat(?matrix.n?)
????????Matrix?temp?=?matrix
????????while?(exp!=0)?{
????????????//?取出指數(shù)在二進(jìn)制下的最后一位
????????????long?lastBit?=?exp&1
????????????//?該位不為0,?說(shuō)明最終計(jì)算結(jié)果需要乘上這個(gè)中間乘數(shù)
????????????if(?lastBit!=0?)?{
????????????????result?=?result?*?temp
????????????}
????????????//?更新中間乘數(shù)
????????????temp?=?temp?*?temp
????????????//?移除指數(shù)在二進(jìn)制下的最后一位
????????????exp?>>=?1
????????}
????????return?result
????}
}