【統(tǒng)計學(xué)習(xí)方法】第1章 統(tǒng)計學(xué)習(xí)方法概論（三）習(xí)題

題目：

說明伯努利模型的極大似然估計以及貝葉斯估計中的統(tǒng)計學(xué)習(xí)方法三要素。伯努利模型是定義在取值為0與1的隨機變量上的概率分布。假設(shè)觀測到伯努利模型n次獨立的數(shù)據(jù)生成結(jié)果，其中k次的結(jié)果為1，這時可以用極大似然估計或貝葉斯估計來估計結(jié)果為1的概率。

解答：

1 極大似然估計

模型：

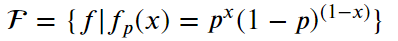
策略：最大似然估計

算法：

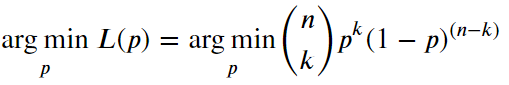
2 貝葉斯估計

模型：

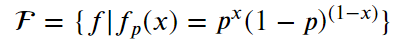
策略：求參數(shù)期望

算法：

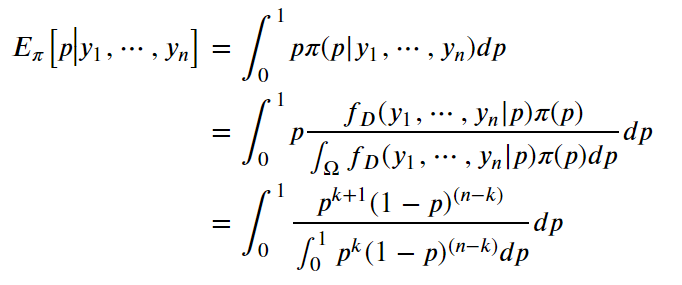
• 伯努利模型的極大似然估計：
  

定義P(Y=1)概率為p，可以得到似然函數(shù)：

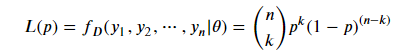
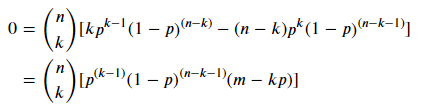
可以得到p的值為0，1，k/n

• 伯努利模型的貝葉斯估計

定義??的概率為??,??在[0, 1]之間的的取值是等概率的，因此先驗概率密度??，可以得到似然函數(shù)，

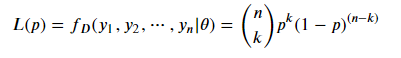
根據(jù)似然函數(shù)和先驗概率密度函數(shù)，可以求解??的條件概率密度函數(shù)：

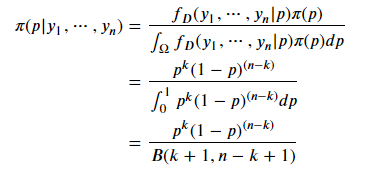
所以??的期望為：

所以，

??

題目：

通過經(jīng)驗風(fēng)險模型最小化推導(dǎo)極大似然估計。證明模型是條件概率分布，當(dāng)損失函數(shù)是對數(shù)損失函數(shù)時，經(jīng)驗風(fēng)險最小化等價于極大似然估計。

解答：

假設(shè)模型的條件概率分布是??,現(xiàn)推導(dǎo)當(dāng)損失函數(shù)是對數(shù)損失函數(shù)時，極大似然估計等價于經(jīng)驗風(fēng)險最小化。

極大似然估計的似然函數(shù)為：

??

兩邊取對數(shù)，

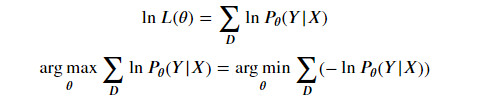
反之，經(jīng)驗風(fēng)險最小化等價于極大似然估計，可通過經(jīng)驗風(fēng)險最小化推導(dǎo)極大似然估計。

掃碼關(guān)注