大香蕉俺也去在线,国产女人在线播放,操韩国美女,在线天堂国产产,国产无码在线影院,大吊操逼了,国产中文字幕第一页,久99在线观看

點(diǎn)擊上方“公眾號(hào)”可訂閱哦！

“如果我較早地了解這個(gè)公眾號(hào)，也許我將有足夠的時(shí)間來制定大統(tǒng)一理論。”

Albert Einstein

本章主要簡(jiǎn)述統(tǒng)計(jì)學(xué)習(xí)方法的一些基本概念

●

統(tǒng)計(jì)學(xué)習(xí)

統(tǒng)計(jì)學(xué)習(xí)

統(tǒng)計(jì)學(xué)習(xí)是關(guān)于計(jì)算機(jī)基于數(shù)據(jù)構(gòu)建概率統(tǒng)計(jì)模型，并運(yùn)用模型對(duì)數(shù)據(jù)進(jìn)行預(yù)測(cè)與分析的一門學(xué)科。統(tǒng)計(jì)學(xué)習(xí)包括監(jiān)督學(xué)習(xí)、非監(jiān)督學(xué)習(xí)、半監(jiān)督學(xué)習(xí)和強(qiáng)化學(xué)習(xí)。

統(tǒng)計(jì)學(xué)習(xí)方法的步驟

得到一個(gè)有限的數(shù)據(jù)集合
確定所包含所有可能的模型的假設(shè)空間，即學(xué)習(xí)模型的集合
確定模型選擇的準(zhǔn)則，即學(xué)習(xí)的策略
實(shí)現(xiàn)求解最優(yōu)模型的算法，即學(xué)習(xí)的算法
通過學(xué)習(xí)方法選擇最優(yōu)模型
利用學(xué)習(xí)的最優(yōu)模型對(duì)新數(shù)據(jù)進(jìn)行預(yù)測(cè)或者分析

本書以介紹統(tǒng)計(jì)學(xué)習(xí)方法為主，特別是監(jiān)督學(xué)習(xí)方法，主要包括用于分類、標(biāo)注與回歸問題的方法。

●

監(jiān)督學(xué)習(xí)

1 監(jiān)督學(xué)習(xí)的任務(wù)是學(xué)習(xí)一個(gè)模型，使模型能夠?qū)θ我饨o定的輸入，對(duì)其相應(yīng)的輸出做一個(gè)好的預(yù)測(cè)。

在監(jiān)督學(xué)習(xí)過程中，將輸入與輸出看作是定義在輸入（特征）空間與輸出空間上的隨機(jī)變量的取值。

輸入實(shí)例記作

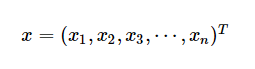
監(jiān)督學(xué)習(xí)從訓(xùn)練數(shù)據(jù)集合中學(xué)習(xí)模型，對(duì)測(cè)試數(shù)據(jù)進(jìn)行預(yù)測(cè)，訓(xùn)練數(shù)據(jù)由輸入與輸出對(duì)組成，訓(xùn)練集通常表示為：

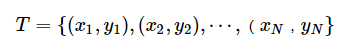
監(jiān)督學(xué)習(xí)的模型可以是概率模型或非概率模型，由條件概率分布P(Y|X)或決策函數(shù)Y=f(X)，表示，隨具體學(xué)習(xí)方法而定。

2?問題的形式化

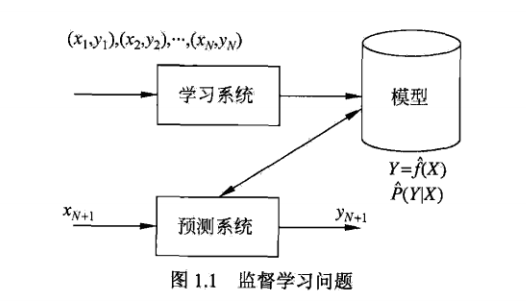
在學(xué)習(xí)過程中，學(xué)習(xí)系統(tǒng)（也就是學(xué)習(xí)算法）試圖通過訓(xùn)練數(shù)據(jù)集中的樣本帶來的信息學(xué)習(xí)模型。具體地說，對(duì)輸入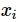，一個(gè)具體的模型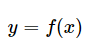可以產(chǎn)生一個(gè)輸出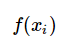，而訓(xùn)練數(shù)據(jù)集中對(duì)應(yīng)的輸出是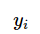，如果這個(gè)模型有很好的預(yù)測(cè)能力，訓(xùn)練樣本輸出的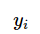和模型預(yù)輸出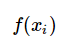之間的差就應(yīng)該足夠小。學(xué)習(xí)系統(tǒng)通過不斷的嘗試，選取最好的模型，以便對(duì)訓(xùn)練數(shù)據(jù)集有足夠好的預(yù)測(cè)，同時(shí)對(duì)未知的測(cè)試數(shù)據(jù)集的預(yù)測(cè)也有盡可能好的推廣。

●

統(tǒng)計(jì)學(xué)習(xí)三要素

統(tǒng)計(jì)學(xué)習(xí)方法都是由模型、策略和算法構(gòu)成的，即統(tǒng)計(jì)學(xué)習(xí)方法由三要素構(gòu)成，可以簡(jiǎn)單的表示為：

方法 = 模型?+ 策略?+ 算法

1 模型

統(tǒng)計(jì)學(xué)習(xí)首要考慮的問題是學(xué)習(xí)什么樣的模型。在監(jiān)督學(xué)習(xí)過程中，模型就是所要學(xué)習(xí)的條件概率分布或決策函數(shù)。

? $\digamma = \left \{ f|Y =f(X) \right \}$ ? 或?? $\digamma = \left \{ P|P (Y|X) \right \}$ ?

2 策略

有了模型的假設(shè)空間，統(tǒng)計(jì)學(xué)習(xí)接著需要考慮的是按照什么樣的準(zhǔn)則學(xué)習(xí)或選擇最優(yōu)的模型。

1）0-1損失函數(shù)

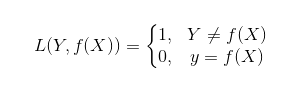
2）平方損失函數(shù)

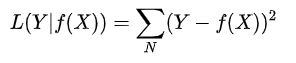
3）絕對(duì)損失函數(shù)

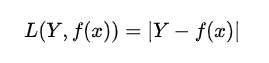
4）對(duì)數(shù)

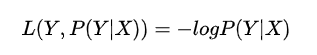
損失函數(shù)值越小，模型就越好。

經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化（ERM）的策略認(rèn)為，經(jīng)驗(yàn)風(fēng)險(xiǎn)最小的模型就是最優(yōu)模型。

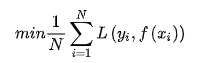
當(dāng)樣本容量足夠大時(shí)，經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化能夠保證有很好的學(xué)習(xí)效果，在現(xiàn)實(shí)中被廣泛采用，比如，極大似然估計(jì)就是經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化的一個(gè)例子。但是當(dāng)樣本容量很小時(shí)，經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化的學(xué)習(xí)效果就未必好，會(huì)產(chǎn)生過擬合現(xiàn)象。

結(jié)構(gòu)風(fēng)險(xiǎn)最小化（SRM）是為了防止過擬合而提出來的策略。結(jié)構(gòu)風(fēng)險(xiǎn)最小化等價(jià)于正則化。結(jié)構(gòu)風(fēng)險(xiǎn)在經(jīng)驗(yàn)風(fēng)險(xiǎn)上加上表示模型復(fù)雜程度的正則化項(xiàng)。

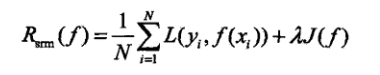
3 算法

算法是指學(xué)習(xí)模型的具體計(jì)算方法。統(tǒng)計(jì)學(xué)習(xí)基于訓(xùn)練數(shù)據(jù)集，根據(jù)學(xué)習(xí)策略，從假設(shè)空間中選擇最優(yōu)模型，最后需要考慮用什么樣的計(jì)算方法求解最優(yōu)模型。

●

模型評(píng)估與模型選擇

1 訓(xùn)練誤差與測(cè)試誤差

統(tǒng)計(jì)學(xué)習(xí)的目的是使學(xué)到的模型不僅對(duì)已知數(shù)據(jù)而且對(duì)未知的數(shù)據(jù)都有較好的預(yù)測(cè)能力。不同的學(xué)習(xí)方法給出不同的模型，當(dāng)損失函數(shù)給定時(shí)，基于損失函數(shù)的模型的訓(xùn)練誤差和模型的預(yù)測(cè)誤差就自然成為學(xué)習(xí)方法的評(píng)估標(biāo)準(zhǔn)。

訓(xùn)練數(shù)據(jù)平均損失：

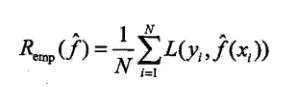
測(cè)試數(shù)據(jù)平均損失：

通常將學(xué)習(xí)方法對(duì)未知數(shù)據(jù)的預(yù)測(cè)能力稱為泛化能力。

2 過擬合與模型選擇

當(dāng)假設(shè)空間含有不同復(fù)雜度的模型時(shí)，就要面臨模型選擇的問題。如果意味追求提高對(duì)訓(xùn)練數(shù)據(jù)的預(yù)測(cè)能力，所選擇的復(fù)雜度則往往會(huì)比真模型更高。這種現(xiàn)象稱為過擬合。

3 例：1.1 使用最小二乘法擬合曲線

假定給定一個(gè)訓(xùn)練數(shù)據(jù)集：

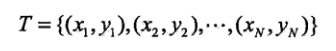
多項(xiàng)式函數(shù)擬合的任務(wù)是假定給定數(shù)據(jù)由M次多項(xiàng)式函數(shù)生成，，選擇最有可能產(chǎn)生這些數(shù)據(jù)的M次多項(xiàng)式函數(shù)，即在M次多項(xiàng)式中選擇一個(gè)對(duì)已知數(shù)據(jù)以及未知數(shù)據(jù)都有很好預(yù)測(cè)能力的函數(shù)。

設(shè)M次多項(xiàng)式為：

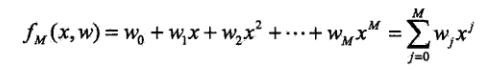
解決這一問題，首先確定模型的復(fù)雜度，即確定多項(xiàng)式的次數(shù)；然后在給定模型復(fù)雜度下，按照經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化的策略，求解參數(shù)，即多項(xiàng)式的次數(shù)。具體的策略：

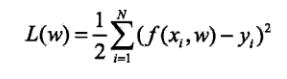
對(duì)w進(jìn)行求導(dǎo)，

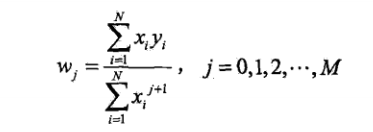
于是求得多項(xiàng)式參數(shù)w。

代碼實(shí)現(xiàn)：

import numpy as npimport scipy as spfrom scipy.optimize import leastsqimport matplotlib.pyplot as plt%matplotlib inline

# 目標(biāo)函數(shù)def real_func(x):    return np.sin(2*np.pi*x)
# 多項(xiàng)式def fit_func(p, x):    f = np.poly1d(p)    return f(x)
# 殘差def residuals_func(p, x, y):    ret = fit_func(p, x) - y    return ret
??# 十個(gè)點(diǎn)x = np.linspace(0, 1, 10)x_points = np.linspace(0, 1, 1000)# 加上正態(tài)分布噪音的目標(biāo)函數(shù)的值y_ = real_func(x)y = [np.random.normal(0, 0.1) + y1 for y1 in y_]
def fitting(M=0):    """    M    為 多項(xiàng)式的次數(shù)    """    # 隨機(jī)初始化多項(xiàng)式參數(shù)    p_init = np.random.rand(M + 1)    # 最小二乘法    p_lsq = leastsq(residuals_func, p_init, args=(x, y))    print('Fitting Parameters:', p_lsq[0])
    # 可視化    plt.plot(x_points, real_func(x_points), label='real')    plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')    plt.plot(x, y, 'bo', label='noise')    plt.legend()    return p_lsq

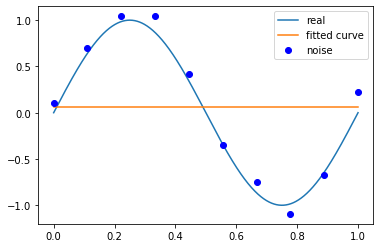
當(dāng)M為0時(shí)，

p_lsq_0 = fitting(M=0)
# outputFitting Parameters: [0.06692556]

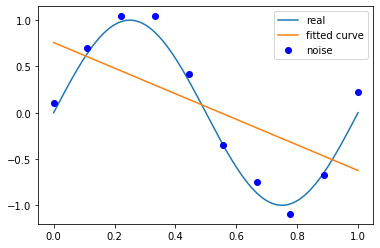
當(dāng)M為1時(shí)，

p_lsq_1 = fitting(M=1)
# outputFitting Parameters: [-1.38229915  0.75807514]

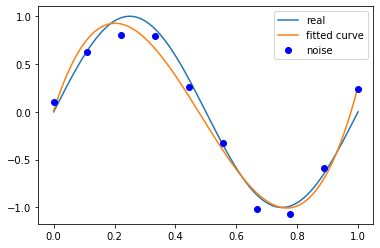
當(dāng)M為3時(shí)，

p_lsq_3 = fitting(M=3)
# outputFitting Parameters: [ 2.14584386e+01 -3.11545570e+01  9.94538545e+00  1.16742107e-02]

當(dāng)M為9時(shí)，

p_lsq_9 = fitting(M=9)
# outputFitting Parameters: [ 2.29442861e+04 -1.03205713e+05  1.95175642e+05 -2.01717066e+05  1.23851279e+05 -4.58498524e+04  9.86820576e+03 -1.12115742e+03  5.45133826e+01  1.05484073e-01]

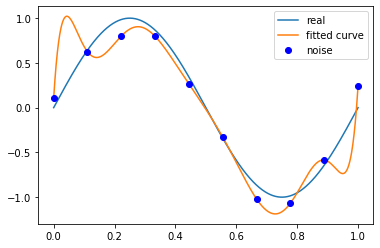
總結(jié)，結(jié)合M=0，1，3，9時(shí)多項(xiàng)式函數(shù)擬合的情況。如果，M為0，多項(xiàng)式曲線是一個(gè)常數(shù)，數(shù)據(jù)擬合效果很差。如果M為1，多項(xiàng)式曲線是一條直線，數(shù)據(jù)擬合效果也很差。相反，如果M為9，多項(xiàng)式曲線通過每一個(gè)數(shù)據(jù)點(diǎn)，訓(xùn)練誤差為0。從對(duì)給定的數(shù)據(jù)擬合的角度來說，效果是最好的。但是，因?yàn)橛?xùn)練數(shù)據(jù)本身存在噪聲，這種擬合的曲線對(duì)未知數(shù)據(jù)的預(yù)測(cè)能力往往不是最好的，在實(shí)際學(xué)習(xí)中并不可取。這時(shí)，過擬合現(xiàn)象就會(huì)發(fā)生。

當(dāng)M為3時(shí)，多項(xiàng)式曲線對(duì)數(shù)據(jù)擬合效果足夠好，模型也比較簡(jiǎn)單，是一個(gè)較好的選擇。

?END

掃碼關(guān)注

微信號(hào)｜sdxx_rmbj

【統(tǒng)計(jì)學(xué)習(xí)方法】 第1章 統(tǒng)計(jì)學(xué)習(xí)方法概論（一）

【統(tǒng)計(jì)學(xué)習(xí)方法】第1章統(tǒng)計(jì)學(xué)習(xí)方法概論（一）