【機器學習基礎(chǔ)】常見二分類損失函數(shù)、距離度量的Python實現(xiàn)
本文用Python實現(xiàn)了常見的幾種距離度量、二分類損失函數(shù)。
設(shè)和為兩個向量,求它們之間的距離。
這里用Numpy實現(xiàn),設(shè)和為ndarray ,它們的shape都是(N,)
為所求的距離,是個浮點數(shù)(float)。
import?numpy?as?np
1.歐氏距離(Euclidean distance)
歐幾里得度量(euclidean metric)(也稱歐氏距離)是一個通常采用的距離定義,指在m維空間中兩個點之間的真實距離,或者向量的自然長度(即該點到原點的距離)。在二維和三維空間中的歐氏距離就是兩點之間的實際距離。
def?euclidean(x,?y):
????return?np.sqrt(np.sum((x?-?y)**2))
2.曼哈頓距離(Manhattan distance)
想象你在曼哈頓要從一個十字路口開車到另外一個十字路口,駕駛距離是兩點間的直線距離嗎?顯然不是,除非你能穿越大樓。實際駕駛距離就是這個“曼哈頓距離”。而這也是曼哈頓距離名稱的來源, 曼哈頓距離也稱為城市街區(qū)距離(City Block distance)。
def?manhattan(x,?y):
????return?np.sum(np.abs(x?-?y))
3.切比雪夫距離(Chebyshev distance)
在數(shù)學中,切比雪夫距離(Chebyshev distance)或是L∞度量,是向量空間中的一種度量,二個點之間的距離定義是其各坐標數(shù)值差絕對值的最大值。以數(shù)學的觀點來看,切比雪夫距離是由一致范數(shù)(uniform norm)(或稱為上確界范數(shù))所衍生的度量,也是超凸度量(injective metric space)的一種。
def?chebyshev(x,?y):
????return?np.max(np.abs(x?-?y))
4.閔可夫斯基距離(Minkowski distance)
閔氏空間指狹義相對論中由一個時間維和三個空間維組成的時空,為俄裔德國數(shù)學家閔可夫斯基(H.Minkowski,1864-1909)最先表述。他的平坦空間(即假設(shè)沒有重力,曲率為零的空間)的概念以及表示為特殊距離量的幾何學是與狹義相對論的要求相一致的。閔可夫斯基空間不同于牛頓力學的平坦空間。
def?minkowski(x,?y,?p):
????return?np.sum(np.abs(x?-?y)?**?p)?**?(1?/?p)
5.漢明距離(Hamming distance)
漢明距離是使用在數(shù)據(jù)傳輸差錯控制編碼里面的,漢明距離是一個概念,它表示兩個(相同長度)字對應(yīng)位不同的數(shù)量,我們以表示兩個字,之間的漢明距離。對兩個字符串進行異或運算,并統(tǒng)計結(jié)果為1的個數(shù),那么這個數(shù)就是漢明距離。
def?hamming(x,?y):
????return?np.sum(x?!=?y)?/?len(x)6.二分類損失函數(shù)
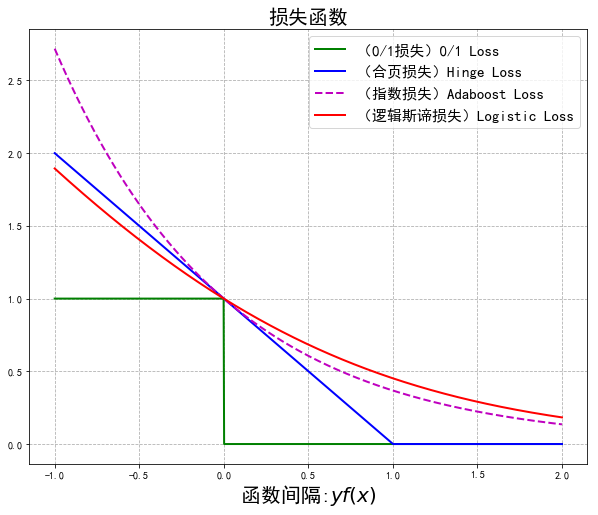
在二分類的監(jiān)督學習中,支持向量機、邏輯斯諦回歸與最大熵模型、提升方法各自使用合頁損失函數(shù)、邏輯斯諦損失函數(shù)、指數(shù)損失函數(shù),分別寫為:
這 3 種損失函數(shù)都是 0-1 損失函數(shù)的上界,具有相似的形狀。(見下圖,由代碼生成)
import?numpy?as?np
import?math
import?matplotlib.pyplot?as?plt
plt.rcParams['font.sans-serif']?=?['SimHei']
plt.rcParams['axes.unicode_minus']?=?False
plt.figure(figsize=(10,8))
x?=?np.linspace(start=-1,?stop=2,?num=1001,?dtype=np.float)
logi?=?np.log(1?+?np.exp(-x))?/?math.log(2)
boost?=?np.exp(-x)
y_01?=?x?0
y_hinge?=?1.0?-?x
y_hinge[y_hinge?0]?=?0
plt.plot(x,?y_01,?'g-',?mec='k',?label='(0/1損失)0/1?Loss',?lw=2)
plt.plot(x,?y_hinge,?'b-',?mec='k',?label='(合頁損失)Hinge?Loss',?lw=2)
plt.plot(x,?boost,?'m--',?mec='k',?label='(指數(shù)損失)Adaboost?Loss',?lw=2)
plt.plot(x,?logi,?'r-',?mec='k',?label='(邏輯斯諦損失)Logistic?Loss',?lw=2)
plt.grid(True,?ls='--')
plt.legend(loc='upper?right',fontsize=15)
plt.xlabel('函數(shù)間隔:$yf(x)$',fontsize=20)
plt.title('損失函數(shù)',fontsize=20)
plt.show()
總結(jié)
本文用Python實現(xiàn)了常見的幾種距離度量、損失函數(shù),歡迎收藏!
推薦閱讀: Pandas數(shù)據(jù)可視化原來也這么厲害 Pandas向量化字符串操作 畫圖神器pyecharts-旭日圖 刷爆網(wǎng)絡(luò)的動態(tài)條形圖,3行Python代碼就能搞定 Python中讀取圖片的6種方式 2020年11月國內(nèi)大數(shù)據(jù)競賽信息-獎池5000萬 Python字典詳解-超級完整版 刷爆網(wǎng)絡(luò)的動態(tài)條形圖,3行Python代碼就能搞定 一個有意思還有用的Python包-漢字轉(zhuǎn)換拼音 ↓內(nèi)推、交流加小編↓ ↓掃描二維碼關(guān)注本號↓