（附代碼）總結(jié) | 卷積網(wǎng)絡(luò)壓縮方法

鏈接 |?https://www.zhihu.com/people/tang-fen-44-49

01

一般地，行階梯型矩陣的秩等于其“臺(tái)階數(shù)”-非零行的行數(shù)。

給定權(quán)重矩陣，若能將其表示為若干個(gè)低秩矩陣的組合，即??, 其中??為低秩矩陣，其秩為??, 并滿足??，則其每一個(gè)低秩矩陣都可分解為小規(guī)模矩陣的乘積，??，其中?，??。當(dāng)??取值很小時(shí)，便能大幅降低總體的存儲(chǔ)和計(jì)算開銷。

1.1，總結(jié)

02

2.1，總結(jié)

03

標(biāo)量量化算法基本思路是，對(duì)于每一個(gè)權(quán)重矩陣??，首先將其轉(zhuǎn)化為向量形式：??。之后對(duì)該權(quán)重向量的元素進(jìn)行??個(gè)簇的聚類，這可借助于經(jīng)典的 k-均值（k-means）聚類算法快速完成：

這樣，只需將??個(gè)聚類中心（??，標(biāo)量）存儲(chǔ)在碼本中，而原權(quán)重矩陣則只負(fù)責(zé)記錄各自聚類中心在碼本中索引。如果不考慮碼本的存儲(chǔ)開銷，該算法能將存儲(chǔ)空間減少為原來的??。基于??均值算法的標(biāo)量量化在很多應(yīng)用中非常有效。參數(shù)量化與碼本微調(diào)過程圖如下：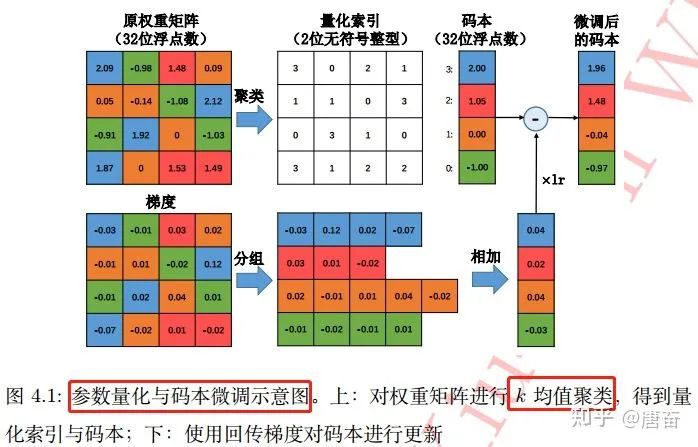

3.1，總結(jié)

04

def residual_unit(data, num_filter, stride, dim_match, num_bits=1):    """殘差塊 Residual Block 定義    """    bnAct1 = bnn.BatchNorm(data=data, num_bits=num_bits)    conv1 = bnn.Convolution(data=bnAct1, num_filter=num_filter, kernel=(3, 3), stride=stride, pad=(1, 1))    convBn1 = bnn.BatchNorm(data=conv1, num_bits=num_bits)    conv2 = bnn.Convolution(data=convBn1, num_filter=num_filter, kernel=(3, 3), stride=(1, 1), pad=(1, 1))    if dim_match:        shortcut = data    else:        shortcut = bnn.Convolution(data=bnAct1, num_filter=num_filter, kernel=(3, 3), stride=stride, pad=(1, 1))    return conv2 + shortcut

4.1，二值網(wǎng)絡(luò)的梯度下降

• 利用決定化方式（sign(x)函數(shù)）把 Weight 量化為?+1/-1, 以0為閾值
• 利用量化后的 Weight (只有+1/-1)來計(jì)算前向傳播，由二值權(quán)重與輸入進(jìn)行卷積運(yùn)算（實(shí)際上只涉及加法），獲得卷積層輸出。
• 反向傳播?Backward Pass:
• 把梯度更新到浮點(diǎn)的 Weight 上（根據(jù)放松后的符號(hào)函數(shù)，計(jì)算相應(yīng)梯度值，并根據(jù)該梯度的值對(duì)單精度的權(quán)重進(jìn)行參數(shù)更新）
• 訓(xùn)練結(jié)束：把 Weight 永久性轉(zhuǎn)化為?+1/-1, 以便 inference 使用

4.2，兩個(gè)問題

• 直接根據(jù)權(quán)重的正負(fù)進(jìn)行二值化：??。符號(hào)函數(shù) sign(x)?定義如下：?

• 進(jìn)行隨機(jī)的二值化，即對(duì)每一個(gè)權(quán)重，以一定概率取??。

二值權(quán)重的梯度為0，無法進(jìn)行參數(shù)更新。為解決這個(gè)問題，需要對(duì)符號(hào)函數(shù)進(jìn)行放松，即用??來代替??。當(dāng) x 在區(qū)間 [-1,1] 時(shí)，存在梯度值 1，否則梯度為 0 。

4.3，二值連接算法改進(jìn)

其中??為該層的輸入張量，??為該層的一個(gè)濾波器，??為該濾波器所對(duì)應(yīng)的二值權(quán)重。

這里，Rastegari 等人認(rèn)為單靠二值運(yùn)算，很難達(dá)到原單精度卷積元素的結(jié)果，于是他們使用了一個(gè)單精度放縮因子??來對(duì)二值濾波器卷積后的結(jié)果進(jìn)行放縮。而??的取值，則可根據(jù)優(yōu)化目標(biāo)：

?得到??。二值連接改進(jìn)的算法訓(xùn)練過程與之前的算法大致相同，不同的地方在于梯度的計(jì)算過程還考慮了??的影響。由于??這個(gè)單精度的縮放因子的存在，有效降低了重構(gòu)誤差，并首次在 ImageNet 數(shù)據(jù)集上取得了與 Alex-Net 相當(dāng)?shù)木取Ｈ缦聢D所示：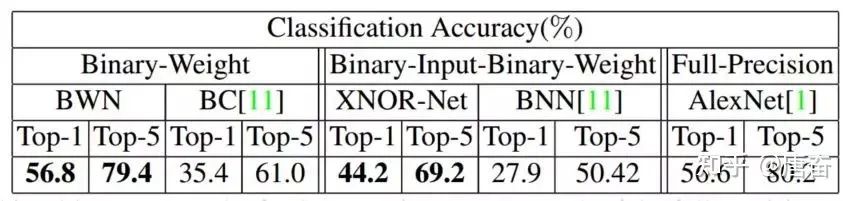

4.4，二值網(wǎng)絡(luò)設(shè)計(jì)注意事項(xiàng)

• 不要使用 kernel = (1, 1) 的 Convolution （包括 resnet 的 bottleneck）：二值網(wǎng)絡(luò)中的 weight 都為 1bit， 如果再是 1x1 大小， 會(huì)極大地降低表達(dá)能力
• 增大 Channel 數(shù)目 + 增大 activation bit 數(shù) 要協(xié)同配合：如果一味增大 channel 數(shù)， 最終 feature map 因?yàn)?bit 數(shù)過低， 還是浪費(fèi)了模型容量。同理反過來也是。
• 建議使用 4bit 及以下的?activation bit， 過高帶來的精度收益變小， 而會(huì)顯著提高 inference 計(jì)算量

05

本文只簡(jiǎn)單介紹這個(gè)領(lǐng)域的開篇之作-Distilling the Knowledge in a Neural Network，這是蒸 "logits"方法，后面還出現(xiàn)了蒸 "features" 的論文。想要更深入理解，中文博客可參考這篇文章-知識(shí)蒸餾是什么？一份入門隨筆(https://zhuanlan.zhihu.com/p/90049906)。

知識(shí)蒸餾（knowledge distillation）(https://arxiv.org/abs/1503.02531)，是遷移學(xué)習(xí)（transfer learning）的一種，簡(jiǎn)單來說就是訓(xùn)練一個(gè)大模型（teacher）和一個(gè)小模型（student），將龐大而復(fù)雜的大模型學(xué)習(xí)到的知識(shí)，通過一定技術(shù)手段遷移到精簡(jiǎn)的小模型上，從而使小模型能夠獲得與大模型相近的性能。

在知識(shí)蒸餾的實(shí)驗(yàn)中，我們先訓(xùn)練好一個(gè)?teacher?網(wǎng)絡(luò)，然后將?teacher?的網(wǎng)絡(luò)的輸出結(jié)果??作為?student?網(wǎng)絡(luò)的目標(biāo)，訓(xùn)練?student?網(wǎng)絡(luò)，使得?student?網(wǎng)絡(luò)的結(jié)果??接近??，因此，student?網(wǎng)絡(luò)的損失函數(shù)為??。這里 CE 是交叉熵（Cross Entropy），??是真實(shí)標(biāo)簽的?onehot?編碼，??是?teacher?網(wǎng)絡(luò)的輸出結(jié)果，??是 student 網(wǎng)絡(luò)的輸出結(jié)果。

但是，直接使用 teacher 網(wǎng)絡(luò)的 softmax 的輸出結(jié)果 q，可能不大合適。因此，一個(gè)網(wǎng)絡(luò)訓(xùn)練好之后，對(duì)于正確的答案會(huì)有一個(gè)很高的置信度。例如，在 MNIST 數(shù)據(jù)中，對(duì)于某個(gè) 2 的輸入，對(duì)于 2 的預(yù)測(cè)概率會(huì)很高，而對(duì)于 2 類似的數(shù)字，例如 3 和 7 的預(yù)測(cè)概率為 10?6 和 10?9。這樣的話，teacher 網(wǎng)絡(luò)學(xué)到數(shù)據(jù)的相似信息（例如數(shù)字 2 和 3，7 很類似）很難傳達(dá)給 student 網(wǎng)絡(luò)，因?yàn)樗鼈兊母怕手到咏?。因此，論文提出了 softmax-T(軟標(biāo)簽計(jì)算公式)公式，如下所示：

這里??是 student 網(wǎng)絡(luò)學(xué)習(xí)的對(duì)象（soft targets），?是 teacher 網(wǎng)絡(luò) softmax 前一層的輸出 logit。如果將??取 1，上述公式變成 softmax，根據(jù) logit 輸出各個(gè)類別的概率。如果??接近于 0，則最大的值會(huì)越近 1，其它值會(huì)接近 0，近似于 onehot 編碼。

所以，可以知道 student 模型最終的損失函數(shù)由兩部分組成：

• 第一項(xiàng)是由小模型(student 模型)的預(yù)測(cè)結(jié)果與大模型的“軟標(biāo)簽”所構(gòu)成的交叉熵（cross entroy）;

• 第二項(xiàng)為小模型預(yù)測(cè)結(jié)果與普通類別標(biāo)簽的交叉熵。

這兩個(gè)損失函數(shù)的重要程度可通過一定的權(quán)重進(jìn)行調(diào)節(jié)，在實(shí)際應(yīng)用中， T 的取值會(huì)影響最終的結(jié)果，一般而言，較大的 T 能夠獲得較高的準(zhǔn)確度，T（蒸餾溫度參數(shù)） 屬于知識(shí)蒸餾模型訓(xùn)練超參數(shù)的一種。T 是一個(gè)可調(diào)節(jié)的超參數(shù)、T 值越大、概率分布越軟（論文中的描述），曲線便越平滑，相當(dāng)于在遷移學(xué)習(xí)的過程中添加了擾動(dòng)，從而使得學(xué)生網(wǎng)絡(luò)在借鑒學(xué)習(xí)的時(shí)候更有效、泛化能力更強(qiáng)，這其實(shí)就是一種抑制過擬合的策略。知識(shí)蒸餾的整個(gè)過程如下圖：

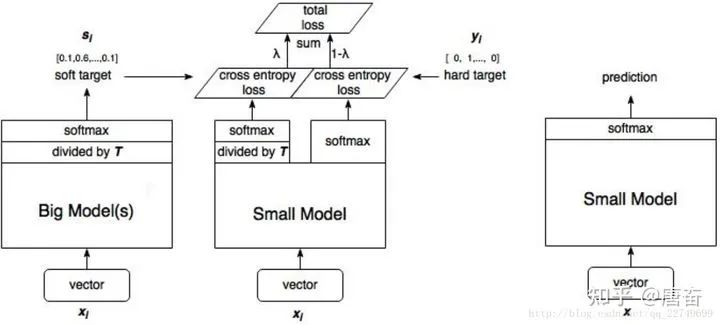
student 模型的實(shí)際模型結(jié)構(gòu)和小模型一樣，但是損失函數(shù)包含了兩部分，分類網(wǎng)絡(luò)的知識(shí)蒸餾 mxnet 代碼示例如下：

# -*-coding-*-  : utf-8  """本程序沒有給出具體的模型結(jié)構(gòu)代碼，主要給出了知識(shí)蒸餾 softmax 損失計(jì)算部分。"""import mxnet as mx
def get_symbol(data, class_labels, resnet_layer_num,Temperature,mimic_weight,num_classes=2):    backbone = StudentBackbone(data)  # Backbone 為分類網(wǎng)絡(luò) backbone 類    flatten = mx.symbol.Flatten(data=conv1, name="flatten")    fc_class_score_s = mx.symbol.FullyConnected(data=flatten, num_hidden=num_classes, name='fc_class_score')    softmax1 = mx.symbol.SoftmaxOutput(data=fc_class_score_s, label=class_labels, name='softmax_hard')
    import symbol_resnet  # Teacher model    fc_class_score_t = symbol_resnet.get_symbol(net_depth=resnet_layer_num, num_class=num_classes, data=data)
    s_input_for_softmax=fc_class_score_s/Temperature    t_input_for_softmax=fc_class_score_t/Temperature
    t_soft_labels=mx.symbol.softmax(t_input_for_softmax, name='teacher_soft_labels')    softmax2 = mx.symbol.SoftmaxOutput(data=s_input_for_softmax, label=t_soft_labels, name='softmax_soft',grad_scale=mimic_weight)    group=mx.symbol.Group([softmax1,softmax2])    group.save('group2-symbol.json')
    return group

tensorflow代碼示例如下：

# 將類別標(biāo)簽進(jìn)行one-hot編碼one_hot = tf.one_hot(y, n_classes,1.0,0.0) # n_classes為類別總數(shù), n為類別標(biāo)簽# one_hot = tf.cast(one_hot_int, tf.float32)teacher_tau = tf.scalar_mul(1.0/args.tau, teacher) # teacher為teacher模型直接輸出張量, tau為溫度系數(shù)Tstudent_tau = tf.scalar_mul(1.0/args.tau, student) # 將模型直接輸出logits張量student處于溫度系數(shù)Tobjective1 = tf.nn.sigmoid_cross_entropy_with_logits(student_tau, one_hot)objective2 = tf.scalar_mul(0.5, tf.square(student_tau-teacher_tau))"""student模型最終的損失函數(shù)由兩部分組成：第一項(xiàng)是由小模型的預(yù)測(cè)結(jié)果與大模型的“軟標(biāo)簽”所構(gòu)成的交叉熵（cross entroy）;第二項(xiàng)為預(yù)測(cè)結(jié)果與普通類別標(biāo)簽的交叉熵。"""tf_loss = (args.lamda*tf.reduce_sum(objective1) + (1-args.lamda)*tf.reduce_sum(objective2))/batch_size

tf.scalar_mul 函數(shù)為對(duì) tf 張量進(jìn)行固定倍率 scalar 縮放函數(shù)。一般 T 的取值在 1 - 20 之間，這里我參考了開源代碼，取值為 3。我發(fā)現(xiàn)在開源代碼中 student 模型的訓(xùn)練，有些是和 teacher 模型一起訓(xùn)練的，有些是 teacher 模型訓(xùn)練好后直接指導(dǎo) student 模型訓(xùn)練。

06

參考資料

1. https://www.cnblogs.com/dyl222/p/11079489.html

2.https://github.com/chengshengchan/model_compression/blob/master/teacher-student.py

3. https://github.com/dkozlov/awesome-knowledge-distillation

4. https://arxiv.org/abs/1603.05279

5. 解析卷積神經(jīng)網(wǎng)絡(luò)-深度學(xué)習(xí)實(shí)踐手冊(cè)

6. https://zhuanlan.zhihu.com/p/81467832