??《數(shù)據(jù)結(jié)構(gòu)與算法系列》帶你了解基本的數(shù)據(jù)結(jié)構(gòu)和常見(jiàn)算法,讓你聽(tīng)到
數(shù)據(jù)結(jié)構(gòu)與算法不再聞風(fēng)喪膽,至少入門(mén)真的不難,凡是困擾你的,給它一個(gè)月攻克它,你會(huì)覺(jué)得你又行了,扶我起來(lái)繼續(xù)學(xué)哈哈。
??關(guān)注我,不迷路,你的支持是我最大的動(dòng)力。
??再小的收獲x365天都會(huì)成就不一樣的自己,一起學(xué)習(xí),一起進(jìn)步。

一、堆(Heap)是一種特殊的樹(shù)
堆是一個(gè)完全二叉樹(shù)(除了最后一層,其他層的節(jié)點(diǎn)個(gè)數(shù)都是滿的,最后一層的節(jié)點(diǎn)都靠左排列);
堆中每一個(gè)節(jié)點(diǎn)的值都必須大于等于(或小于等于)其子樹(shù)中每個(gè)節(jié)點(diǎn)的值。
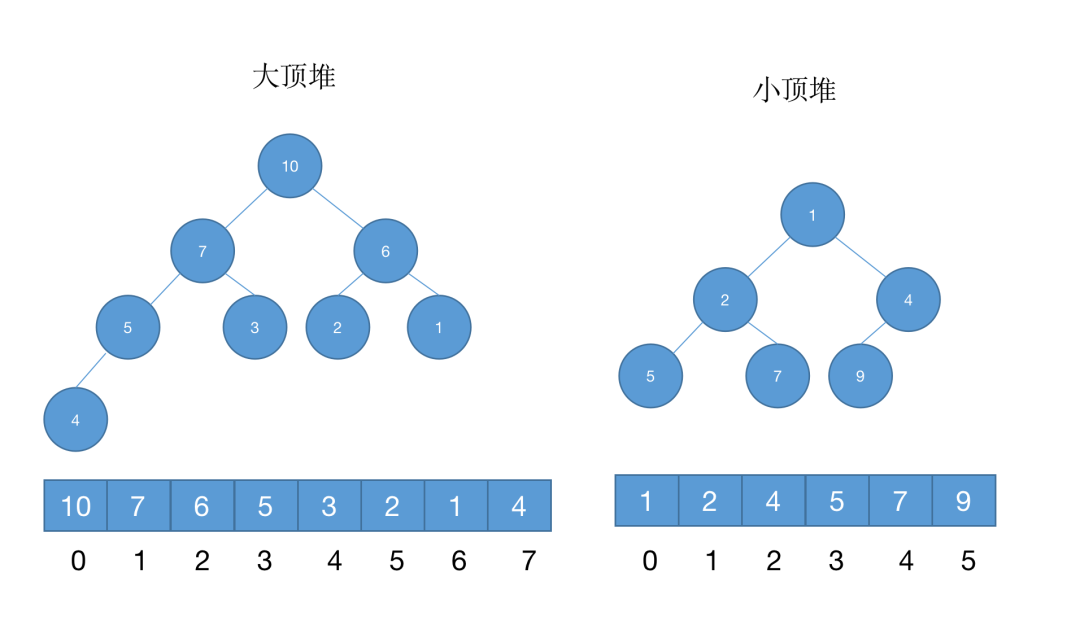
對(duì)于每個(gè)節(jié)點(diǎn)的值都大于等于子樹(shù)中每個(gè)節(jié)點(diǎn)值的堆,我們叫做“大頂堆”。
對(duì)于每個(gè)節(jié)點(diǎn)的值都小于等于子樹(shù)中每個(gè)節(jié)點(diǎn)值的堆,我們叫做“小頂堆”。
二、堆的存儲(chǔ)
完全二叉樹(shù)適合用數(shù)組存儲(chǔ),所以堆也適合用數(shù)組存儲(chǔ)。
因此可得,數(shù)組下標(biāo)是 i 的元素,它的父節(jié)點(diǎn)以及左右子節(jié)點(diǎn)的位置分別是:
parent(i) = floor((i - 1)/2)【向下取整】
left(i) = 2i + 1
right(i) = 2i + 2
三、堆中比較重要的兩個(gè)操作
堆中比較重要的兩個(gè)操作是插入一個(gè)數(shù)據(jù)和刪除堆頂元素。這兩個(gè)操作都要用到堆化(heapify)。
1)插入一個(gè)數(shù)據(jù)的時(shí)候,我們把新插入的數(shù)據(jù)放到數(shù)組的最后,然后從下往上堆化;
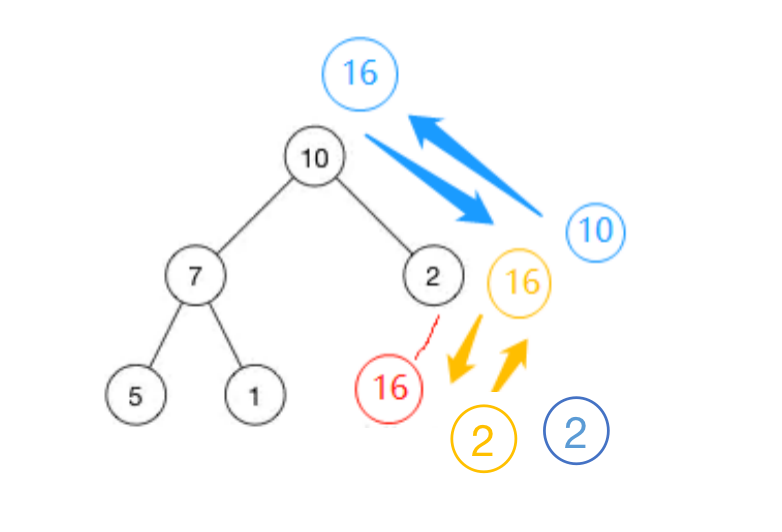
原本存儲(chǔ)[ 10, 7, 2, 5, 1 ],插入16后[ 10, 7, 2, 5, 1,16 ]
在數(shù)組末尾插入新數(shù)據(jù)16后不滿足堆,要進(jìn)行堆化(交換),向上堆化。16與2比較交換,16繼續(xù)向上和10比較交換,最后藍(lán)色狀態(tài)滿足堆,插入結(jié)束。
2)刪除堆頂數(shù)據(jù)的時(shí)候,我們把數(shù)組中的最后一個(gè)元素放到堆頂,然后從上往下堆化。這兩個(gè)操作時(shí)間復(fù)雜度都是 O(logn)。
原本存儲(chǔ)[ 10, 7, 2, 5, 1 ],刪除10后[ 1, 7, 2, 5]
刪除堆頂元素,將數(shù)組末尾的數(shù)交換上來(lái),但是目前不滿足堆的特點(diǎn)了,所以也要進(jìn)行堆化(交換),向下堆化。然后比較1和7(7和2選擇較大的放到堆頂,所以此處選擇1和7交換),繼續(xù)堆化,1和5交換,直到該節(jié)點(diǎn)沒(méi)有任何子節(jié)點(diǎn)或者它比兩個(gè)子節(jié)點(diǎn)都要大,即圖中灰色狀態(tài)滿足堆,結(jié)束。 
小結(jié):完全二叉樹(shù)的高度為log2n ,因此,堆的刪除、插入元素時(shí)間復(fù)雜度為 O(logn)。
四、堆排序
堆排序包括建堆和排序兩個(gè)操作,建堆和排序。
建堆
借助在堆中插入一個(gè)元素的思路。盡管數(shù)組中包含 n 個(gè)數(shù)據(jù),假設(shè)起初堆中只包含一個(gè)數(shù)據(jù),然后依次將n-1個(gè)數(shù)據(jù)依次插入到堆中,這樣,建堆結(jié)束之后,數(shù)組中的數(shù)據(jù)已經(jīng)是按照大頂堆的特性來(lái)組織的。時(shí)間復(fù)雜度是 O(n)。
排序
對(duì)于完全二叉樹(shù)來(lái)說(shuō),下標(biāo)從 n/2 到 n-1 的節(jié)點(diǎn)都是葉子節(jié)點(diǎn),如圖,3214為葉子節(jié)點(diǎn),存儲(chǔ)下標(biāo)從8/2到7。因?yàn)槿~子節(jié)點(diǎn)不需要堆化,每個(gè)節(jié)點(diǎn)堆化的時(shí)間復(fù)雜度是 O(logn),那 n/2個(gè)節(jié)點(diǎn)堆化的總時(shí)間復(fù)雜度就是 O(nlogn) 。
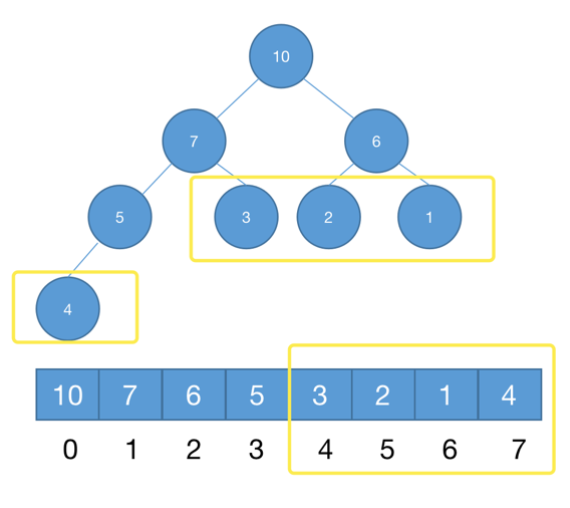
小結(jié):堆排序包括建堆和排序兩個(gè)操作,建堆和排序。建堆過(guò)程的時(shí)間復(fù)雜度是 O(n),排序過(guò)程的時(shí)間復(fù)雜度是 O(nlogn),所以,堆排序整體的時(shí)間復(fù)雜度是 O(nlogn)。
注意:堆排序和快速排序都是 O(nlogn)的算法,甚至堆排序更穩(wěn)定,但是實(shí)際應(yīng)用快速排序會(huì)比較多:原因是對(duì)堆頂節(jié)點(diǎn)進(jìn)行堆化,會(huì)依次訪問(wèn)數(shù)組下標(biāo)是 0,1,3 的元素,而不是像快速排序那樣,局部順序訪問(wèn),所以,這樣對(duì) CPU 緩存是不友好的。另外堆排序比快速排序交換次數(shù)多,可以通過(guò)程序打印比較次數(shù)驗(yàn)證。
五、堆的典型應(yīng)用
1、堆排序
2、優(yōu)先級(jí)隊(duì)列
3、求動(dòng)態(tài)集合中位數(shù)
4、求第K大元素
5、cpu相應(yīng)大于99%的應(yīng)用等等
順便提一下相關(guān)幾個(gè)算法題還是有必要刷的,一般大廠還是容易問(wèn)的。