從一道動態(tài)規(guī)劃題帶你領略『卡特蘭數(shù)』是如何秒殺算法題的
來源公眾號：苦逼的碼農(nóng)
作者：stul
一、 leetcode 96 號題
題目鏈接：https://leetcode-cn.com/problems/unique-binary-search-trees/
題意：給定一個整數(shù) n，求以 1 … n 為節(jié)點組成的二叉搜索樹有多少種？
n = 3 時：
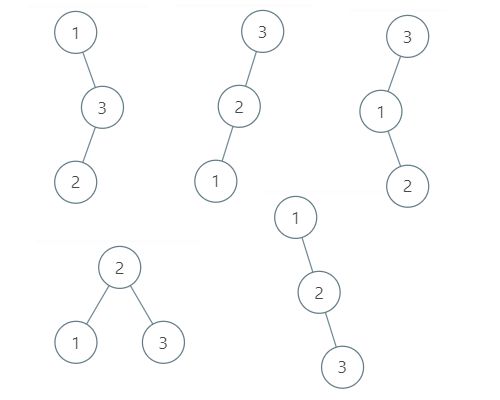
二、動態(tài)規(guī)劃
思路：從 1 開始到 n ，每次以這個數(shù)為根，左子樹存放比它小的數(shù)，右子樹存放比它大的數(shù)。每個根不重復，因此每個樹也必定不重復。
左子樹和右子樹，又可以按照這個規(guī)則去生成新的樹。
例如：n = 3的時候
1為根：比 1 小的數(shù)只有 0，不用管。比 1 大的數(shù)有 2 和 3。
拿 2 和 3 來生成一棵樹和拿 1 和 2 來生成一棵樹的種數(shù)是不是相同的？那么 1 和 2 能生成多少種樹呢？
2為根：比 2 小的是 1，比 2 大的是 3。這里只有 1 種。
3為根：比 3 小的是 1 和 2，1 和 2 能生成多少種樹呢？
我們先暫停思維，來到一個新的問題。n = 2 的時候，結果應該是多少？
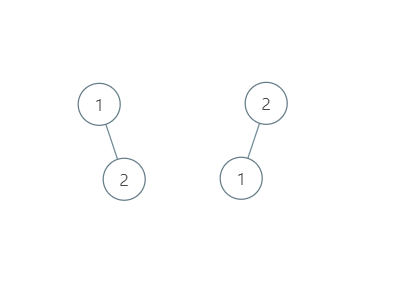
n = 2 的時候，按照我們之前的方法。
1 為根：比 1 大的數(shù)只有 2， 這里有 1 種。
2 為根：比 2 小的數(shù)只有 1， 這里有 1 種。
那答案就應該是 2 種。
解決了 n = 2 的問題，那 n = 3 的問題就也解決了。ans = 2 + 1 + 2 = 5。
我們來看一般情況。輸入一個 n 。
定義一個 F(i) 表示以 i 為根，生成的樹的種數(shù)。
定義一個 G(n) 表示輸入 n 的時候，輸出的結果。此處一定要注意 F 與 G 的區(qū)別。
以 i 為根的時候，能生成多少種樹？
比 i 小的有 i - 1 個，比 i 大的有 n - i 個。因此左子樹有 i - 1 個， 右子樹有 n - i 個數(shù)。那么，F(xiàn)(i) = G(i - 1) * G(n - i)。
而我們求的 G(n) = F(1) + F(2) + …… + F(n)。
把兩個公式綜合 ：
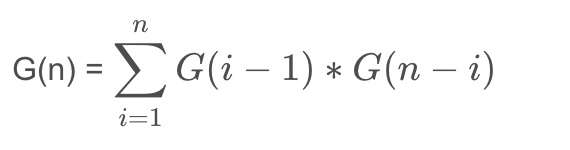
d[0]?=?1;?//?0?的時候特殊處理
for?(int?i?=?1;?i?<=?n;?i++)
????for?(int?j?=?1;?j?<=?i;?j++)?
????????d[i]?+=?d[j-1]?*?d[i-j];?
以上是利用動態(tài)規(guī)劃求解的思路。
時間復雜度：O(n^2)
空間復雜度：O(n)
三、 Catalan公式
這個題目還有一種很強的解法，卡特蘭公式。卡特蘭公式和排列組合有很大關系，不屬于偏難怪解法，有很多算法和數(shù)據(jù)結構的問題本質上就是卡特蘭公式的應用。比如二叉樹的形態(tài)數(shù)，出棧序列數(shù)，括號匹配問題等。公式不要緊，沒必要去硬背。主要是理解卡特蘭問題應用的特征，把問題抽象到已有模型中來。
Catalan 遞推項滿足：
C(n) = C(0) * C(n-1) + C(1) * C(n-2) + … + C(n-2) * C(1) + C(n-1) * C(0)
Catalan 通項公式：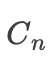
= 
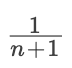
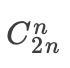
Catalan 遞推公式1：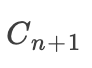
= 
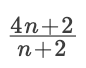
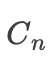
Catalan 性質： = -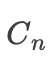
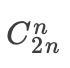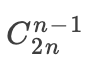
這個題目里面，由我們上面的 G(n) 很容易可以看出是一個卡特蘭的應用。
我們用它的遞推公式來求解。
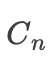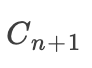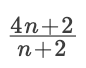
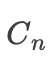求 的值， = 。公式順推，代碼中 n 次循環(huán)結束后的 ans 值就是 
?對應的值。類比斐波那契最簡解法。
????long?ans?=?1;
????for(int?i?=?1;?i?<=?n;?i++)
????????ans?=?ans?*?2?*?(2?*?i?+?1)?/?(i?+?2);
????return?(int)?ans;
時間復雜度：O(n)
空間復雜度：O(1)
四、Catalan應用
例題1：括號序列
給 n 對括號，可以合成的合法序列有多少種？
首先計算一共的序列種數(shù)。n 對括號， 一共有 2n 個位置。我們選出其中 n 個位置放放置左括號，剩下的位置肯定就是右括號了。因此一共的種數(shù)為：
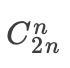。接下來找出非法的括號序列數(shù)。每個非法的序列，在它的奇數(shù)位置，一定存在右括號數(shù)量大于左括號的數(shù)量。
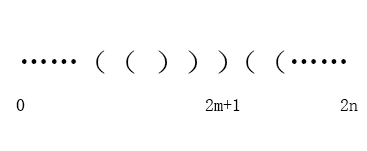
在上圖中：第 2m + 1 的時候，右括號大于左括號，因此該序列非法。
在 2m + 1 前：
右括號數(shù)量為：m + 1
左括號數(shù)量為：m
在 2m + 1后：
總的數(shù)量：n - 2m - 1
左括號有：n - 2m - 1 - (m + 1) = n - m
右括號有：n - 2m - 1 - m = n - m - 1
這個時候我們將右邊的左括號和右括號位置置換(總的組合數(shù)量不會受到影響)。那么在整個序列 2n 個位置中：
右括號的數(shù)量為：m + 1 + n - ?m = n + 1
左括號的數(shù)量為：m + n - m - 1 = n - 1
在長度為 2n 里面有 n + 1 個右括號，數(shù)量為：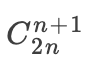
。你也可以理解從左括號的角度去看： 。
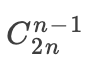在上面兩個步驟以后，我們得到的合法序列數(shù)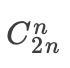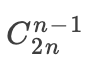： ?- 。這就是 Catalan 公式的性質公式。知道是 Catalan，我們就可以用剛剛的方法求解問題的答案。
例題2 ：一個棧(無窮大)的進棧序列為1，2，3，…，n，有多少個不同的出棧序列?
例題3 ：給出一個n，要求一個長度為2n的01序列，使得序列的任意前綴中1的個數(shù)不少于0的個數(shù)， 有多少個不同的01序列?
例題4 ：2n個人要買票價為五元的電影票，每人只買一張，但是售票員沒有錢找零。其中，n個人持有五元，另外n個人持有十元，問在不發(fā)生找零困難的情況下，有多少種排隊方法？（阿里有個筆試題根據(jù)這個變化的）
其他動態(tài)規(guī)劃算法題推薦：
1、告別動態(tài)規(guī)劃，連刷40道動規(guī)算法題，我總結了動規(guī)的套路
2、動態(tài)規(guī)劃該如何優(yōu)化？我總結了這些套路，以后優(yōu)化就是分分鐘
3、算法專題(動規(guī))：不同的定義產(chǎn)生不同的解法
5、經(jīng)典動態(tài)規(guī)劃：高樓扔雞蛋
推薦閱讀
有必要說一說即將到來的春招（經(jīng)歷+重要性+如何準備）