勾股定理竟然有500種證明方法,你會幾種?


《周髀算經(jīng)》原文記載:

公元前6世紀(jì),古希臘數(shù)學(xué)家畢達(dá)哥拉斯,提出了勾股定理,但證明方法已失傳。所以西方多稱這個定理為畢達(dá)哥拉斯定理。
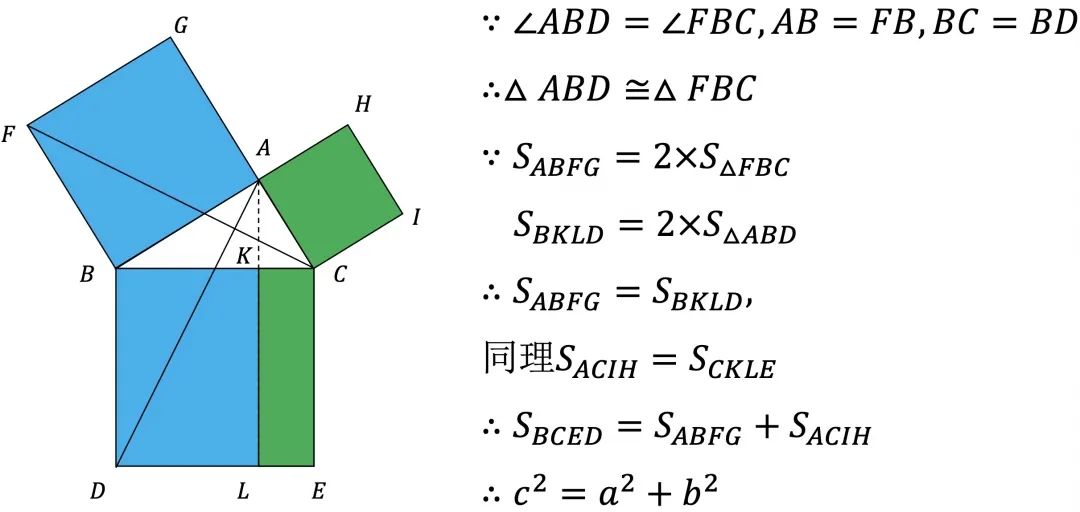
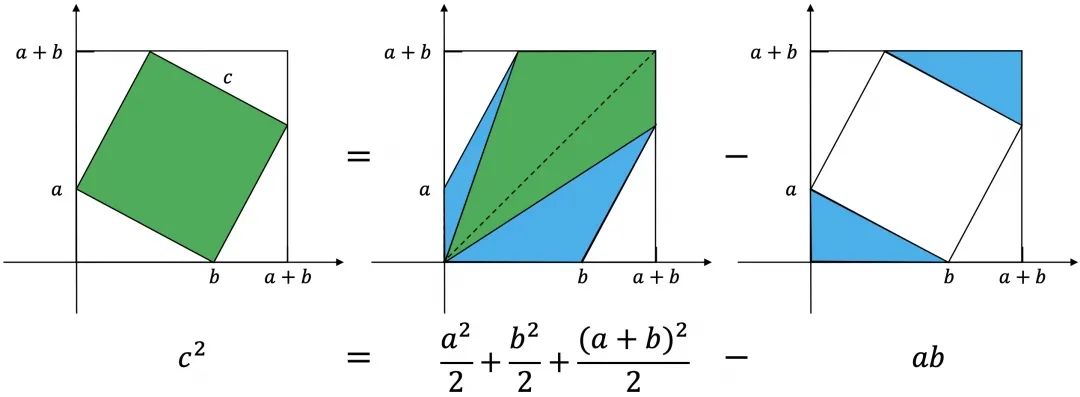
說明:同底等高的長方形面積是三角形面積的2倍,如下同色塊的面積是相等的。
說明:大正方形的面積等于4個直角三角形加上一個小正方形面積之和。

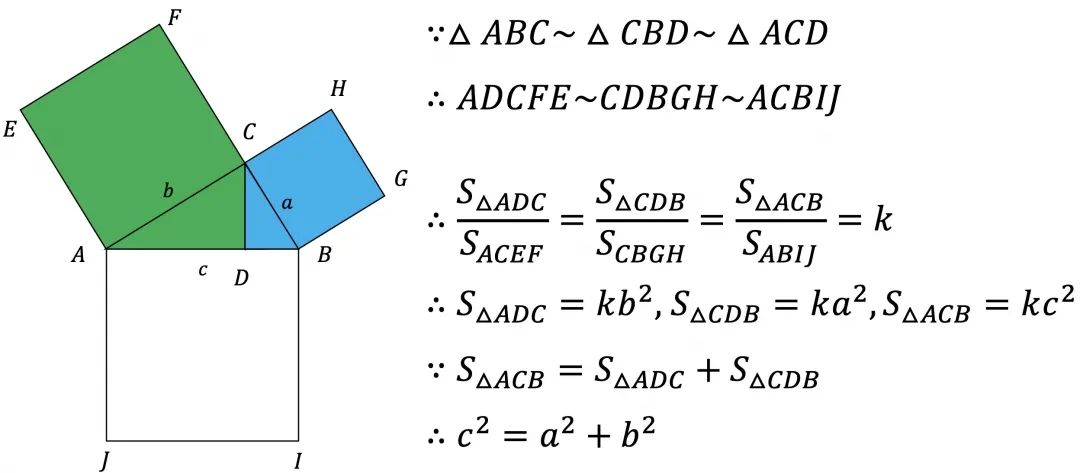
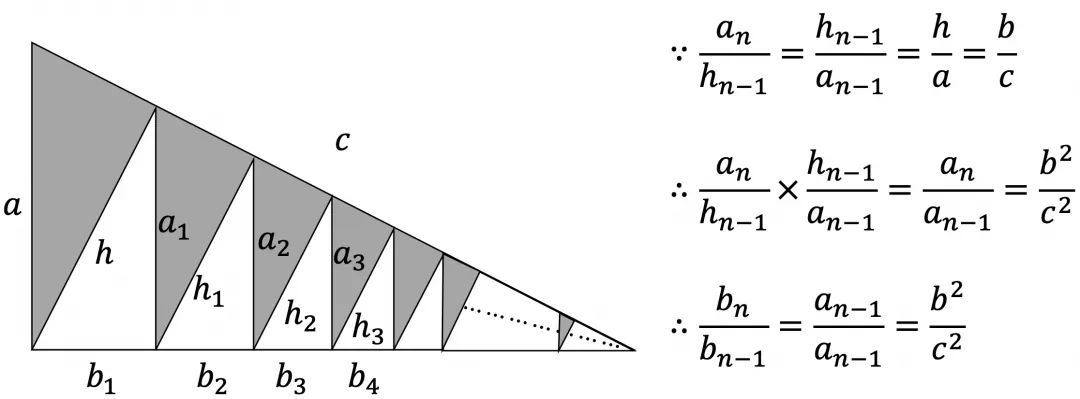
說明:三個直角三角形相似,那么該三角形的面積與以斜邊構(gòu)成的正方形面積之比固定。
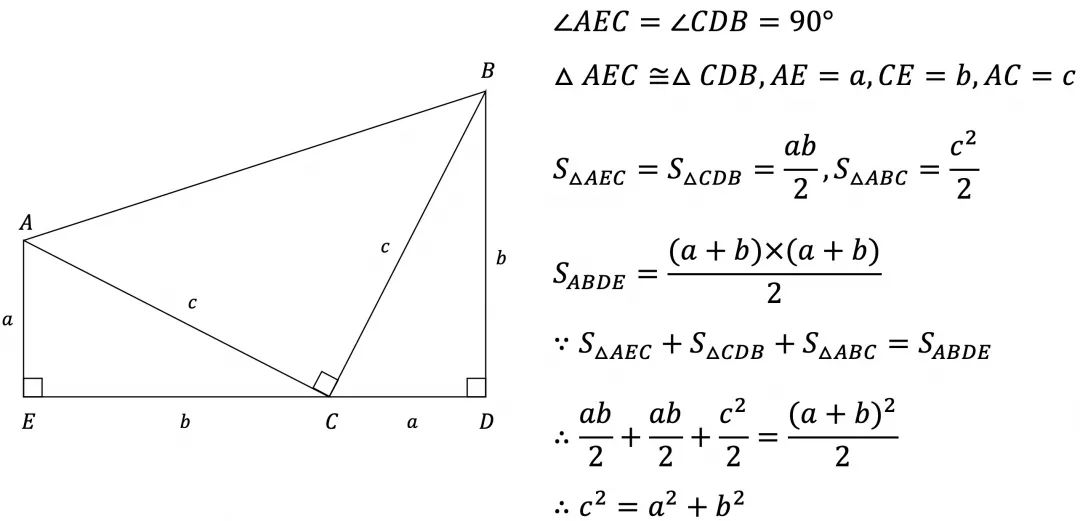
說明:梯形面積等于3個直角三角形的面積之和。
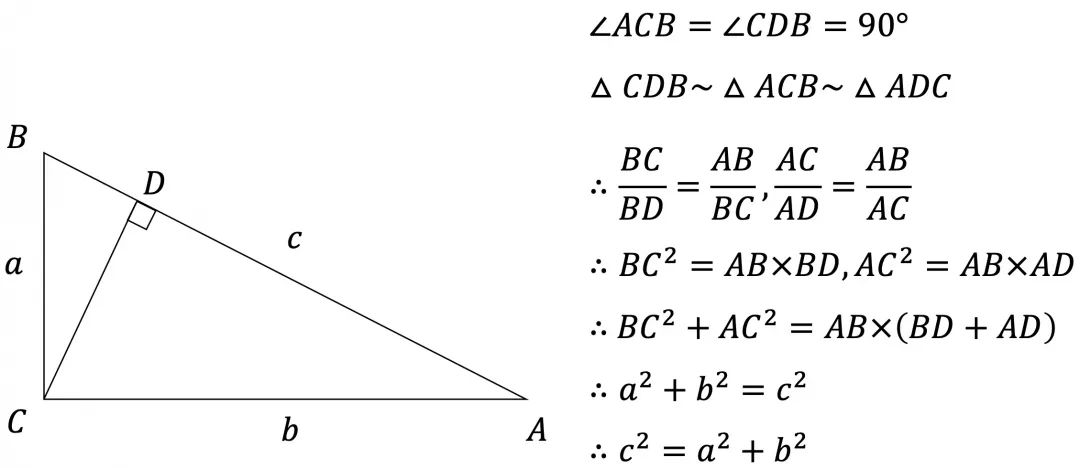





評論
圖片
表情

