PyTorch學(xué)習(xí)系列教程：卷積神經(jīng)網(wǎng)絡(luò)【CNN】

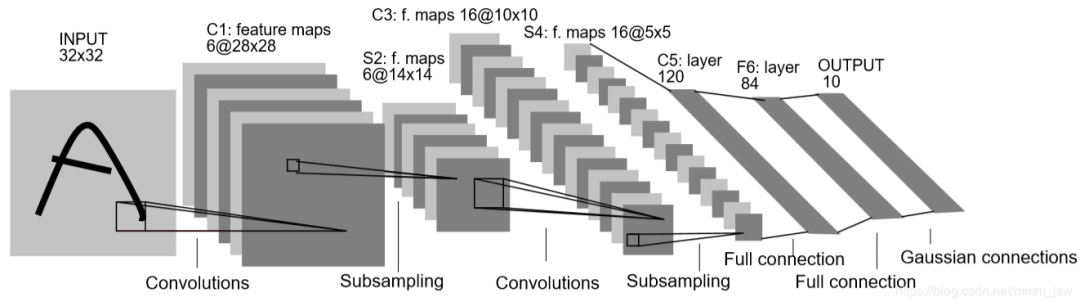
LeNet5——CNN的開山之作

前篇介紹了DNN網(wǎng)絡(luò)，理論上通過增加網(wǎng)絡(luò)層數(shù)可以逼近任意復(fù)雜的函數(shù)，即通用近似定理。但在實(shí)踐過程中，增加網(wǎng)絡(luò)層數(shù)也帶來了兩個(gè)問題：其一是層數(shù)較深的網(wǎng)絡(luò)容易可能存在梯度消失或梯度彌散問題，其二是網(wǎng)絡(luò)層數(shù)的增加也帶來了過多的權(quán)重參數(shù)，對(duì)訓(xùn)練數(shù)據(jù)集和算力資源都帶來了更大的考驗(yàn)。與此同時(shí)，針對(duì)圖像這類特殊的訓(xùn)練數(shù)據(jù)，應(yīng)用DNN時(shí)需要將其具有二維矩陣結(jié)構(gòu)的像素點(diǎn)數(shù)據(jù)拉平成一維向量，而后方可作為DNN的模型輸入——這一過程實(shí)際上丟失了圖片像素點(diǎn)數(shù)據(jù)的方位信息，所以針對(duì)圖像數(shù)據(jù)應(yīng)用DNN也不見得是最優(yōu)解。

在這樣的研究背景下，卷積神經(jīng)網(wǎng)絡(luò)應(yīng)運(yùn)而生，并開啟了深度學(xué)習(xí)的新篇章。延續(xù)前文的行文思路，本篇從以下幾個(gè)方面展開介紹：

• 什么是CNN

• CNN為何有效

• CNN的適用場(chǎng)景

• 在PyTorch中的使用
  

卷積神經(jīng)網(wǎng)絡(luò)，應(yīng)為Convolutional Neural Network，簡(jiǎn)稱CNN，一句話來說就是應(yīng)用了卷積濾波器和池化層兩類模塊的神經(jīng)網(wǎng)絡(luò)。顯然，這里表達(dá)的重點(diǎn)在于CNN網(wǎng)絡(luò)的典型網(wǎng)絡(luò)模塊是卷積濾波器和池化層。所以，這里有必要首先介紹這兩類模塊。

1.卷積濾波器

作為一名通信專業(yè)畢業(yè)人士，我對(duì)卷積一詞并不陌生，最初在信號(hào)處理的課中就有所接觸。當(dāng)然，卷積操作本身應(yīng)該是一個(gè)數(shù)學(xué)層面的操作，對(duì)兩個(gè)函數(shù)f(x)和g(x)做卷積，其實(shí)就是求解以下積分：

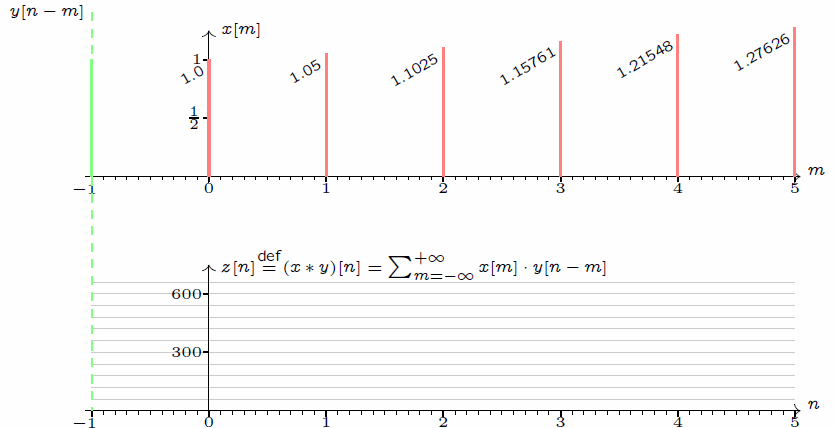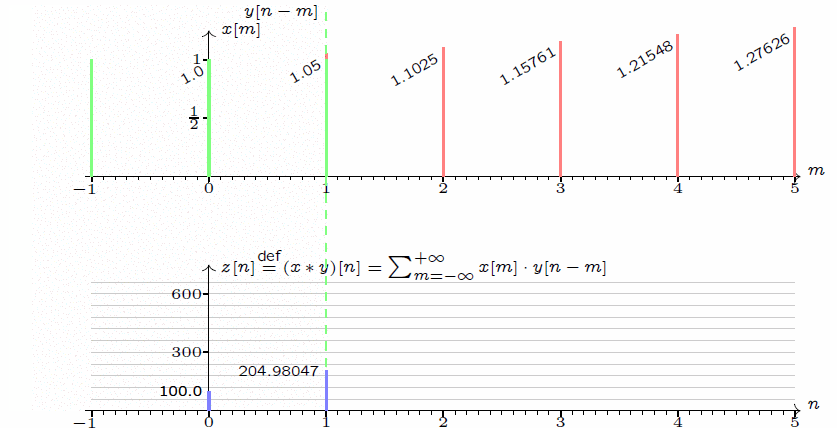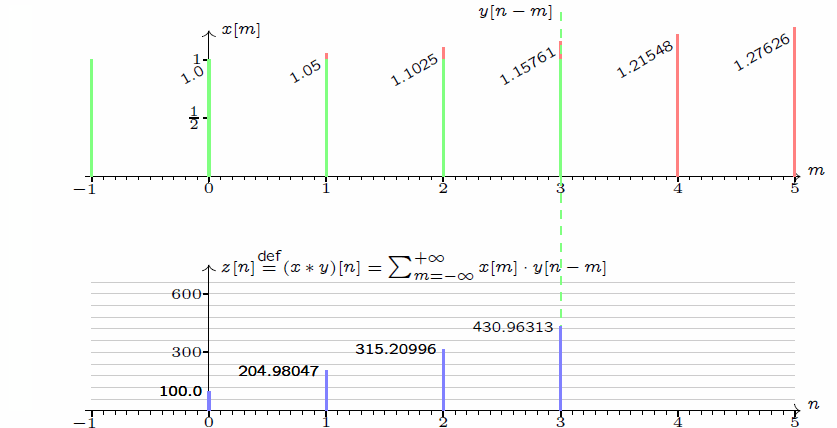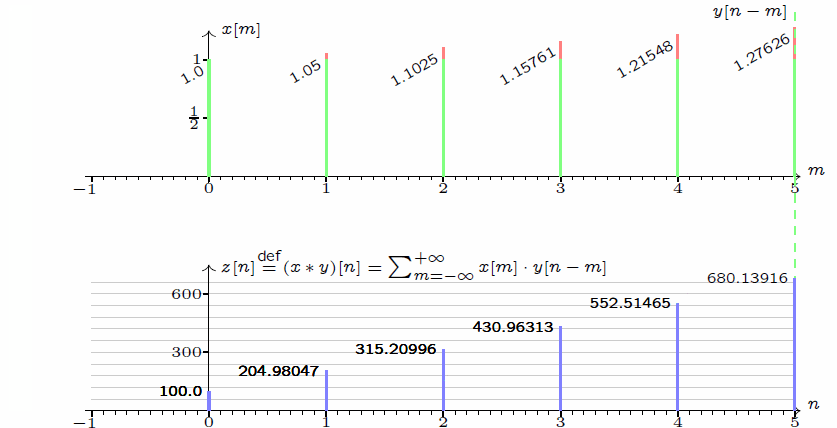
補(bǔ)充說明：在上述卷積操作中，兩個(gè)函數(shù)x()和y()均為單位脈沖函數(shù)，即有值的時(shí)刻均取值為1。而至于說這個(gè)卷積有什么功能和優(yōu)勢(shì)，其實(shí)在通信處理中其最大的價(jià)值在于用于時(shí)域和頻域的變換——時(shí)域卷積等于頻域卷積相乘，用公式表達(dá)就是FFT(f*g) = FFT(f)×FFT(g)，這里FFT表達(dá)信號(hào)處理領(lǐng)域常用的操作：快速傅里葉變換。換句話說，卷積和乘法構(gòu)成了兩個(gè)信號(hào)在時(shí)頻域的交換操作。

ok，了解了卷積操作的功能和其用途之后，我們來看其在神經(jīng)網(wǎng)絡(luò)中能有什么應(yīng)用，或者進(jìn)一步說對(duì)于圖像分類任務(wù)的神經(jīng)網(wǎng)絡(luò)有什么應(yīng)用。

注意到，卷積操作適用于兩個(gè)函數(shù)（連續(xù)積分形式），或者說兩串序列數(shù)據(jù)（離散求和形式）；更進(jìn)一步地，即可通過交錯(cuò)形式逐一得到二者對(duì)位相乘的求和，并得到一個(gè)新的序列結(jié)果。也就是說，兩個(gè)序列卷積的結(jié)果是一個(gè)新的序列。將這對(duì)應(yīng)到用于圖像分類的神經(jīng)網(wǎng)絡(luò)中，有兩個(gè)問題：

• 卷積操作的兩個(gè)對(duì)象（或者說兩串序列）分別是什么呢？一個(gè)應(yīng)該是圖像的像素?cái)?shù)據(jù)，而另一個(gè)則是網(wǎng)絡(luò)權(quán)重，也就是說卷積操作中進(jìn)行滑動(dòng)相乘求和的對(duì)象分別是圖像像素?cái)?shù)據(jù)和網(wǎng)絡(luò)權(quán)重

• 卷積是兩個(gè)一維序列在卷，那應(yīng)用到圖像數(shù)據(jù)呢？難道還是要將其展平為一維序列嗎？——這又回到了DNN中丟失了空間依賴信息的問題。所以，這里卷積操作的范圍又進(jìn)一步由一維序列延伸為二維矩陣——很小的一處改動(dòng)，但卻是CNN的靈魂之處。

除了上述兩個(gè)問題，其實(shí)還隱藏一個(gè)細(xì)節(jié)：卷積之所以用“卷”這個(gè)詞，大概是因?yàn)榫矸e操作的兩個(gè)序列是反向滑動(dòng)的——一個(gè)向左，一個(gè)向右。但無論以什么方向滑動(dòng)，但對(duì)于像素?cái)?shù)據(jù)和網(wǎng)絡(luò)權(quán)重來說，卷積其本質(zhì)是將二者對(duì)位相乘求和。那么，正向?qū)ξ皇菍?duì)位，反向?qū)ξ灰彩菍?duì)位，為何還要卷一下呢——直接正向?qū)ξ徊蛔銐騿幔慨?dāng)然是可以的，所以神經(jīng)網(wǎng)絡(luò)中的卷積都是直接對(duì)位相乘求和。

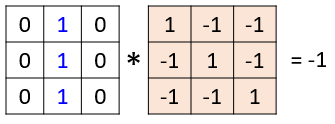
至此，算是真正完成了神經(jīng)網(wǎng)絡(luò)中單個(gè)卷積操作的講解，小結(jié)一下，可概括為以下要點(diǎn)：

• 神經(jīng)網(wǎng)絡(luò)中的卷積操作源起于數(shù)學(xué)中的卷積，但取消了反向滑動(dòng)的特點(diǎn)，而僅采用正向?qū)ξ幌喑说奶匦浴獜倪@個(gè)角度講，神經(jīng)網(wǎng)絡(luò)中的卷積叫做加權(quán)求和更貼切

• 神經(jīng)網(wǎng)絡(luò)中卷積操作的兩個(gè)對(duì)象是像素?cái)?shù)據(jù)和網(wǎng)絡(luò)權(quán)重，其中這里的網(wǎng)絡(luò)權(quán)重也叫做一個(gè)卷積核（kernel），且要求二者尺寸相同

• 神經(jīng)網(wǎng)絡(luò)中的單詞卷積操作只保留一個(gè)輸出
  

類似于DNN網(wǎng)絡(luò)中的神經(jīng)元結(jié)構(gòu)，在CNN網(wǎng)絡(luò)中上述單個(gè)卷積核的操作應(yīng)該叫做一個(gè)神經(jīng)元。那么，有了單個(gè)神經(jīng)元，就可以很容易的通過滑動(dòng)的形式將其推廣到整張圖像：整張的含義既包括橫向和縱向，也包括多個(gè)通道，例如彩色圖片的RGB。所以，在一幅圖像上做卷積操作，就是如下過程：

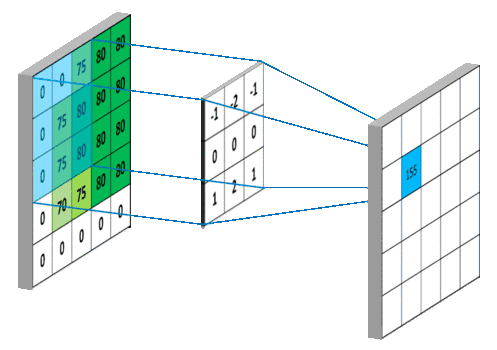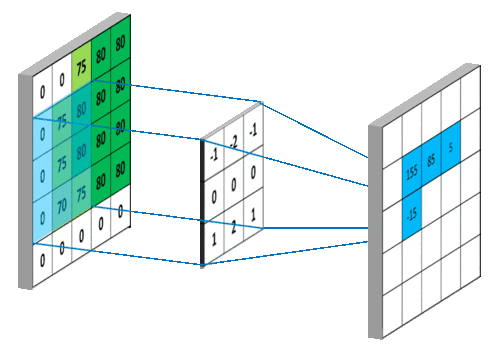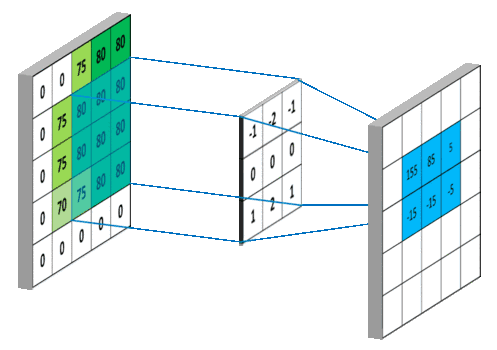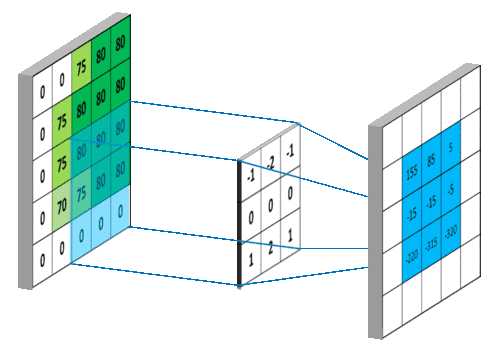
注：一組卷積模板組成的矩陣稱作卷積核，一個(gè)卷積核僅作用于單個(gè)輸入通道上，若前一層有M個(gè)通道，后一層輸出N個(gè)通道，則需要M×N個(gè)卷積核。除原始圖片輸入數(shù)據(jù)外，后續(xù)經(jīng)過卷積層提取的每個(gè)通道都叫做一個(gè)特征圖。

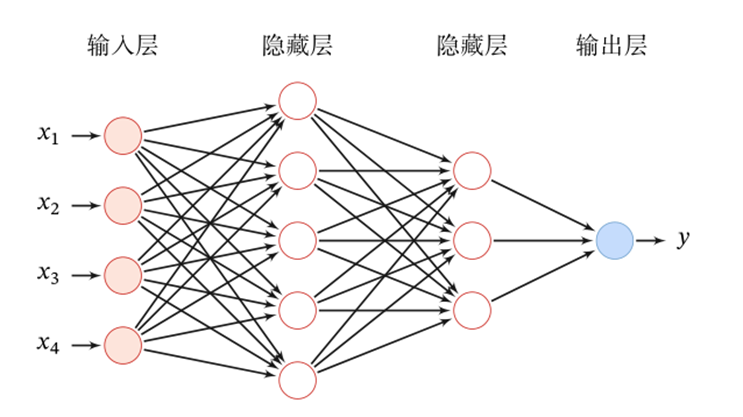
對(duì)比DNN和CNN兩種網(wǎng)絡(luò)，可以窺探更深層的對(duì)比：

• CNN的網(wǎng)絡(luò)結(jié)構(gòu)體現(xiàn)的也是相鄰網(wǎng)絡(luò)層之間的連接關(guān)系，但這種連接僅考慮了小范圍的輸入，即局部連接而非全連接

• 與DNN中各神經(jīng)元擁有不同的連接權(quán)重相比，CNN中的連接權(quán)重只有一套公共的模板，即權(quán)重共享
  

局部連接、權(quán)重共享，這是CNN的兩大特性，也正是這兩大特性，一方面大大降低了權(quán)重參數(shù)的數(shù)量，另一方面也更容易提取圖像數(shù)據(jù)的局部特征！

2.池化層

池化層，英文為pooling，其實(shí)單純從其英文是很難理解為何要在卷積神經(jīng)網(wǎng)絡(luò)中設(shè)計(jì)一個(gè)這樣的結(jié)構(gòu)。雖然目前我個(gè)人未能理解這個(gè)名字的含義，但其功能卻是非常直觀和簡(jiǎn)單的——如果說卷積濾波器是用于局部特征提取的話，那么池化層可以看做是局部特征降維。

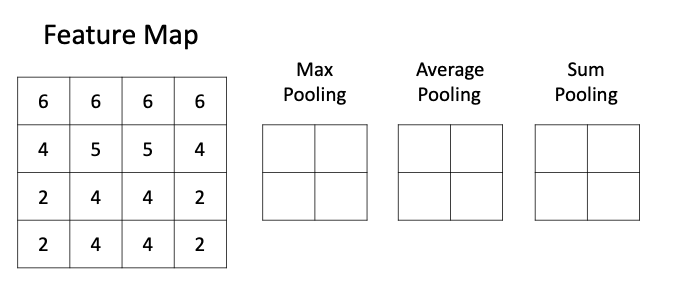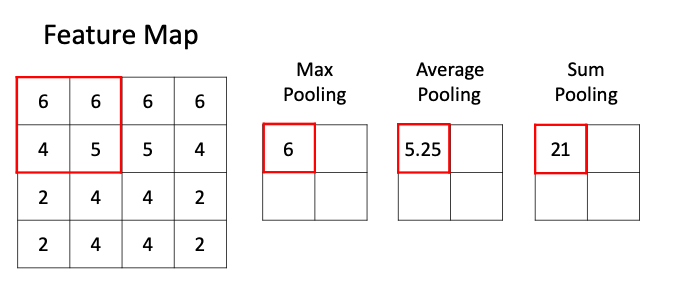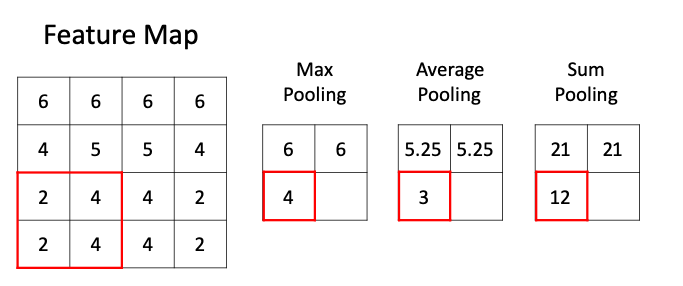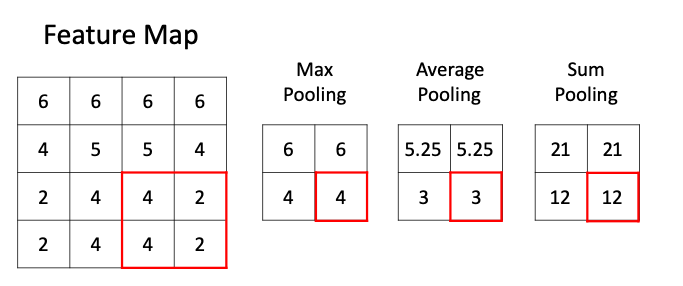
池化層的功能是非常容易理解的，那么設(shè)計(jì)的目的是什么呢?答案有兩個(gè)：

• 數(shù)據(jù)降維，即將大尺寸圖像數(shù)據(jù)變?yōu)樾〕叽?/span>

• 特殊特征提取操作，即池化層其實(shí)也可看做是一種特殊的特征提取器（當(dāng)然，與卷積核的滑動(dòng)特征提取還是有顯著的功能差異的）

至此，有了卷積層和池化層這兩大模塊的理解，即可用其堆疊出想要的卷積神經(jīng)網(wǎng)絡(luò)，例如在開篇給出的CNN開山之作——LeNet5中，則是一個(gè)含有兩個(gè)卷積層、兩個(gè)池化層和三個(gè)全連接層組成的網(wǎng)絡(luò)。

上面從數(shù)學(xué)中的卷積操作開始，介紹了卷積神經(jīng)網(wǎng)絡(luò)中的卷積是如何設(shè)計(jì)的。實(shí)際上，當(dāng)理解了卷積的編碼實(shí)現(xiàn)之后，會(huì)發(fā)現(xiàn)其實(shí)卷積的計(jì)算還是非常簡(jiǎn)單的，一句話概括就是——卷積操作就是用卷積核中的權(quán)重矩陣通過滑窗的形式依次與圖像像素?cái)?shù)據(jù)進(jìn)行相乘求和的過程。

那么問題來了，為什么這樣的設(shè)計(jì)是有效的？換言之，原始的圖像數(shù)據(jù)經(jīng)過卷積操作之后提取到了哪些特征？這就是接下來要介紹的內(nèi)容。

CNN為何有效，回答這一問題的核心在于解釋卷積操作為何有效，因?yàn)镃NN網(wǎng)絡(luò)中的標(biāo)志性操作是卷積。

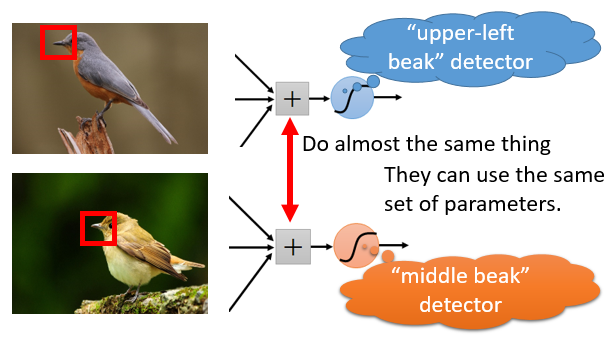
圖片源自臺(tái)大李宏毅教授的深度學(xué)習(xí)PPT

在上述圖片中，我們可以看到同樣是檢測(cè)鳥嘴(beak)的局部特征，通過選用相同的卷積核與其濾波，通過多次變換可以用以分辨其是一個(gè)尖嘴還是短嘴，從而為最終鳥的分類任務(wù)提供一個(gè)特征。

當(dāng)然，這只是一個(gè)示意描述，那么實(shí)際情況如何呢？我們選用LeNet5對(duì)手寫數(shù)字分類任務(wù)加以嘗試，看看模型是怎么利用這一卷積操作。這里沿用深度學(xué)習(xí)模型搭建的三部曲：PyTorch學(xué)習(xí)系列教程：構(gòu)建一個(gè)深度學(xué)習(xí)模型需要哪幾步？

首先是mnist數(shù)據(jù)集的準(zhǔn)備，可直接使用torchvision包在線下載：

from torchvision import datasetsfrom?torch.utils.data?import?DataLoader,?TensorDataset
train = datasets.MNIST('data/', download=True, train=True)test = datasets.MNIST('data/', download=True, train=False)
X_train = train.data.unsqueeze(1)/255.0y_train = train.targetstrainloader = DataLoader(TensorDataset(X_train, y_train), batch_size=256, shuffle=True)
X_test = test.data.unsqueeze(1)/255.0y_test = test.targets

然后是LeNet5的網(wǎng)絡(luò)模型（torchvision中內(nèi)置了部分經(jīng)典模型，但LeNet5由于比較簡(jiǎn)單，不在其中）

import torchfrom?torch import nn
class LeNet5(nn.Module):    def __init__(self):        super().__init__()        self.conv1 = nn.Conv2d(1, 6, 5, padding=2)        self.pool1 = nn.MaxPool2d((2, 2))        self.conv2 = nn.Conv2d(6, 16, 5)        self.pool2 = nn.MaxPool2d((2, 2))        self.fc1 = nn.Linear(16*5*5, 120)        self.fc2 = nn.Linear(120, 84)        self.fc3 = nn.Linear(84, 10)
    def forward(self, x):        x = F.relu(self.conv1(x))        x = self.pool1(x)        x = F.relu(self.conv2(x))        x = self.pool2(x)        x = x.view(len(x), -1)        x = F.relu(self.fc1(x))        x = F.relu(self.fc2(x))        x = self.fc3(x)        return x

最后是模型的訓(xùn)練過程：

model = LeNet5()optimizer = optim.Adam(model.parameters())criterion = nn.CrossEntropyLoss()
for epoch in trange(10):    for X, y in trainloader:        pred = model(X)        loss = criterion(pred, y)        optimizer.zero_grad()        loss.backward()        optimizer.step()    with torch.no_grad():        y_pred = model(X_train)        acc_train = (y_pred.argmax(dim=1) == y_train).float().mean().item()        y_pred = model(X_test)        acc_test = (y_pred.argmax(dim=1) == y_test).float().mean().item()        print(epoch, acc_train, acc_test)### 訓(xùn)練結(jié)果 ### 10%|████████▎                                                                          | 1/10 [00:28<04:12, 28.05s/it]0 0.9379666447639465 0.9406999945640564 20%|████████████████▌                                                                  | 2/10 [00:56<03:48, 28.54s/it]1 0.9663333296775818 0.9685999751091003 30%|████████████████████████▉                                                          | 3/10 [01:25<03:21, 28.76s/it]2 0.975350022315979 0.9771000146865845 40%|█████████████████████████████████▏                                                 | 4/10 [01:54<02:52, 28.78s/it]3 0.9786166548728943 0.9787999987602234 50%|█████████████████████████████████████████▌                                         | 5/10 [02:22<02:22, 28.43s/it]4 0.9850000143051147 0.9853000044822693 60%|█████████████████████████████████████████████████▊                                 | 6/10 [02:51<01:53, 28.49s/it]5 0.9855666756629944 0.9843999743461609 70%|██████████████████████████████████████████████████████████                         | 7/10 [03:20<01:26, 28.78s/it]6 0.9882833361625671 0.9873999953269958 80%|██████████████████████████████████████████████████████████████████▍                | 8/10 [03:51<00:58, 29.37s/it]7 0.9877333045005798 0.9872000217437744 90%|██████████████████████████████████████████████████████████████████████████▋        | 9/10 [04:21<00:29, 29.54s/it]8 0.9905833601951599 0.9896000027656555100%|██████████████████████████████████████████████████████████████████████████████████| 10/10 [04:49<00:00, 28.93s/it]9 0.9918666481971741 0.9886000156402588??

可見，短短通過10個(gè)epoch的訓(xùn)練，模型在訓(xùn)練集和測(cè)試集上均取得了很好的準(zhǔn)確率得分，其中訓(xùn)練集高達(dá)99%以上，測(cè)試集上也接近99%，說明模型不存在過擬合。

那么接下來我們的重點(diǎn)來了：經(jīng)過LeNet5模型中的兩個(gè)卷積層操作之后，原本的手寫數(shù)字圖片變成了什么形態(tài)？換句話說，提取到了哪些特征?

我們這里舉兩個(gè)特殊case研究一下：

case-1：測(cè)試集樣本0，對(duì)應(yīng)手寫數(shù)字7

1-a：原始圖片：

1-b：經(jīng)過第一層卷積，共提取6個(gè)通道的特征圖

1-c：經(jīng)過第二層卷積，提取16個(gè)通道的特征圖

case-2：測(cè)試集樣本1，對(duì)應(yīng)手寫數(shù)字2

2-a：原始圖片

2-b：經(jīng)過第一層卷積，共提取6個(gè)通道的特征圖

2-c：經(jīng)過第二層卷積，提取16個(gè)通道的特征圖

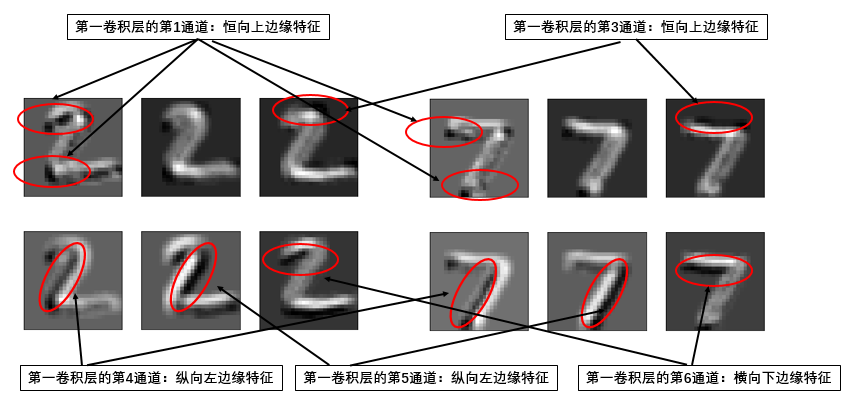
而在此之后的第二卷積層中，則用于提取更為細(xì)節(jié)和豐富的特征，具體可以自行對(duì)比研究一下。至于說為什么提取了這些局部特征就可以完成手寫數(shù)字的識(shí)別——即區(qū)分哪個(gè)是0，哪個(gè)是1等等？這里可以聯(lián)想一下數(shù)字電路中邏輯判斷的例子：對(duì)于由7個(gè)筆畫組成的數(shù)字模板，當(dāng)外圈全亮而中間不亮?xí)r為0，當(dāng)右側(cè)兩個(gè)亮而其他不亮?xí)r為1。而現(xiàn)在LeNet5通過各個(gè)卷積核提取到的特征，就可根據(jù)取值大小對(duì)應(yīng)到圖片中各部分的亮暗情況，進(jìn)而完成數(shù)字的分類。

當(dāng)然，這個(gè)例子只是簡(jiǎn)單的舉例，模型的實(shí)際處理邏輯會(huì)比這復(fù)雜得多——但全靠模型自己去訓(xùn)練和學(xué)習(xí)。

以上，我們首先通過識(shí)別鳥嘴的直觀例子描述了卷積操作在CNN網(wǎng)絡(luò)中扮演的角色——提取局部特征，而后用LeNet5模型在mnist手寫數(shù)字?jǐn)?shù)據(jù)集上的實(shí)際案例加以研究分析，證實(shí)了這一直觀理解。所以，CNN模型之所以有效，其核心在于——卷積操作具有提取圖像數(shù)據(jù)局部特征的能力。

此外，卷積操作配合池化層，其實(shí)還有更魯棒的效果：包括圖像伸縮不變性、旋轉(zhuǎn)不變性等，這是普通的DNN所不具備的能力，此處不再展開。

前面一直在以圖像數(shù)據(jù)為例介紹CNN的原理和應(yīng)用，當(dāng)然圖像數(shù)據(jù)也確實(shí)是CNN網(wǎng)絡(luò)最為擅長(zhǎng)的場(chǎng)景，反之亦然，即最擅長(zhǎng)圖像數(shù)據(jù)的網(wǎng)絡(luò)結(jié)構(gòu)是CNN。

除了圖像數(shù)據(jù)，隨著近年來研究的進(jìn)展，CNN其實(shí)在更多的領(lǐng)域都有所突破和嶄露頭角，例如：

• 將一維卷積應(yīng)用于序列數(shù)據(jù)建模，也可以提取相鄰序列數(shù)據(jù)間的特征關(guān)系，從而很好的完成時(shí)序數(shù)據(jù)建模，例如TCN模型【參考文獻(xiàn)：Temporal convolutional networks: A unified approach to action segmentation.??2016】

• 將二維卷積應(yīng)用于空間數(shù)據(jù)建模，例如交通流量預(yù)測(cè)中，一個(gè)路口的流量往往與其周邊路口的流量大小密切相關(guān)，此時(shí)卷積也是有效的

總而言之，以卷積和池化操作為核心的CNN網(wǎng)絡(luò)，最為適用的場(chǎng)景是圖像數(shù)據(jù)，也可推廣到其他需要提取局部特征的場(chǎng)景。

最后，簡(jiǎn)單介紹一下CNN網(wǎng)絡(luò)中的兩個(gè)關(guān)鍵單元：卷積模塊和池化模塊，在PyTorch中的基本使用。

1.卷積模塊：Conv1d、Conv2d，Conv3d

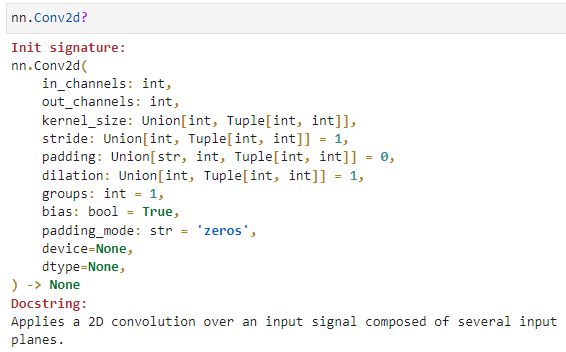
依次說明：

• in_channels：輸入層的圖像數(shù)據(jù)通道數(shù)

• out_channels：輸出層的圖像數(shù)據(jù)通道數(shù)

• kernel_size：卷積核尺寸，既可以是標(biāo)量，代表一個(gè)正方形的卷積核；也可以是一個(gè)二元組，分別代表長(zhǎng)和寬

• stride：卷積核滑動(dòng)的步幅，默認(rèn)情況下為1，即逐像素點(diǎn)移動(dòng)，若設(shè)置大于1的數(shù)值，則可以實(shí)現(xiàn)跨步移動(dòng)的效果
• padding：邊緣填充的層數(shù)，默認(rèn)為0，表示對(duì)原始圖片數(shù)據(jù)不做填充。如果取值大于0，例如padding1，則在原始圖片數(shù)據(jù)的外圈添加一圈0值，注意這里是添加一圈，填充后的圖片尺寸為原尺寸長(zhǎng)和寬均+2。padding=1和stride=2的卷積示意圖如下：

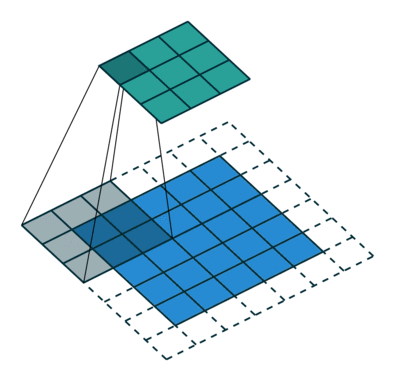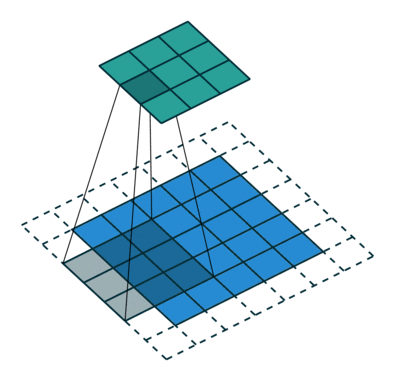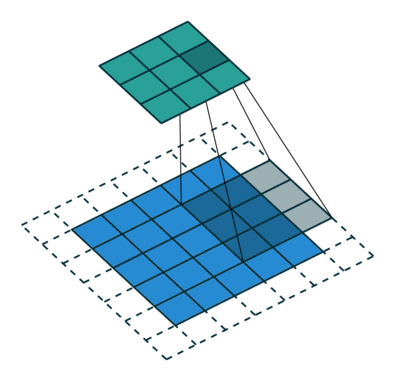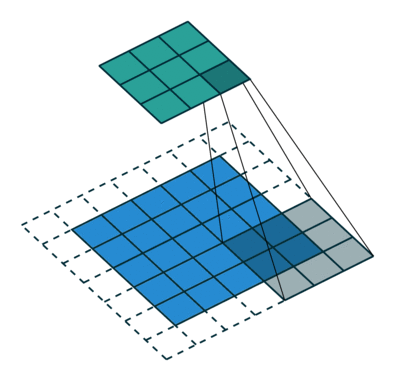
• dilation：用于控制是否是空洞卷積，這是后續(xù)論文新提出的卷積改進(jìn)，即由原始的稠密的卷積核變?yōu)榭斩淳矸e核，用于減小卷積核參數(shù)同時(shí)增大感受野。空洞卷積示意圖如下：

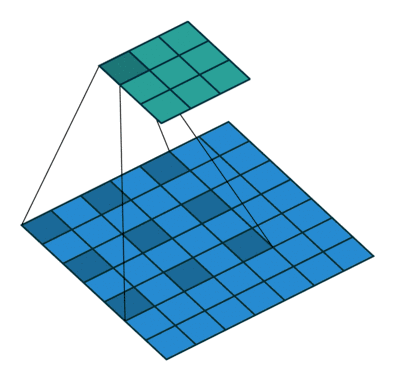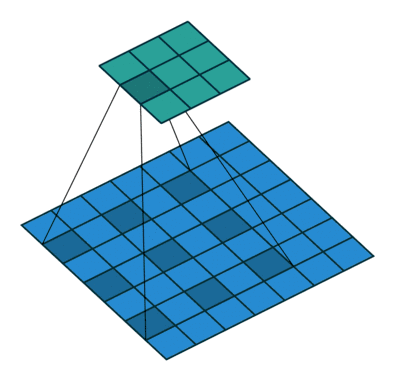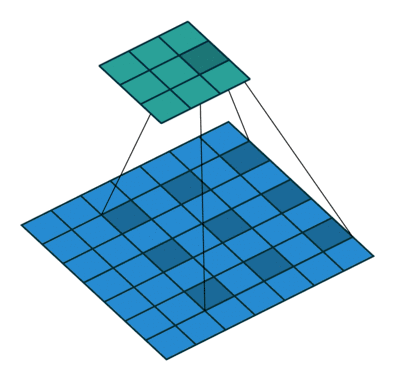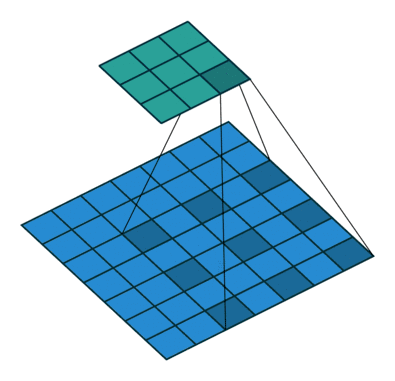
dilation=1的空?卷積

細(xì)品一下stride和dilation兩個(gè)參數(shù)對(duì)卷積操作影響的區(qū)別。

然后是Conv2d的輸入和輸出數(shù)據(jù)。Conv2d可以看做是一個(gè)特殊的神經(jīng)網(wǎng)絡(luò)層，所以其本質(zhì)上是將一個(gè)輸入的tensor變換為另一個(gè)tensor，其中輸入和輸出tensor的尺寸即含義分別如下：

• input：batch × in_channels × height × width

• output:??batch?× output_channels × height?× width

即輸入和輸出tensor主要是圖像通道數(shù)上的改變，圖像的高和寬的大小則要取決于kernel、padding、stride和dilation四個(gè)參數(shù)的綜合作用，這里不再給出具體的計(jì)算公式。?

2.池化模塊：MaxPool1d、MaxPool2d，MaxPool3d

可見，池化模塊的初始化參數(shù)與卷積模塊中的初始化參數(shù)有很多共通之處，包括kernel、stride、padding和dilation等4個(gè)參數(shù)的設(shè)計(jì)上。相應(yīng)的，由于池化層僅僅是各通道上實(shí)現(xiàn)數(shù)據(jù)尺寸的降維，所以其輸入和輸出數(shù)據(jù)的通道數(shù)不變，而僅僅是尺寸的變化，這里也不再給出相應(yīng)的計(jì)算公式。

以上，便是對(duì)卷積神經(jīng)網(wǎng)絡(luò)的一些介紹，從卷積操作的起源、到對(duì)卷積提取局部特征的理解，最后到在PyTorch中的模塊使用，希望對(duì)讀者有所幫助。

相關(guān)閱讀：

• 寫在1024：一名數(shù)據(jù)分析師的修煉之路
  

• 數(shù)據(jù)科學(xué)系列：sklearn庫(kù)主要模塊簡(jiǎn)介
  

• 數(shù)據(jù)科學(xué)系列：seaborn入門詳細(xì)教程
  

• 數(shù)據(jù)科學(xué)系列：pandas入門詳細(xì)教程

• 數(shù)據(jù)科學(xué)系列：matplotlib入門詳細(xì)教程

• 數(shù)據(jù)科學(xué)系列：numpy入門詳細(xì)教程

????????????