一文學(xué)會(huì)遞歸解題

前言

遞歸是算法中一種非常重要的思想，應(yīng)用也很廣，小到階乘,再在工作中用到的比如統(tǒng)計(jì)文件夾大小，大到 Google 的 PageRank 算法都能看到，也是面試官很喜歡的考點(diǎn)

最近看了不少遞歸的文章，收獲不小，不過我發(fā)現(xiàn)大部分網(wǎng)上的講遞歸的文章都不太全面，主要的問題在于解題后大部分都沒有給出相應(yīng)的時(shí)間/空間復(fù)雜度，而時(shí)間/空間復(fù)雜度是算法的重要考量!遞歸算法的時(shí)間復(fù)雜度普遍比較難（需要用到歸納法等），換句話說，如果能解決遞歸的算法復(fù)雜度，其他算法題題的時(shí)間復(fù)雜度也基本不在話下。另外，遞歸算法的時(shí)間復(fù)雜度不少是不能接受的，如果發(fā)現(xiàn)算出的時(shí)間復(fù)雜度過大，則需要轉(zhuǎn)換思路，看下是否有更好的解法 ，這才是根本目的，不要為了遞歸而遞歸！

本文試圖從以下幾個(gè)方面來講解遞歸

1. 什么是遞歸？
2. 遞歸算法通用解決思路
3. 實(shí)戰(zhàn)演練（從初級(jí)到高階）

力爭讓大家對(duì)遞歸的認(rèn)知能上一個(gè)新臺(tái)階，特別會(huì)對(duì)遞歸的精華:時(shí)間復(fù)雜度作詳細(xì)剖析，會(huì)給大家總結(jié)一套很通用的求解遞歸時(shí)間復(fù)雜度的套路，相信你看完肯定會(huì)有收獲

什么是遞歸

簡單地說，就是如果在函數(shù)中存在著調(diào)用函數(shù)本身的情況，這種現(xiàn)象就叫遞歸。

以階乘函數(shù)為例,如下, 在 factorial 函數(shù)中存在著 factorial(n - 1) 的調(diào)用，所以此函數(shù)是遞歸函數(shù)

public int factorial(int n) {
    if (n < =1) {
        return 1;
    }
    return n * factorial(n - 1)
}

進(jìn)一步剖析「遞歸」，先有「遞」再有「歸」，「遞」的意思是將問題拆解成子問題來解決， 子問題再拆解成子子問題，...，直到被拆解的子問題無需再拆分成更細(xì)的子問題（即可以求解），「歸」是說最小的子問題解決了，那么它的上一層子問題也就解決了，上一層的子問題解決了，上上層子問題自然也就解決了,....,直到最開始的問題解決,文字說可能有點(diǎn)抽象，那我們就以階層 f(6) 為例來看下它的「遞」和「歸」。

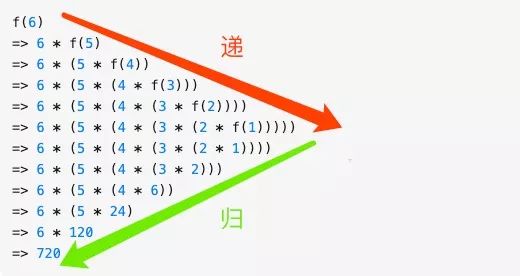
遞歸算法通用解決思路

我們?cè)谏弦还?jié)仔細(xì)剖析了什么是遞歸，可以發(fā)現(xiàn)遞歸有以下兩個(gè)特點(diǎn)

1. 一個(gè)問題可以分解成具有相同解決思路的子問題，子子問題，換句話說這些問題都能調(diào)用同一個(gè)函數(shù)
2. 經(jīng)過層層分解的子問題最后一定是有一個(gè)不能再分解的固定值的（即終止條件）,如果沒有的話,就無窮無盡地分解子問題了，問題顯然是無解的。

所以解遞歸題的關(guān)鍵在于我們首先需要根據(jù)以上遞歸的兩個(gè)特點(diǎn)判斷題目是否可以用遞歸來解。

經(jīng)過判斷可以用遞歸后，接下來我們就來看看用遞歸解題的基本套路（四步曲）：

1. 先定義一個(gè)函數(shù)，明確這個(gè)函數(shù)的功能，由于遞歸的特點(diǎn)是問題和子問題都會(huì)調(diào)用函數(shù)自身，所以這個(gè)函數(shù)的功能一旦確定了， 之后只要找尋問題與子問題的遞歸關(guān)系即可
2. 接下來尋找問題與子問題間的關(guān)系（即遞推公式），這樣由于問題與子問題具有相同解決思路，只要子問題調(diào)用步驟 1 定義好的函數(shù)，問題即可解決。所謂的關(guān)系最好能用一個(gè)公式表示出來，比如 f(n) = n * f(n-) 這樣，如果暫時(shí)無法得出明確的公式，用偽代碼表示也是可以的, 發(fā)現(xiàn)遞推關(guān)系后，要尋找最終不可再分解的子問題的解，即（臨界條件），確保子問題不會(huì)無限分解下去。由于第一步我們已經(jīng)定義了這個(gè)函數(shù)的功能，所以當(dāng)問題拆分成子問題時(shí)，子問題可以調(diào)用步驟 1 定義的函數(shù)，符合遞歸的條件（函數(shù)里調(diào)用自身）
3. 將第二步的遞推公式用代碼表示出來補(bǔ)充到步驟 1 定義的函數(shù)中
4. 最后也是很關(guān)鍵的一步，根據(jù)問題與子問題的關(guān)系，推導(dǎo)出時(shí)間復(fù)雜度,如果發(fā)現(xiàn)遞歸時(shí)間復(fù)雜度不可接受，則需轉(zhuǎn)換思路對(duì)其進(jìn)行改造，看下是否有更靠譜的解法

聽起來是不是很簡單，接下來我們就由淺入深地來看幾道遞歸題，看下怎么用上面的幾個(gè)步驟來套

實(shí)戰(zhàn)演練（從初級(jí)到高階）

熱身賽

輸入一個(gè)正整數(shù)n，輸出n!的值。其中n!=123*…*n,即求階乘

套用上一節(jié)我們說的遞歸四步解題套路來看看怎么解

1. 定義這個(gè)函數(shù)，明確這個(gè)函數(shù)的功能，我們知道這個(gè)函數(shù)的功能是求 n 的階乘, 之后求 n-1, n-2 的階乘就可以調(diào)用此函數(shù)了

/**
 * 求 n 的階乘
 */
public int factorial(int n) {
}

2.尋找問題與子問題的關(guān)系 階乘的關(guān)系比較簡單， 我們以 f(n) 來表示 n 的階乘， 顯然 f(n) = n * f(n - 1), ?同時(shí)臨界條件是 f(1) = 1,即

3.將第二步的遞推公式用代碼表示出來補(bǔ)充到步驟 1 定義的函數(shù)中

/**
 * 求 n 的階乘
 */
public int factorial(int n) {
    // 第二步的臨界條件
    if (n < =1) {
        return 1;
    }

    // 第二步的遞推公式
    return n * factorial(n-1)
}

4.求時(shí)間復(fù)雜度 由于 ?f(n) = n * f(n-1) = n * (n-1) * .... * f(1),總共作了 n 次乘法，所以時(shí)間復(fù)雜度為 n。

看起來是不是有這么點(diǎn)眉目， 當(dāng)然這道題確實(shí)太過簡單,很容易套路，那我們?cè)賮砜催M(jìn)階一點(diǎn)的題

入門題

一只青蛙可以一次跳 1 級(jí)臺(tái)階或一次跳 2 級(jí)臺(tái)階,例如:跳上第 1 級(jí)臺(tái)階只有一種跳法：直接跳 1 級(jí)即可。跳上第 2 級(jí)臺(tái)階有兩種跳法：每次跳 1 級(jí)，跳兩次；或者一次跳 2 級(jí)。問要跳上第 n 級(jí)臺(tái)階有多少種跳法？

我們繼續(xù)來按四步曲來看怎么套路

1.定義一個(gè)函數(shù)，這個(gè)函數(shù)代表了跳上 n 級(jí)臺(tái)階的跳法

/**
 * 跳 n 極臺(tái)階的跳法
 */
public int f(int n) {
}

2.尋找問題與子問題之前的關(guān)系 這兩者之前的關(guān)系初看確實(shí)看不出什么頭緒，但仔細(xì)看題目，一只青蛙只能跳一步或兩步臺(tái)階，自上而下地思考，也就是說如果要跳到 n 級(jí)臺(tái)階只能從 從 n-1 或 n-2 級(jí)跳， 所以問題就轉(zhuǎn)化為跳上 n-1 和 n-2 級(jí)臺(tái)階的跳法了，如果 f(n) 代表跳到 n 級(jí)臺(tái)階的跳法，那么從以上分析可得 f(n) = f(n-1) + f(n-2),顯然這就是我們要找的問題與子問題的關(guān)系,而顯然當(dāng) n = 1, n = 2， 即跳一二級(jí)臺(tái)階是問題的最終解，于是遞推公式系為

3.將第二步的遞推公式用代碼表示出來補(bǔ)充到步驟 1 定義的函數(shù)中 補(bǔ)充后的函數(shù)如下

/**
 * 跳 n 極臺(tái)階的跳法
 */
public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    return f(n-1) + f(n-2)
}

4.計(jì)算時(shí)間復(fù)雜度 由以上的分析可知 f(n) 滿足以下公式

斐波那契的時(shí)間復(fù)雜度計(jì)算涉及到高等代數(shù)的知識(shí)， 這里不做詳細(xì)推導(dǎo)，有興趣的同學(xué)可以點(diǎn)擊這里查看,我們直接結(jié)出結(jié)論

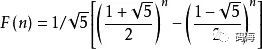
由些可知時(shí)間復(fù)雜度是指數(shù)級(jí)別，顯然不可接受，那回過頭來看為啥時(shí)間復(fù)雜度這么高呢,假設(shè)我們要計(jì)算 f(6),根據(jù)以上推導(dǎo)的遞歸公式，展示如下

可以看到有大量的重復(fù)計(jì)算, f(3) 計(jì)算了 3 次， 隨著 n 的增大，f(n) 的時(shí)間復(fù)雜度自然呈指數(shù)上升了

5.優(yōu)化?

既然有這么多的重復(fù)計(jì)算，我們可以想到把這些中間計(jì)算過的結(jié)果保存起來，如果之后的計(jì)算中碰到同樣需要計(jì)算的中間態(tài)，直接在這個(gè)保存的結(jié)果里查詢即可，這就是典型的 以空間換時(shí)間,改造后的代碼如下

public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;
    // map 即保存中間態(tài)的鍵值對(duì)， key 為 n，value 即 f(n)
    if (map.get(n)) {
        return map.get(n)
    }
    return f(n-1) + f(n-2)
}

那么改造后的時(shí)間復(fù)雜度是多少呢，由于對(duì)每一個(gè)計(jì)算過的 f(n) 我們都保存了中間態(tài) ，不存在重復(fù)計(jì)算的問題，所以時(shí)間復(fù)雜度是 O(n), 但由于我們用了一個(gè)鍵值對(duì)來保存中間的計(jì)算結(jié)果，所以空間復(fù)雜度是 O(n)。問題到這里其實(shí)已經(jīng)算解決了，但身為有追求的程序員，我們還是要問一句,空間復(fù)雜度能否繼續(xù)優(yōu)化?

6.使用循環(huán)迭代來改造算法 我們?cè)诜治鰡栴}與子問題關(guān)系（f(n) = f(n-1) + f(n-2)）的時(shí)候用的是自頂向下的分析方式,但其實(shí)我們?cè)诮?f(n) 的時(shí)候可以用自下而上的方式來解決，通過觀察我們可以發(fā)現(xiàn)以下規(guī)律

f(1) = 1
f(2) = 2
f(3) = f(1) + f(2) = 3
f(4) = f(3) + f(2) = 5
....
f(n) = f(n-1) + f(n-2)

最底層 f(1), f(2) 的值是確定的，之后的 f(3), f(4) ,...等問題都可以根據(jù)前兩項(xiàng)求解出來，一直到 f(n)。所以我們的代碼可以改造成以下方式

public int f(int n) {
    if (n == 1) return 1;
    if (n == 2) return 2;

    int result = 0;
    int pre = 1;
    int next = 2;
    
    for (int i = 3; i < n + 1; i ++) {
        result = pre + next;
        pre = next;
        next = result;
    }
    return result;
}

改造后的時(shí)間復(fù)雜度是 O(n), 而由于我們?cè)谟?jì)算過程中只定義了兩個(gè)變量（pre，next），所以空間復(fù)雜度是O(1)

簡單總結(jié)一下：分析問題我們需要采用自上而下的思維，而解決問題有時(shí)候采用自下而上的方式能讓算法性能得到極大提升,思路比結(jié)論重要

初級(jí)題

接下來我們來看下一道經(jīng)典的題目: 反轉(zhuǎn)二叉樹 將左邊的二叉樹反轉(zhuǎn)成右邊的二叉樹

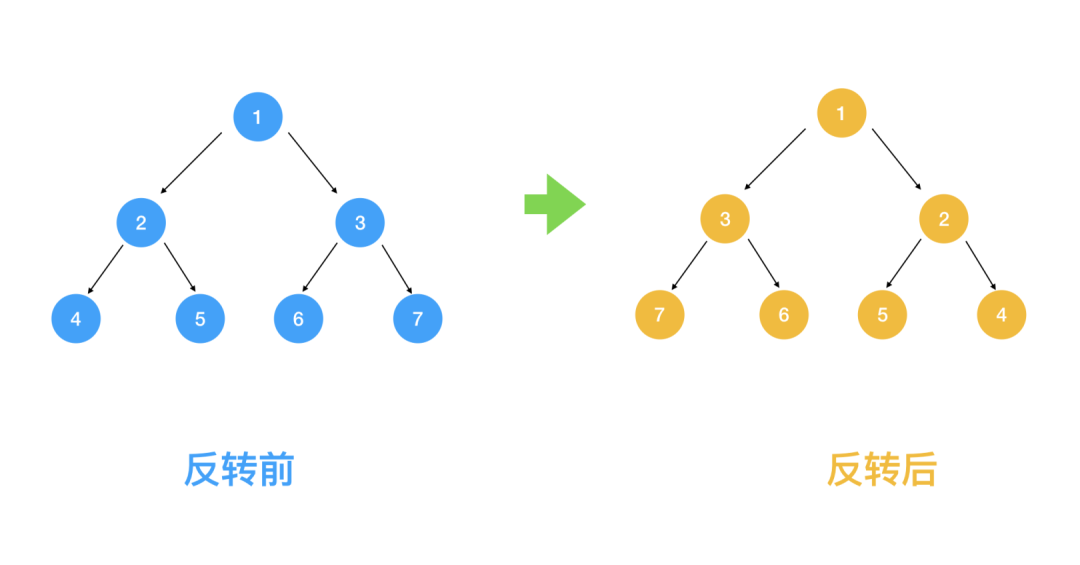
接下來讓我們看看用我們之前總結(jié)的遞歸解法四步曲如何解題?

1.定義一個(gè)函數(shù)，這個(gè)函數(shù)代表了翻轉(zhuǎn)以 root 為根節(jié)點(diǎn)的二叉樹

public static class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public TreeNode invertTree(TreeNode root) {
}

2.查找問題與子問題的關(guān)系,得出遞推公式 我們之前說了，解題要采用自上而下的思考方式，那我們?nèi)∏懊娴?， 2，3 結(jié)點(diǎn)來看，對(duì)于根節(jié)點(diǎn) 1 來說，假設(shè) 2, 3 結(jié)點(diǎn)下的節(jié)點(diǎn)都已經(jīng)翻轉(zhuǎn)，那么只要翻轉(zhuǎn) 2， 3 節(jié)點(diǎn)即滿足需求

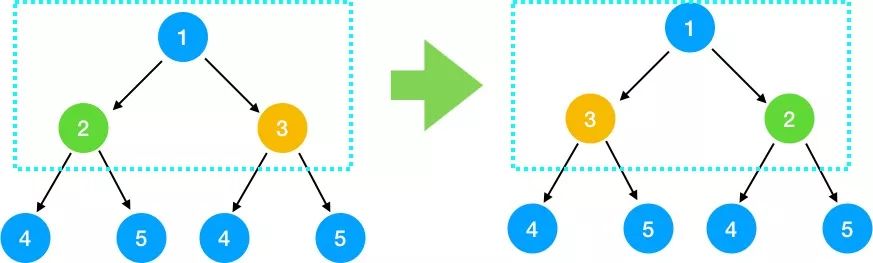
對(duì)于2， 3 結(jié)點(diǎn)來說，也是翻轉(zhuǎn)其左右節(jié)點(diǎn)即可,依此類推,對(duì)每一個(gè)根節(jié)點(diǎn)，依次翻轉(zhuǎn)其左右節(jié)點(diǎn)，所以我們可知問題與子問題的關(guān)系是 翻轉(zhuǎn)(根節(jié)點(diǎn)) = ?翻轉(zhuǎn)(根節(jié)點(diǎn)的左節(jié)點(diǎn)) + 翻轉(zhuǎn)(根節(jié)點(diǎn)的右節(jié)點(diǎn)) 即?

invert(root) = invert(root->left) + invert(root->right)

而顯然遞歸的終止條件是當(dāng)結(jié)點(diǎn)為葉子結(jié)點(diǎn)時(shí)終止（因?yàn)槿~子節(jié)點(diǎn)沒有左右結(jié)點(diǎn)）

3.將第二步的遞推公式用代碼表示出來補(bǔ)充到步驟 1 定義的函數(shù)中

 public TreeNode invertTree(TreeNode root) {
    // 葉子結(jié)果不能翻轉(zhuǎn)
    if (root == null) {
        return null;
    }
    // 翻轉(zhuǎn)左節(jié)點(diǎn)下的左右節(jié)點(diǎn)
    TreeNode left = invertTree(root.left);
    // 翻轉(zhuǎn)右節(jié)點(diǎn)下的左右節(jié)點(diǎn)
    TreeNode right = invertTree(root.right);

    // 左右節(jié)點(diǎn)下的二叉樹翻轉(zhuǎn)好后，翻轉(zhuǎn)根節(jié)點(diǎn)的左右節(jié)點(diǎn)
    root.right = left;
    root.left = right;
    return root;
}

4.時(shí)間復(fù)雜度分析 由于我們會(huì)對(duì)每一個(gè)節(jié)點(diǎn)都去做翻轉(zhuǎn)，所以時(shí)間復(fù)雜度是 O(n)，那么空間復(fù)雜度呢，這道題的空間復(fù)雜度非常有意思，我們一起來看下，由于每次調(diào)用 invertTree 函數(shù)都相當(dāng)于一次壓棧操作， 那最多壓了幾次棧呢， 仔細(xì)看上面函數(shù)的下一段代碼

    TreeNode left = invertTree(root.left);

從根節(jié)點(diǎn)出發(fā)不斷對(duì)左結(jié)果調(diào)用翻轉(zhuǎn)函數(shù), 直到葉子節(jié)點(diǎn)，每調(diào)用一次都會(huì)壓棧，左節(jié)點(diǎn)調(diào)用完后，出棧，再對(duì)右節(jié)點(diǎn)壓棧....,下圖可知棧的大小為3， 即樹的高度，如果是完全二叉樹 ，則樹的高度為logn, 即空間復(fù)雜度為O(logn)

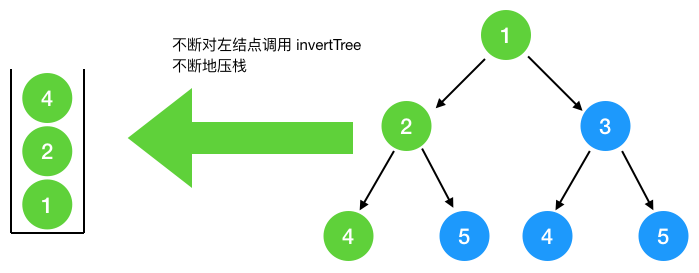
最壞情況，如果此二叉樹是如圖所示(只有左節(jié)點(diǎn)，沒有右節(jié)點(diǎn))，則樹的高度即結(jié)點(diǎn)的個(gè)數(shù) n，此時(shí)空間復(fù)雜度為 O(n),總的來看，空間復(fù)雜度為O(n)

中級(jí)題

接下來我們看一下大學(xué)時(shí)學(xué)過的漢諾塔問題：　　如下圖所示，從左到右有A、B、C三根柱子，其中A柱子上面有從小疊到大的n個(gè)圓盤，現(xiàn)要求將A柱子上的圓盤移到C柱子上去，期間只有一個(gè)原則：一次只能移到一個(gè)盤子且大盤子不能在小盤子上面，求移動(dòng)的步驟和移動(dòng)的次數(shù)

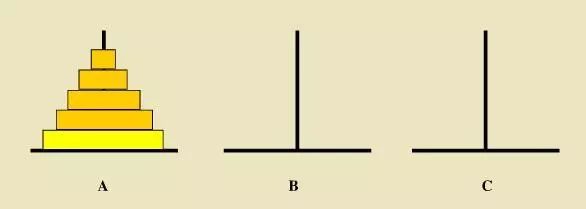
接下來套用我們的遞歸四步法看下這題怎么解

1.定義問題的遞歸函數(shù)，明確函數(shù)的功能,我們定義這個(gè)函數(shù)的功能為：把 A 上面的 n 個(gè)圓盤經(jīng)由 B 移到 C

// 將 n 個(gè)圓盤從 a 經(jīng)由 b 移動(dòng)到 c 上
public void hanoid(int n, char a, char b, char c) {
}

2.查找問題與子問題的關(guān)系 首先我們看如果 A 柱子上只有兩塊圓盤該怎么移

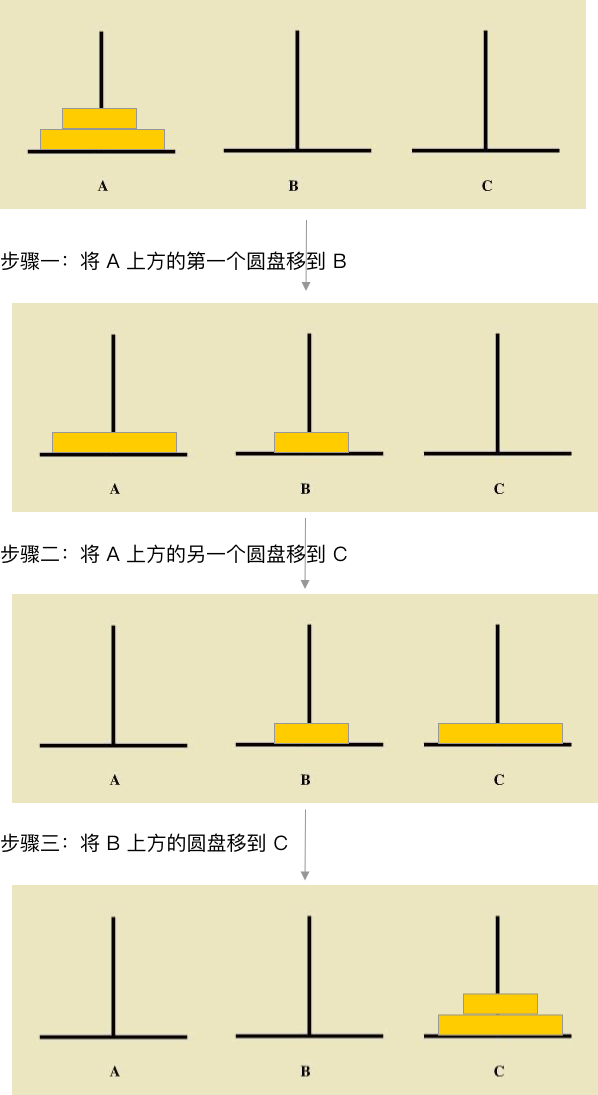
前面我們多次提到，分析問題與子問題的關(guān)系要采用自上而下的分析方式，要將 n 個(gè)圓盤經(jīng)由 B 移到 C 柱上去，可以按以下三步來分析 * 將 上面的 n-1 個(gè)圓盤看成是一個(gè)圓盤,這樣分析思路就與上面提到的只有兩塊圓盤的思路一致了 * 將上面的 ?n-1 個(gè)圓盤經(jīng)由 C 移到 B * 此時(shí)將 A 底下的那塊最大的圓盤移到 C * 再將 B 上的 n-1 個(gè)圓盤經(jīng)由A移到 C上

有人問第一步的 n - 1 怎么從 C 移到 B,重復(fù)上面的過程,只要把 上面的 n-2個(gè)盤子經(jīng)由 A 移到 B, 再把A最下面的盤子移到 C,最后再把上面的 n - 2 的盤子經(jīng)由A 移到 B 下..., 怎么樣，是不是找到規(guī)律了，不過在找問題的過程中 切忌把子問題層層展開,到漢諾塔這個(gè)問題上切忌再分析 n-3,n-4 怎么移，這樣會(huì)把你繞暈，只要找到一層問題與子問題的關(guān)系得出可以用遞歸表示即可。

由以上分析可得

move(n from A to C) = move(n-1 from A to B) + move(A to C) + move(n-1 from B to C`)

一定要先得出遞歸公式，哪怕是偽代碼也好!這樣第三步推導(dǎo)函數(shù)編寫就容易很多，終止條件我們很容易看出，當(dāng) A 上面的圓盤沒有了就不移了

3.根據(jù)以上的遞歸偽代碼補(bǔ)充函數(shù)的功能

// 將 n 個(gè)圓盤從 a 經(jīng)由 b 移動(dòng)到 c 上
public void hanoid(int n, char a, char b, char c) {
    if (n <= 0) {
        return;
    }
    // 將上面的  n-1 個(gè)圓盤經(jīng)由 C 移到 B
    hanoid(n-1, a, c, b);
    // 此時(shí)將 A 底下的那塊最大的圓盤移到 C
    move(a, c);
    // 再將 B 上的 n-1 個(gè)圓盤經(jīng)由A移到 C上
    hanoid(n-1, b, a, c);
}

public void move(char a, char b) {
    printf("%c->%c\n", a, b);
}

從函數(shù)的功能上看其實(shí)比較容易理解，整個(gè)函數(shù)定義的功能就是把 A 上的 n 個(gè)圓盤 經(jīng)由 B 移到 C，由于定義好了這個(gè)函數(shù)的功能，那么接下來的把 n-1 個(gè)圓盤 經(jīng)由 C 移到 B 就可以很自然的調(diào)用這個(gè)函數(shù),所以明確函數(shù)的功能非常重要,按著函數(shù)的功能來解釋，遞歸問題其實(shí)很好解析，切忌在每一個(gè)子問題上層層展開死摳,這樣這就陷入了遞歸的陷阱，計(jì)算機(jī)都會(huì)棧溢出，何況人腦

4.時(shí)間復(fù)雜度分析 從第三步補(bǔ)充好的函數(shù)中我們可以推斷出

f(n) = f(n-1) + 1 + f(n-1) = 2f(n-1) + 1 = 2(2f(n-2) + 1) + 1 = 2 * 2 * f(n-2) + 2 + 1 = 2² * f(n-3) + 2 + 1 = 2² * f(n-3) + 2 + 1 = ?2² * (2f(n-4) + 1) = 2³ * f(n-4) + 2² ?+ 1 = .... ? ? ? ?// 不斷地展開 = 2^n-1 + 2^n-2 + ....+ 1

顯然時(shí)間復(fù)雜度為 O(2ⁿ)，很明顯指數(shù)級(jí)別的時(shí)間復(fù)雜度是不能接受的，漢諾塔非遞歸的解法比較復(fù)雜，大家可以去網(wǎng)上搜一下

進(jìn)階題

現(xiàn)實(shí)中大廠中的很多遞歸題都不會(huì)用上面這些相對(duì)比較容易理解的題，更加地是對(duì)遞歸問題進(jìn)行相應(yīng)地變形， 來看下面這道題

細(xì)胞分裂 有一個(gè)細(xì)胞 每一個(gè)小時(shí)分裂一次，一次分裂一個(gè)子細(xì)胞，第三個(gè)小時(shí)后會(huì)死亡。那么n個(gè)小時(shí)候有多少細(xì)胞？

照樣我們用前面的遞歸四步曲來解

1.定義問題的遞歸函數(shù)，明確函數(shù)的功能 我們定義以下函數(shù)為 n 個(gè)小時(shí)后的細(xì)胞數(shù)

public int allCells(int n) {
}

2.接下來尋找問題與子問題間的關(guān)系（即遞推公式） 首先我們看一下一個(gè)細(xì)胞出生到死亡后經(jīng)歷的所有細(xì)胞分裂過程

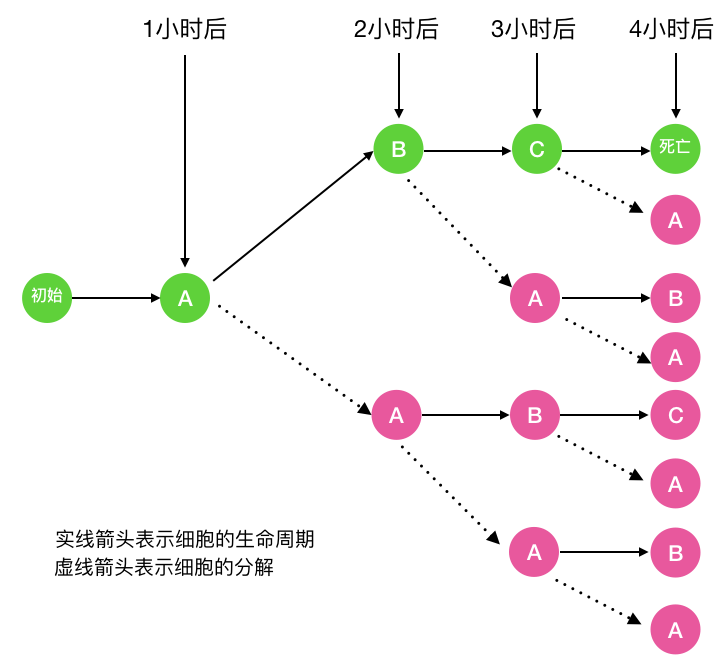
圖中的 A 代表細(xì)胞的初始態(tài), B代表幼年態(tài)(細(xì)胞分裂一次), C 代表成熟態(tài)(細(xì)胞分裂兩次)，C 再經(jīng)歷一小時(shí)后細(xì)胞死亡 以 f(n) 代表第 n 小時(shí)的細(xì)胞分解數(shù) f_a(n) 代表第 n 小時(shí)處于初始態(tài)的細(xì)胞數(shù), f_b(n) 代表第 n 小時(shí)處于幼年態(tài)的細(xì)胞數(shù) f_c(n) 代表第 n 小時(shí)處于成熟態(tài)的細(xì)胞數(shù) 則顯然 f(n) = ?f_a(n) ?+ f_b(n) ?+ f_c(n) 那么 f_a(n) 等于多少呢，以n = 4 （即一個(gè)細(xì)胞經(jīng)歷完整的生命周期）為例

仔細(xì)看上面的圖

可以看出 f_a(n) ?= f_a(n-1) + f_b(n-1) + f_c(n-1), 當(dāng) n = 1 時(shí)，顯然 f_a(1) = 1

f_b(n) 呢,看下圖可知 f_b(n) ?= f_a(n-1)。當(dāng) n = 1 時(shí) ?f_b(n) = 0

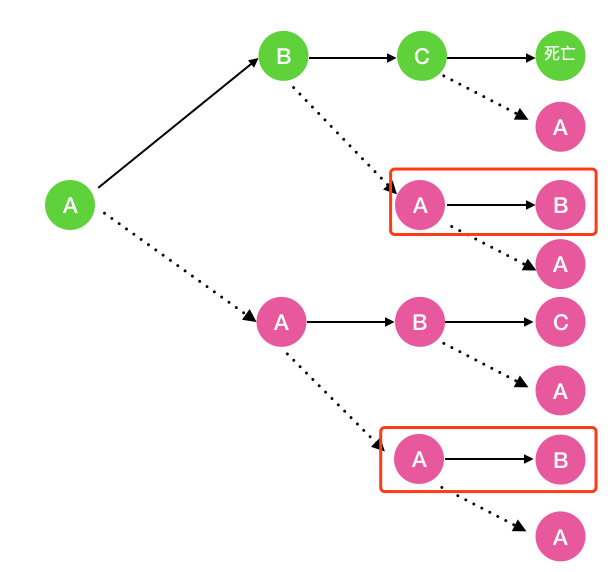
f_c(n) 呢,看下圖可知 ?f_c(n) ?= f_b(n-1)。當(dāng) n = 1,2 時(shí) f_c(n) = 0

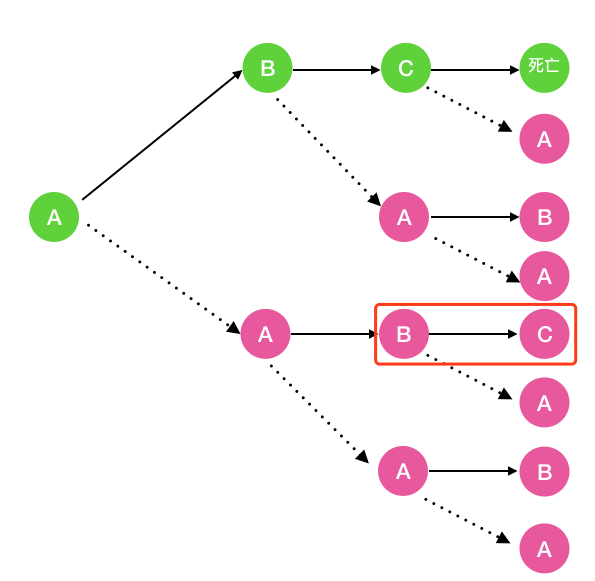
綜上， 我們得出的遞歸公式如下

f(n) = ?f_a(n) ?+ f_b(n) ?+ f_c(n)

3.根據(jù)以上遞歸公式我們補(bǔ)充一下函數(shù)的功能

public int allCells(int n) {
    return aCell(n) + bCell(n) + cCell(n);
}

/**
 * 第 n 小時(shí) a 狀態(tài)的細(xì)胞數(shù)
 */
public int aCell(int n) {
    if(n==1){
        return 1;
    }else{
        return aCell(n-1)+bCell(n-1)+cCell(n-1);
    }
}

/**
 * 第 n 小時(shí) b 狀態(tài)的細(xì)胞數(shù)
 */
public int bCell(int n) {
    if(n==1){
        return 0;
    }else{
        return aCell(n-1);
    }
}

/**
 * 第 n 小時(shí) c 狀態(tài)的細(xì)胞數(shù)
 */
public int cCell(int n) {
    if(n==1 || n==2){
        return 0;
    }else{
        return bCell(n-1);
    }
}

只要思路對(duì)了，將遞推公式轉(zhuǎn)成代碼就簡單多了，另一方面也告訴我們，可能一時(shí)的遞歸關(guān)系我們看不出來，此時(shí)可以借助于畫圖來觀察規(guī)律

4.求時(shí)間復(fù)雜度 由第二步的遞推公式我們知道 f(n) = 2aCell(n-1) + 2aCell(n-2) + aCell(n-3)

之前青蛙跳臺(tái)階時(shí)間復(fù)雜度是指數(shù)級(jí)別的，而這個(gè)方程式顯然比之前的遞推公式(f(n) = f(n-1) + f(n-2)) 更復(fù)雜的，所以顯然也是指數(shù)級(jí)別的

總結(jié)

大部分遞歸題其實(shí)還是有跡可尋的， 按照之前總結(jié)的解遞歸的四個(gè)步驟可以比較順利的解開遞歸題，一些比較復(fù)雜的遞歸題我們需要勤動(dòng)手，畫畫圖，觀察規(guī)律，這樣能幫助我們快速發(fā)現(xiàn)規(guī)律，得出遞歸公式，一旦知道了遞歸公式，將其轉(zhuǎn)成遞歸代碼就容易多了,很多大廠的遞歸考題并不能簡單地看出遞歸規(guī)律，往往會(huì)在遞歸的基礎(chǔ)上多加一些變形，不過萬遍不離其宗，我們多采用自頂向下的分析思維，多練習(xí)，相信遞歸不是什么難事

碼字不易，如覺得本文對(duì)您有幫助，點(diǎn)個(gè)「在看」再走唄!^_^