結(jié)合PyTorch和TensorFlow2 匯總理解損失函數(shù)

地址：https://www.zhihu.com/people/dengbocong

編輯 人工智能前沿講習(xí)

本文打算討論在深度學(xué)習(xí)中常用的十余種損失函數(shù)（含變種），結(jié)合PyTorch和TensorFlow2對(duì)其概念、公式及用途進(jìn)行闡述，希望能達(dá)到看過(guò)的伙伴對(duì)各種損失函數(shù)有個(gè)大致的了解以及使用。本文對(duì)原理只是淺嘗輒止，不進(jìn)行深挖，感興趣的伙伴可以針對(duì)每個(gè)部分深入翻閱資料。

使用版本：

• TensorFlow2.3

• PyTorch1.7.0

01

交叉熵?fù)p失（CrossEntropyLoss）

對(duì)于單事件的信息量而言，當(dāng)事件發(fā)生的概率越大時(shí)，信息量越小，需要明確的是，信息量是對(duì)于單個(gè)事件來(lái)說(shuō)的，實(shí)際事件存在很多種可能，所以這個(gè)時(shí)候熵就派上用場(chǎng)了，熵是表示隨機(jī)變量不確定的度量，是對(duì)所有可能發(fā)生的事件產(chǎn)生的信息量的期望。交叉熵用來(lái)描述兩個(gè)分布之間的差距，交叉熵越小，假設(shè)分布離真實(shí)分布越近，模型越好。

在分類(lèi)問(wèn)題模型中（不一定是二分類(lèi)），如邏輯回歸、神經(jīng)網(wǎng)絡(luò)等，在這些模型的最后通常會(huì)經(jīng)過(guò)一個(gè)sigmoid函數(shù)（softmax函數(shù)），輸出一個(gè)概率值（一組概率值），這個(gè)概率值反映了預(yù)測(cè)為正類(lèi)的可能性（一組概率值反應(yīng)了所有分類(lèi)的可能性）。而對(duì)于預(yù)測(cè)的概率分布和真實(shí)的概率分布之間，使用交叉熵來(lái)計(jì)算他們之間的差距，換句不嚴(yán)謹(jǐn)?shù)脑?huà)來(lái)說(shuō)，交叉熵?fù)p失函數(shù)的輸入，是softmax或者sigmoid函數(shù)的輸出。交叉熵?fù)p失可以從理論公式推導(dǎo)出幾個(gè)結(jié)論（優(yōu)點(diǎn)），具體公式推導(dǎo)不在這里詳細(xì)講解，如下：

• 預(yù)測(cè)的值跟目標(biāo)值越遠(yuǎn)時(shí)，參數(shù)調(diào)整就越快，收斂就越快；

• 不會(huì)陷入局部最優(yōu)解

交叉熵?fù)p失函數(shù)的標(biāo)準(zhǔn)形式（也就是二分類(lèi)交叉熵?fù)p失）如下:

其中，??表示樣本??的標(biāo)簽，正類(lèi)為1，負(fù)類(lèi)為0，??表示樣本??預(yù)測(cè)為正的概率。

多分類(lèi)交叉熵?fù)p失如下：

其中，??表示類(lèi)別的數(shù)量，??表示變量（0或1），如果該類(lèi)別和樣本??的類(lèi)別相同就是1，否則是0，??表示對(duì)于觀測(cè)樣本??屬于類(lèi)別??的預(yù)測(cè)概率。

Tensorflow：

• BinaryCrossentropy[1]：二分類(lèi)，經(jīng)常搭配Sigmoid使用

tf.keras.losses.BinaryCrossentropy(from_logits=False, label_smoothing=0, reduction=losses_utils.ReductionV2.AUTO, name='binary_crossentropy')參數(shù)：  from_logits：默認(rèn)False。為T(mén)rue，表示接收到了原始的logits，為False表示輸出層經(jīng)過(guò)了概率處理（softmax）  label_smoothing：[0,1]之間浮點(diǎn)值，加入噪聲，減少了真實(shí)樣本標(biāo)簽的類(lèi)別在計(jì)算損失函數(shù)時(shí)的權(quán)重，最終起到抑制過(guò)擬合的效果。  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• binary_crossentropy[2]

tf.keras.losses.binary_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0)參數(shù)：  from_logits：默認(rèn)False。為T(mén)rue，表示接收到了原始的logits，為False表示輸出層經(jīng)過(guò)了概率處理（softmax）  label_smoothing：[0,1]之間浮點(diǎn)值，加入噪聲，減少了真實(shí)樣本標(biāo)簽的類(lèi)別在計(jì)算損失函數(shù)時(shí)的權(quán)重，最終起到抑制過(guò)擬合的效果。

• CategoricalCrossentropy[3]：多分類(lèi)，經(jīng)常搭配Softmax使用

tf.keras.losses.CategoricalCrossentropy(from_logits=False, label_smoothing=0, reduction=losses_utils.ReductionV2.AUTO, name='categorical_crossentropy')參數(shù)：  from_logits：默認(rèn)False。為T(mén)rue，表示接收到了原始的logits，為False表示輸出層經(jīng)過(guò)了概率處理（softmax）  label_smoothing：[0,1]之間浮點(diǎn)值，加入噪聲，減少了真實(shí)樣本標(biāo)簽的類(lèi)別在計(jì)算損失函數(shù)時(shí)的權(quán)重，最終起到抑制過(guò)擬合的效果。  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• categorical_crossentropy[4]

tf.keras.losses.categorical_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0)參數(shù)：  from_logits：默認(rèn)False。為T(mén)rue，表示接收到了原始的logits，為False表示輸出層經(jīng)過(guò)了概率處理（softmax）  label_smoothing：[0,1]之間浮點(diǎn)值，加入噪聲，減少了真實(shí)樣本標(biāo)簽的類(lèi)別在計(jì)算損失函數(shù)時(shí)的權(quán)重，最終起到抑制過(guò)擬合的效果。

• SparseCategoricalCrossentropy[5]：多分類(lèi)，經(jīng)常搭配Softmax使用，和CategoricalCrossentropy不同之處在于，CategoricalCrossentropy是one-hot編碼，而SparseCategoricalCrossentropy使用一個(gè)位置整數(shù)表示類(lèi)別

tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False, reduction=losses_utils.ReductionV2.AUTO, name='sparse_categorical_crossentropy')參數(shù)：  from_logits：默認(rèn)False。為T(mén)rue，表示接收到了原始的logits，為False表示輸出層經(jīng)過(guò)了概率處理（softmax）  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• sparse_categorical_crossentropy[6]

tf.keras.losses.sparse_categorical_crossentropy(y_true, y_pred, from_logits=False, axis=-1)參數(shù)：  from_logits：默認(rèn)False。為T(mén)rue，表示接收到了原始的logits，為False表示輸出層經(jīng)過(guò)了概率處理（softmax）  axis：默認(rèn)是-1，計(jì)算交叉熵的維度

PyTorch：

• BCELoss[7]

torch.nn.BCELoss(weight: Optional[torch.Tensor] = None, size_average=None, reduce=None, reduction: str = 'mean')參數(shù)：  weight：每個(gè)分類(lèi)的縮放權(quán)重，傳入的大小必須和類(lèi)別數(shù)量一至  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction：string類(lèi)型，'none' | 'mean' | 'sum'三種參數(shù)值

• BCEWithLogitsLoss[8]：其實(shí)和TensorFlow是的`from_logits`參數(shù)很像，在BCELoss的基礎(chǔ)上合并了Sigmoid

torch.nn.BCEWithLogitsLoss(weight: Optional[torch.Tensor] = None, size_average=None, reduce=None, reduction: str = 'mean', pos_weight: Optional[torch.Tensor] = None)參數(shù)：  weight：每個(gè)分類(lèi)的縮放權(quán)重，傳入的大小必須和類(lèi)別數(shù)量一至  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction：string類(lèi)型，'none' | 'mean' | 'sum'三種參數(shù)值  pos_weight：正樣本的權(quán)重, 當(dāng)p>1，提高召回率，當(dāng)p<1，提高精確度。可達(dá)到權(quán)衡召回率(Recall)和精確度(Precision)的作用。

• CrossEntropyLoss[9]

torch.nn.CrossEntropyLoss(weight: Optional[torch.Tensor] = None, size_average=None, ignore_index: int = -100, reduce=None, reduction: str = 'mean')
參數(shù)：  weight：每個(gè)分類(lèi)的縮放權(quán)重，傳入的大小必須和類(lèi)別數(shù)量一至  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  ignore_index：忽略某一類(lèi)別，不計(jì)算其loss，其loss會(huì)為0，并且，在采用size_average時(shí)，不會(huì)計(jì)算那一類(lèi)的loss，除的時(shí)候的分母也不會(huì)統(tǒng)計(jì)那一類(lèi)的樣本  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction：string類(lèi)型，'none' | 'mean' | 'sum'三種參數(shù)值

02
KL散度

我們?cè)谟?jì)算預(yù)測(cè)和真實(shí)標(biāo)簽之間損失時(shí)，需要拉近他們分布之間的差距，即模型得到的預(yù)測(cè)分布應(yīng)該與數(shù)據(jù)的實(shí)際分布情況盡可能相近。KL散度(相對(duì)熵)是用來(lái)衡量?jī)蓚€(gè)概率分布之間的差異。模型需要得到最大似然估計(jì)，乘以負(fù)Log以后就相當(dāng)于求最小值，此時(shí)等價(jià)于求最小化KL散度(相對(duì)熵)。所以得到KL散度就得到了最大似然。又因?yàn)镵L散度中包含兩個(gè)部分，第一部分是交叉熵，第二部分是信息熵，即KL=交叉熵?信息熵。信息熵是消除不確定性所需信息量的度量，簡(jiǎn)單來(lái)說(shuō)就是真實(shí)的概率分布，而這部分是固定的，所以?xún)?yōu)化KL散度就是近似于優(yōu)化交叉熵。下面是KL散度的公式：

聯(lián)系上面的交叉熵，我們可以將公式簡(jiǎn)化為（KL散度 = 交叉熵 - 熵）：

監(jiān)督學(xué)習(xí)中，因?yàn)橛?xùn)練集中每個(gè)樣本的標(biāo)簽是已知的，此時(shí)標(biāo)簽和預(yù)測(cè)的標(biāo)簽之間的KL散度等價(jià)于交叉熵。

TensorFlow：

• KLD | kullback_leibler_divergence[10]

tf.keras.losses.KLD(y_true, y_pred)

• KLDivergence[11]

tf.keras.losses.KLDivergence(reduction=losses_utils.ReductionV2.AUTO, name='kl_divergence')參數(shù)：  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

Pytorch：

• KLDivLoss[12]

torch.nn.KLDivLoss(size_average=None, reduce=None, reduction: str = 'mean', log_target: bool = False)參數(shù)：  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction-三個(gè)值，none: 不使用約簡(jiǎn)；mean:返回loss和的平均值；sum:返回loss的和。默認(rèn)：mean  log_target：默認(rèn)False，指定是否在日志空間中傳遞目標(biāo)

03

平均絕對(duì)誤差（L1范數(shù)損失）

L1范數(shù)損失函數(shù)，也被稱(chēng)為最小絕對(duì)值偏差（LAD），最小絕對(duì)值誤差（LAE）。總的說(shuō)來(lái)，它是把目標(biāo)值??與估計(jì)值??的絕對(duì)差值的總和??最小化：

缺點(diǎn)：

• 梯度恒定，不論預(yù)測(cè)值是否接近真實(shí)值，這很容易導(dǎo)致發(fā)散，或者錯(cuò)過(guò)極值點(diǎn)。

• 導(dǎo)數(shù)不連續(xù)，導(dǎo)致求解困難。這也是L1損失函數(shù)不廣泛使用的主要原因。

優(yōu)點(diǎn)：

• 收斂速度比L2損失函數(shù)要快，這是通過(guò)對(duì)比函數(shù)圖像得出來(lái)的，L1能提供更大且穩(wěn)定的梯度。

• 對(duì)異常的離群點(diǎn)有更好的魯棒性，下面會(huì)以例子證實(shí)。

TensorFlow：

• MAE | mean_absolute_error[13]

tf.keras.losses.MAE(y_true, y_pred)

• MeanAbsoluteError[14]

tf.keras.losses.MeanAbsoluteError(reduction=losses_utils.ReductionV2.AUTO, name='mean_absolute_error')參數(shù)：  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• MeanAbsolutePercentageError[15]：平均絕對(duì)百分比誤差

tf.keras.losses.MeanAbsolutePercentageError(reduction=losses_utils.ReductionV2.AUTO, name='mean_absolute_percentage_error')公式：loss = 100 * abs(y_true - y_pred) / y_true參數(shù)：  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• MAPE | mean_absolute_percentage_error[16]：平均絕對(duì)百分比誤差

tf.keras.losses.MAPE(y_true, y_pred)公式：loss = 100 * mean(abs((y_true - y_pred) / y_true), axis=-1)

• Huber[17]

tf.keras.losses.Huber(delta=1.0, reduction=losses_utils.ReductionV2.AUTO, name='huber_loss')公式：error = y_true - y_pred參數(shù)：  delta：float類(lèi)型，Huber損失函數(shù)從二次變?yōu)榫€性的點(diǎn)。  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

PyTorch：

• L1Loss[18]

torch.nn.L1Loss(size_average=None, reduce=None, reduction: str = 'mean')參數(shù)：  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction-三個(gè)值，none: 不使用約簡(jiǎn)；mean:返回loss和的平均值；sum:返回loss的和。默認(rèn)：mean

• l1_loss[19]

torch.nn.functional.l1_loss(input, target, size_average=None, reduce=None, reduction='mean')

• SmoothL1Loss[20]：平滑版L1損失，也被稱(chēng)為 Huber 損失函數(shù)。

其中，當(dāng)??時(shí)，??，否則?

torch.nn.SmoothL1Loss(size_average=None, reduce=None, reduction: str = 'mean', beta: float = 1.0)參數(shù)：  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction-三個(gè)值，none: 不使用約簡(jiǎn)；mean:返回loss和的平均值；sum:返回loss的和。默認(rèn)：mean  beta：默認(rèn)為1，指定在L1和L2損耗之間切換的閾值

• smooth_l1_loss[21]

torch.nn.functional.smooth_l1_loss(input, target, size_average=None, reduce=None, reduction='mean', beta=1.0)

04

均方誤差損失（L2范數(shù)損失）

L2范數(shù)損失函數(shù)，也被稱(chēng)為最小平方誤差（LSE）。總的來(lái)說(shuō)，它是把目標(biāo)值??與估計(jì)值??的差值的平方和??最小化：

缺點(diǎn)：

• 收斂速度比L1慢，因?yàn)樘荻葧?huì)隨著預(yù)測(cè)值接近真實(shí)值而不斷減小。

• 對(duì)異常數(shù)據(jù)比L1敏感，這是平方項(xiàng)引起的，異常數(shù)據(jù)會(huì)引起很大的損失。

優(yōu)點(diǎn)：

• 它使訓(xùn)練更容易，因?yàn)樗奶荻入S著預(yù)測(cè)值接近真實(shí)值而不斷減小，那么它不會(huì)輕易錯(cuò)過(guò)極值點(diǎn)，但也容易陷入局部最優(yōu)。

• 它的導(dǎo)數(shù)具有封閉解，優(yōu)化和編程非常容易，所以很多回歸任務(wù)都是用MSE作為損失函數(shù)。

TensorFlow：

• MeanSquaredError[22]

tf.keras.losses.MeanSquaredError(reduction=losses_utils.ReductionV2.AUTO, name='mean_squared_error')公式：loss = square(y_true - y_pred)參數(shù)：  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• MSE | mean_squared_error[23]

tf.keras.losses.MSE(y_true, y_pred)公式：loss = mean(square(y_true - y_pred), axis=-1)

• MeanSquaredLogarithmicError[24]

tf.keras.losses.MeanSquaredLogarithmicError(reduction=losses_utils.ReductionV2.AUTO, name='mean_squared_logarithmic_error')公式：loss = square(log(y_true + 1.) - log(y_pred + 1.))參數(shù)：  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• MSLE | mean_squared_logarithmic_error[25]

tf.keras.losses.MSLE(y_true, y_pred)公式：loss = mean(square(log(y_true + 1) - log(y_pred + 1)), axis=-1)

PyTorch：

• MSELoss[26]

torch.nn.MSELoss(size_average=None, reduce=None, reduction: str = 'mean')參數(shù)：  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction-三個(gè)值，none: 不使用約簡(jiǎn)；mean:返回loss和的平均值；sum:返回loss的和。默認(rèn)：mean

• mse_loss[27]

torch.nn.functional.mse_loss(input, target, size_average=None, reduce=None, reduction='mean')

05

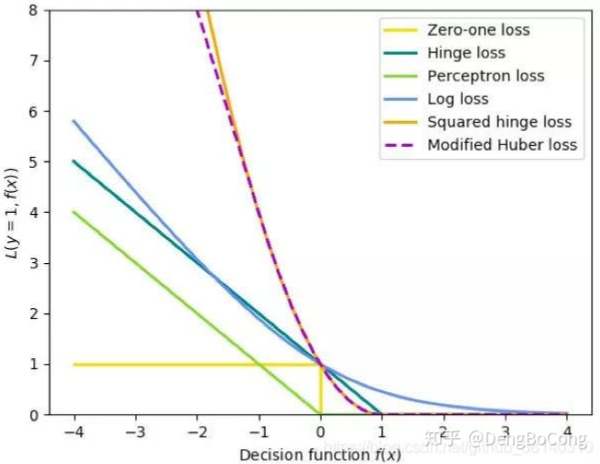
Hinge loss

有人把hinge loss稱(chēng)為鉸鏈損失函數(shù)，它可用于“最大間隔(max-margin)”分類(lèi)，其最著名的應(yīng)用是作為SVM的損失函數(shù)。hinge loss專(zhuān)用于二分類(lèi)問(wèn)題，標(biāo)簽值??，預(yù)測(cè)值??。二分類(lèi)問(wèn)題的目標(biāo)函數(shù)的要求如下：當(dāng)??大于等于??或者小于等于??時(shí)，都是分類(lèi)器確定的分類(lèi)結(jié)果，此時(shí)的損失函數(shù)loss為0。而當(dāng)預(yù)測(cè)值??時(shí)，分類(lèi)器對(duì)分類(lèi)結(jié)果不確定，loss不為0。顯然，當(dāng)??時(shí)，loss達(dá)到最大值。對(duì)于輸出??，當(dāng)前??的損失為：

擴(kuò)展到多分類(lèi)問(wèn)題上就需要多加一個(gè)邊界值，然后疊加起來(lái)。公式如下：

Tensorflow：

• CategoricalHinge[28]

tf.keras.losses.CategoricalHinge(reduction=losses_utils.ReductionV2.AUTO, name='categorical_hinge')公式：loss = maximum(neg - pos + 1, 0) where neg=maximum((1-y_true)*y_pred) and pos=sum(y_true*y_pred)參數(shù)：  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• categorical_hinge[29]

tf.keras.losses.categorical_hinge(y_true, y_pred)公式：loss = maximum(neg - pos + 1, 0) where neg=maximum((1-y_true)*y_pred) and pos=sum(y_true*y_pred)

• Hinge[30]

tf.keras.losses.Hinge(    reduction=losses_utils.ReductionV2.AUTO, name='hinge')公式：loss = maximum(1 - y_true * y_pred, 0)，y_true值應(yīng)為-1或1。如果提供了二進(jìn)制（0或1）標(biāo)簽，會(huì)將其轉(zhuǎn)換為-1或1參數(shù)：  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• hinge[31]

tf.keras.losses.hinge(y_true, y_pred)公式：loss = mean(maximum(1 - y_true * y_pred, 0), axis=-1)

• SquaredHinge[32]

tf.keras.losses.SquaredHinge(    reduction=losses_utils.ReductionV2.AUTO, name='squared_hinge')公式：loss = square(maximum(1 - y_true * y_pred, 0))，y_true值應(yīng)為-1或1。如果提供了二進(jìn)制（0或1）標(biāo)簽，會(huì)將其轉(zhuǎn)換為-1或1。參數(shù)：  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• squared_hinge[33]

tf.keras.losses.squared_hinge(y_true, y_pred)公式：loss = mean(square(maximum(1 - y_true * y_pred, 0)), axis=-1)

PyTorch：

• HingeEmbeddingLoss[34]：當(dāng)??時(shí)，??，當(dāng)??時(shí)，?

torch.nn.HingeEmbeddingLoss(margin: float = 1.0, size_average=None, reduce=None, reduction: str = 'mean')參數(shù)：  margin：float類(lèi)型，默認(rèn)為1.  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction-三個(gè)值，none: 不使用約簡(jiǎn)；mean:返回loss和的平均值；sum:返回loss的和。默認(rèn)：mean

06

余弦相似度

余弦相似度是機(jī)器學(xué)習(xí)中的一個(gè)重要概念，在Mahout等MLlib中有幾種常用的相似度計(jì)算方法，如歐氏相似度，皮爾遜相似度，余弦相似度，Tanimoto相似度等。其中，余弦相似度是其中重要的一種。余弦相似度用向量空間中兩個(gè)向量夾角的余弦值作為衡量?jī)蓚€(gè)個(gè)體間差異的大小。相比距離度量，余弦相似度更加注重兩個(gè)向量在方向上的差異，而非距離或長(zhǎng)度上。

余弦相似度更多的是從方向上區(qū)分差異，而對(duì)絕對(duì)的數(shù)值不敏感，更多的用于使用用戶(hù)對(duì)內(nèi)容評(píng)分來(lái)區(qū)分用戶(hù)興趣的相似度和差異，同時(shí)修正了用戶(hù)間可能存在的度量標(biāo)準(zhǔn)不統(tǒng)一的問(wèn)題（因?yàn)橛嘞蚁嗨贫葘?duì)絕對(duì)數(shù)值不敏感），公式如下：

Tensorflow：

• CosineSimilarity[35]：請(qǐng)注意，所得值是介于-1和0之間的負(fù)數(shù)，其中0表示正交性，而接近-1的值表示更大的相似性。如果y_true或y_pred是零向量，則余弦相似度將為0，而與預(yù)測(cè)值和目標(biāo)值之間的接近程度無(wú)關(guān)。

tf.keras.losses.CosineSimilarity(axis=-1, reduction=losses_utils.ReductionV2.AUTO, name='cosine_similarity')公式：loss = -sum(l2_norm(y_true) * l2_norm(y_pred))參數(shù)：  axis：默認(rèn)-1，沿其計(jì)算余弦相似度的維  reduction：傳入tf.keras.losses.Reduction類(lèi)型值，默認(rèn)AUTO，定義對(duì)損失的計(jì)算方式。

• cosine_similarity[36]

tf.keras.losses.cosine_similarity(y_true, y_pred, axis=-1)公式：loss = -sum(l2_norm(y_true) * l2_norm(y_pred))參數(shù)：  axis：默認(rèn)-1，沿其計(jì)算余弦相似度的維

PyTorch：

• CosineEmbeddingLoss[37]：當(dāng)??時(shí)，??，當(dāng)??時(shí)，?

torch.nn.CosineEmbeddingLoss(margin: float = 0.0, size_average=None, reduce=None, reduction: str = 'mean')參數(shù)：  margin：float類(lèi)型，應(yīng)為-1到1之間的數(shù)字，建議為0到0.5，默認(rèn)值為0  size_average：bool類(lèi)型，為T(mén)rue時(shí)，返回的loss為平均值，為False時(shí)，返回的各樣本的loss之和  reduce：bool類(lèi)型，返回值是否為標(biāo)量，默認(rèn)為T(mén)rue  reduction-三個(gè)值，none: 不使用約簡(jiǎn)；mean:返回loss和的平均值；sum:返回loss的和。默認(rèn)：mean

07

總結(jié)

上面這些損失函數(shù)是我們?cè)谌粘Ｖ薪?jīng)常使用到的，我將TensorFlow和PyTorch相關(guān)的API都貼出來(lái)了，也方便查看，可以作為一個(gè)手冊(cè)文章，需要的時(shí)候點(diǎn)出來(lái)看一下。還有一些其他的損失函數(shù)，后續(xù)也會(huì)都加進(jìn)來(lái)。

外鏈地址：

[1] https://www.tensorflow.org/api_docs/python/tf/keras/losses/BinaryCrossentropy

[2] https://www.tensorflow.org/api_docs/python/tf/keras/losses/binary_crossentropy

[3] https://www.tensorflow.org/api_docs/python/tf/keras/losses/CategoricalCrossentropy

[4] https://www.tensorflow.org/api_docs/python/tf/keras/losses/categorical_crossentropy

[5] https://www.tensorflow.org/api_docs/python/tf/keras/losses/SparseCategoricalCrossentropy

[6] https://www.tensorflow.org/api_docs/python/tf/keras/losses/sparse_categorical_crossentropy

[7] https://pytorch.org/docs/stable/generated/torch.nn.BCELoss.html

[8] https://pytorch.org/docs/stable/generated/torch.nn.BCEWithLogitsLoss.html

[9] https://pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html

[10] https://www.tensorflow.org/api_docs/python/tf/keras/losses/KLD

[11] https://www.tensorflow.org/api_docs/python/tf/keras/losses/KLDivergence

[12] https://pytorch.org/docs/stable/generated/torch.nn.KLDivLoss.html

[13] https://www.tensorflow.org/api_docs/python/tf/keras/losses/MAE

[14] https://www.tensorflow.org/api_docs/python/tf/keras/losses/MeanAbsoluteError

[15] https://www.tensorflow.org/api_docs/python/tf/keras/losses/MeanAbsolutePercentageError

[16] https://www.tensorflow.org/api_docs/python/tf/keras/losses/MAPE

[17] https://www.tensorflow.org/api_docs/python/tf/keras/losses/Huber

[18] https://pytorch.org/docs/stable/generated/torch.nn.L1Loss.html

[19] https://pytorch.org/docs/stable/nn.functional.html?highlight=loss#torch.nn.functional.l1_loss

[20] https://pytorch.org/docs/stable/generated/torch.nn.SmoothL1Loss.html

[21] https://pytorch.org/docs/stable/nn.functional.html?highlight=loss#torch.nn.functional.smooth_l1_loss

[22] https://www.tensorflow.org/api_docs/python/tf/keras/losses/MeanSquaredError

[23] https://www.tensorflow.org/api_docs/python/tf/keras/losses/MSE

[24] https://www.tensorflow.org/api_docs/python/tf/keras/losses/MeanSquaredLogarithmicError

[25] https://www.tensorflow.org/api_docs/python/tf/keras/losses/MSLE

[26] https://pytorch.org/docs/stable/generated/torch.nn.MSELoss.html

[27] https://pytorch.org/docs/stable/nn.functional.html?highlight=loss#torch.nn.functional.mse_loss

[28] https://www.tensorflow.org/api_docs/python/tf/keras/losses/CategoricalHinge

[29] https://www.tensorflow.org/api_docs/python/tf/keras/losses/categorical_hinge

[30] https://www.tensorflow.org/api_docs/python/tf/keras/losses/Hinge

[31] https://www.tensorflow.org/api_docs/python/tf/keras/losses/hinge

[32] https://www.tensorflow.org/api_docs/python/tf/keras/losses/SquaredHinge

[33] https://www.tensorflow.org/api_docs/python/tf/keras/losses/squared_hinge

[34] https://pytorch.org/docs/stable/generated/torch.nn.HingeEmbeddingLoss.html

[35] https://www.tensorflow.org/api_docs/python/tf/keras/losses/CosineSimilarity

[36] https://www.tensorflow.org/api_docs/python/tf/keras/losses/cosine_similarity

[37] https://pytorch.org/docs/stable/generated/torch.nn.CosineEmbeddingLoss.html

本文目的在于學(xué)術(shù)交流，并不代表本公眾號(hào)贊同其觀點(diǎn)或?qū)ζ鋬?nèi)容真實(shí)性負(fù)責(zé)，版權(quán)歸原作者所有，如有侵權(quán)請(qǐng)告知?jiǎng)h除。

下載1：速查表

在「AI算法與圖像處理」公眾號(hào)后臺(tái)回復(fù)：速查表，即可下載21張 AI相關(guān)的查找表，包括 python基礎(chǔ)，線性代數(shù)，scipy科學(xué)計(jì)算，numpy，kears，tensorflow等等


下載2 CVPR2020

在「AI算法與圖像處理」公眾號(hào)后臺(tái)回復(fù)：CVPR2020，即可下載1467篇CVPR?2020論文
個(gè)人微信（如果沒(méi)有備注不拉群！）
請(qǐng)注明：地區(qū)+學(xué)校/企業(yè)+研究方向+昵稱(chēng)

覺(jué)得不錯(cuò)就點(diǎn)亮在看吧