色先锋AV,韩国自拍偷拍一区二区,一本道精品在线播放,性色av中文字幕,日韩一级特黄A片免费观,日本免费黄视频,黄片在现免费观看,www.97

點擊下面卡片關注，”AI算法與圖像處理”

最新CV成果，火速送達

〇.前言

(為了減少小編的工作量，文中部分較為簡單的公式使用上標下標的方式來呈現(xiàn)。如給讀者閱讀帶來不便，作者非常抱歉。)

深度學習可解釋性是目前深度學習的主流研究方向之一，更被廣泛認為是下一代人工智能技術的關鍵一環(huán)。我們可以想象，可解釋性問題一旦取得了突破，將立馬對整個深度學習的科研及應用產(chǎn)生全局性的影響，大大促進AI在醫(yī)療、安全、國防、金融等重要領域的應用。因此，無論是做什么方面研究，方法學創(chuàng)新還是應用創(chuàng)新，對于人工智能研究者來說，關注并且了解AI可解釋性方面的最新進展是十分必要的。本文以最新發(fā)表的可解釋性綜述（On Interpretability of Artificial Neural Networks: A Survey，https://ieeexplore.ieee.org/document/9380482）為基礎，全面系統(tǒng)地介紹可解釋性的最新進展，感興趣的讀者也可以直接訪問我們的talk（https://www.youtube.com/watch?v=o6AvW0Eqc3g）。

一.介紹

1. 綜述的評價和比較

毫無疑問，近幾年來已經(jīng)有若干篇深度學習可解釋性綜述出現(xiàn)。比如

Q. Zhang and S. C. Zhu [1] 的《Visual interpretability for deep learning: a survey》；

S. Chakraborty et al. [2]的《Interpretability of deep learning models: a survey of results》

M. Du et al. [3]的《Techniques for interpretable machine learning》；

L. H. Gilpin et al. [4]的“Explaining explanations: An overview of interpretability of machine learning》；R. Guidotti et al. [5]的《A survey of methods for explaining black box models》；

A. Adadi and M. Berrada [6]的《Peeking inside the black-box: A survey on Explainable Artificial Intelligence (XAI) 》。

盡管這些綜述做了很棒的工作，但是他們在全面性和細致性上仍然有相當?shù)奶嵘臻g。Q. Zhang and S. C. Zhu的文章主要集中在視覺可解釋性，比如特征可視化、熱圖等等。S. Chakraborty et al. 的文章全面性稍不足：作為綜述，它只引用了四十幾篇文章，無法反映出可解釋性的全貌。L. H. Gilpin et al. 集中在事后可解釋性上，即模型已經(jīng)訓練好了之后再去解釋它，而忽略了從頭打造可解釋性這一重要方向。R. Guidotti et al. 和A. Adadi and M. Berrada的綜述講的是整個AI方法的可解釋性，里面不止介紹神經(jīng)網(wǎng)絡，還有諸多AI模型。因此，這兩個綜述在神經(jīng)網(wǎng)絡上著墨相對有限，也因此遺漏了一些神經(jīng)網(wǎng)絡可解釋性的重要方向，比如運用先進的數(shù)理方法來解釋神經(jīng)網(wǎng)絡。相比之下，最新的這個綜述《On Interpretability of Artificial Neural Networks: A Survey》同時兼顧了全面性和細致性。這篇綜述總共引用了兩百多篇文獻，對各類方法有教學性質的介紹，同時也實現(xiàn)了若干代表性可解釋性方法并公開了代碼。

[1] Q. Zhang and S. C. Zhu, “Visual interpretability for deep learning: a survey,” Frontiers of Information Technology & Electronic Engineering, vol. 19, no. 1, pp. 27-39, 2018.

[2] S. Chakraborty, “Interpretability of deep learning models: a survey of results,” IEEE Smart World, Ubiquitous Intelligence & Computing, Advanced & Trusted Computed, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation, 2017.

[3] M. Du, N. Liu and X. Hu, “Techniques for interpretable machine learning,” arXiv preprint, arXiv:1808.00033, 2018.

[4] L. H. Gilpin, D. Bau, B. Z. Yuan, A. Bajwa, M. Specter, L. Kagal, “Explaining explanations: An overview of interpretability of machine learning,” In DSAA, pp. 80-89, 2018.

[5] R. Guidotti, A. Monreale, S. Ruggieri, F. Turini, F. Giannotti & D. Pedreschi, “A survey of methods for explaining black box models,” ACM computing surveys (CSUR), vol. 51, no. 5, pp. 93, 2019.

[6] A. Adadi and M. Berrada, “Peeking inside the black-box: A survey on Explainable Artificial Intelligence (XAI),” IEEE Access, vol. 6, pp. 52138-52160, 2018.

2. 可解釋性的含義

盡管可解釋性這個詞經(jīng)常用到，但是到底可解釋性的含義是什么，大家的認知還是模糊的。Lipton[1]總結了可解釋性的三層含義：

Simulatability: 指的是對整個模型的高層次的理解，比如一個線性分類器就是完全透明、可解釋的。在九十年代的一篇Science論文[2]中，Poggio提出了徑向基函數(shù)網(wǎng)絡的解釋：一個單隱含層的徑向基函數(shù)網(wǎng)絡可以是插值問題的一個解，徑向基函數(shù)的形狀是由一個正則項控制的。由此建立了對徑向基網(wǎng)絡的高層次理解。

Decomposability: 指的是通過了解一個網(wǎng)絡每個組分的作用來達到理解一個模型的作用。這正是工程中常見的模塊化思想。在機器學習里面，決策樹的可解釋性較強，從輸入到輸出，節(jié)點一路走下來，每一個節(jié)點和分支都有一個特定的功能，所以理解決策樹就相對比較簡單。

Algorithmic transparency: 指的是理解網(wǎng)絡的訓練和動態(tài)行為。

[1] Z. C. Lipton, “The mythos of model interpretability,” Queue, vol. 16, no. 3, pp. 31–57, 2018.

[2] T. Poggio and F. Girosi, “Regularization algorithms for learning that are equivalent to multilayer networks,” Science, vol. 247, no. 4945, pp. 978–982, 1990.

3. 可解釋性的困難之處

（1）人類局限性（Human Limitation）。在許多情況下，人的專業(yè)知識是極度缺乏的。當我們自身都缺乏某一領域專業(yè)知識的時候，我們又該如何來理解神經(jīng)網(wǎng)絡在這一個領域的應用呢？舉一個極端的例子，在Fan et al. [1]中，神經(jīng)網(wǎng)絡被用來預測偽隨機事件。首先一串隨機數(shù)被生成，作者將前100000位數(shù)字作為神經(jīng)網(wǎng)絡輸入，100001位數(shù)字作為神經(jīng)網(wǎng)絡的輸出。預測的準確度達到了3。據(jù)此作者猜想，神經(jīng)網(wǎng)絡可以用來驗證上帝是否投擲色子這一物理學經(jīng)典問題，因為神經(jīng)網(wǎng)絡的高度敏感性和學習能力可以來判定一串隨機數(shù)是真隨機還是偽隨機。可以想象，對這樣的網(wǎng)絡進行可解釋性的研究是非常困難的，因為隨機數(shù)背后是不是隱含著物理規(guī)律（量子力學背后是否有更深刻的理論）現(xiàn)在世界上沒有幾個人搞的清楚。

（2）商業(yè)阻礙（Commercial Barrier）[2]。首先，如果商業(yè)公司使用的是一個完全透明的神經(jīng)網(wǎng)絡模型來做應用，那么公司肯定就無法賺錢了。第二，模型的不可解釋性在一定程度上可以保護公司的知識產(chǎn)權。如果一個模型可解釋性很強，那么競爭者就有可能通過逆向工程把模型給做出來，就會損害公司的利益。第三，打造一個可解釋性模型會造成額外的工作，有些工程師并不愿意這樣做。

（3）數(shù)據(jù)異質化（Data Wildness）。一個真實的數(shù)據(jù)集可能包含著各種各樣你想象不到的數(shù)據(jù)。比如一個醫(yī)療數(shù)據(jù)集可能包括以下數(shù)據(jù)：臨床數(shù)據(jù)，分子數(shù)據(jù)，圖像和生物測量信號，實驗室化驗結果，病患口述結果等等。此外，數(shù)據(jù)的維度也很高，一個很小的圖片也能達到幾百上萬維。在高維空間發(fā)展可解釋性比在低維空間要難的多。其實，我們對低維情形的網(wǎng)絡運行機理已經(jīng)有了相當?shù)牧私狻?/p>

（4）算法復雜性（Algorithmic Complexity）。深度神經(jīng)網(wǎng)絡不僅使用各種各樣的非線性組件，并且參數(shù)量還特別巨大，往往形成過參數(shù)化的情況。甚至意料之外的情況也會出現(xiàn)，比如，九十年代一篇論文的證明結果：RNN可能會產(chǎn)生混沌現(xiàn)象[3]。

[1] F. Fan and G. Wang, “Learning from pseudo-randomness with an artificial neural network–does god play pseudo-dice?” IEEE Access, vol. 6, pp. 22987–22992, 2018.

[2] C. Rudin, “Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead,” Nat. Mach. Intell., vol. 1, no. 5, pp. 206–215, 2019.

[3] H. L. Van der Maas, P. F. Verschure, and P. C. Molenaar, “A note on chaotic behavior in simple neural networks,” Neural Netw., vol. 3, no. 1, pp. 119–122, 1990.

4. 可解釋性研究好壞的評價

接下來一個問題是，評估可解釋性方法質量的標準是什么？由于現(xiàn)有的評估方法還不成熟，因此我們提出了五種通用且定義明確的經(jīng)驗法則：精準度，一致性，完整性，普遍性和實用性。

精準度：精準度是指解釋方法的準確性。一個可解釋性算法是否只限于定性描述還是存在定量分析？通常，定量解釋方法比定性解釋方法更為可取。

一致性：一致性表明解釋中沒有任何矛盾。對于多個相似的樣本，好的解釋應該產(chǎn)生一致的答案。此外，解釋方法應符合真實模型的預測。例如，基于代理的方法是利用它們對原始模型的復制準確程度進行評估的。

完整性：從數(shù)學上講，神經(jīng)網(wǎng)絡是要學習最適合數(shù)據(jù)的映射。一個好的解釋方法應該顯示出在最大數(shù)量的數(shù)據(jù)實例和數(shù)據(jù)類型方面的有效性，而不是只對某些數(shù)據(jù)有效。

通用性：隨著深度學習的飛速發(fā)展，深度學習方法庫已大大豐富。這種多樣化的深度學習模型在各種任務中扮演著重要的角色。我們是否可以開發(fā)一種通用解釋器，該解釋器可以解釋盡可能多的模型以節(jié)省人工和時間？但由于模型之間的高度可變性，通用解釋器在技術上非常具有挑戰(zhàn)性。

實用性：對神經(jīng)網(wǎng)絡的了解使我們獲得了什么？除了獲得從業(yè)者和用戶的信任之外，可解釋性的成果還可以是對網(wǎng)絡設計，訓練等的深刻見解。由于其黑盒性質，使用神經(jīng)網(wǎng)絡在很大程度上是一個反復試驗的過程，有時會產(chǎn)生矛盾的直覺。可解釋性的增強應當要幫助我們理清這些矛盾之處。

二.趨勢和分類

1. 趨勢

2020年9月22日，我們將搜索詞“Deep Learning Interpretability”, “Neural Network Interpretability”, “Explainable Neural Network”和 “Explainable Deep Learning”輸入到Web of Science中，時間范圍為2000年至2019年。圖1中繪制了相對于年份的文章數(shù)量的變化，該圖清楚地顯示了神經(jīng)網(wǎng)絡可解釋性領域的指數(shù)增長趨勢。

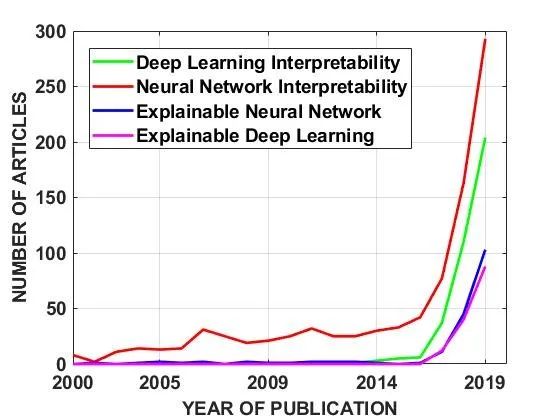
圖1. 深度學習可解釋性論文的指數(shù)增長趨勢

2. 方法的分類

根據(jù)我們對論文的調查，我們將可解釋性論文進行如下分類。

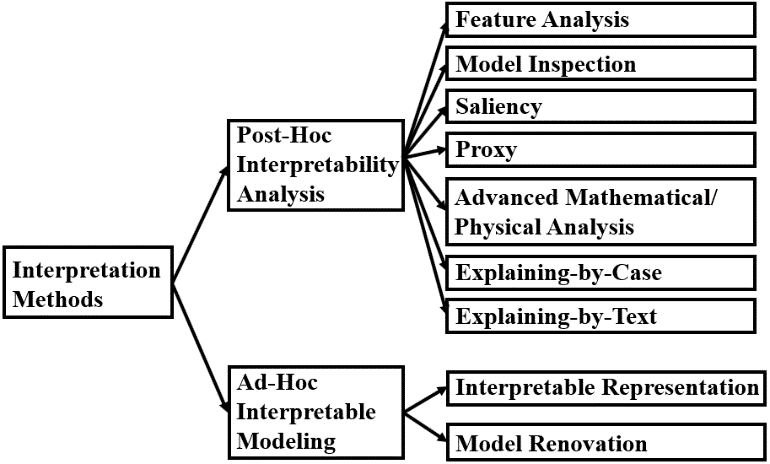
圖2. 深度學習可解釋性論文的分類法

具體來說：首先可以分成兩大類：“事后可解釋性分析”和“事前可解釋性建模”。前者是模型已經(jīng)訓練好了，然后去解釋，后者是從頭設計可解釋性的模型。進一步，“事后可解釋性分析”可以分成七個子類：特征分析（Feature Analysis）、模型檢查（Model Inspection）、顯著表征（Saliency）、代理模型（Proxy）、先進數(shù)理（Advanced Math/Physics Method）、案例解釋（Explaining-by-Case）、文本解釋（Explaining-by-Text）。“事前可解釋性建模”可以再分成可解釋表示（Interpretable Representation）、模型修繕（Model Renovation）。下面我們逐個進行解釋。

2.1 事后可解釋性分析

事后可解釋性是在充分學習模型之后進行的。事后方法的一個主要優(yōu)點是，由于預測和解釋是兩個獨立的過程而不會相互干擾，因此不需要為了追求預測性能來犧牲可解釋性。但是，事后解釋通常并不完全忠實于原始模型。因為如果解釋與原始模型相比100％準確，那么它就跟原始模型一樣了。因此，此類別中的任何解釋方法或多或少都是不準確的。糟糕的是，我們常常不知道時哪里出現(xiàn)了細微差別，因此我們很難完全信任事后解釋方法。

特征分析（Feature Analysis）技術的重點是比較、分析和可視化神經(jīng)網(wǎng)絡的神經(jīng)元和層的特征。通過特征分析，可以識別敏感特征及其處理方式，從而可以在一定程度上解釋模型的原理。特征分析技術可以應用于任何神經(jīng)網(wǎng)絡，并提供有關網(wǎng)絡學習了哪些特征的定性見解。但是，這些技術缺乏深入，嚴格和統(tǒng)一的理解，因此很難用來反饋提高神經(jīng)網(wǎng)絡的可解釋性。

模型檢查（Model Inspection）方法使用外部算法，通過系統(tǒng)地提取神經(jīng)網(wǎng)絡內部工作機制的重要結構和參數(shù)信息，來深入研究神經(jīng)網(wǎng)絡。與定性分析相比，此類中的方法在技術上更具可靠性，比如統(tǒng)計分析工具介入到了對模型的分析。通過模型檢查方法獲得的信息更值得信賴和也更有用。在一個研究中[1]，研究人員發(fā)現(xiàn)了重要的數(shù)據(jù)路由路徑。使用這種數(shù)據(jù)路由路徑，可以將模型準確地壓縮為緊湊的模型。

顯著表征（Saliency）方法確定輸入數(shù)據(jù)的哪些屬性與模型的預測或潛在表示最相關。在此類別中，需要進行人工檢查來確定顯著性圖是否合理。在大多數(shù)情況下，顯著性圖很有用。例如，如果北極熊總是與雪或冰出現(xiàn)在同一張圖片中，則該模型可能會選擇用雪或冰的信息來檢測北極熊，而不是使用了北極熊的真實特征。使用顯著性圖，我們就可以發(fā)現(xiàn)并避免此問題。顯著性方法在可解釋性研究中很流行，但是，大量隨機測試顯示，某些顯著性方法可以獨立于模型且不依賴于數(shù)據(jù)[2]，即某些方法提供的顯著性圖與邊緣檢測器產(chǎn)生的結果高度相似。這是有問題的，因為這意味著那些顯著性方法無法找到解釋模型預測的輸入的真實屬性。在這種情況下，應開發(fā)與模型相關和與數(shù)據(jù)相關的顯著性方法。

代理模型（Proxy）方法構造了一個更簡單，更易解釋的代理模型。理想情況下，它與經(jīng)過訓練的，大型，復雜和黑盒子的深度學習模型非常相似。代理方法可以是部分空間中的局部方法，也可以是整個空間中的全局方法。經(jīng)常使用的代理模型包括決策樹，規(guī)則系統(tǒng)等。代理方法的弱點是構建代理模型需要付出額外成本。

先進數(shù)理（Advanced Math/Physics Method）將神經(jīng)網(wǎng)絡置于數(shù)學/物理框架中，便可以使用高級的數(shù)學/物理工具來了解神經(jīng)網(wǎng)絡的機制。此類別涵蓋了深度學習的理論進展，包括非凸優(yōu)化，表示能力和泛化能力。本類別中的方法可能會出現(xiàn)一種情況：為了建立合理的解釋，有時會做出不切實際的假設以促進理論分析。

案例解釋（Explaining-by-Case）方法與基于案例的推理相似[3]。人們喜歡例子。一個人可能不會沉迷于產(chǎn)品的統(tǒng)計數(shù)字，但會喜歡看其他用戶使用該產(chǎn)品的經(jīng)驗。基于案例的深度學習解釋也是這樣的想法。個案解釋方法提供了具有代表性的示例，這些示例捕獲了模型的特質。此類中的方法有趣且啟發(fā)人心。但是，這種做法更像是一種健全性檢查，而不是一般性的解釋，因為從選定的查詢案例中了解的關于神經(jīng)網(wǎng)絡內部工作的信息不多。

文本解釋（Explaining-by-Text）方法在圖像語言聯(lián)合任務中生成文本描述，這非常有助于理解模型的行為。此類也可以包括生成用于解釋的符號的方法。此類中的方法在圖像語言聯(lián)合任務（例如從X射線射線照片生成診斷報告）中特別有用。但是，文本解釋不是通用的技術，因為它只有在模型中存在語言模塊時才能起作用。

2.2 事前可解釋的建模

事前可解釋模型可以避免事后可解釋性分析中的偏見。盡管通常認為在可解釋性和模型可表達性之間存在權衡，但仍然有可能找到功能強大且可解釋的模型。一個例子是在[4]中報道的工作，其中可解釋的兩層加性風險模型在FICO識別競賽中獲得了第一名。最近，伯克利馬毅老師基于數(shù)據(jù)壓縮和預測的思想自動構建出一個網(wǎng)絡，是這類方法的一個標志性工作。

可解釋表示（Interpretable Representation）方法采用正則化技術將神經(jīng)網(wǎng)絡的訓練引向更具解釋性的表示。諸如可分解性，稀疏性和單調性之類的屬性可以增強可解釋性。但是，為了可解釋性，損失函數(shù)必須包含正則項，這可能限制了原始模型執(zhí)行其完整的學習任務。

模型修繕（Model Renovation）方法通過將更多可解釋的組件設計和部署來尋求可解釋性。這些組件包括具有專門設計的激活功能的神經(jīng)元，具有特殊功能的插入層，模塊化體系結構等。未來的方向是使用越來越多的可解釋組件，這些組件可以同時為各種任務提供類似的先進性能。

[1] Y. Wang, H. Su, B. Zhang and X. Hu, “Interpret neural networks by identifying critical data routing paths,” In CVPR, 2018.

[2] J. Adebayo, J. Gilmer, M. Muelly, I. Goodfellow, M. Hardt, and B. Kim, “Sanity checks for saliency maps,” In NeurIPS, 2018.

[3] J. L. Kolodner, “An introduction to case-based reasoning,” Artificial intelligence review, vol. 1, no. 6, pp. 3-4, 1992.

[4] C. Chen, K. Lin, C. Rudin, Y. Shaposhnik, S. Wang, T. Wang, “An interpretable model with globally consistent explanations for credit risk,” arXiv preprint, arXiv:1811.12615, 2018.

三.事后可解釋性分析

1. 特征分析

基于invert的方法[1-4]通過將特征圖invert為一個合成的圖像來破解神經(jīng)網(wǎng)絡。例如，A.Mahendran和A. Vedaldi [2] 假設輸入圖像為x_0，對應的神經(jīng)網(wǎng)絡Ω_0的表示為Ω_0=Ω（x_0），其中Ω是神經(jīng)網(wǎng)絡映射，通常不可逆。然后，invert問題被建模成一個優(yōu)化問題：

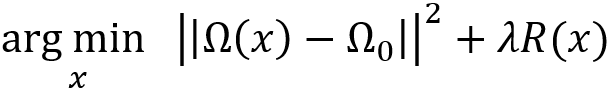
即尋找一個圖像，該圖像的神經(jīng)網(wǎng)絡表示與x_0的神經(jīng)網(wǎng)絡表示最匹配。R（x）是表示有關輸入圖像的先驗知識的正則化項。invert出來圖像之后，我們可以通過比較得到的圖像和原始圖像之間的差異來揭示神經(jīng)網(wǎng)絡丟失的信息。Dosovitskiy [1]直接訓練了一個新網(wǎng)絡，將感興趣模型生成的中間層特征作為輸入，將圖像作為標簽。這樣學到的網(wǎng)絡可以將中間層的特征轉化為圖像。他們發(fā)現(xiàn)即使從很深的層產(chǎn)生的特征中，輪廓和顏色等信息仍然可以重構出來。M.D.Zeiler [4]設計了一個由反卷積+反池化+ReLU操作組成的反向網(wǎng)絡，與原始卷積網(wǎng)絡配對，從而無需訓練就可以直接反轉出特征。在反卷積網(wǎng)絡中，通過標記最大值的位置來實現(xiàn)反池化，反卷積層使用轉置卷積。

激活最大化方法[5-8]致力于合成使神經(jīng)網(wǎng)絡整體或者對某個感興趣的神經(jīng)元的輸出響應最大化的圖像。生成的圖像稱為“deep dream”，因為這些圖像往往比較抽象，具有夢境般的視覺效果。

在[9]，[10]，[11]，[12]，[13]中指出，可以從每個神經(jīng)元中提取有關深度模型的信息。J.Yosinski等[12]直接檢查了不同圖像或視頻的每一層神經(jīng)元的激活值。他們發(fā)現(xiàn)，針對不同輸入而變化的實時神經(jīng)元激活值有助于理解模型的工作方式。Y. Li 等[11]比較了不同初始化生成的特征，以研究神經(jīng)網(wǎng)絡在隨機初始化時是否學習了相似的表示。感受野（Receptive Field, RF）是神經(jīng)元與輸入[14]連接的空間范圍。為了研究神經(jīng)元給定輸入的RF的大小和形狀，B. Zhou等 [13]提出了一種網(wǎng)絡解剖方法，該方法首先為感興趣的神經(jīng)元選擇具有高激活值的K個圖像，然后通過遮擋圖像的局部為每個圖像構建5,000個遮擋圖像，然后將它們輸入到神經(jīng)網(wǎng)絡中，以觀察針對一個神經(jīng)元的激活值的變化。產(chǎn)生較大的差異代表被遮擋的塊兒是重要的。最后，將具有較大差異的遮擋圖像集中并進行平均以生成RF。此外，D. Bau等人 [15]將給定層的低分辨率激活圖放大到與輸入相同的大小，將該圖閾值截斷為二進制激活圖，然后計算二進制激活圖和ground truth二進制分割之間的重疊區(qū)域，作為可解釋性度量。A. Karpathy等 [10]將LSTM 中的門定義為左飽和或右飽和，具體取決于其激活值是小于0.1還是大于0.9。在這方面，經(jīng)常右飽和的神經(jīng)元意味著這些神經(jīng)元可以長時間記住其值。Q.Zhang等 [16]假定較底層中的部件圖案可以來激活下一層中的卷積核。他們逐層挖掘零件圖案，從每一層的特征圖中發(fā)現(xiàn)前一層的部件圖案的激活峰，并構造了一個解釋性的graph來描述層與層特征的關系，其中每個節(jié)點代表一個部件圖案，相鄰層之間的邊代表一個激活關系。

[1] A. Dosovitskiy, T. Brox, “Inverting visual representations with convolutional networks,” In CVPR, pp. 4829-4837, 2016.

[2] A. Mahendran, A. Vedaldi, “Understanding deep image representations by inverting them,” In CVPR, pp. 5188-5196, 2015.

[3] J. T. Springenberg, A. Dosovitskiy, T. Brox and M. Riedmiller, “Striving for simplicity: The all convolutional net,” arXiv preprint, arXiv:1412.6806, 2014.

[4] M. D. Zeiler and R. Fergus, “Visualizing and understanding convolutional networks,” In ECCV, pp. 818-833, 2014.

[5] D. Erhan, Y. Bengio, A. Courville, P. Vincent, “Visualizing higher-layer features of a deep network,” University of Montreal, vol. 1341, no. 3, 2009 Jun 9.

[6] A. Nguyen, A. Dosovitskiy, J. Yosinski, T. Brox & J. Clune, “Synthesizing the preferred inputs for neurons in neural networks via deep generator networks,” In NeurIPS, pp. 3387-3395, 2016.

[7] A. Nguyen, J. Clune, Y. Bengio, A. Dosovitskiy, J. Yosinski, “Plug & play generative networks: Conditional iterative generation of images in latent space,” In CVPR, pp. 4467-4477, 2017.

[8] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, R. Fergus, “Intriguing properties of neural networks,” arXiv preprint, arXiv:1312.6199, 2013.

[9] D. Bau, B. Zhou, A. Khosla, A. Oliva, A. Torralba, “Network dissection: Quantifying interpretability of deep visual representations,” In CVPR, 2017.

[10] A. Karpathy, J. Johnson and L. Fei-Fei, “Visualizing and understanding recurrent networks,” arXiv preprint, arXiv:1506.02078, 2015.

[11] Y. Li, J. Yosinski, J. Clune, H. Lipson, J. E. Hopcroft, “Convergent Learning: Do different neural networks learn the same representations?” In ICLR, 2016.

[12] J. Yosinski, J. Clune, A. Nguyen, T. Fuchs, H. Lipson, “Understanding neural networks through deep visualization,” arXiv preprint, arXiv:1506.06579. 2015.

[13] B. Zhou, A. Khosla, A. Lapedriza, A. Oliva and A. Torralba, “Object detectors emerge in deep scene cnns,” arXiv preprint, arXiv:1412.6856. 2014.

[14] T. Lindeberg, “A computational theory of visual receptive fields,” Biological cybernetics, vol. 107, no. 6, pp. 589-635, 2013.

[15] D. Bau, B. Zhou, A. Khosla, A. Oliva, A. Torralba, “Network dissection: Quantifying interpretability of deep visual representations,” In CVPR, 2017.

[16] Q. Zhang, R. Cao, F. Shi, Y. N. Wu and S. C. Zhu, “Interpreting cnn knowledge via an explanatory graph,” In AAAI, 2018.

2. 模型檢查

P. W. Koh和P. Liang [1]應用影響函數(shù)的概念來解決以下問題：給定一個樣本的預測，數(shù)據(jù)集中的其他樣本對該預測有正面影響還是負面影響？該分析還可以幫助識別數(shù)據(jù)中存在錯誤注釋的標簽和異常值。如圖3所示，給定類似LeNet-5的網(wǎng)絡，通過影響函數(shù)可以識別給定圖像的兩個有害圖像。

圖 3. 根據(jù)影響函數(shù)，兩個對測試圖像有害的樣本在數(shù)據(jù)集中被找到

[2] [3]和 [4]致力于神經(jīng)網(wǎng)絡中故障或偏差的檢測。例如，A.Bansal等人 [2]開發(fā)了一種通用算法，以識別那些神經(jīng)網(wǎng)絡可能無法為其提供任何預測的實例。在這種情況下，該模型將發(fā)出“不要信任我的預測”之類的警告而不是給予一個預測。具體來說，他們使用一系列屬性特征來注釋所有失敗的圖像，并將這些圖像聚類。結果，每個類指示一種故障模式。為了有效地識別那些在數(shù)據(jù)集中具有較高預測分數(shù)的標簽錯誤的實例，H. Lakkaraju等 [3]引入了兩個基本的推測：第一個推測是高可信度地錯誤標記實例是由于系統(tǒng)的偏見而不是隨機擾動，第二個推測則是每個失敗的實例都具有代表性和信息量。然后，他們將圖像分為幾組，并設計搜索策略來搜索失敗實例。為了發(fā)現(xiàn)偏見，Q. Zhang等[4]根據(jù)人類的常識（火對應熱與冰對應冷）利用屬性之間的真實關系來檢查神經(jīng)網(wǎng)絡所挖掘出的屬性關系是否完全符合真實。

Y. Wang等 [5]通過識別關鍵數(shù)據(jù)鏈路理解網(wǎng)絡。具體而言，將門控制二進制矢量λ_k∈{0,1} ^（n_k）與第k層的輸出相乘，其中n_k是第k層中神經(jīng)元的數(shù)量。控制門的開閉則可識別關鍵鏈路，數(shù)學化為搜索λ_1，…，λ_K：

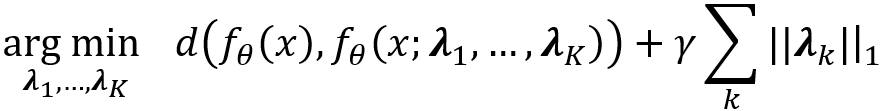
其中f_θ是由用θ參數(shù)化的神經(jīng)網(wǎng)絡表示的映射，f_θ（x; λ_1，...，λ_K）是強制執(zhí)行控制門λ_1，...，λ_K時的映射，d（?，?）是距離度量，γ是一個常數(shù)，控制損失和正則化之間的折衷，||?|| _1是l_1范數(shù)，使得λ_k稀疏。學習的控制門將會暴露模型的重要數(shù)據(jù)處理路徑。B.Kim等 [6]提出了概念激活向量（CAV），它可以定量地測量概念C對網(wǎng)絡任何層的敏感性。首先，訓練二元線性分類器h來區(qū)分兩組樣本刺激的層激活：{f_l（x）：x∈P_C}和{f_l（x）：x?P_C}，其中f_l（x）是在第l層激活層，P_C表示包含概念C的數(shù)據(jù)。然后，將CAV定義為線性分類器超平面的法向單位矢量v_C ^ l，該分類器分類具有和不具有定義概念的樣本。最后，使用v_C ^ l來計算第l層中作為方向導數(shù)的概念C的敏感度：

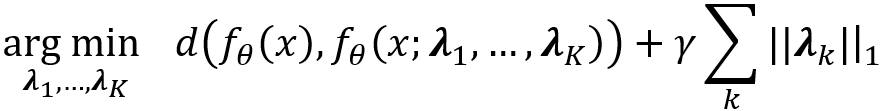
其中h_（l，k）表示針對輸出類別k的訓練后的二分類線性分類器的輸出。J.You等[7]將神經(jīng)網(wǎng)絡映射成關系圖，然后通過大量實驗研究神經(jīng)網(wǎng)絡的圖結構與其預測性能之間的關系（將圖轉錄成網(wǎng)絡并在數(shù)據(jù)集上實現(xiàn)該網(wǎng)絡）。他們發(fā)現(xiàn)網(wǎng)絡的預測性能與兩個圖形度量相關：聚類系數(shù)和平均路徑長度。這項研究的潛力在于，以后進行網(wǎng)絡設計時就無需每種網(wǎng)絡都要跑一次，大大節(jié)省時間，不過這個論文也有缺點，就是他們找到的度量不是單調的，這樣會給使用帶來麻煩。

[1] P. W. Koh and P. Liang, “Understanding black-box predictions via influence functions,” In ICML, 2017.

[2] A. Bansal, A. Farhadi and D. Parikh, “Towards transparent systems: Semantic characterization of failure modes,” In ECCV, 2014.

[3] H. Lakkaraju, E. Kamar, R. Caruana and E. Horvitz, “Identifying unknown unknowns in the open world: Representations and policies for guided exploration,” In AAAI, 2017.

[4] Q. Zhang, W. Wang and S. C. Zhu, “Examining cnn representations with respect to dataset bias,” In AAAI, 2018.

[5] Y. Wang, H. Su, B. Zhang and X. Hu, “Interpret neural networks by identifying critical data routing paths,” In CVPR, 2018.

[6] B. Kim, M. Wattenberg, J. Gilmer, C. Cai, J. Wexler, F. Viegas and R. Sayres, “Interpretability beyond feature attribution: Quantitative testing with concept activation vectors (tcav),” arXiv preprint, arXiv:1711.11279, 2017.

[7] J. You, J. Leskovec, K. He, and S. Xie, “Graph Structure of Neural Networks,” In ICML, 2020.

3. 顯著表征

有很多方法可以獲取顯著性圖。部分依賴圖（Partial Dependence Plot, PDP）和個體條件期望（Individual Conditional Expectation, ICE）[1]，[2]，[3]是使用比較廣泛的統(tǒng)計工具，用于可視化負責任變量和預測變量之間的依賴關系。為了計算PDP，假設有p個輸入維，并且S，C?{1,2，.. p}是兩個互補集，其中S是將要固定的集合，而C是將要改變的集合。然后，通過f_S =∫f（x_S，x_C）dx_C定義x_S的PDP，其中f是模型。與PDP相比，ICE的定義很簡單。通過固定x_C并更改x_S可獲得x_S處的ICE曲線。圖4是一個簡單的示例，分別說明如何計算PDP和ICE。

還有一種簡單的方法也就是各種學科都會用到的控制變量法。即刪除一個特征看模型的變化[4-8]。這個變化是刪除變量產(chǎn)生的，那么自然可以反應這個變量的作用。P.Adler[4]提出應考慮輸入的間接影響。例如，在房屋貸款決策系統(tǒng)中，種族不應成為決策的因素。但是，僅消除種族因素不足以排除種族的影響，因為一些剩余的因素例如“郵政編碼”與種族高度相關（郵編對應居住區(qū)域，黑人區(qū)，白人區(qū)涇渭分明）。

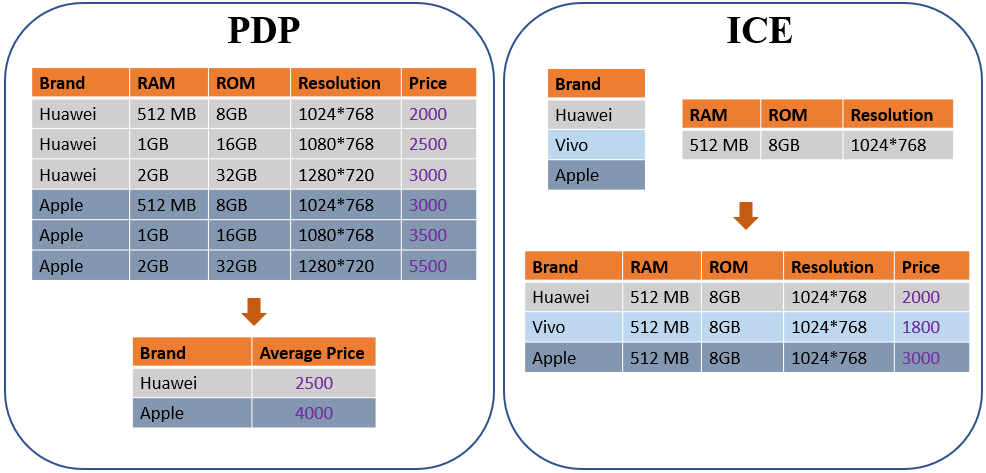
圖 4. 一個簡單的例子解釋PDP 和 ICE. 左邊：為了計算PDP，固定感興趣的變量，讓剩余的變量變化然后求平均。右邊為了計算ICE，讓感興趣的變量直接動

此外，[9-13]中使用了合作博弈的Shapley值。在數(shù)學上，相對于特征i的設定函數(shù)f ?的Shapley值定義為：

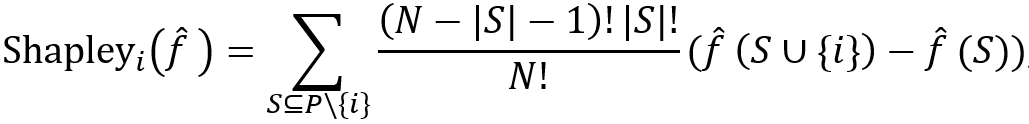
其中|?|是集合的大小，P是N個玩家的總玩家集合，并且集合函數(shù)f ? 將每個子集S?P映射為實數(shù)。可以看出shapley value不止局限于去除一個變量，它運用了其它變量之間的聯(lián)合，因此計算出的變量i的重要性更全面。此外，可以通過用零值替換輸入中不在S中的特征，將Shapley值的定義從一個集合函數(shù)拓展到神經(jīng)網(wǎng)絡函數(shù)f。M. Ancona等人 [6] 為了減少組合爆炸引起的過高的計算成本提出了一種新穎的Shapley值的多項式時間逼近方法，該方法基本上計算了一個隨機聯(lián)合的期望值，而不是枚舉每個聯(lián)合，這樣就降低了shapley value計算的復雜性。圖5顯示了一個簡單示例，說明如何為在一個住房數(shù)據(jù)集上訓練的全連接層網(wǎng)絡計算Shapley值，該網(wǎng)絡包括八個屬性，例如房屋年齡和房間號作為輸入，房屋價格作為標簽。

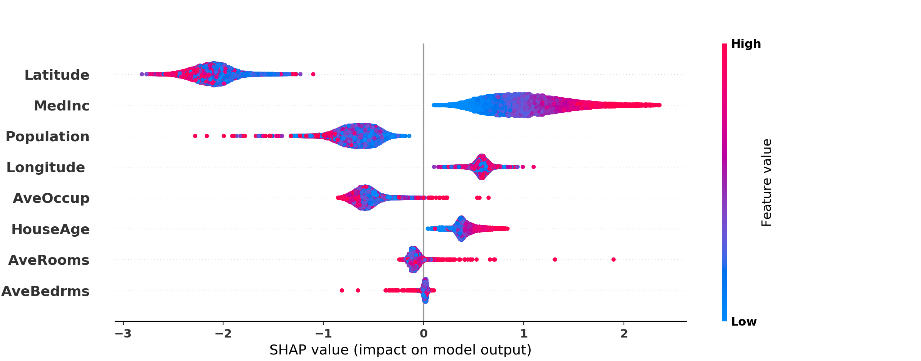
圖5. 正的shapley value值代表正面影響，這里shapley value告訴我們模型可能有異常，因為房屋越老，價格越高，這違反常識

除了直接去除一個或多個特征，借助于梯度也是一個好辦法。K.Simonyan等[14]，D.Smilkov等 [15]，M. Sundararajan等[16]和S. Singla等 [17]利用梯度的思想來探究輸入的顯著性。K.Simonyan等[14]直接計算了類別得分相對于圖像像素的梯度，由此產(chǎn)生了一個類別的顯著性圖。D.Smilkov等 [15]發(fā)現(xiàn)梯度作為顯著度圖噪聲很大。為了消除噪聲，他們提出了“ SmoothGrad”，模型將噪聲多次添加到輸入圖像中，并對得到的梯度圖進行平均：

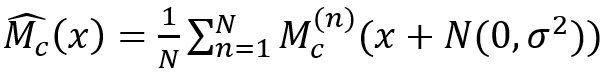
其中M_c^((n))是類別c的梯度圖，N（0，σ^ 2）是具有σ的高斯噪聲作為標準方差。基本上(M_c ) ?(x)是顯著度圖的平滑版本。M. Sundararajan等[16]為顯著性方法設定了兩個基本要求：（敏感度）如果輸入和baseline之間只有一個特征不同，并且輸入和baseline的輸出不同，則該特征應被歸功于顯著性；（實現(xiàn)不變性）在兩個功能上等效的網(wǎng)絡中，同一功能的屬性應相同。M. Sundararajan等注意到較早的基于梯度的顯著性方法未能滿足上述兩個要求，他們提出了積分梯度符合上面兩個條件，公式為：

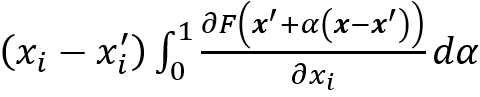
其中F（?）是神經(jīng)網(wǎng)絡映射，x =（x_1，x_2，…，x_N）是輸入，x^'=(x_1^',x_2^',…,x_N^') 是滿足：

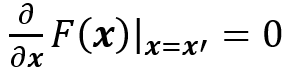
的baseline。實際中，他們將積分轉換為離散求和其中M是逼近積分的步數(shù)。S.Singla等 [17]提出使用泰勒展開式的二階近似來產(chǎn)生顯著性圖。G.Montavon等[20]使用泰勒分解的整個一階項來產(chǎn)生顯著性圖，而不僅僅是梯度。假設 x ? 是模型函數(shù)f(x)事先選好的根f(x ? )=0，因為f（x）可以分解為：

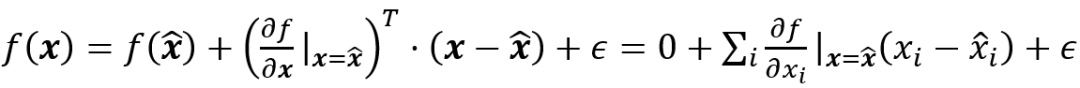
中?為高階項，與像素i相關的像素相關性表示為：

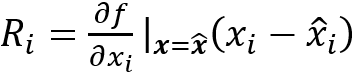
S.Bach等 [18]提出了層級相關性傳播（LRP）。假設模型輸出f（x）在每一層都可以表示為相關性之和。對于輸入層來說，就是輸入圖像的像素級相關性。在最后一層：

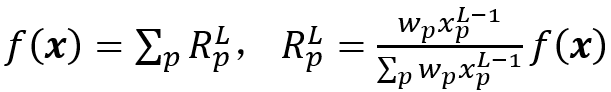
其中L是最后一層，w_p是第（L-1）層的像素p與最終層之間的權重。然后需要定義相關性的傳播關系，給定前饋神經(jīng)網(wǎng)絡，我們定義：

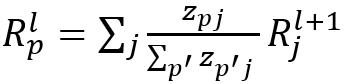
其中

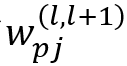
是第l層像素p之間的權重（l + 1）^層的像素j。此外，L. Arras等 [19]將LRP擴展到遞歸神經(jīng)網(wǎng)絡（RNN）以進行情感分析。A. Shrikumar等[21]發(fā)現(xiàn)，即使神經(jīng)元沒有被激活，它仍然有可能揭示有用的信息。因此他們提出了DeepLIFT來計算每個神經(jīng)元的激活與其參考值之間的差異，其中參考值是當網(wǎng)絡被提供參考輸入時該神經(jīng)元的激活，然后將該差異逐層反向傳播到圖像空間。C. Singh等 [22]引入了上下文分解，其層傳播公式為

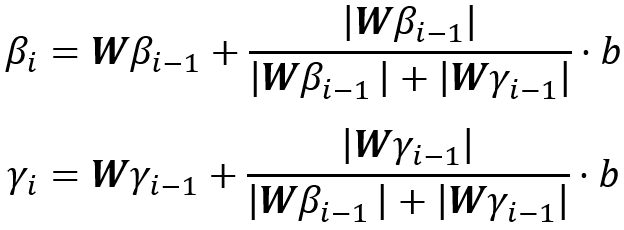
其中W是第i個之間的權重矩陣第i和i-1層，b是偏差向量。β_i（x）被視為輸入的上下文貢獻，而γ_i（x）表示非上下文輸入對g_i（x）的貢獻。僅僅憑借上面兩個公式是沒法解的，還需有限制條件。限制條件是g_i（x）=β_i（x）+γ_i（x），即β_i（x）和γ_i（x）加在一起等于網(wǎng)絡的層的輸出。

圖6.展示了使用類似LeNet-5的網(wǎng)絡對原始梯度，SmoothGrad，IntegratedGrad和Deep Taylor方法的評估。其中，IntegratedGrad和Deep Taylor方法在5位數(shù)字上表現(xiàn)出色

一些其它的方式也可以來得到顯著度圖。比如使用模型的輸入和輸出之間的關聯(lián)的互信息度 [23-25]。此外，T. Lei等 [28]利用生成器來產(chǎn)生能代表原始文本的重要片段，這些片段滿足兩個條件：1）片段應足以替代原始文本；2）片段應簡短而連貫。類似的，求解片段實際上等效于求解一個mask，可以將mask視為顯著性圖。基于以上兩個約束，掩碼的懲罰項可表示為：

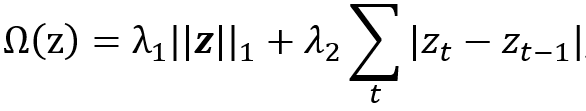
其中z=[z_1,z_2,…]是一個掩碼，第一項控制片段的數(shù)量，第二項控制片段的平滑。

類激活圖（CAM）方法及其變體 [30-31]在全連接層之前使用全局平均池來導出判別區(qū)域。具體來說, 假設 f_k (x,y) 表示第k個特征圖, 給定類別c，那么softmax層的輸入是：

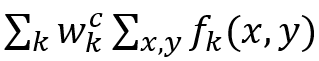
其中 w_k^c 是連接第 k^th 特征圖和類別 c的權重向量。區(qū)分區(qū)域為：

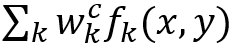
這直接暗示了（x，y）處的像素對于類別c的重要性。此外，還有一些弱監(jiān)督學習方法，例如M. Oquab等[32]也可以得到判別區(qū)域。具體來說，他們只用對象標簽訓練網(wǎng)絡，但是，當他們重新縮放最大池化層生成的特征圖時，令人驚訝地發(fā)現(xiàn)這些特征圖與輸入中對象的位置一致。

[1] J. H. Friedman, “Greedy function approximation: a gradient boosting machine,” Annals of statistics, pp. 1189-232, 2001.

[2] A. Goldstein, A. Kapelner, J. Bleich, E. Pitkin, “Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation,” Journal of Computational and Graphical Statistics, vol. 24, no. 1, pp. 44-65, 2015.

[3] S. Jain, B. C. Wallace, “Attention is not explanation,” arXiv preprint arXiv:1902.10186. 2019.

[4] P. Adler, C. Falk, S. A. Friedler, T. Nix, G. Rybeck, C. Scheidegger, B. Smith, S. Venkatasubramanian, “Auditing black-box models for indirect influence,” Knowledge and Information Systems, vol. 54, no. 1, pp. 95-122, 2018.

[5] A. Kádár, G. Chrupa?a and A. Alishahi, “Representation of linguistic form and function in recurrent neural networks,” Computational Linguistics, vol. 43, no. 4, pp. 761-780, 2017.

[6] J. Li, W. Monroe and D. Jurafsky, “Understanding neural networks through representation erasure,” arXiv preprint, arXiv:1612.08220, 2016.

[7] M. Robnik-?ikonja, I. Kononenko, “Explaining classifications for individual instances,” IEEE Transactions on Knowledge and Data Engineering, vol. 20, no. 5, pp. 589-600, 2008.

[8] L. M. Zintgraf, T. S. Cohen, T. Adel and M. Welling, “Visualizing deep neural network decisions: Prediction difference analysis,” arXiv preprint, arXiv:1702.04595, 2017.

[9] M. Ancona, C. ?ztireli and Gross, “Explaining Deep Neural Networks with a Polynomial Time Algorithm for Shapley Values Approximation,” In ICML, 2019.

[10] G. Casalicchio, C. Molnar and B. Bischl, “Visualizing the feature importance for black box models,” In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pp. 655-670, 2018.

[11] A. Datta, S. Sen, Y. Zick, “Algorithmic transparency via quantitative input influence: Theory and experiments with learning systems,” In IEEE symposium on security and privacy (SP), pp. 598-617, 2016 May.

[12] S. Lipovetsky and M. Conklin, “Analysis of regression in game theory approach,” Applied Stochastic Models in Business and Industry, vol. 17, no. 4, pp. 319-330, 2001.

[13] S. M. Lundberg and S. I. Lee, “A unified approach to interpreting model predictions,” In NeurIPS, 2017.

[14] K. Simonyan, A. Vedaldi and A. Zisserman, “Deep inside convolutional networks: Visualising image classification models and saliency maps,” arXiv preprint, arXiv:1312.6034, 2013.

[15] D. Smilkov, N. Thorat, B. Kim, F. Viégas and M. Wattenberg, “Smoothgrad: removing noise by adding noise,” arXiv preprint, arXiv:1706.03825, 2017.

[16] M. Sundararajan, A. Taly and Q. Yan, “Axiomatic attribution for deep networks,” In ICML, pp. 3319-3328, 2017.

[17] S. Singla, E. Wallace, S. Feng and S. Feizi, “Understanding Impacts of High-Order Loss Approximations and Features in Deep Learning Interpretation,” arXiv preprint, arXiv:1902.00407, 2019.

[18] S. Bach, A. Binder, G. Montavon, F. Klauschen, K. R. Müller & W. Samek, “On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation,” PloS one, vol. 10, no. 7, e0130140, 2015.

[19] L. Arras, G. Montavon, K. R. Müller and W. Samek, “Explaining recurrent neural network predictions in sentiment analysis. arXiv preprint arXiv:1706.07206, 2017.

[20] G. Montavon, S. Lapuschkin, A. Binder, W. Samek, K. R. Müller, “Explaining nonlinear classification decisions with deep taylor decomposition,” Pattern Recognition, vol. 65, pp. 211-22, 2017.

[21] A. Shrikumar, P. Greenside, A. Shcherbina and A. Kundaje, “Not just a black box: Interpretable deep learning by propagating activation differences,” In ICML, 2016.

[22] C. Singh, W. J. Murdoch, B. Yu, “Hierarchical interpretations for neural network predictions,” In ICLR, 2019.

[23] C. Guan, X. Wang, Q. Zhang, R. Chen, D. He, X. Xie, “Towards a Deep and Unified Understanding of Deep Neural Models in NLP,” In ICML, pp. 2454-2463, 2019.

[24] K. Schulz, L. Sixt, F. Tombari, T. Landgraf, “Restricting the flow: Information bottlenecks for attribution,” In ICLR, 2020.

[25] Z. Ying, D. Bourgeois, J. You, M. Zitnik, J. Leskovec, “Gnnexplainer: Generating explanations for graph neural networks,” In Advances in neural information processing systems, pp. 9244-9255, 2019.

[26] A. S. Ross, M. C. Hughes & F. Doshi-Velez, “Right for the right reasons: Training differentiable models by constraining their explanations,” arXiv preprint, arXiv:1703.03717, 2017.

[27] R. C. Fong and A. Vedaldi, “Interpretable explanations of black boxes by meaningful perturbation,” In CVPR, pp. 3429-3437, 2017.

[28] T. Lei, R. Barzilay and T. Jaakkola, “Rationalizing neural predictions,” arXiv preprint, arXiv:1606.04155, 2016.

[30] B. Zhou, A. Khosla, A. Lapedriza, A. Oliva and A. Torralba, “Learning deep features for discriminative localization,” In CVPR, pp. 2921-2929, 2016.

[31] R. R. Selvaraju, M. Cogswell, A. Das, R. Vedantam, D. Parikh & D. Batra, Grad-cam: Visual explanations from deep networks via gradient-based localization. In CVPR, pp. 618-626, 2017.

[32] M. Oquab, L. Bottou, I. Laptev, J. Sivic, “Is object localization for free?-weakly-supervised learning with convolutional neural networks,” In CVPR, pp. 685-694, 2015.

4. 代理模型

代理方法可以分成三類。第一類是直接提取。直接提取的思想是直接從訓練后的模型中構建新的可解釋模型，例如決策樹[1-2]或基于規(guī)則的系統(tǒng)。就提取規(guī)則而言，可以使用decompositional方法[3]和pedagogical方法[4-5]。pedagogical方法提取與神經(jīng)網(wǎng)絡具有相似輸入輸出關系的規(guī)則體系。這些規(guī)則與網(wǎng)絡的權重和結構并不直接對應。例如，有效性間隔分析（VIA）[6]提取以下形式的規(guī)則：

IF（輸入∈某個范圍），THEN輸入屬于某個類。

R. Setiono和H. Liu [3]基于激活值的接近度，對隱藏的單元激活值進行了聚類。然后，每個聚類簇的激活值由它們的平均激活值代替，在此過程中，應選擇合適的聚類類別數(shù)目來盡可能保持神經(jīng)網(wǎng)絡的準確性。接下來，將具有相同平均隱藏單元激活值的輸入數(shù)據(jù)聯(lián)合考慮，這些數(shù)據(jù)的邊界可以幫助我們建立規(guī)則集。在圖7中，我們說明了在Iris數(shù)據(jù)集上使用R. Setiono和H. Liu的方法從一個隱藏層網(wǎng)絡中獲得的規(guī)則。

在用于二分類問題的神經(jīng)網(wǎng)絡中，決策邊界將輸入空間分為兩部分，分別對應于兩個類別。E.W. Saad等人提出HYPINV方法[7]先用片段連續(xù)的決策邊界來計算決策曲線，然后為每個決策邊界超平面片段計算一個切向量。輸入實例與切向量之間的內積符號將暗示輸入實例位于邊界的哪一冊。基于這些內積，我們可以建立一套規(guī)則系統(tǒng)。

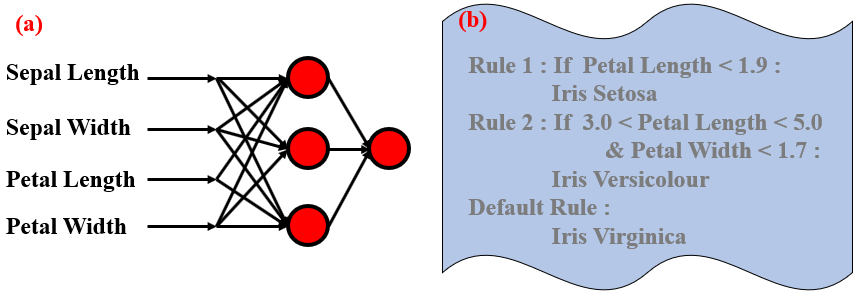
圖 7. 從網(wǎng)絡中提取規(guī)則

最后，一些專門的網(wǎng)絡，例如ANFIS [8]和RBF網(wǎng)絡[9]，直接對應于模糊規(guī)則系統(tǒng)。例如，RBF網(wǎng)絡等效于Takagi-Sugeno規(guī)則系統(tǒng)[10]。論文[11]中將網(wǎng)絡中的每個神經(jīng)元視為一個廣義模糊邏輯門。在這種觀點下，神經(jīng)網(wǎng)絡不過是一個深層的模糊邏輯系統(tǒng)。具體來說，他們分析了一種稱為二次網(wǎng)絡的新型神經(jīng)網(wǎng)絡，其中所有神經(jīng)元都是用二次運算代替內積的二次神經(jīng)元[12]。他們用廣義化的模糊邏輯來解釋二次神經(jīng)元。

第二類方法稱為知識蒸餾[13]，如圖8所示。盡管知識蒸餾技術主要用于模型壓縮，但其原理也可以用于可解釋性。知識蒸餾的核心思想是，復雜的模型可以生成相對準確的預測，將概率分配給所有可能的類別（稱為軟標簽），這些類別可以比one-hot標簽提供更多信息。例如，一匹馬更有可能被歸類為狗而不是山。但是，使用one-hot標簽，狗類和山類的概率都為零。[13]表明原始大模型的泛化能力可以轉移到一個更簡單的模型中。沿著這個方向，我們可以用知識蒸餾的方法開發(fā)可解釋的代理模型，例如決策樹[14-15]，決策集[16]，全局加性模型[17]和更簡單的網(wǎng)絡[18]。例如，S.Tan等[17]使用軟標簽訓練形式為：

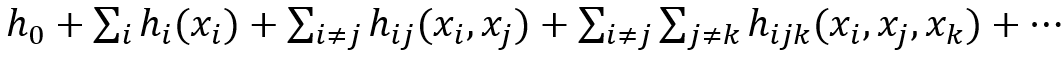
的全局加性模型，其中{h_i }_(i≥1)可直接用作特征顯著性。

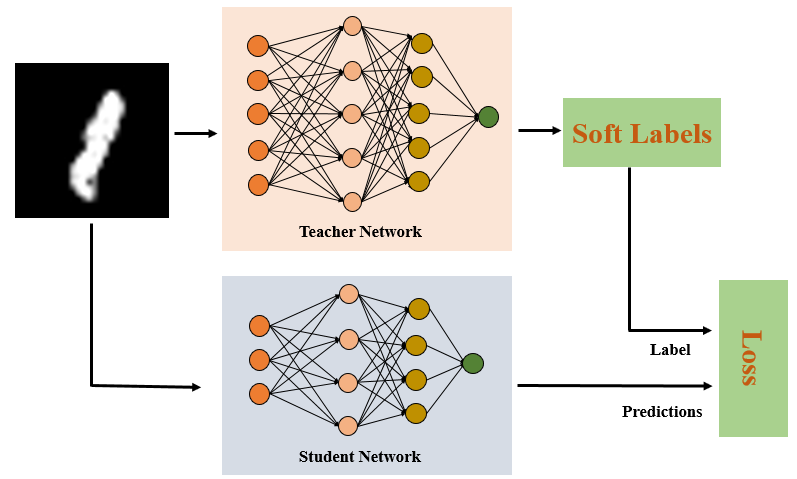
圖 8. 由原始模型產(chǎn)生軟標簽，軟標簽比one-hot標簽更有信息量

最后一類是構造一個local的模型作為代理。local解釋器方法局部地模擬神經(jīng)網(wǎng)絡的預測行為。基本原理是，當從全局來看一個神經(jīng)網(wǎng)絡時，它看起來很復雜。但是如果局部的看一個神經(jīng)網(wǎng)絡的話就會簡單。Local解釋器的代表性方法是LIME[19]，它通過將某些樣本元素隨機設置為零來合成許多鄰居然后計算這些鄰居相應的輸出。最后，使用線性回歸器來擬合這些實例的輸入輸出關系。這個線性回歸器可以在局部模仿神經(jīng)網(wǎng)絡。線性模型的系數(shù)表示特征的貢獻。如圖9所示，LIME方法應用于乳腺癌分類模型，以識別哪些屬性對模型的良性或惡性預測有貢獻。

圖9. 使用LIME來解釋一個乳腺癌分類模型

后續(xù)有方法來改進LIME。Y.Zhang等 [20]指出了LIME解釋中缺乏魯棒性的原因，這源于采樣方差，對參數(shù)選擇的敏感性以及不同數(shù)據(jù)點之間的變化。Anchor[21]是LIME的改進擴展，它可以找到輸入中最重要的部分，那么其余部分的變化就無關緊要，然后就可以只根據(jù)重要部分來生成鄰居。數(shù)學上，Anchor搜索一個集合：A = {z | f（z）= f（x），z∈x}，其中f（?）是模型，x是輸入，z是x的子集。另一項建議是基于[22]的基于局部規(guī)則的解釋（LORE）。LORE利用遺傳算法來平衡的生成鄰居而不是隨機的生成鄰居，從而產(chǎn)生減輕LIME的采樣方差。

[1] R. Krishnan, G. Sivakumar, P. Bhattacharya, “Extracting decision trees from trained neural networks,” Pattern recognition, vol. 1, no. 32, pp. 12, 2019.

[2] C. Yang, A. Rangarajan and S. Ranka, Global model interpretation via recursive partitioning. In IEEE 20th International Conference on High Performance Computing and Communications; IEEE 16th International Conference on Smart City; IEEE 4th International Conference on Data Science and Systems (HPCC/SmartCity/DSS), pp. 1563-1570, 2018, June.

[3] R. Setiono and H. Liu, “Understanding neural networks via rule extraction,” In IJCAI, vol. 1, pp. 480-485, 2017.

[4] E. W. Saad, D. C. Wunsch II, “Neural network explanation using inversion,” Neural networks, vol. 20, no. 1, pp. 78-93, 2007.

[5] S. Thrun, “Extracting rules from artificial neural networks with distributed representations,” In NeurIPS, pp. 505-512, 1995.

[6] F. Maire, “On the convergence of validity interval analysis,” IEEE transactions on neural networks, vol. 11, no. 3, pp. 802-807, 2000.

[7] E. W. Saad, D. C. Wunsch II, “Neural network explanation using inversion,” Neural networks, vol. 20, no. 1, pp. 78-93, 2007.

[8] J. S. Jang, “ANFIS: adaptive-network-based fuzzy inference system,” IEEE transactions on systems, man, and cybernetics, vol. 23, no. 3, pp. 665-685, 1993.

[9] D. Nauck, “A fuzzy perceptron as a generic model for neuro-fuzzy approaches,” Proc. Fuzzy, 1994.

[10] T. Takagi, M. Sugeno, “Fuzzy identification of systems and its applications to modeling and control,” IEEE transactions on systems, man, and cybernetics, pp. 116-32, 1985.

[11] F. Fan and G. Wang, “Fuzzy logic interpretation of quadratic networks,” Neurocomputing, vol. 374, no. 10-21, 2020.

[12] F. Fan and W. Cong and G. Wang, “A new type of neurons for machine learning,” International journal for numerical methods in biomedical engineering, vol. 34, no. 2, e2920, 2018.

[13] C. Buciluǎ, R. Caruana, A. Niculescu-Mizil, “Model compression,” In KDD, pp. 535-541, 2016.

[14] M. W. Craven and J. W. Shavlik, “Extracting Tree-structured Representations of Trained Networks,” In NeurIPS, 1995.

[15] M. Wu, M. C. Hughes, S. Parbhoo, M. Zazzi, V. Roth and F. Doshi-Velez, “Beyond sparsity: Tree regularization of deep models for interpretability,” In AAAI, 2018.

[16] H. Lakkaraju, E. Kamar, R. Caruana, J. Leskovec, “Interpretable & explorable approximations of black box models,” arXiv preprint, arXiv:1707.01154, 2017.

[17] S. Tan, R. Caruana, G. Hooker, P. Koch, A. Gordo, “Learning Global Additive Explanations for Neural Nets Using Model Distillation,” arXiv preprint, arXiv:1801.08640, 2018.

[18] Z. Hu, X. Ma, Z. Liu, E. Hovy and E. Xing, “Harnessing deep neural networks with logic rules,” arXiv preprint, arXiv:1603.06318., 2016.

[19] M. T. Ribeiro, S. Singh, C. Guestrin, “Why should I trust you?: Explaining the predictions of any classifier,” In KDD, pp. 1135-1144, 2016.

[20] Y. Zhang, K. Song, Y. Sun, S. Tan, M. Udell, “Why Should You Trust My Explanation?” Understanding Uncertainty in LIME Explanations,” arXiv preprint, arXiv:1904.12991. 2019.

[21] M. T. Ribeiro, S. Singh, C. Guestrin, “Anchors: High-precision model-agnostic explanations,” In AAAI, 2018.

[22] R. Guidotti, A. Monreale, S. Ruggieri, D. Pedreschi, F. Turini, F. Giannotti, “Local rule-based explanations of black box decision systems,” arXiv preprint, arXiv:1805.10820. 2018.

5. 先進數(shù)理

Y. Lu等[1]表明，許多殘差網(wǎng)絡可以解釋為常微分方程的離散數(shù)值解，即ResNet [2]中殘差塊的內部工作可以建模為u_(n+1)=u_n+f(u_n ), 其中u_n是第n個塊的輸出，而f（u_n）是對于u_n的操作。注意，u_(n+1)=u_n+f(u_n )是常微分方程du/dt=f(u)的單步有限差分近似。[1]這個想法啟發(fā)了ODE-Net [3]的發(fā)明。如圖10所示，通過ODE-Net調整起點和動力學以擬合螺旋。

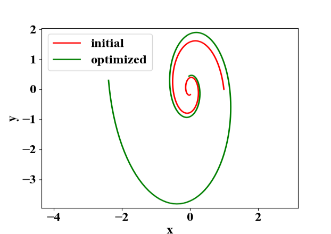
圖 10. ODE-Net 優(yōu)化起點和微分方程去擬合螺旋曲線

N. Lei等[4]在Wasserstein生成對抗網(wǎng)絡（WGAN [5]）和最佳運輸理論之間建立了一種漂亮的聯(lián)系。他們得出結論，在低維假設和特殊設計的距離函數(shù)的情況下，生成器和鑒別器可以精確地用閉式解彼此表示。因此，在WGAN中進行鑒別器和生成器之間的競爭不是必要的。

[6]刻畫了神經(jīng)網(wǎng)絡中間層和網(wǎng)絡輸出之間互信息的大小關系。越深的層與輸出之間互信息越少：

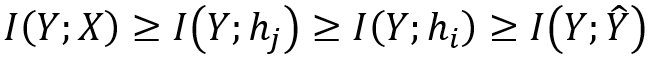
其中I(?;?)表示互信息，h_i,h_j是隱藏層的輸出（i> j表示第i層更深），而Y ?是最終預測。此外，S. Yu和J. C. Principe [7]使用信息瓶頸理論來衡量自編碼器中對稱層的互信息大小關系，如圖11所示。

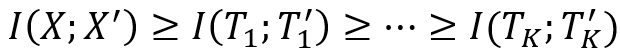
然而，估計互信息比較困難，因為我們通常不知道數(shù)據(jù)的先驗概率分布。

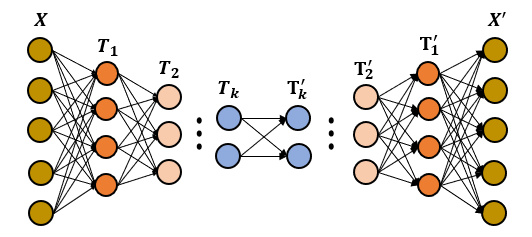
圖 11: 自編碼器對稱層的互信息

S.Kolouri等[8]使用廣義Radon變換建立了神經(jīng)網(wǎng)絡的整體幾何解釋。令X為輸入的隨機變量，其符合分布p_X，則我們可以得出參數(shù)為θ的神經(jīng)網(wǎng)絡f_θ (X)的輸出的概率分布函數(shù)：

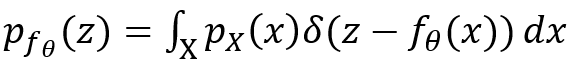
是廣義Radon變換，超曲面為：

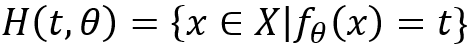
在這個框架下，神經(jīng)網(wǎng)絡的變換的特征在于扭曲超表面重新塑造輸出的概率分布。H. Huang [9]使用平均場理論來描述深度網(wǎng)絡的降維機制，該網(wǎng)絡假定每一層的權重和數(shù)據(jù)服從高斯分布。在他的研究中，將第l層輸出的自協(xié)方差矩陣計算為C^l，然后將固有維數(shù)定義為：

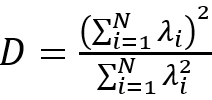
其中λ_i是C^l的特征值，N是特征值的數(shù)目。這樣，我們可以用D / N來分析神經(jīng)網(wǎng)絡中每一層學到的表示是否緊湊。J.C. Ye等 [10]利用低秩Hankel矩陣解釋卷積自編碼器中卷積和廣義池化操作。但是，在他們的研究中，他們簡化了網(wǎng)絡結構，將兩個ReLU單元串聯(lián)為一個線性單元，從而避免ReLU單元的非線性。

理論神經(jīng)網(wǎng)絡研究對于可解釋性也是必不可少的。當前，深度學習的理論基礎主要來自三個方面：表達能力，優(yōu)化和泛化。

表達能力：讓我們在這里舉兩個例子。第一個例子是解釋為什么深層網(wǎng)絡優(yōu)于淺層網(wǎng)絡。受到深層網(wǎng)絡成功的啟發(fā)，L.Szymanski和B. McCane [11]，D.Rolnick和M. Tegmark [12]，N.Cohen等。[13]，H.N. Mhaskar和T. Poggio [14]，R。Eldan和O. Shamir [15]，以及S. Liang和R. Srikant [16]證明深層網(wǎng)絡比淺層網(wǎng)絡更具表現(xiàn)力。基本思想是構造一類特殊的函數(shù)，這些函數(shù)可以有效地由深層網(wǎng)絡來表示，而很難由淺層網(wǎng)絡來近似。第二個示例是了解深度網(wǎng)絡的shortcut連接為什么可以表現(xiàn)好。A. Veit等[17]表明，ResNet的shortcut連接可以使ResNet表現(xiàn)出類似于集成學習的行為。沿著這個方向，[18]證明，有了shortcut連接，窄的神經(jīng)網(wǎng)絡就可以進行通用逼近。

優(yōu)化：深度網(wǎng)絡的優(yōu)化是非凸優(yōu)化問題。我們特別感興趣的是為什么過度參數(shù)化的網(wǎng)絡仍然可以很好地進行優(yōu)化，因為深度網(wǎng)絡是一種過度參數(shù)化的網(wǎng)絡。過度參數(shù)化網(wǎng)絡指的是網(wǎng)絡中的參數(shù)數(shù)量超過了數(shù)據(jù)的數(shù)量。M.Soltanolkotabi等 [21]表明，當數(shù)據(jù)是高斯分布并且神經(jīng)元的激活函數(shù)是二次函數(shù)時，超參數(shù)化的單層網(wǎng)絡允許有效地搜索全局最優(yōu)值。Q. Nguyen和M. Hein [22]證明，對于線性可分離數(shù)據(jù)，在前饋神經(jīng)網(wǎng)絡權重矩陣rank的限制下，損失函數(shù)的每個導數(shù)為零的點都是全局最小值。此外，A.Jacot等人[23]表明，當神經(jīng)網(wǎng)絡的每一層中的神經(jīng)元數(shù)量變得無限大時，訓練只會使網(wǎng)絡函數(shù)發(fā)生很小的變化。結果，網(wǎng)絡的訓練變成了kernel ridge regression。

泛化：傳統(tǒng)的泛化理論無法解釋為何深度網(wǎng)絡有如此多的參數(shù)，仍然可以很好地泛化。最近提出的依賴于權重矩陣范數(shù)的泛化界[24]部分解決了這個問題，即泛化界不是依賴于網(wǎng)絡的參數(shù)個數(shù)而是每一層矩陣的矩陣范數(shù)大小。但是，目前導出的泛化界也有很大問題：比如數(shù)據(jù)越多泛化界越大，這顯然與常識相矛盾。NeurIPS2019年新風向獎也給予了這方面的研究。顯然，我們需要更多的努力才能理解神經(jīng)網(wǎng)絡的泛化難題[25]，[26]。

[1] Y. Lu, A. Zhong, Q. Li, B. Dong, “Beyond finite layer neural networks: Bridging deep architectures and numerical differential equations,” arXiv preprint, arXiv:1710.10121, 2017.

[2] K. He, X. Zhang, S. Ren and Jian Sun, “Deep Residual Learning for Image Recognition”, In CVPR, 2016.

[3] T. Q. Chen, Y. Rubanova, J. Bettencourt & D. K. Duvenaud, Neural ordinary differential equations. In NeurIPS, pp. 6571-6583, 2018.

[4] N. Lei, K. Su, L. Cui, S. T. Yau, X. D. Gu, “A geometric view of optimal transportation and generative model,” Computer Aided Geometric Design, vol. 68, pp. 1-21, 2019.

[5] M. Arjovsky, S. Chintala, L. Bottou, “Wasserstein gan,” arXiv preprint arXiv:1701.07875. 2017.

[6] R. Shwartz-Ziv and N. Tishby, “Opening the black box of deep neural networks via information,” arXiv preprint, arXiv:1703.00810, 2017.

[7] S. Yu and J. C. Principe, “Understanding autoencoders with information theoretic concepts,” Neural Networks, vol. 117, pp. 104-23, 2019.

[8] S. Kolouri, X. Yin, and G. K. Rohde, “Neural Networks, Hypersurfaces, and Radon Transforms,” arXiv preprint, arXiv:1907.02220, 2019.

[9] H. Huang, “Mechanisms of dimensionality reduction and decorrelation in deep neural networks,” Physical Review E, vol. 98, no. 6, pp. 062313, 2018.

[10] J. C. Ye, Y. Han, and E. Cha, “Deep convolutional framelets: A general deep learning framework for inverse problems,” SIAM Journal on Imaging Sciences, vol. 11, no. 2, pp. 991-1048, 2018.

[11] L. Szymanski and B. McCane. Deep networks are effective encoders of periodicity. IEEE transactions on neural networks and learning systems , 25:1816–1827, 2014.

[12] D. Rolnick and M. Tegmark., “The power of deeper networks for expressing natural functions,” In ICLR, 2018.

[13] N. Cohen, O. Sharir, and A. Shashua, “The power of deeper networks for expressing natural functions,” In COLT, 2016.

[14] H. N. Mhaskar and T. Poggio, “Deep vs. shallow networks: An approximation theory perspective,” Analysis and Applications, vol. 14, pp. 829–848, 2016.

[15] R. Eldan and O. Shamir, “The power of depth for feedforward neural networks,” In COLT, 2016.

[16] S. Liang and R. Srikant. Why deep neural networks for function approximation? In ICLR, 2017.

[17] A. Veit, M. J. Wilber, and S. Belongie. Residual networks behave like ensembles of relatively shallow networks. In NeurIPS, 2016.

[18] H. Lin and S. Jegelka, “Resnet with one-neuron hidden layers is a universal approximator,” In NeurIPS, 2018.

[19] R. Ge, F. Huang, C. Jin and Y. Yuan, “Escaping from saddle points—online stochastic gradient for tensor decomposition,” COLT, 2015.

[20] A. Anandkumar and R. Ge, “Efficient approaches for escaping higher order saddle points in non-convex optimization,” In COLT, pp. 81-102, 2016.

[21] M. Soltanolkotabi, A. Javanmard and J. D. Lee, “Theoretical insights into the optimization landscape of over-parameterized shallow neural networks,” IEEE Transactions on Information Theory, vol. 65, no, 2, pp. 742-769, 2018.

[22] Q. Nguyen and M. Hein, “The loss surface of deep and wide neural networks,” In ICML, 2017.

[23] A. Jacot, F. Gabriel, C. Hongler, “Neural tangent kernel: Convergence and generalization in neural networks,” In NeurIPS, pp. 8571-8580, 2018.

[24] B. Neyshabur, R. Tomioka, and N. Srebro. Norm-based capacity control in neural networks.In Conference on Learning Theory, pp. 1376–1401, 2015.

[25] M. Belkin, D. Hsu, S. Ma, S. Mandal, “Reconciling modern machine-learning practice and the classical bias–variance trade-off,” Proceedings of the National Academy of Sciences, vol. 116, no. 32, pp. 15849-54, 2019.

[26] S. Mei, A. Montanari, “The generalization error of random features regression: Precise asymptotics and double descent curve. arXiv preprint, arXiv:1908.05355. 2019.

6. 案例解釋

案例解釋是提供一個案例，該案例被神經(jīng)網(wǎng)絡認為與需要解釋的例子最相似。找到一個相似的案例進行解釋和從數(shù)據(jù)中選擇一個具有代表性的案例作為原型[1]基本上是同一件事，只是使用不同的度量來度量相似性。原型選擇是尋找可以代表整個數(shù)據(jù)集的最小實例子集，案例解釋基于神經(jīng)網(wǎng)絡表示的接近性作為相似性度量，從而可能暴露出神經(jīng)網(wǎng)絡的隱藏表示信息。因此，案例解釋也與深度度量學習有關[2]。

如圖12所示，E.Wallace等[3]采用k近鄰算法來獲取特征空間中查詢案例的最相似案例，然后計算屬于預期類別的最近鄰居的百分比作為可解釋性的度量，表明預測量有多少數(shù)據(jù)支持。C.Chen等[4]構建了一個可以通過發(fā)現(xiàn)原型的一部分來解剖圖像的模型。具體來說，模型的pipeline在卷積層之后分為多個通道，其中每個通道的功能都可以學習輸入的原型部分，例如鳥類的頭部或身體。基于通道所表示的原型部分特征的相似性來確定相似實例。

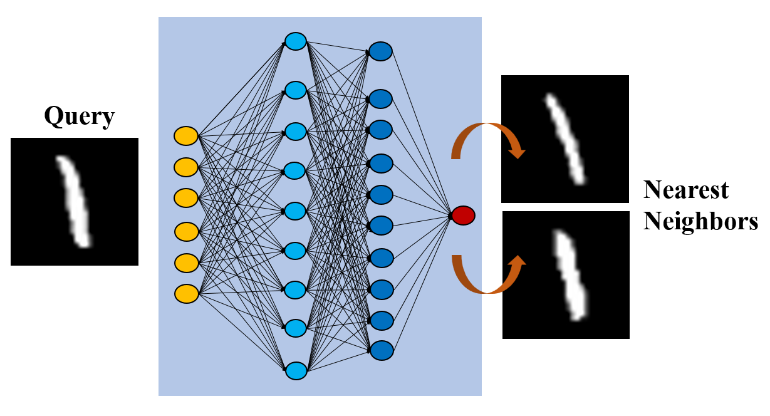
圖 12. 案例解釋提供在神經(jīng)網(wǎng)絡看來與輸入案例最近的鄰居來暴露神經(jīng)網(wǎng)絡的信息

S.Wachter等[5]提供一個反事實案例，這是一種新穎的基于案例的解釋方法。反事實案例是一種假想的案例，它在神經(jīng)網(wǎng)絡的表示中接近查詢案例，但與查詢案例的輸出略有不同。反事實案例解釋提供了所謂的“最可能的另一種情況”或最小的變化以產(chǎn)生不同的結果。例如，反事實的解釋可能會產(chǎn)生以下說法：“如果您有出色的前鋒，您的球隊將贏得這場足球比賽。”巧合的是，產(chǎn)生反事實解釋的技術本質上就是產(chǎn)生“對抗性擾動”[6]。本質上，找到與輸入x最接近的可能情況x'等效于找到對x的最小擾動，從而使分類結果發(fā)生變化。例如，可以構建以下優(yōu)化：

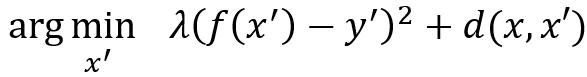
其中λ是一個常數(shù)，y^'是一個不同的標號，并且選擇d（?，?）作為曼哈頓距離，以希望輸入受到的干擾最小。Y. Goyal等 [7]探索了一種替代方法來導出反事實案例。給定帶有標簽c的圖像I，由于反事實的視覺解釋代表輸入的變化，可以迫使模型產(chǎn)生不同的預測類別c'，因此他們選擇了帶有標簽c'的圖像I'，并設法識別出I和I'中的空間區(qū)域，當互換識別區(qū)域時會將模型預測從c更改為c'。

[1] J. Bien, R. Tibshirani, “Prototype selection for interpretable classification,” The Annals of Applied Statistics, vol. 5, no. 4, pp. 2403-24, 2011.

[2] T. Scott, K. Ridgeway, M. C. Mozer, “Adapted deep embeddings: A synthesis of methods for k-shot inductive transfer learning,” In NeurIPS, pp. 76-85, 2018.

[3] E. Wallace, S. Feng, J. Boyd-Graber, “Interpreting Neural Networks with Nearest Neighbors,” arXiv preprint, arXiv:1809.02847, 2018.

[4] C. Chen, O. Li, A. Barnett, J. Su, C. Rudin, “This looks like that: deep learning for interpretable image recognition,” arXiv preprint, arXiv:1806.10574, 2018.

[5] S. Wachter, B. Mittelstadt and C. Russell, “Counterfactual Explanations without Opening the Black Box: Automated Decisions and the GPDR,” Harv. JL & Tech., vol. 31, no. 841, 2017.

[6] K. Xu, S. Liu, G. Zhang, et al., “Interpreting adversarial examples by activation promotion and suppression,” arXiv preprint, arXiv:1904.02057, 2019.

[7] Y. Goyal, Z. Wu, J. Ernst, D. Batra, D. Parikh, and S. Lee, “Counterfactual Visual Explanations,” arXiv preprint, arXiv:1904.07451, 2019.

7. 文本解釋

神經(jīng)圖像字幕使用神經(jīng)網(wǎng)絡為圖像生成自然語言描述。盡管神經(jīng)圖像字幕最初并不是為了網(wǎng)絡的可解釋性，但是有關圖像的描述性語言可以告訴我們神經(jīng)網(wǎng)絡是如何分析圖像的。代表性的方法來自[1]該方法結合了卷積神經(jīng)網(wǎng)絡和雙向遞歸神經(jīng)網(wǎng)絡以獲得雙模態(tài)嵌入。[1]的方法基于這樣的假設：在兩個模態(tài)中表示相似語義的兩個嵌入應該共享兩個空間的附近位置，因此將目標函數(shù)定義為：

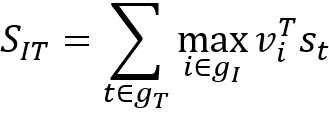
其中v_i是圖像集合g_I中的第i ^個圖像片段，而s_t是句子g_T中的第t個單詞。這樣的模型可以告訴我們網(wǎng)絡的特征對應于什么樣的文本。另一個有代表性的方法是注意力機制[2-5]。文本和注意力圖中的對應詞提供了對深層特征的解釋，反映了圖像的哪些部分吸引了神經(jīng)網(wǎng)絡的注意力。但是S.Jain和BC Wallace [6]認為注意力圖不適合作為解釋，因為他們觀察到注意力圖與基于梯度的熱圖不相關。

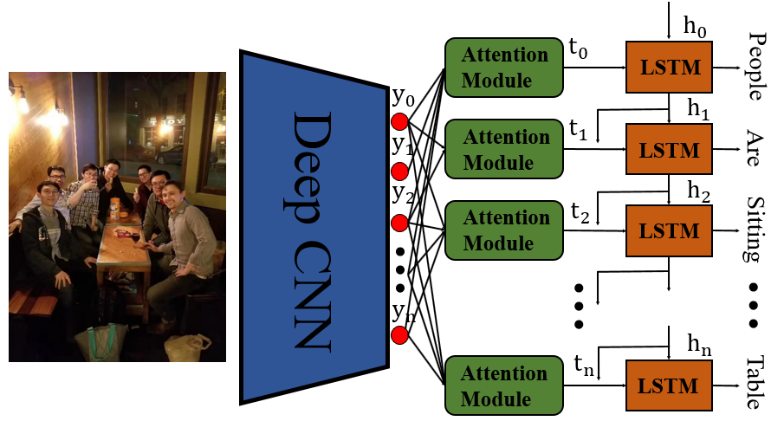
圖 13. 含有注意力機制的圖像標注模塊借助文本提供了網(wǎng)絡的一個解釋

[1] A. Karpathy, L. Fei-Fei, “Deep visual-semantic alignments for generating image descriptions,” In CVPR, pp. 3128-3137, 2015.

[2] B. Patro and V. P. Namboodiri, “Differential attention for visual question answering,” In CVPR, pp. 7680-7688, 2018.

[3] O. Vinyals, A. Toshev, S. Bengio and D. Erhan, “Show and tell: A neural image caption generator,” In CVPR, pp. 3156-3164, 2015.

[4] Q. Xie, X. Ma, Z. Dai and E. Hovy, “An interpretable knowledge transfer model for knowledge base completion,” arXiv preprint, arXiv:1704.05908, 2017.

[5] K. Xu, J. Ba, R. Kiros, K. Cho, A. Courville, R. Salakhudinov, R. Zemel, Y. Bengio, “Show, attend and tell: Neural image caption generation with visual attention,” In ICML, pp. 2048-2057, 2015.

[6] S. Jain, B. C. Wallace, “Attention is not explanation,” arXiv preprint arXiv:1902.10186. 2019.

三.事前可解釋性建模

1. 可解釋表示

傳統(tǒng)上，深度學習的正則化技術主要是為了避免過度擬合而設計的。然而，從分解性[1]，[2]， [3]，單調性[4]，非負性[5]，稀疏性[6], 包括human-in-the-loop的先驗[7] 方面設計正則化技術來增強可解釋的表示也是可行的。

例如，X. Chen等[1]發(fā)明了InfoGAN，它可以促使GAN產(chǎn)生可解釋性的表示。傳統(tǒng)上，生成對抗網(wǎng)絡（GAN）對發(fā)生器如何利用噪聲沒有施加任何限制。而InfoGAN最大化了潛在代碼和觀測值之間的相互信息，從而迫使噪聲的每個維度對語義概念進行編碼，這樣我們就知道每個噪聲維度所代表的意義。特別地，噪聲由離散的分類代碼和連續(xù)的樣式代碼組成。如圖14所示，兩個樣式代碼分別控制數(shù)字的局部部分和數(shù)字旋轉。

圖 14. 在 InfoGAN中，噪聲編碼數(shù)字的局部部分和旋轉部分

納入單調性約束[4]對于增強可解釋性也是有用的。單調關系意味著當指定屬性的值增加時，模型的預測值將單調增加或減少，這種簡單的關系促進了可解釋性。J. Chorowski和J. M. Zurada [5]對神經(jīng)網(wǎng)絡的權重施加非負性，并認為它可以改善可解釋性，因為它消除了神經(jīng)元之間的抵消和混疊效應。A. Subramanian等[6]采用k稀疏自動編碼器進行詞嵌入，以提高嵌入的稀疏性，并也聲稱這樣可以增強可解釋性是因為稀疏嵌入減少了詞之間的重疊。Lage等 [7]提出了一種新穎的human-in-the-loop的正則化。具體來說，他們訓練了多種模型并將其發(fā)送給用戶進行評估。要求用戶預測某個模型將為數(shù)據(jù)點分配什么標簽。響應時間越短，表示用戶對模型的理解就越好。然后，選擇響應時間最短的模型。

[1] X. Chen, Y. Duan, R. Houthooft, J. Schulman, I. Sutskever, and P. Abbeel, “Infogan: Interpretable representation learning by information maximizing generative adversarial nets,” In NeurIPS, 2016.

[2] A. Stone, H. Wang, M. Stark, Y. Liu, D. S. Phoenix and D. George, “Teaching compositionality to cnns,” In CVPR, pp. 5058-5067, 2017.

[3] Q. Zhang, Y. N. Wu and S. C. Zhu, “Interpretable convolutional neural networks,” In CVPR, pp. 8827-8836, 2018.

[4] S. You, D. Ding, K. Canini, J. Pfeifer and M. Gupta, “Deep lattice networks and partial monotonic functions,” In NeurIPS, pp. 2981-2989, 2017.

[5] J. Chorowski and J. M. Zurada, “Learning understandable neural networks with nonnegative weight constraints,” IEEE transactions on neural networks and learning systems, vol. 26, no. 1, pp. 62-69, 2014.

[6] A. Subramanian, D. Pruthi, J. H. Jhamtani, T. Berg-Kirkpatrick and E. Hovy, “Spine: Sparse interpretable neural embeddings,” In AAAI, 2018.

[7] I. Lage, A. Ross, S. J. Gershman, B. Kim, and F. Doshi-Velez, “Human-in-the-loop interpretability prior,” In NeurIPS, pp. 10159-10168, 2018.

2. 模型修繕

L.Chu等 [1]提出使用分段線性函數(shù)作為神經(jīng)網(wǎng)絡（PLNN）的激活函數(shù)（也包括ReLU），PLNN有十分明確的決策邊界，并且我們可以導出封閉形式的解來求解網(wǎng)絡的決策邊界。如圖15所示，F(xiàn).Fan等[2] 提出了軟自動編碼器（Soft-AE），軟自編碼器在編碼層中使用自適應的軟閾值單元和在解碼層中使用線性單元。因此，軟自編碼器可以解釋為一個可學習的級聯(lián)小波自適應系統(tǒng)。

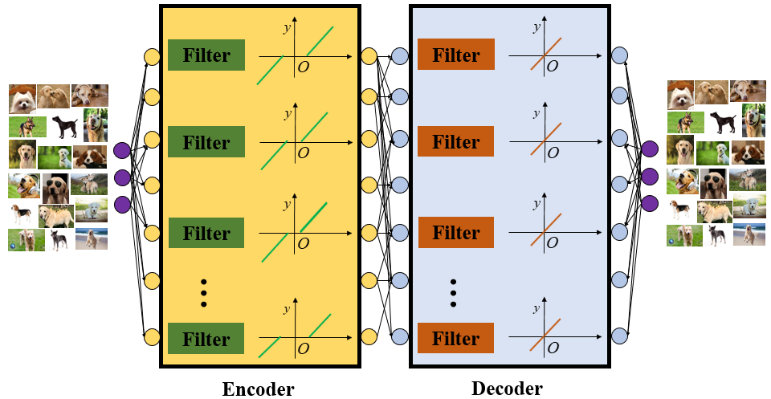
圖 15.軟自編碼器在編碼層中使用自適應的軟閾值單元和在解碼層中使用線性單元。因此，軟自編碼器可以解釋為一個可學習的級聯(lián)小波自適應系統(tǒng)

L. Fan [3]通過修改偏差項將神經(jīng)網(wǎng)絡解釋為廣義漢明（Hamming）網(wǎng)絡，其神經(jīng)元計算廣義漢明距離：

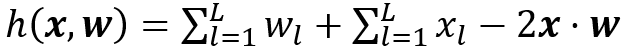
這里輸入是x=(x_1,…,x_L)和權重向量w=(w_1,…,w_L). 如果我們將每個神經(jīng)元中的偏差項指定為：

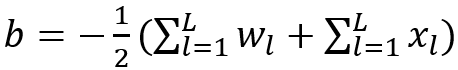
每個神經(jīng)元是廣義漢明神經(jīng)元。在這種觀點下，batch-normalization的功能就可以解釋了：batch-normalization就是為了讓偏差來配湊出廣義漢明距離。C.C.J.Kuo等人[4]提出了一種透明的設計，用于構造前饋卷積網(wǎng)絡，而無需反向傳播。具體來說，通過為早期池化層的輸出選擇PCA的主成分來構建卷積層中的濾波器。然后用線性平方回歸器來構建全連接層。

DA Melis和T. Jaakkola [5]認為，如果神經(jīng)網(wǎng)絡模型f具有以下形式，則它是可解釋的：

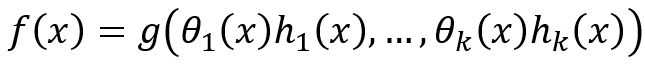
其中h_i（x）是輸入x的原型特征，而θ_i（x）是與該概念相關的重要性，g是單調的并且完全可加分離。這樣的模型可以學習可解釋的基礎概念并且方便進行顯著性分析。類似地，J.Vaughan等[6]設計了一種網(wǎng)絡結構，這種結構對應的輸出函數(shù)是：

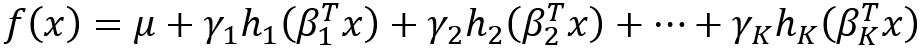
的函數(shù)，其中β_k是投影，h_k（?）表示非線性變換，μ是偏差，而γ_k是加權因子。這樣的模型比一般的網(wǎng)絡更具解釋性，因為該模型的功能具有更簡單的偏導數(shù)，可以簡化顯著性分析，統(tǒng)計分析等。

C. Li等[7]提出了通過在中間層的特征上使用層級標簽，比如“人→中國人→安徽人”來進行深度監(jiān)督。具體來說，我們有一個數(shù)據(jù)集{（x，y_1，…，y_m）}，其中標簽y_1，…，y_m是分層的。我們使用分層標簽去監(jiān)督深度網(wǎng)絡的層，然后網(wǎng)絡里的層就會依次學到對應的標簽的特征。然后我們可以從top-level上感知到層的功能。這種方案引入了模塊化的思想，從而獲得可解釋性。

T. Wang [8]建議對那些只要簡單模型就可以分類的數(shù)據(jù)使用可解釋和可插入的替代模型。在他們的工作中，將規(guī)則集構建為可解釋的模型，以便首先對輸入數(shù)據(jù)進行分類。那些規(guī)則集難以分類的輸入將傳遞到黑盒模型中進行決策。這種混合預測系統(tǒng)的邏輯是，在不影響準確性的情況下，可以為常規(guī)案件提供可解釋的模型，為復雜案件提供復雜的黑匣子模型。

C. Jiang等[9]提出了有限自動機遞歸神經(jīng)網(wǎng)絡（FA-RNN），可以將其FA-RNN直接轉換為正則表達式，從而獲得解釋力。具體來說，可以將構造的FA-RNN近似為有限自動機，然后將其轉換為正則表達式，因為有限自動機和正則表達式可以相互轉換。以此類推，正則表達式也可以解碼為FA-RNN作為初始化。FA-RNN是體現(xiàn)規(guī)則系統(tǒng)和神經(jīng)網(wǎng)絡之間協(xié)同作用的一個很好的例子。

[1] L. Chu, X. Hu, J. Hu, L. Wang and J. Pei, “Exact and consistent interpretation for piecewise linear neural networks: A closed form solution,” In KDD, pp. 1244-1253, 2018, July.

[2] F. Fan, M. Li, Y. Teng and G. Wang, “Soft Autoencoder and Its Wavelet Adaptation Interpretation,” IEEE Transactions on Computational Imaging, vol. 6, pp. 1245-1257, 2020.

[3] L. Fan, “Revisit fuzzy neural network: Demystifying batch normalization and ReLU with generalized hamming network,” In NeurIPS, pp. 1923-1932, 2017.

[4] C. C. C. J. Kuo, M. Zhang, S. Li, J. Duan and Y. Chen, “Interpretable convolutional neural networks via feedforward design,” Journal of Visual Communication and Image Representation, vol. 60, pp. 346-359, 2019.

[5] D. A. Melis and T. Jaakkola, “Towards robust interpretability with self-explaining neural networks,” In NeurIPS, pp. 7775-7784, 2018.

[6] J. Vaughan, A. Sudjianto, E. Brahimi, J. Chen, and V. N. Nair, “Explainable neural networks based on additive index models,” arXiv preprint, arXiv:1806.01933, 2018.

[7] C. Li, et al., “Deep supervision with intermediate concepts,” IEEE transactions on pattern analysis and machine intelligence, vol. 41, no. 8, 1828-1843, 2018.

[8] T. Wang, “Gaining Free or Low-Cost Interpretability with Interpretable Partial Substitute,” In ICML, pp. 6505-6514, 2019.

[9] C. Jiang, Y. Zhao, S. Chu, L. Shen, and K. Tu, "Cold-start and Interpretability: Turning Regular Expressions into Trainable Recurrent Neural Networks". In EMNLP, 2020.

四.深入討論

1. 深度學習與規(guī)則系統(tǒng)

模糊邏輯[1]在上個世紀九十年代中非常火。它將布爾邏輯從0-1判斷擴展到可以取[0，1]中的任何值的推斷。模糊理論可以分為兩個分支：模糊集理論和模糊邏輯理論。后者以“ IF-THEN”規(guī)則為重點，并以IF-THEN規(guī)則的形式表示一個系統(tǒng)，在處理大量復雜的系統(tǒng)建模和控制問題方面顯示出了有效性。然而，基于模糊規(guī)則的系統(tǒng)也受到很大限制，構建模糊規(guī)則的過程繁瑣且計算量大。神經(jīng)網(wǎng)絡是一種數(shù)據(jù)驅動的方法，它通過訓練從數(shù)據(jù)中提取知識，但是神經(jīng)網(wǎng)絡所表示的知識是分布在每個神經(jīng)元中的。在數(shù)據(jù)量較小的情況下，神經(jīng)網(wǎng)絡無法提供令人滿意的結果，并且缺乏可解釋性。神經(jīng)網(wǎng)絡和模糊邏輯系統(tǒng)是互補的。因此，將兩個世界的優(yōu)點結合起來對于增強可解釋性有幫助。實際上，這個路線圖并不是全新的。沿著這個方向有幾種可能的模型：ANFIS模型[2]，通用模糊感知器[3]，RBF網(wǎng)絡[4]等。

我們可以建立一個深層的RBF網(wǎng)絡。給定輸入向量x = [x_1，x_2，…，x_n]，RBF網(wǎng)絡表示為：

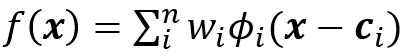
其中?_i（x-c_i）為通常選擇為：

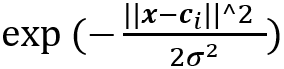
其中c_i是第i個神經(jīng)元的簇中心。[4]證明了在溫和條件下RBF網(wǎng)絡與模糊推理系統(tǒng)之間的功能等效性。同樣，RBF網(wǎng)絡可以作為通用逼近器[5]。因此，RBF網(wǎng)絡是一種潛在的可靠的載體，自帶規(guī)則而不會損失準確性。而且與多層感知器相比，自適應RBF網(wǎng)絡中的規(guī)則生成和模糊規(guī)則表示更為簡單。盡管當前的RBF網(wǎng)絡只是具有一層隱藏的結構，但開發(fā)深層的RBF網(wǎng)絡是可行的，可以將深層RBF視為深層的模糊規(guī)則系統(tǒng)。貪婪訓練算法[6]成功地解決了深度網(wǎng)絡的訓練問題。可以將這種成功應用在深度RBF網(wǎng)絡的訓練。然后，使用深度RBF網(wǎng)絡與深度模糊邏輯系統(tǒng)之間的對應關系來獲得深度模糊規(guī)則系統(tǒng)。

[1] L. A. Zadeh, “Fuzzy logic,” Computer, vol. 21, no. 4, pp. 83-93, 1988.

[2] J. S. Jang, “ANFIS: adaptive-network-based fuzzy inference system,” IEEE transactions on systems, man, and cybernetics, vol. 23, no. 3, pp. 665-685, 1993.

[3] D. Nauck, “A fuzzy perceptron as a generic model for neuro-fuzzy approaches,” Proc. Fuzzy, 1994.

[4] C. Bishop, “Improving the generalization properties of radial basis function neural networks,” Neural computation, vol. 3, no. 4, pp. 579-88, 1991.

[5] J. Park and I. W. Sandberg, “Universal approximation using radial-basis-function networks,” Neural computation, vol. 3, no. 2, 246-257, 1991.

[6] G. E. Hinton, S. Osindero, Y. W. The, “A fast learning algorithm for deep belief nets,” Neural computation, vol. 18, no. 7, pp. 1527-54, 2006.

2. 深度學習與腦科學

迄今為止，真正的復雜智能系統(tǒng)仍然只有人類大腦。早期形式的人工神經(jīng)網(wǎng)絡顯然受到了生物神經(jīng)網(wǎng)絡的啟發(fā)[1]。然而，神經(jīng)網(wǎng)絡的后續(xù)發(fā)展卻基本不是由神經(jīng)科學的觀點來推動的。就可解釋性而言，由于生物和人工神經(jīng)網(wǎng)絡之間有著深厚的聯(lián)系，神經(jīng)科學的進步與深度學習技術的發(fā)展和解釋有密切的關系。我們認為，神經(jīng)科學在以下幾個方面將為深度學習解釋性帶來廣闊的前景。

損失函數(shù)：有效的損失函數(shù)是過去幾年中深度網(wǎng)絡發(fā)展的重要動力；例如，GAN中使用的對抗性損失[2]。在之前的技術部分中，我們重點介紹了一些損失函數(shù)的案例，這些案例表明適當?shù)膿p失函數(shù)將使模型能夠學習可解釋的表示形式，例如增強特征可分離性。我們的大腦是一個最好的優(yōu)化機器[3]，該機器具有強大而準去的權重分配機制。通過研究大腦，可以幫助我們建立生物學上合理的損失函數(shù)。

優(yōu)化算法：盡管反向傳播取得了巨大的成功，但從神經(jīng)科學的角度來看，它遠非理想。實際上，從許多方面講，反向傳播都無法表現(xiàn)出人類神經(jīng)系統(tǒng)調節(jié)神經(jīng)元突觸的真實方式。例如，在生物神經(jīng)系統(tǒng)中，突觸以局部方式更新[4]，并且僅取決于突觸前和突觸后神經(jīng)元的活動。但是，深度網(wǎng)絡中的連接是通過非本地反向傳播進行調整的。另外，與人腦的內部工作相比，深度網(wǎng)絡中缺少類似神經(jīng)調節(jié)劑的機制：其中一個神經(jīng)元的狀態(tài)可以表現(xiàn)出受全局神經(jīng)調節(jié)劑（如多巴胺，5-羥色胺等）控制的不同輸入輸出模式[5] 。人們認為神經(jīng)調節(jié)劑至關重要，因為它們能夠選擇性地控制一種神經(jīng)元的開和關狀態(tài)，從而等效地對神經(jīng)元實現(xiàn)了模塊化的控制 [6]。考慮到現(xiàn)在很少有研究討論訓練算法的可解釋性，因此我們非常需要功能強大且可解釋的訓練算法。

生物合理的結構設計：在過去的幾十年中，神經(jīng)網(wǎng)絡架構發(fā)展從簡單的前饋網(wǎng)絡到深度卷積網(wǎng)絡以及其他高度復雜的網(wǎng)絡。我們知道結構確定功能，即，特定的網(wǎng)絡體系結構調節(jié)具有不同特征的信息流。當前，深度學習和生物大腦系統(tǒng)之間的結構差異非常明顯。神經(jīng)網(wǎng)絡基于大數(shù)據(jù)來完成大多數(shù)任務，而生物大腦系統(tǒng)可以從少量數(shù)據(jù)中學習并得到很好的概括。我們需要借鑒生物神經(jīng)網(wǎng)絡，以便可以設計出更理想，更可解釋的神經(jīng)網(wǎng)絡結構。相關的研究已經(jīng)出現(xiàn)，比如MIT的研究者使用線蟲的神經(jīng)系統(tǒng)（僅有幾十個神經(jīng)元）構建了一個小型自動駕駛控制器 [7]。

[1] W. S. McCulloch and W. Pitts, “A logical calculus of the ideas immanent in nervous activity,” The bulletin of mathematical biophysics, vol. 5, no. 4, pp. 115-133, 1943.

[2] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, “Generative adversarial nets,” In NeurIPS, pp. 2672-2680, 2014.

[3] A. H. Marblestone, G. Wayne and K. P. Kording, “Toward an integration of deep learning and neuroscience,” Frontiers in computational neuroscience, vol. 10, no. 94, 2016.

[4] D. Krotov and J. J. Hopfield, “Unsupervised learning by competing hidden units,” Proceedings of the National Academy of Sciences, vol. 116, no. 16, pp. 7723-7731, 2019.

[5] S. H. Snyder, “Adenosine as a neuromodulator,” Annual review of neuroscience, vol. 8, no. 1, pp. 103-24, 1985.

[6] C. I. Bargmann, “Beyond the connectome: how neuromodulators shape neural circuits,” Bioessays, vol. 34, no. 6, pp. 458-65, 2012.

[7] M. Lechner, R. Hasani, A. Amini, T. A. Henzinger, D. Rus, R. Grosu, “Neural circuit policies enabling auditable autonomy,” Nature Machine Intelligence, vol. 2, no. 10, pp. 642-52, 2020.


個人微信（如果沒有備注不拉群！）
請注明：地區(qū)+學校/企業(yè)+研究方向+昵稱



下載1：何愷明頂會分享

在「AI算法與圖像處理」公眾號后臺回復：何愷明，即可下載。總共有6份PDF，涉及 ResNet、Mask RCNN等經(jīng)典工作的總結分析

下載2：終身受益的編程指南：Google編程風格指南

在「AI算法與圖像處理」公眾號后臺回復：c++，即可下載。歷經(jīng)十年考驗，最權威的編程規(guī)范！


下載3 CVPR2021

在「AI算法與圖像處理」公眾號后臺回復：CVPR，即可下載1467篇CVPR 2020論文 和 CVPR 2021 最新論文
點亮 ，告訴大家你也在看

深度學習可解釋性兩萬字綜述