3D數(shù)學(xué)基礎(chǔ)(二)| 向量
前言3D數(shù)學(xué)基礎(chǔ)：圖形與游戲開發(fā)
這是白玉無冰記錄3D數(shù)學(xué)第二篇章，向量！往期目錄如下：
在寫之前，白玉無冰一直在思考如何去講述向量，思來想去，還是以實際問題例子出發(fā)，去講這個神奇的向量！
本文不打算講過多的定義和推導(dǎo)，更多地以例子出發(fā)去探討。如果需要更深入地理解，可參考文末給出的參考書籍與資料。
開始基本定義
向量(vector)描述了方向和大小。向量也有自己的運(yùn)算規(guī)則，向量的加減法與數(shù)乘的意義見下圖。
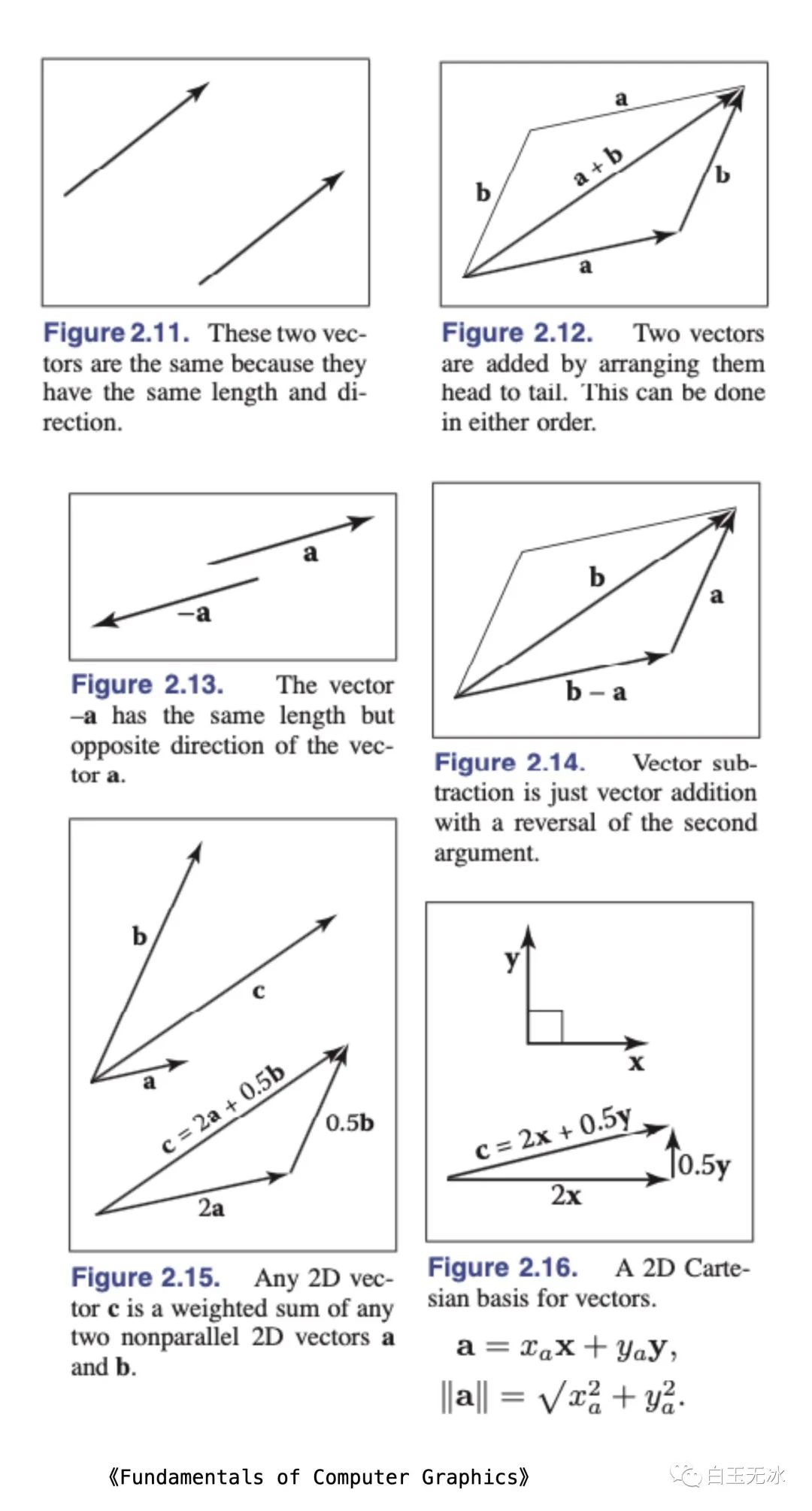向量加法與數(shù)乘除了向量間的加法，向量之間還存在著兩種乘法：
- 點乘(Dot Product)
- 叉乘(Cross Product)
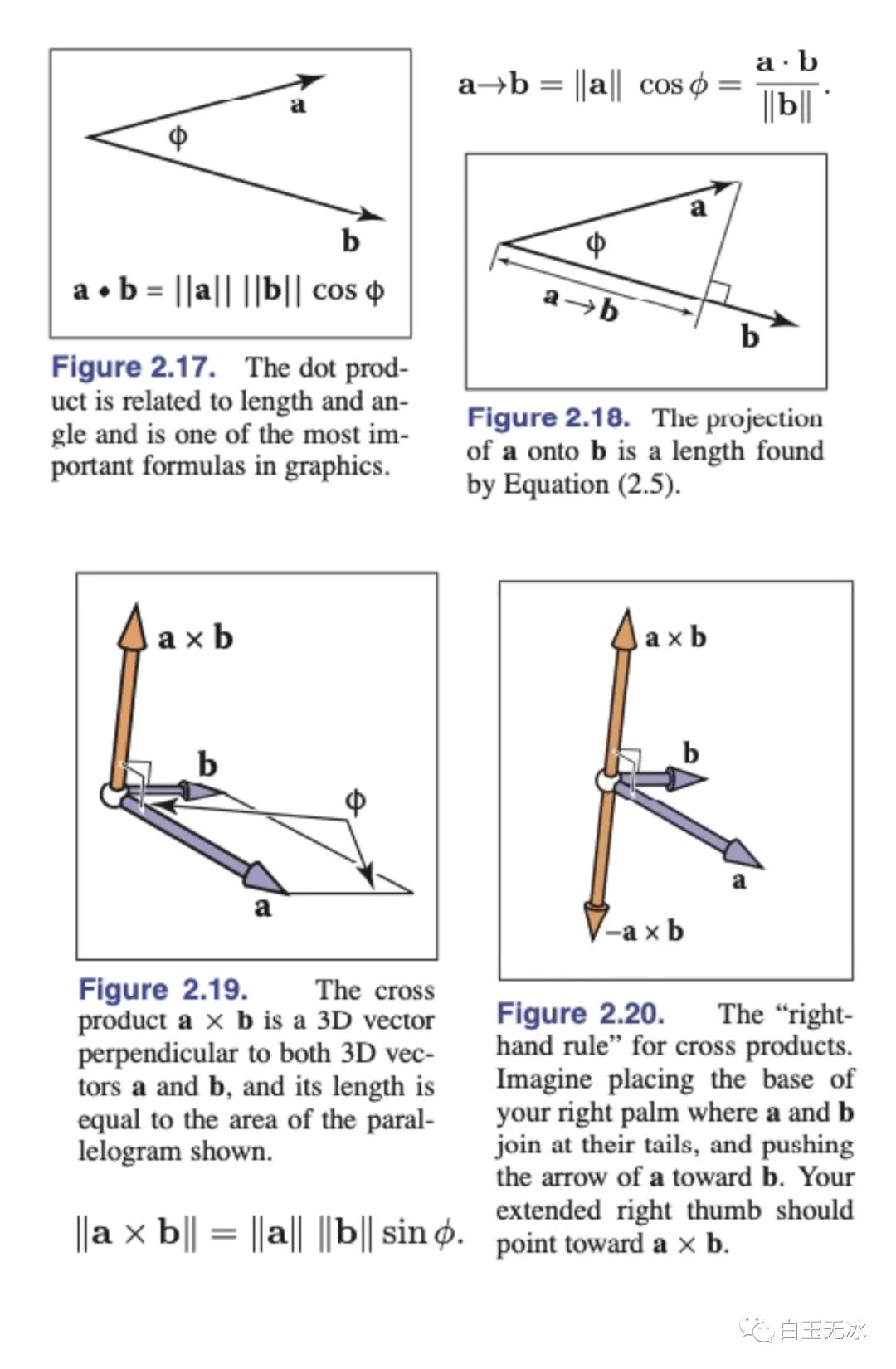向量點乘與叉乘向量反射
已知：
- 入射向量
- 單位法線量
- 入射角與反射角相同
求:
- 反射向量
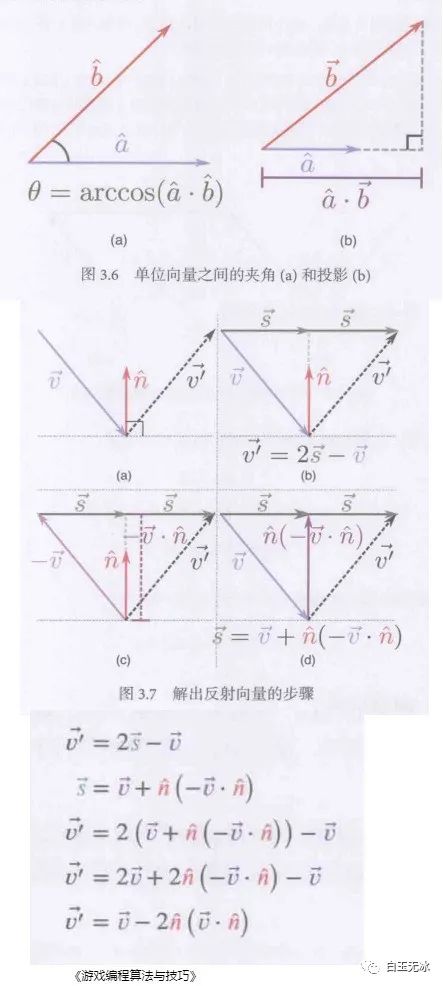向量反射在反復(fù)橫跳的瞄準(zhǔn)線這篇文章也用到了反射向量的計算。
反復(fù)橫跳的瞄準(zhǔn)線旋轉(zhuǎn)2D角色
已知：
- 角色位置和朝向
- 目標(biāo)位置
求:
- 角色往哪個方向旋轉(zhuǎn)多少度可朝向目標(biāo)位置
旋轉(zhuǎn)2D角色概況來說，求角度用點乘，求旋轉(zhuǎn)方向用叉乘。
旋轉(zhuǎn)2D角色求解在 Cocos Creator 中的 Vec2 使用 signAngle 的邏輯也是如此。
//?class?Vec2
/**
*?@en?Get?angle?in?radian?between?this?and?vector?with?direction.
*?@zh 獲取當(dāng)前向量和指定向量之間的有符號角度。
*?有符號角度的取值范圍為?(-180, 180]，當(dāng)前向量可以通過逆時針旋轉(zhuǎn)有符號角度與指定向量同向。
*?@param?other?specified?vector
*?@return?The?signed?angle?between?the?current?vector?and?the?specified?vector?(in?radians);?if?there?is?a?zero?vector?in?the?current?vector?and?the?specified?vector,?0?is?returned.
*/
public?signAngle?(other:?Vec2)?{
????const?angle?=?this.angle(other);
????return?this.cross(other)?0???-angle?:?angle;
}
判斷多邊形凹凸點
已知：
- 多邊形的頂點坐標(biāo)（逆時針，簡易多邊形）
求：
- 判斷每個點的凹凸性
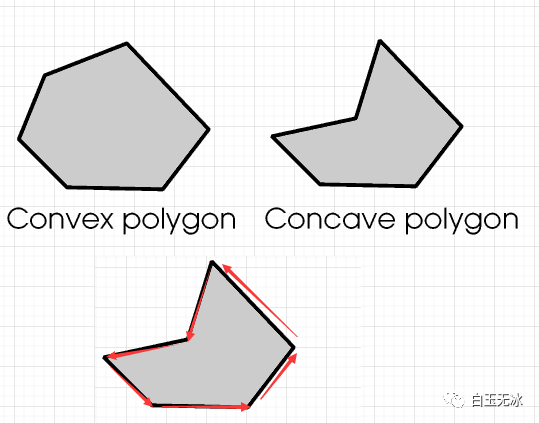凹凸多邊形巧用向量叉乘即可求解。
在多邊形裁剪圖片中的切耳法用到了這個判斷。
判斷三角形內(nèi)的點
已知：
- 三角形三個點
- 其中一個共面的點
求：
- 該點是否在三角形內(nèi)
判斷點是否在三角形內(nèi)，可以通過叉乘計算點與線的位置關(guān)系判斷出。
點是否在三角形內(nèi)在 GAMES 103-02 中提到，也可用法向量判斷。
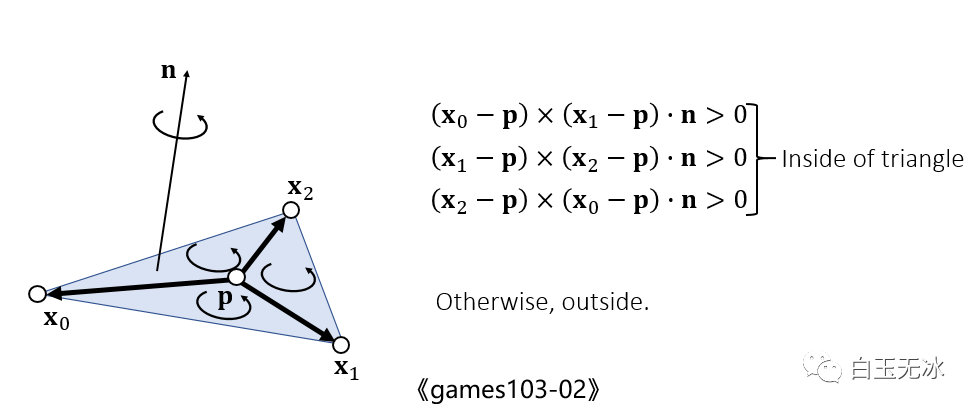點是否在三角形內(nèi)前后左右
已知：
- 各個飛機(jī)的坐標(biāo)和黑色飛機(jī)的朝向。
求：
- 其他飛機(jī)與黑色飛機(jī)前后左右的關(guān)系？
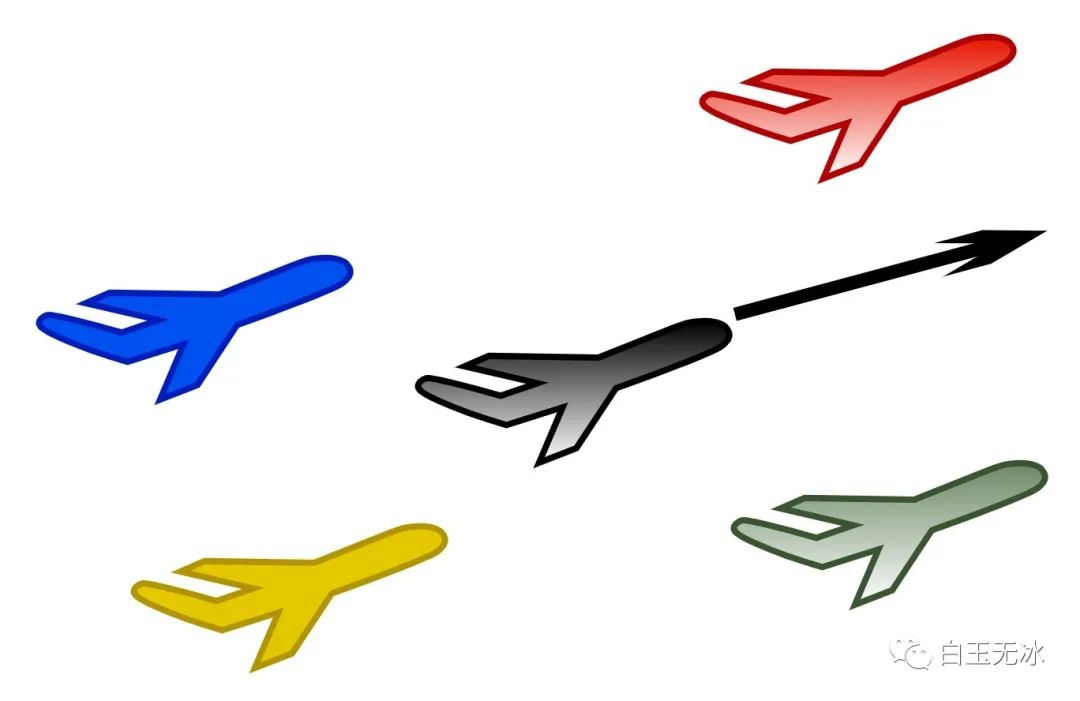前后左右解答：
- 點乘 -> 前后
- 叉乘 -> 左右
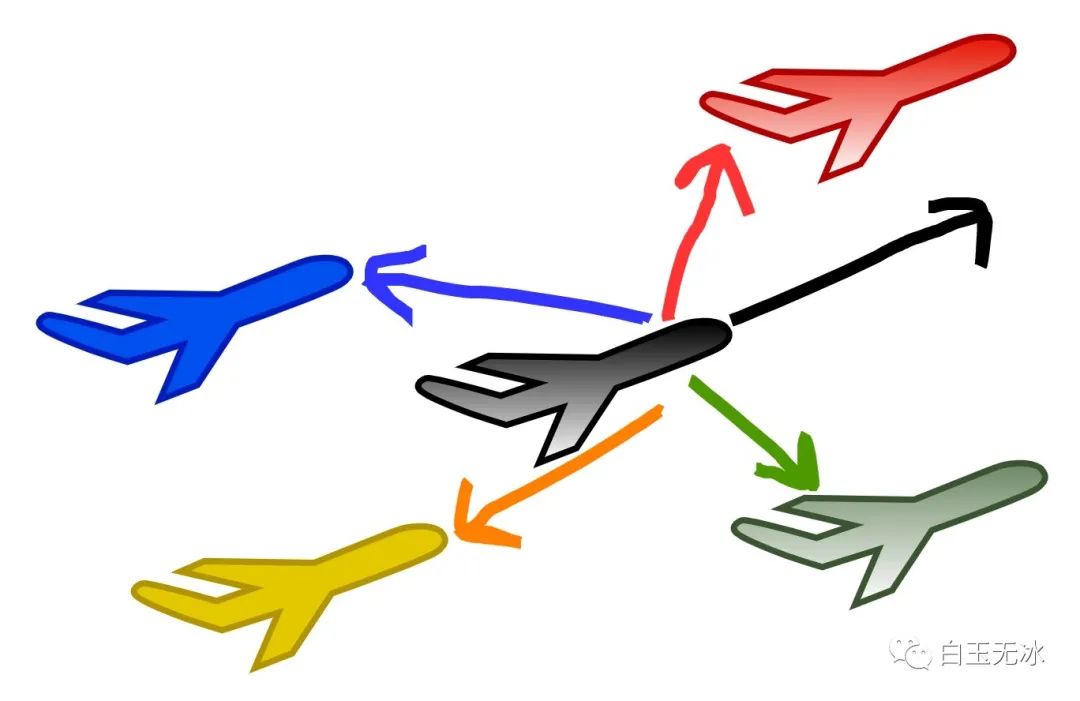前后左右折紙效果
在【折紙效果！(2D)】中也涉及一些向量計算，這里搬運(yùn)過來，詳細(xì)講解可點擊文章鏈接查看。
折紙效果分割多邊形的點。向量間的點積正好可以幫助我們判斷夾角問題。
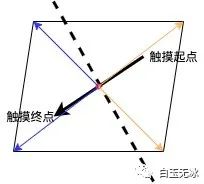
分割求對稱點同樣可以運(yùn)用向量計算。
- 求出該頂點與中點的向量
- 求出該點在觸摸方向的單位向量的投影(點乘)，這正好是距離的一半
- 求出對稱點坐標(biāo)（距離乘方向向量+起始點坐標(biāo)）
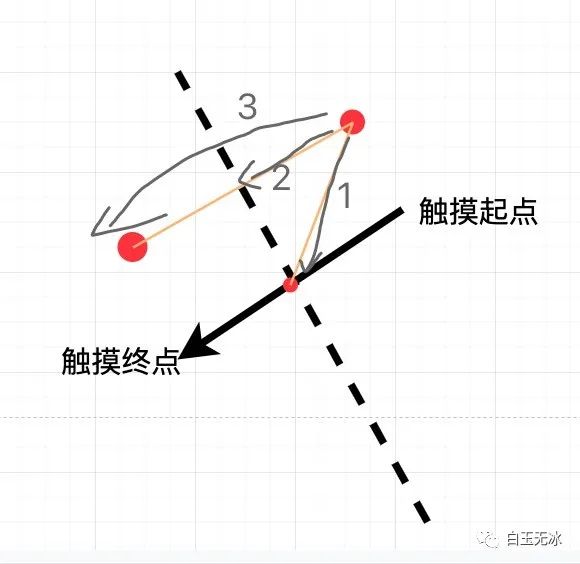求對稱點在【3D折紙效果】同樣也使用到向量相關(guān)的知識。
效果預(yù)覽使用向量叉乘判斷網(wǎng)格點在觸摸軸的左邊還是右邊。
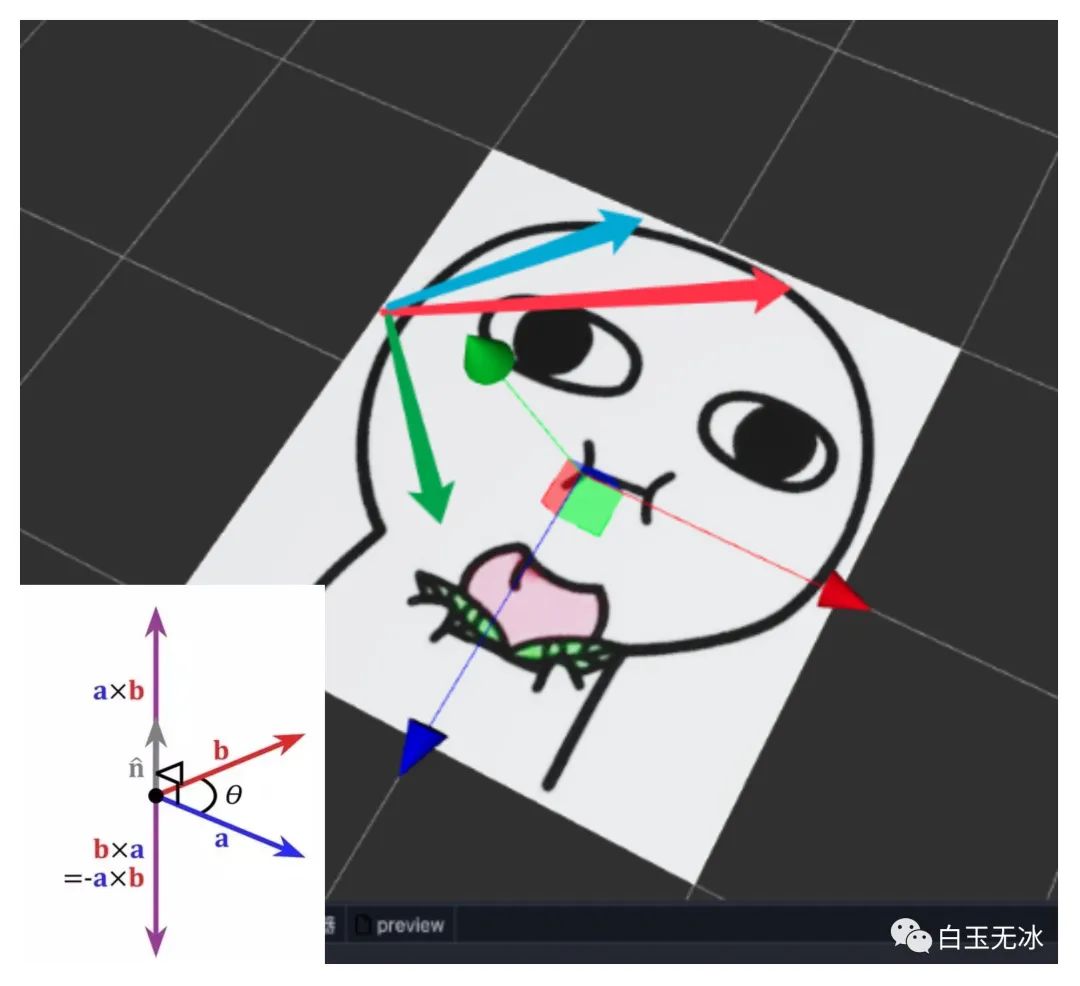向量叉乘矢量和平面
本段摘自《游戲編程精粹2》中的2.2章節(jié)。
已知：
- 起點 終點
- 平面單位法線向量 和面上的一個點
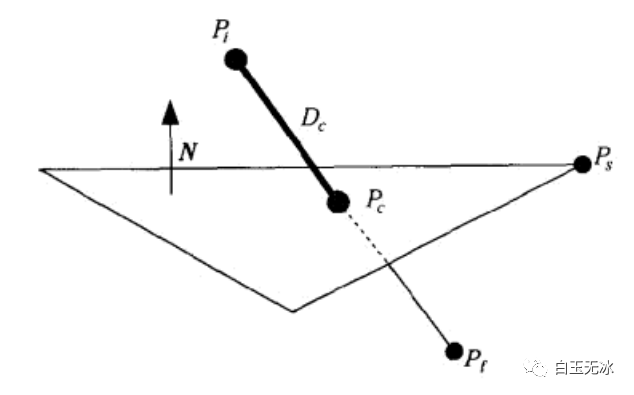矢量和平面求：相對于面的高度（點乘）
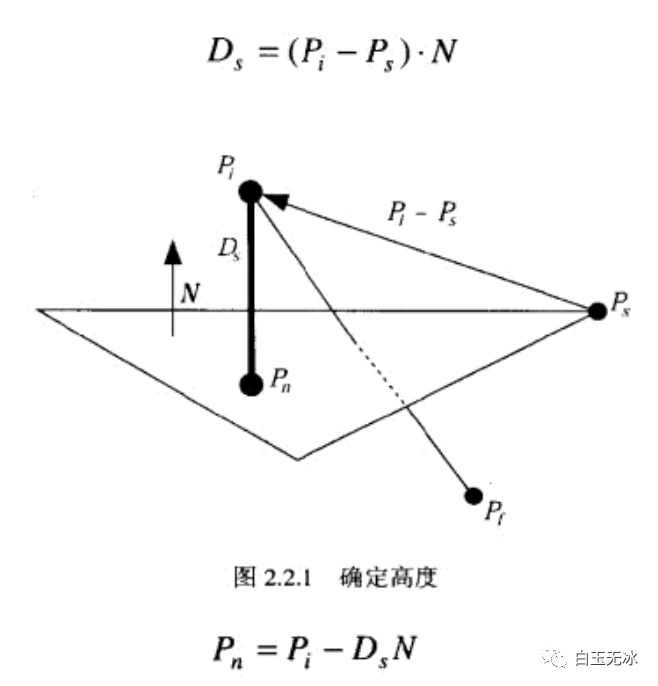相對于面的高度求：直接與平面相交點（投影到法向量，相似三角形）
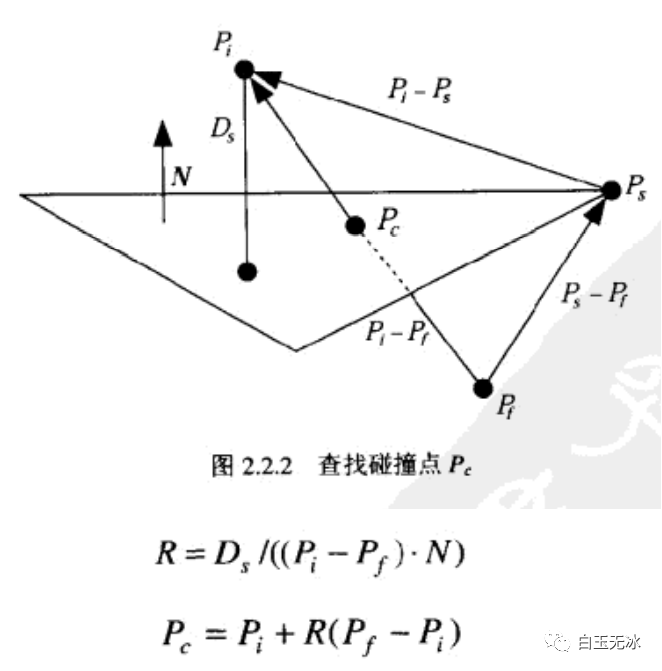直接與平面相交點求：到交點的距離（兩種方法）
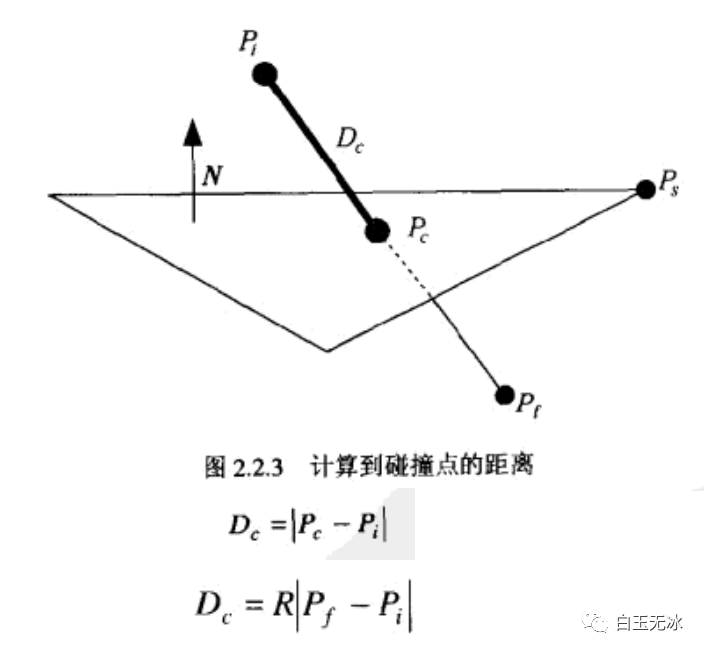到交點的距離計算反射點
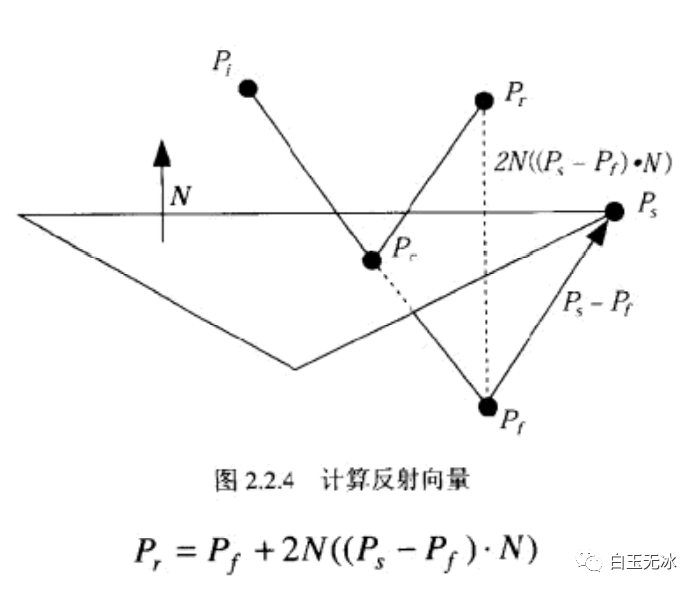計算反射點向量空間
本部分內(nèi)容摘自《3D游戲與計算機(jī)圖形學(xué)中的數(shù)學(xué)方法》1.4節(jié)，記錄是為了更好的忘記。
向量空間向量的基
向量的基加上相互垂直條件，正交基
正交基再加上單位長度限制，正交規(guī)范基。
正交規(guī)范基自然數(shù)
講到向量，這里再扯點其他和向量相關(guān)的。
自然數(shù)也可以分解成正交基向量表示。互質(zhì)的自然數(shù)，正好與向量垂直對應(yīng)。
自然數(shù)分解結(jié)束預(yù)期白玉無冰下一篇記錄關(guān)于矩陣的筆記??。
參考資料
- 《3D數(shù)學(xué)基礎(chǔ)：圖形與游戲開發(fā)》
- 《Fundamentals of Computer Graphics, Fourth Edition》
- 《游戲編程算法與技巧》
- http://games-cn.org/
- 《游戲編程精粹2》
- 《3D游戲與計算機(jī)圖形學(xué)中的數(shù)學(xué)方法》
- 《數(shù)學(xué)女孩2》
更多精彩歡迎關(guān)注微信公眾號
往期系列：