實際工程項目中是怎么用卡爾曼濾波的?
點擊下方卡片,關(guān)注“新機器視覺”公眾號
重磅干貨,第一時間送達
計算機視覺life整理
原文鏈接:https://www.zhihu.com/question/358334095
就比如飛行器姿態(tài)估計,導航定位,目標跟蹤,圖像處理等的實際項目中,是如何先把問題抽象成數(shù)學模型,然后再一步步解決的?最后又封裝成產(chǎn)品
作者:李崇
兩大難題,一是運動學模型的建立,也就是預測方程。這個一方面可以通過比較細的系統(tǒng)辨識來做,這方面要結(jié)合具體的應用背景,不一而足,也是普遍做的比較差的地方。
另一方面可用某個傳感器的輸出來做預測,比較典型的就是用加速度計做預測,再用陀螺做更新。
另一大問題就是噪聲的統(tǒng)計特性咯。因為建模誤差不知道。觀測方程到還可以測一下ZRO算一下均值和方差。然后下一步就是大家喜聞樂見的調(diào)參的階段咯,據(jù)說是群魔亂舞花樣百出。
我現(xiàn)實中只用過mems加速度計和陀螺的融合,還有就是無模型的跟蹤咯。也就是預測方程是0,純靠建模誤差的那個方差來做預測,效果咋說呢,穩(wěn)態(tài)下看噪聲統(tǒng)計特性是好了些,但是動態(tài)特性明顯滯后和變形了。應該是我經(jīng)驗不足吧
作者:雁集
先啰嗦一下在工程中卡爾曼濾波要解決的問題是什么。
我們得到了2(或多個)個反饋同一件事的信息A和B,但不知道該相信哪個結(jié)果,所以簡單的,將兩個信息相加除以2(加權(quán)平均),得到一個結(jié)果0.5A+0.5B。但這個方法過于粗暴,不能反映出水平。現(xiàn)在知道了其中一個信息可靠度更好,而另一個可靠度不好,就要更相信好的信息,如,現(xiàn)在給可信度好的B更大的權(quán)重,得到0.2A+0.8B,這個結(jié)果會好于第一個。但仍然覺得low,因為A與B的參數(shù)是根據(jù)經(jīng)驗設(shè)置的,并不知道是否是最合理的,是否是最優(yōu)化的。所以高級的,用優(yōu)化的方法,根據(jù)A與B的高斯分布特征,去融合A和B信息,這個就是卡爾曼。
所以,我們看到,要利用卡爾曼,需要不同的信息源(大于等于2個)。最常見的信息源是什么?就是我們根據(jù)系統(tǒng)模型或動力學模型計算出來的結(jié)果,可以通過仿真的形式得到。第二個或第三個信息是什么?在飛行器姿態(tài)估計,導航定位,目標跟蹤(幾個問題的本質(zhì)一樣,都是狀態(tài)估計)的問題中,這個信息一般來自慣導或GPS或雷達等。有了2個信息數(shù)據(jù),就可以根據(jù)Kalman的公式進行融合。下面舉一個機器人運動估計的例子,來自《Probabilistic Robotics》。
首先假設(shè)你的機器人長這樣(一個圓,比較簡單),在二維笛卡爾坐標系中運動。

根據(jù)這個圖,可以得到它的運動學模型
經(jīng)典的速度、角速度、角度模型,飛行器、輪式機器人、AUV都可以這樣簡單描述
得到以上模型還不能直接用,這個模型有變量的乘積和三角函數(shù),是個非線性模型,但要利用卡爾曼公式,需要滿足EKF(實際工程應用中,我還沒見過直接用KF的)的線性化條件。所以要將非線性的模型線性化。

到這一步,得到的Gt可以直接代入EKF公式去更新協(xié)方差矩陣了,經(jīng)過推算會得到增益矩陣K。EKF公式包括預測與更新,這里就不啰嗦了。
同時,用狀態(tài)的迭代形式,可以得到初步推算的位置
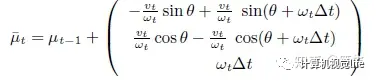
最后,EKF公式中有一項
(z是最終的觀測值,最簡單的,觀測矩陣可以是單位陣,反應的是全狀態(tài))
其中兩個z,代表了2個信息,比如其中一個是通過動力學得到的機器人位置,另一個通過雷達得到的機器人位置。
通過以上的計算,會得到一個靠譜的結(jié)果。
Kalman的其它公式都是用優(yōu)化理論去解算高斯函數(shù)的,在此不啰嗦了。
聲明:部分內(nèi)容來源于網(wǎng)絡(luò),僅供讀者學習、交流之目的。文章版權(quán)歸原作者所有。如有不妥,請聯(lián)系刪除。
