PCA的數(shù)學(xué)原理

數(shù)學(xué)算法俱樂(lè)部

日期 ： 2021年07月08日       

正文共 ：7172字

來(lái)源 ： 網(wǎng)絡(luò)

PCA（Principal Component Analysis）是一種常用的數(shù)據(jù)分析方法。PCA通過(guò)線性變換將原始數(shù)據(jù)變換為一組各維度線性無(wú)關(guān)的表示，可用于提取數(shù)據(jù)的主要特征分量，常用于高維數(shù)據(jù)的降維。網(wǎng)上關(guān)于PCA的文章有很多，但是大多數(shù)只描述了PCA的分析過(guò)程，而沒(méi)有講述其中的原理。這篇文章的目的是介紹PCA的基本數(shù)學(xué)原理，幫助讀者了解PCA的工作機(jī)制是什么。

當(dāng)然我并不打算把文章寫(xiě)成純數(shù)學(xué)文章，而是希望用直觀和易懂的方式敘述PCA的數(shù)學(xué)原理，所以整個(gè)文章不會(huì)引入嚴(yán)格的數(shù)學(xué)推導(dǎo)。希望讀者在看完這篇文章后能更好的明白PCA的工作原理。

數(shù)據(jù)的向量表示及降維問(wèn)題

一般情況下，在數(shù)據(jù)挖掘和機(jī)器學(xué)習(xí)中，數(shù)據(jù)被表示為向量。例如某個(gè)淘寶店2012年全年的流量及交易情況可以看成一組記錄的集合，其中每一天的數(shù)據(jù)是一條記錄，格式如下：

(日期, 瀏覽量, 訪客數(shù), 下單數(shù), 成交數(shù), 成交金額)

其中“日期”是一個(gè)記錄標(biāo)志而非度量值，而數(shù)據(jù)挖掘關(guān)心的大多是度量值，因此如果我們忽略日期這個(gè)字段后，我們得到一組記錄，每條記錄可以被表示為一個(gè)五維向量，其中一條看起來(lái)大約是這個(gè)樣子：

注意這里我用了轉(zhuǎn)置，因?yàn)榱?xí)慣上使用列向量表示一條記錄（后面會(huì)看到原因），本文后面也會(huì)遵循這個(gè)準(zhǔn)則。不過(guò)為了方便有時(shí)我會(huì)省略轉(zhuǎn)置符號(hào)，但我們說(shuō)到向量默認(rèn)都是指列向量。

我們當(dāng)然可以對(duì)這一組五維向量進(jìn)行分析和挖掘，不過(guò)我們知道，很多機(jī)器學(xué)習(xí)算法的復(fù)雜度和數(shù)據(jù)的維數(shù)有著密切關(guān)系，甚至與維數(shù)呈指數(shù)級(jí)關(guān)聯(lián)。當(dāng)然，這里區(qū)區(qū)五維的數(shù)據(jù)，也許還無(wú)所謂，但是實(shí)際機(jī)器學(xué)習(xí)中處理成千上萬(wàn)甚至幾十萬(wàn)維的情況也并不罕見(jiàn)，在這種情況下，機(jī)器學(xué)習(xí)的資源消耗是不可接受的，因此我們必須對(duì)數(shù)據(jù)進(jìn)行降維。

降維當(dāng)然意味著信息的丟失，不過(guò)鑒于實(shí)際數(shù)據(jù)本身常常存在的相關(guān)性，我們可以想辦法在降維的同時(shí)將信息的損失盡量降低。

舉個(gè)例子，假如某學(xué)籍?dāng)?shù)據(jù)有兩列M和F，其中M列的取值是如何此學(xué)生為男性取值1，為女性取值0；而F列是學(xué)生為女性取值1，男性取值0。此時(shí)如果我們統(tǒng)計(jì)全部學(xué)籍?dāng)?shù)據(jù)，會(huì)發(fā)現(xiàn)對(duì)于任何一條記錄來(lái)說(shuō)，當(dāng)M為1時(shí)F必定為0，反之當(dāng)M為0時(shí)F必定為1。在這種情況下，我們將M或F去掉實(shí)際上沒(méi)有任何信息的損失，因?yàn)橹灰Ａ粢涣芯涂梢酝耆€原另一列。

當(dāng)然上面是一個(gè)極端的情況，在現(xiàn)實(shí)中也許不會(huì)出現(xiàn)，不過(guò)類(lèi)似的情況還是很常見(jiàn)的。例如上面淘寶店鋪的數(shù)據(jù)，從經(jīng)驗(yàn)我們可以知道，“瀏覽量”和“訪客數(shù)”往往具有較強(qiáng)的相關(guān)關(guān)系，而“下單數(shù)”和“成交數(shù)”也具有較強(qiáng)的相關(guān)關(guān)系。這里我們非正式的使用“相關(guān)關(guān)系”這個(gè)詞，可以直觀理解為“當(dāng)某一天這個(gè)店鋪的瀏覽量較高（或較低）時(shí)，我們應(yīng)該很大程度上認(rèn)為這天的訪客數(shù)也較高（或較低）”。后面的章節(jié)中我們會(huì)給出相關(guān)性的嚴(yán)格數(shù)學(xué)定義。

這種情況表明，如果我們刪除瀏覽量或訪客數(shù)其中一個(gè)指標(biāo)，我們應(yīng)該期待并不會(huì)丟失太多信息。因此我們可以刪除一個(gè)，以降低機(jī)器學(xué)習(xí)算法的復(fù)雜度。

上面給出的是降維的樸素思想描述，可以有助于直觀理解降維的動(dòng)機(jī)和可行性，但并不具有操作指導(dǎo)意義。例如，我們到底刪除哪一列損失的信息才最小？亦或根本不是單純刪除幾列，而是通過(guò)某些變換將原始數(shù)據(jù)變?yōu)楦俚牧械质沟脕G失的信息最小？到底如何度量丟失信息的多少？如何根據(jù)原始數(shù)據(jù)決定具體的降維操作步驟？

要回答上面的問(wèn)題，就要對(duì)降維問(wèn)題進(jìn)行數(shù)學(xué)化和形式化的討論。而PCA是一種具有嚴(yán)格數(shù)學(xué)基礎(chǔ)并且已被廣泛采用的降維方法。下面我不會(huì)直接描述PCA，而是通過(guò)逐步分析問(wèn)題，讓我們一起重新“發(fā)明”一遍PCA。

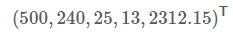
向量的表示及基變換

既然我們面對(duì)的數(shù)據(jù)被抽象為一組向量，那么下面有必要研究一些向量的數(shù)學(xué)性質(zhì)。而這些數(shù)學(xué)性質(zhì)將成為后續(xù)導(dǎo)出PCA的理論基礎(chǔ)。

內(nèi)積與投影

下面先來(lái)看一個(gè)高中就學(xué)過(guò)的向量運(yùn)算：內(nèi)積。兩個(gè)維數(shù)相同的向量的內(nèi)積被定義為：

內(nèi)積運(yùn)算將兩個(gè)向量映射為一個(gè)實(shí)數(shù)。其計(jì)算方式非常容易理解，但是其意義并不明顯。下面我們分析內(nèi)積的幾何意義。假設(shè)A和B是兩個(gè)n維向量，我們知道n維向量可以等價(jià)表示為n維空間中的一條從原點(diǎn)發(fā)射的有向線段，為了簡(jiǎn)單起見(jiàn)我們假設(shè)A和B均為二維向量，則A=(x1,y1)A=(x1,y1)，B=(x2,y2)B=(x2,y2)。則在二維平面上A和B可以用兩條發(fā)自原點(diǎn)的有向線段表示，見(jiàn)下圖：

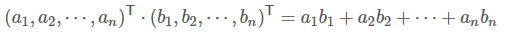
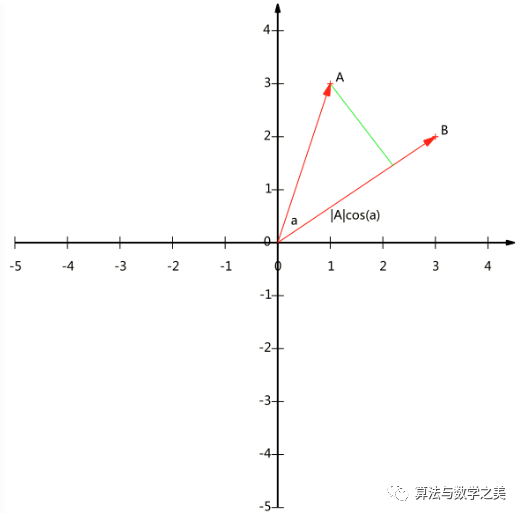
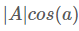好，現(xiàn)在我們從A點(diǎn)向B所在直線引一條垂線。我們知道垂線與B的交點(diǎn)叫做A在B上的投影，再設(shè)A與B的夾角是a，則投影的矢量長(zhǎng)度為其中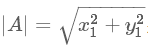

是向量A的模，也就是A線段的標(biāo)量長(zhǎng)度。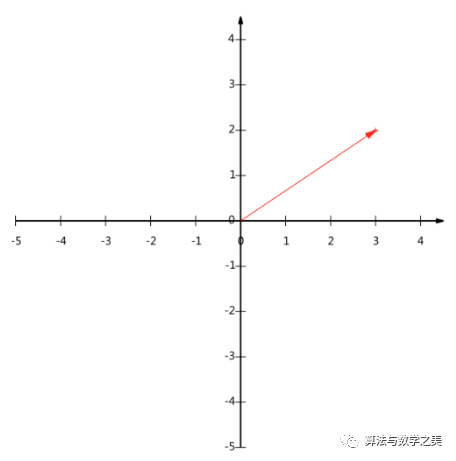

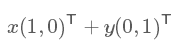
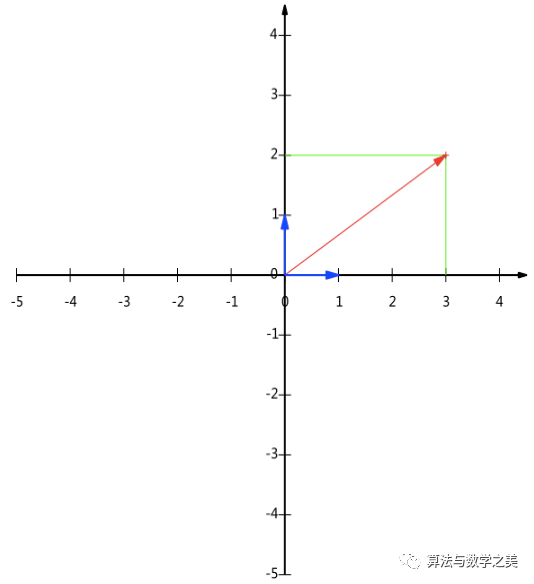
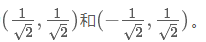
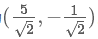
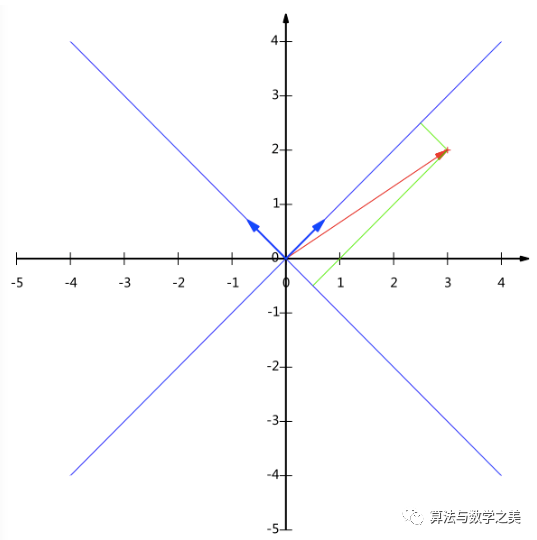
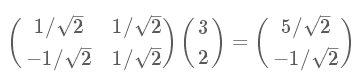
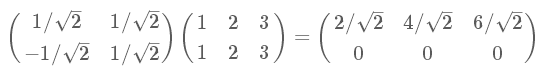
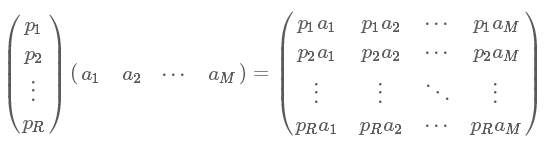
注意這里我們專(zhuān)門(mén)區(qū)分了矢量長(zhǎng)度和標(biāo)量長(zhǎng)度，標(biāo)量長(zhǎng)度總是大于等于0，值就是線段的長(zhǎng)度；而矢量長(zhǎng)度可能為負(fù)，其絕對(duì)值是線段長(zhǎng)度，而符號(hào)取決于其方向與標(biāo)準(zhǔn)方向相同或相反。

到這里還是看不出內(nèi)積和這東西有什么關(guān)系，不過(guò)如果我們將內(nèi)積表示為另一種我們熟悉的形式：

A?B=|A||B|cos(a)

現(xiàn)在事情似乎是有點(diǎn)眉目了：A與B的內(nèi)積等于A到B的投影長(zhǎng)度乘以B的模。再進(jìn)一步，如果我們假設(shè)B的模為1，即讓|B|=1，那么就變成了：

A?B=|A|cos(a)

也就是說(shuō)，設(shè)向量B的模為1，則A與B的內(nèi)積值等于A向B所在直線投影的矢量長(zhǎng)度！這就是內(nèi)積的一種幾何解釋?zhuān)彩俏覀兊玫降牡谝粋€(gè)重要結(jié)論。在后面的推導(dǎo)中，將反復(fù)使用這個(gè)結(jié)論。

基

下面我們繼續(xù)在二維空間內(nèi)討論向量。上文說(shuō)過(guò)，一個(gè)二維向量可以對(duì)應(yīng)二維笛卡爾直角坐標(biāo)系中從原點(diǎn)出發(fā)的一個(gè)有向線段。例如下面這個(gè)向量：

在代數(shù)表示方面，我們經(jīng)常用線段終點(diǎn)的點(diǎn)坐標(biāo)表示向量，例如上面的向量可以表示為(3,2)，這是我們?cè)偈煜げ贿^(guò)的向量表示。

不過(guò)我們常常忽略，只有一個(gè)(3,2)本身是不能夠精確表示一個(gè)向量的。我們仔細(xì)看一下，這里的3實(shí)際表示的是向量在x軸上的投影值是3，在y軸上的投影值是2。也就是說(shuō)我們其實(shí)隱式引入了一個(gè)定義：以x軸和y軸上正方向長(zhǎng)度為1的向量為標(biāo)準(zhǔn)。那么一個(gè)向量(3,2)實(shí)際是說(shuō)在x軸投影為3而y軸的投影為2。注意投影是一個(gè)矢量，所以可以為負(fù)。

更正式的說(shuō)，向量(x,y)實(shí)際上表示線性組合：

不難證明所有二維向量都可以表示為這樣的線性組合。此處(1,0)和(0,1)叫做二維空間中的一組基。

所以，要準(zhǔn)確描述向量，首先要確定一組基，然后給出在基所在的各個(gè)直線上的投影值，就可以了。只不過(guò)我們經(jīng)常省略第一步，而默認(rèn)以(1,0)和(0,1)為基。

我們之所以默認(rèn)選擇(1,0)和(0,1)為基，當(dāng)然是比較方便，因?yàn)樗鼈兎謩e是x和y軸正方向上的單位向量，因此就使得二維平面上點(diǎn)坐標(biāo)和向量一一對(duì)應(yīng)，非常方便。但實(shí)際上任何兩個(gè)線性無(wú)關(guān)的二維向量都可以成為一組基，所謂線性無(wú)關(guān)在二維平面內(nèi)可以直觀認(rèn)為是兩個(gè)不在一條直線上的向量。

例如，(1,1)和(-1,1)也可以成為一組基。一般來(lái)說(shuō)，我們希望基的模是1，因?yàn)閺膬?nèi)積的意義可以看到，如果基的模是1，那么就可以方便的用向量點(diǎn)乘基而直接獲得其在新基上的坐標(biāo)了！實(shí)際上，對(duì)應(yīng)任何一個(gè)向量我們總可以找到其同方向上模為1的向量，只要讓兩個(gè)分量分別除以模就好了。例如，上面的基可以變?yōu)?/span>

現(xiàn)在，我們想獲得(3,2)在新基上的坐標(biāo)，即在兩個(gè)方向上的投影矢量值，那么根據(jù)內(nèi)積的幾何意義，我們只要分別計(jì)算(3,2)和兩個(gè)基的內(nèi)積，不難得到新的坐標(biāo)為

下圖給出了新的基以及(3,2)在新基上坐標(biāo)值的示意圖：

另外這里要注意的是，我們列舉的例子中基是正交的（即內(nèi)積為0，或直觀說(shuō)相互垂直），但可以成為一組基的唯一要求就是線性無(wú)關(guān)，非正交的基也是可以的。不過(guò)因?yàn)檎换休^好的性質(zhì)，所以一般使用的基都是正交的。

基變換的矩陣表示

下面我們找一種簡(jiǎn)便的方式來(lái)表示基變換。還是拿上面的例子，想一下，將(3,2)變換為新基上的坐標(biāo)，就是用(3,2)與第一個(gè)基做內(nèi)積運(yùn)算，作為第一個(gè)新的坐標(biāo)分量，然后用(3,2)與第二個(gè)基做內(nèi)積運(yùn)算，作為第二個(gè)新坐標(biāo)的分量。實(shí)際上，我們可以用矩陣相乘的形式簡(jiǎn)潔的表示這個(gè)變換：

太漂亮了！其中矩陣的兩行分別為兩個(gè)基，乘以原向量，其結(jié)果剛好為新基的坐標(biāo)。可以稍微推廣一下，如果我們有m個(gè)二維向量，只要將二維向量按列排成一個(gè)兩行m列矩陣，然后用“基矩陣”乘以這個(gè)矩陣，就得到了所有這些向量在新基下的值。例如(1,1)，(2,2)，(3,3)，想變換到剛才那組基上，則可以這樣表示：

于是一組向量的基變換被干凈的表示為矩陣的相乘。

一般的，如果我們有M個(gè)N維向量，想將其變換為由R個(gè)N維向量表示的新空間中，那么首先將R個(gè)基按行組成矩陣A，然后將向量按列組成矩陣B，那么兩矩陣的乘積AB就是變換結(jié)果，其中AB的第m列為A中第m列變換后的結(jié)果。

數(shù)學(xué)表示為：

其中pi是一個(gè)行向量，表示第i個(gè)基，aj是一個(gè)列向量，表示第j個(gè)原始數(shù)據(jù)記錄

特別要注意的是，這里R可以小于N，而R決定了變換后數(shù)據(jù)的維數(shù)。也就是說(shuō)，我們可以將一N維數(shù)據(jù)變換到更低維度的空間中去，變換后的維度取決于基的數(shù)量。因此這種矩陣相乘的表示也可以表示降維變換。

最后，上述分析同時(shí)給矩陣相乘找到了一種物理解釋?zhuān)簝蓚€(gè)矩陣相乘的意義是將右邊矩陣中的每一列列向量變換到左邊矩陣中每一行行向量為基所表示的空間中去。更抽象的說(shuō)，一個(gè)矩陣可以表示一種線性變換。很多同學(xué)在學(xué)線性代數(shù)時(shí)對(duì)矩陣相乘的方法感到奇怪，但是如果明白了矩陣相乘的物理意義，其合理性就一目了然了。

協(xié)方差矩陣及優(yōu)化目標(biāo)

上面我們討論了選擇不同的基可以對(duì)同樣一組數(shù)據(jù)給出不同的表示，而且如果基的數(shù)量少于向量本身的維數(shù)，則可以達(dá)到降維的效果。但是我們還沒(méi)有回答一個(gè)最最關(guān)鍵的問(wèn)題：如何選擇基才是最優(yōu)的。或者說(shuō)，如果我們有一組N維向量，現(xiàn)在要將其降到K維（K小于N），那么我們應(yīng)該如何選擇K個(gè)基才能最大程度保留原有的信息？

要完全數(shù)學(xué)化這個(gè)問(wèn)題非常繁雜，這里我們用一種非形式化的直觀方法來(lái)看這個(gè)問(wèn)題。

為了避免過(guò)于抽象的討論，我們?nèi)砸砸粋€(gè)具體的例子展開(kāi)。假設(shè)我們的數(shù)據(jù)由五條記錄組成，將它們表示成矩陣形式：

其中每一列為一條數(shù)據(jù)記錄，而一行為一個(gè)字段。為了后續(xù)處理方便，我們首先將每個(gè)字段內(nèi)所有值都減去字段均值，其結(jié)果是將每個(gè)字段都變?yōu)榫禐?（這樣做的道理和好處后面會(huì)看到）。

我們看上面的數(shù)據(jù)，第一個(gè)字段均值為2，第二個(gè)字段均值為3，所以變換后：

我們可以看下五條數(shù)據(jù)在平面直角坐標(biāo)系內(nèi)的樣子：

現(xiàn)在問(wèn)題來(lái)了：如果我們必須使用一維來(lái)表示這些數(shù)據(jù)，又希望盡量保留原始的信息，你要如何選擇？

通過(guò)上一節(jié)對(duì)基變換的討論我們知道，這個(gè)問(wèn)題實(shí)際上是要在二維平面中選擇一個(gè)方向，將所有數(shù)據(jù)都投影到這個(gè)方向所在直線上，用投影值表示原始記錄。這是一個(gè)實(shí)際的二維降到一維的問(wèn)題。

那么如何選擇這個(gè)方向（或者說(shuō)基）才能盡量保留最多的原始信息呢？一種直觀的看法是：希望投影后的投影值盡可能分散。

以上圖為例，可以看出如果向x軸投影，那么最左邊的兩個(gè)點(diǎn)會(huì)重疊在一起，中間的兩個(gè)點(diǎn)也會(huì)重疊在一起，于是本身四個(gè)各不相同的二維點(diǎn)投影后只剩下兩個(gè)不同的值了，這是一種嚴(yán)重的信息丟失，同理，如果向y軸投影最上面的兩個(gè)點(diǎn)和分布在x軸上的兩個(gè)點(diǎn)也會(huì)重疊。所以看來(lái)x和y軸都不是最好的投影選擇。我們直觀目測(cè)，如果向通過(guò)第一象限和第三象限的斜線投影，則五個(gè)點(diǎn)在投影后還是可以區(qū)分的。

下面，我們用數(shù)學(xué)方法表述這個(gè)問(wèn)題。

方差

上文說(shuō)到，我們希望投影后投影值盡可能分散，而這種分散程度，可以用數(shù)學(xué)上的方差來(lái)表述。此處，一個(gè)字段的方差可以看做是每個(gè)元素與字段均值的差的平方和的均值，即：

由于上面我們已經(jīng)將每個(gè)字段的均值都化為0了，因此方差可以直接用每個(gè)元素的平方和除以元素個(gè)數(shù)表示：

于是上面的問(wèn)題被形式化表述為：尋找一個(gè)一維基，使得所有數(shù)據(jù)變換為這個(gè)基上的坐標(biāo)表示后，方差值最大。

協(xié)方差

對(duì)于上面二維降成一維的問(wèn)題來(lái)說(shuō)，找到那個(gè)使得方差最大的方向就可以了。不過(guò)對(duì)于更高維，還有一個(gè)問(wèn)題需要解決。考慮三維降到二維問(wèn)題。與之前相同，首先我們希望找到一個(gè)方向使得投影后方差最大，這樣就完成了第一個(gè)方向的選擇，繼而我們選擇第二個(gè)投影方向。

如果我們還是單純只選擇方差最大的方向，很明顯，這個(gè)方向與第一個(gè)方向應(yīng)該是“幾乎重合在一起”，顯然這樣的維度是沒(méi)有用的，因此，應(yīng)該有其他約束條件。從直觀上說(shuō)，讓兩個(gè)字段盡可能表示更多的原始信息，我們是不希望它們之間存在（線性）相關(guān)性的，因?yàn)橄嚓P(guān)性意味著兩個(gè)字段不是完全獨(dú)立，必然存在重復(fù)表示的信息。

數(shù)學(xué)上可以用兩個(gè)字段的協(xié)方差表示其相關(guān)性，由于已經(jīng)讓每個(gè)字段均值為0，則：

可以看到，在字段均值為0的情況下，兩個(gè)字段的協(xié)方差簡(jiǎn)潔的表示為其內(nèi)積除以元素?cái)?shù)m。

當(dāng)協(xié)方差為0時(shí)，表示兩個(gè)字段完全獨(dú)立。為了讓協(xié)方差為0，我們選擇第二個(gè)基時(shí)只能在與第一個(gè)基正交的方向上選擇。因此最終選擇的兩個(gè)方向一定是正交的。

至此，我們得到了降維問(wèn)題的優(yōu)化目標(biāo)：將一組N維向量降為K維（K大于0，小于N），其目標(biāo)是選擇K個(gè)單位（模為1）正交基，使得原始數(shù)據(jù)變換到這組基上后，各字段兩兩間協(xié)方差為0，而字段的方差則盡可能大（在正交的約束下，取最大的K個(gè)方差）。

協(xié)方差矩陣

上面我們導(dǎo)出了優(yōu)化目標(biāo)，但是這個(gè)目標(biāo)似乎不能直接作為操作指南（或者說(shuō)算法），因?yàn)樗徽f(shuō)要什么，但根本沒(méi)有說(shuō)怎么做。所以我們要繼續(xù)在數(shù)學(xué)上研究計(jì)算方案。

我們看到，最終要達(dá)到的目的與字段內(nèi)方差及字段間協(xié)方差有密切關(guān)系。因此我們希望能將兩者統(tǒng)一表示，仔細(xì)觀察發(fā)現(xiàn)，兩者均可以表示為內(nèi)積的形式，而內(nèi)積又與矩陣相乘密切相關(guān)。于是我們來(lái)了靈感：

假設(shè)我們只有a和b兩個(gè)字段，那么我們將它們按行組成矩陣X：

然后我們用X乘以X的轉(zhuǎn)置，并乘上系數(shù)1/m：

奇跡出現(xiàn)了！這個(gè)矩陣對(duì)角線上的兩個(gè)元素分別是兩個(gè)字段的方差，而其它元素是a和b的協(xié)方差。兩者被統(tǒng)一到了一個(gè)矩陣的。

根據(jù)矩陣相乘的運(yùn)算法則，這個(gè)結(jié)論很容易被推廣到一般情況：

設(shè)我們有m個(gè)n維數(shù)據(jù)記錄，將其按列排成n乘m的矩陣X，設(shè)

則C是一個(gè)對(duì)稱(chēng)矩陣，其對(duì)角線分別個(gè)各個(gè)字段的方差，而第i行j列和j行i列元素相同，表示i和j兩個(gè)字段的協(xié)方差。

協(xié)方差矩陣對(duì)角化

根據(jù)上述推導(dǎo)，我們發(fā)現(xiàn)要達(dá)到優(yōu)化目前，等價(jià)于將協(xié)方差矩陣對(duì)角化：即除對(duì)角線外的其它元素化為0，并且在對(duì)角線上將元素按大小從上到下排列，這樣我們就達(dá)到了優(yōu)化目的。這樣說(shuō)可能還不是很明晰，我們進(jìn)一步看下原矩陣與基變換后矩陣協(xié)方差矩陣的關(guān)系：

設(shè)原始數(shù)據(jù)矩陣X對(duì)應(yīng)的協(xié)方差矩陣為C，而P是一組基按行組成的

矩陣，設(shè)Y=PX，則Y為X對(duì)P做基變換后的數(shù)據(jù)。設(shè)Y的協(xié)方差矩陣為D，我們推導(dǎo)一下D與C的關(guān)系：

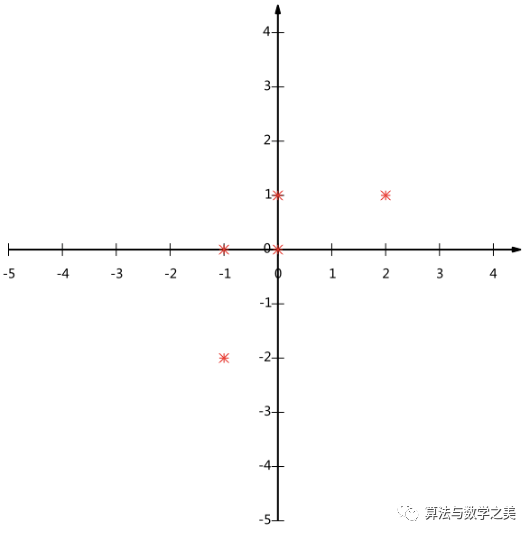
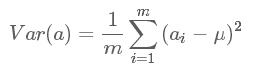
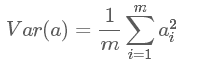
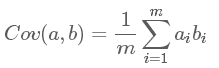
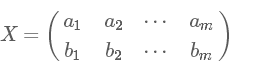
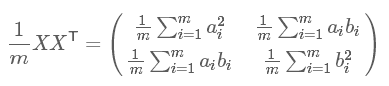
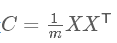
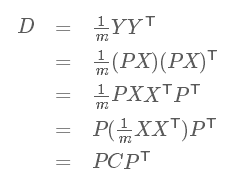
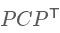現(xiàn)在事情很明白了！我們要找的P不是別的，而是能讓原始協(xié)方差矩陣對(duì)角化的P。換句話說(shuō)，優(yōu)化目標(biāo)變成了尋找一個(gè)矩陣P，滿足 是一個(gè)對(duì)角矩陣，并且對(duì)角元素按從大到小依次排列，那么P的前K行就是要尋找的基，用P的前K行組成的矩陣乘以X就使得X從N維降到了K維并滿足上述優(yōu)化條件。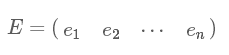

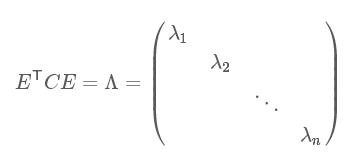
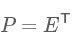
至此，我們離“發(fā)明”P(pán)CA還有僅一步之遙！

現(xiàn)在所有焦點(diǎn)都聚焦在了協(xié)方差矩陣對(duì)角化問(wèn)題上，有時(shí)，我們真應(yīng)該感謝數(shù)學(xué)家的先行，因?yàn)榫仃噷?duì)角化在線性代數(shù)領(lǐng)域已經(jīng)屬于被玩爛了的東西，所以這在數(shù)學(xué)上根本不是問(wèn)題。

由上文知道，協(xié)方差矩陣C是一個(gè)是對(duì)稱(chēng)矩陣，在線性代數(shù)上，實(shí)對(duì)稱(chēng)矩陣有一系列非常好的性質(zhì)：

1）實(shí)對(duì)稱(chēng)矩陣不同特征值對(duì)應(yīng)的特征向量必然正交。

2）設(shè)特征向量λ重?cái)?shù)為r，則必然存在r個(gè)線性無(wú)關(guān)的特征向量對(duì)應(yīng)于λλ，因此可以將這r個(gè)特征向量單位正交化。

由上面兩條可知，一個(gè)n行n列的實(shí)對(duì)稱(chēng)矩陣一定可以找到n個(gè)單位正交特征向量，設(shè)這n個(gè)特征向量為e1,e2,?,en，我們將其按列組成矩陣：

則對(duì)協(xié)方差矩陣C有如下結(jié)論：

其中Λ為對(duì)角矩陣，其對(duì)角元素為各特征向量對(duì)應(yīng)的特征值（可能有重復(fù)）。

以上結(jié)論不再給出嚴(yán)格的數(shù)學(xué)證明，對(duì)證明感興趣的朋友可以參考線性代數(shù)書(shū)籍關(guān)于“實(shí)對(duì)稱(chēng)矩陣對(duì)角化”的內(nèi)容。

到這里，我們發(fā)現(xiàn)我們已經(jīng)找到了需要的矩陣P:

P是協(xié)方差矩陣的特征向量單位化后按行排列出的矩陣，其中每一行都是C的一個(gè)特征向量。如果設(shè)P按照Λ中特征值的從大到小，將特征向量從上到下排列，則用P的前K行組成的矩陣乘以原始數(shù)據(jù)矩陣X，就得到了我們需要的降維后的數(shù)據(jù)矩陣Y。

至此我們完成了整個(gè)PCA的數(shù)學(xué)原理討論。在下面的一節(jié)，我們將給出PCA的一個(gè)實(shí)例。

算法及實(shí)例

為了鞏固上面的理論，我們?cè)谶@一節(jié)給出一個(gè)具體的PCA實(shí)例。

PCA算法

總結(jié)一下PCA的算法步驟：

設(shè)有m條n維數(shù)據(jù)。

1）將原始數(shù)據(jù)按列組成n行m列矩陣X

2）將X的每一行（代表一個(gè)屬性字段）進(jìn)行零均值化，即減去這一行的均值

3）求出協(xié)方差矩陣

4）求出協(xié)方差矩陣的特征值及對(duì)應(yīng)的特征向量

5）將特征向量按對(duì)應(yīng)特征值大小從上到下按行排列成矩陣，取前k行組成矩陣P

6）Y=PX即為降維到k維后的數(shù)據(jù)

實(shí)例

這里是上文提到的

為例，我們用PCA方法將這組二維數(shù)據(jù)其降到一維。

因?yàn)檫@個(gè)矩陣的每行已經(jīng)是零均值，這里我們直接求協(xié)方差矩陣：

然后求其特征值和特征向量，具體求解方法不再詳述，可以參考相關(guān)資料。求解后特征值為：

其對(duì)應(yīng)的特征向量分別是：

其中對(duì)應(yīng)的特征向量分別是一個(gè)通解，c1c1和c2c2可取任意實(shí)數(shù)。那么標(biāo)準(zhǔn)化后的特征向量為：

因此我們的矩陣P是：

可以驗(yàn)證協(xié)方差矩陣C的對(duì)角化：

最后我們用P的第一行乘以數(shù)據(jù)矩陣，就得到了降維后的表示：

降維投影結(jié)果如下圖：

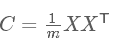
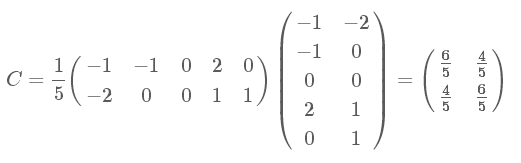
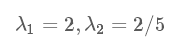
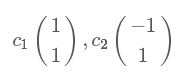
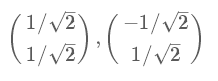
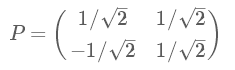
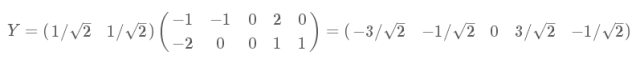
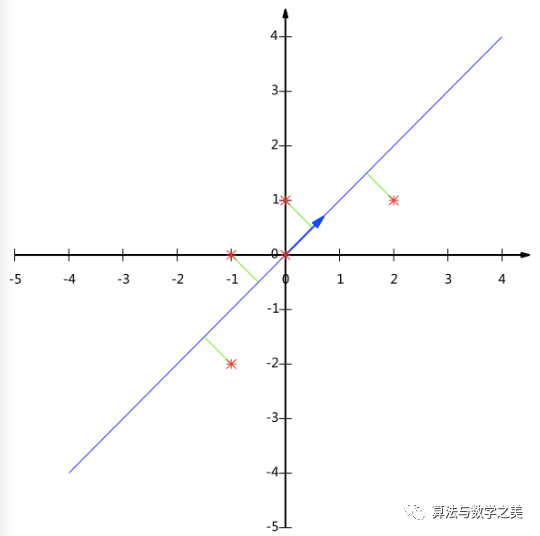
進(jìn)一步討論

根據(jù)上面對(duì)PCA的數(shù)學(xué)原理的解釋?zhuān)覀兛梢粤私獾揭恍㏄CA的能力和限制。PCA本質(zhì)上是將方差最大的方向作為主要特征，并且在各個(gè)正交方向上將數(shù)據(jù)“離相關(guān)”，也就是讓它們?cè)诓煌环较蛏蠜](méi)有相關(guān)性。

因此，PCA也存在一些限制，例如它可以很好的解除線性相關(guān)，但是對(duì)于高階相關(guān)性就沒(méi)有辦法了，對(duì)于存在高階相關(guān)性的數(shù)據(jù)，可以考慮Kernel PCA，通過(guò)Kernel函數(shù)將非線性相關(guān)轉(zhuǎn)為線性相關(guān)，關(guān)于這點(diǎn)就不展開(kāi)討論了。另外，PCA假設(shè)數(shù)據(jù)各主特征是分布在正交方向上，如果在非正交方向上存在幾個(gè)方差較大的方向，PCA的效果就大打折扣了。

最后需要說(shuō)明的是，PCA是一種無(wú)參數(shù)技術(shù)，也就是說(shuō)面對(duì)同樣的數(shù)據(jù)，如果不考慮清洗，誰(shuí)來(lái)做結(jié)果都一樣，沒(méi)有主觀參數(shù)的介入，所以PCA便于通用實(shí)現(xiàn)，但是本身無(wú)法個(gè)性化的優(yōu)化。

希望這篇文章能幫助朋友們了解PCA的數(shù)學(xué)理論基礎(chǔ)和實(shí)現(xiàn)原理，借此了解PCA的適用場(chǎng)景和限制，從而更好的使用這個(gè)算法。 

— THE END —

?概率的意義：隨機(jī)世界與大數(shù)法則

?詳解凸優(yōu)化、圖神經(jīng)網(wǎng)絡(luò)、強(qiáng)化學(xué)習(xí)、貝葉斯方法等四大主題

?大學(xué)數(shù)學(xué)不好，或許是數(shù)學(xué)教材的鍋？

?數(shù)學(xué)與國(guó)家實(shí)力

?x背后的軼聞趣事

?瞎扯數(shù)學(xué)分析-微積分（1~4）