獲取神經(jīng)網(wǎng)絡(luò)的計(jì)算量和參數(shù)量

作者：DengBoCong 文僅交流，侵刪

Github：本文代碼放在該項(xiàng)目中：https://github.com/DengBoCong/nlp-paper

說(shuō)明：講解時(shí)會(huì)對(duì)相關(guān)文章資料進(jìn)行思想、結(jié)構(gòu)、優(yōu)缺點(diǎn)，內(nèi)容進(jìn)行提煉和記錄，相關(guān)引用會(huì)標(biāo)明出處，引用之處如有侵權(quán)，煩請(qǐng)告知?jiǎng)h除。

目錄：

• 全連接層的計(jì)算量和參數(shù)量估計(jì)

• 激活函數(shù)的計(jì)算量估計(jì)

• LSTM的計(jì)算量和參數(shù)量估計(jì)

• 卷積層的計(jì)算量和參數(shù)量估計(jì)

• 深度可分離卷積的計(jì)算量和參數(shù)量估計(jì)

• Batch Normalization的計(jì)算量和參數(shù)量估計(jì)

• 其他層的計(jì)算量和參數(shù)量估計(jì)

對(duì)于深度學(xué)習(xí)模型來(lái)說(shuō)，擁有一個(gè)非常好的設(shè)計(jì)思路和體系架構(gòu)非常重要，對(duì)模型性能的影響非常之大，所以對(duì)于模型的研究?jī)A向于在模型性能上的表現(xiàn)。但是對(duì)于商業(yè)應(yīng)用來(lái)說(shuō)，算法模型落地的另一個(gè)重要考量就是在滿足業(yè)務(wù)場(chǎng)景內(nèi)存占用、計(jì)算量等需要的同時(shí)，保證算法的性能，這個(gè)研究對(duì)于移動(dòng)端的模型部署更加明顯，這有利于壓縮應(yīng)用的體積。最近這段時(shí)間正好在研究關(guān)于移動(dòng)端模型部署（TensorFlow Lite用的不是很順心呀），所以要仔細(xì)研究一下模型的參數(shù)量等，這不僅可以讓我們對(duì)模型的大小進(jìn)行了解，還能更好的調(diào)整結(jié)構(gòu)使得模型響應(yīng)的更快。

可能有時(shí)候覺(jué)得，模型的大小需要計(jì)算嘛，直接保存大小直接看不就完事兒了？運(yùn)行速度就更直接了，多運(yùn)行幾次取平均速度不就行了嘛?so easy？這個(gè)想法也沒(méi)啥錯(cuò)，但是大前提是你得有個(gè)整型的模型呀（訓(xùn)練成本多高心里沒(méi)數(shù)嘛），因此很多時(shí)候我們想要在模型設(shè)計(jì)之初就估計(jì)一下模型的大小以及可能的運(yùn)行速度（通過(guò)一些指標(biāo)側(cè)面反應(yīng)速度），這個(gè)時(shí)候我們就需要更深入的理解模型的內(nèi)部結(jié)構(gòu)和原理，從而通過(guò)估算模型內(nèi)部的參數(shù)量和計(jì)算量來(lái)對(duì)模型的大小和速度進(jìn)行一個(gè)初步評(píng)估。

一個(gè)樸素的評(píng)估模型速度的想法是評(píng)估它的計(jì)算量。一般我們用FLOPS，即每秒浮點(diǎn)操作次數(shù)FLoating point OPerations per Second這個(gè)指標(biāo)來(lái)衡量GPU的運(yùn)算能力。這里我們用MACC，即乘加數(shù)Multiply-ACCumulate operation，或者叫MADD，來(lái)衡量模型的計(jì)算量。不過(guò)這里要說(shuō)明一下，用MACC來(lái)估算模型的計(jì)算量只能大致地估算一下模型的速度。模型最終的的速度，不僅僅是和計(jì)算量多少有關(guān)系，還和諸如內(nèi)存帶寬、優(yōu)化程度、CPU流水線、Cache之類(lèi)的因素也有很大關(guān)系。

下面我們對(duì)計(jì)算量來(lái)進(jìn)行介紹和定義，方便我們后續(xù)展開(kāi)層的講解：

神經(jīng)網(wǎng)絡(luò)中的許多計(jì)算都是點(diǎn)積，例如：

y = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + ... + w[n-1]*x[n-1]

此處，  和  是兩個(gè)向量，結(jié)果  是標(biāo)量（單個(gè)數(shù)字）。對(duì)于卷積層或完全連接的層（現(xiàn)代神經(jīng)網(wǎng)絡(luò)中兩種主要類(lèi)型的層），  是該層的學(xué)習(xí)權(quán)重，  是該層的輸入。我們將  計(jì)數(shù)為一個(gè)乘法累加或1個(gè)MACC，這里的“累加”運(yùn)算是加法運(yùn)算，因?yàn)槲覀儗⑺谐朔ǖ慕Y(jié)果相加，所以上式具有  個(gè)這樣的MACC（從技術(shù)上講，上式中只有  個(gè)加法，比乘法數(shù)少一個(gè)，所以這里知識(shí)認(rèn)為MACC的數(shù)量是一個(gè)近似值）。就FLOPS而言，因?yàn)橛?nbsp; 個(gè)乘法和  個(gè)加法，所以點(diǎn)積執(zhí)行  FLOPS，因此，MACC大約是兩個(gè)FLOPS。現(xiàn)在，我們來(lái)看幾種不同的層類(lèi)型，以了解如何計(jì)算這些層的MACC數(shù)量。

注意了：下面的闡述如果沒(méi)有特別說(shuō)明，默認(rèn)都是batch為1。

01

在完全連接的層中，所有輸入都連接到所有輸出。對(duì)于具有  輸入值和  輸出值的圖層，其權(quán)重  可以存儲(chǔ)在  矩陣中。全連接層執(zhí)行的計(jì)算為：

在這里，  是  輸入值的向量，  是包含圖層權(quán)重的  矩陣，  是  偏差值的向量，這些值也被相加。結(jié)果  包含由圖層計(jì)算的輸出值，并且也是大小  的向量。對(duì)于完全連接層來(lái)說(shuō)，矩陣乘法為  ，其中具有  個(gè)MACC（和權(quán)重矩陣  大小一樣），對(duì)于偏置  ，正好補(bǔ)齊了前面我們所說(shuō)的點(diǎn)積中正好少一個(gè)加法操作。因此，比如一個(gè)具有300個(gè)輸入神經(jīng)元和100個(gè)輸出神經(jīng)元的全連接層執(zhí)行  個(gè)MACC。特別提示：上面我們討論的批次大小  需要具體計(jì)算需要乘上Batch。

也就是說(shuō)，通常，將長(zhǎng)度為  的向量與  矩陣相乘以獲得長(zhǎng)度為  的向量，則需要  MACC或  FLOPS。

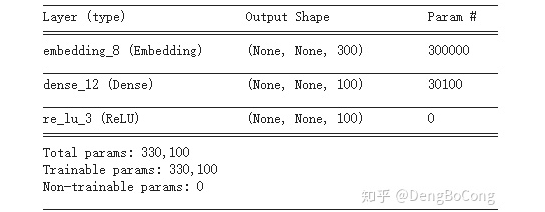
上面我們討論了全連接層的計(jì)算量，那么它的參數(shù)量是多少呢？這個(gè)應(yīng)該很容易就算出來(lái)，對(duì)于全連接層而言，它的參數(shù)分別是權(quán)重  和 偏置  ，所以對(duì)于上面的例子中具有300個(gè)輸入神經(jīng)元和100個(gè)輸出神經(jīng)元的全連接層的參數(shù)量是：  ，這個(gè)很容易進(jìn)行驗(yàn)證，下圖是使用TensorFlow進(jìn)行驗(yàn)證參數(shù)量：

02

通常，一個(gè)層后面緊接著就是非線性激活函數(shù)，例如ReLU或sigmoid，理所當(dāng)然的計(jì)算這些激活函數(shù)需要時(shí)間，但在這里我們不用MACC進(jìn)行度量，而是使用FLOPS進(jìn)行度量，原因是它們不做點(diǎn)積，一些激活函數(shù)比其他激活函數(shù)更難計(jì)算，例如一個(gè)ReLU只是：

這是在GPU上的一項(xiàng)操作，激活函數(shù)僅應(yīng)用于層的輸出，例如在具有  個(gè)輸出神經(jīng)元的完全連接層上，ReLU計(jì)算  次，因此我們將其判定為  FLOPS。而對(duì)于Sigmoid激活函數(shù)來(lái)說(shuō)，有不一樣了，它涉及到了一個(gè)指數(shù)，所以成本更高：

在計(jì)算FLOPS時(shí)，我們通常將加，減，乘，除，求冪，平方根等作為單個(gè)FLOP進(jìn)行計(jì)數(shù)，由于在Sigmoid激活函數(shù)中有四個(gè)不同的運(yùn)算，因此將其判定為每個(gè)函數(shù)輸出4 FLOPS或總層輸出  FLOPS。所以實(shí)際上，通常不計(jì)這些操作，因?yàn)樗鼈冎徽伎倳r(shí)間的一小部分，更多時(shí)候我們主要對(duì)（大）矩陣乘法和點(diǎn)積感興趣，所以其實(shí)我們通常都是忽略激活函數(shù)的計(jì)算量。

對(duì)于參數(shù)量？注意了它壓根沒(méi)有參數(shù)，請(qǐng)看它們的公式，用TensorFlow驗(yàn)證如下：

03

關(guān)于LSTM的原理可以參考這一篇文章

http://colah.github.io/posts/2015-08-Understanding-LSTMs/

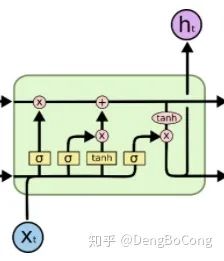
實(shí)際上LSTM里面有 4 個(gè)非線性變換（3 個(gè) 門(mén) + 1 個(gè) tanh），每一個(gè)非線性變換說(shuō)白了就是一個(gè)全連接網(wǎng)絡(luò)，形如：  。其中，第一層是  和  的結(jié)合，維度就是embedding_size + hidden_size，第二層就是輸出層，維度為 hidden_size，則它的計(jì)算量按照上文我們對(duì)全連接層的闡述，易得MACC為：

(embedding_size + hidden_size) * hidden_size * 4

四個(gè)非線性變換中，還會(huì)對(duì)全連接層的輸出進(jìn)行激活函數(shù)計(jì)算（三個(gè)sigmoid和一個(gè)tanh），由上面討論的sigmoid我們知道，對(duì)于sigmoid的計(jì)算量為：(embedding_size + hidden_size) * hidden_size * 3 *4個(gè)FLOPS，而tanh的計(jì)算公式為：  ，其中共有八個(gè)加，減，乘，除，求冪，平方根等計(jì)算，所以計(jì)算量為：(embedding_size + hidden_size) * hidden_size * 8個(gè)FLOPS。除此之外，LSTM除了在四個(gè)非線性變換中的計(jì)算，還有三個(gè)矩陣乘法（不是點(diǎn)積）、一個(gè)加法、一個(gè)tanh計(jì)算，其中三個(gè)矩陣乘法都是shape為(batch, hidden_size)，則這四個(gè)運(yùn)算的計(jì)算量為：batch * hidden_size + batch * hidden_size + batch * hidden_size + batch * hidden_size + batch * hidden_size * 8，綜上所述，LSTM的計(jì)算量為：

(embedding_size + hidden_size) * hidden_size * 4 個(gè)MACCembedding_size * hidden_size * 8 + hidden_size * (hidden_size + 20) 個(gè)FLOPS

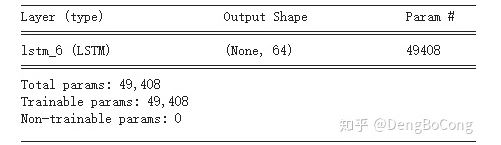
((embedding_size + hidden_size) * hidden_size + hidden_size) * 4

對(duì)于特征維128的輸入，LSTM單元數(shù)為64的網(wǎng)絡(luò)來(lái)說(shuō)，LSTM的參數(shù)量為：((128 + 64) * 64 + 64) * 4 = 49408，通過(guò)TensorFlow驗(yàn)證如下：

04

卷積層的輸入和輸出不是矢量，而是shape為  的三維特征圖，其中  是特征圖的高度，  是寬度，  是每個(gè)位置的通道數(shù)，正如我們所見(jiàn)今天使用的大多數(shù)卷積層都是二維正方內(nèi)核，對(duì)于內(nèi)核大小為  的轉(zhuǎn)換層，MACC的數(shù)量為：

• 輸出特征圖中有Hout × Wout × Cout個(gè)像素；
• 每個(gè)像素對(duì)應(yīng)一個(gè)立體卷積核K x K x Cin在輸入特征圖上做立體卷積卷積出來(lái)的；
• 而這個(gè)立體卷積操作，卷積核上每個(gè)點(diǎn)都對(duì)應(yīng)一次MACC操作

同樣，我們?cè)谶@里為了方便忽略了偏置和激活。我們不應(yīng)該忽略的是層的stride，以及任何dilation因子，padding等。這就是為什么我們需要參看層的輸出特征圖的尺寸Hout × Wout，因它考慮到了stride等因素。比如，對(duì)于  ，128個(gè)filter的卷積，在  帶有64個(gè)通道的輸入特征圖上，我們執(zhí)行MACC的次數(shù)是：

這幾乎是10億次累積運(yùn)算！注意：在此示例中，我們使用“same”填充和  ，以便輸出特征圖與輸入特征圖具有相同的大小。通常看到卷積層使用  ，這會(huì)將輸出特征圖大小減少一半，在上面的計(jì)算中，我們將使用  而不是  。

根據(jù)卷積的原理，對(duì)于上面的例子中，  ，128個(gè)filter的卷積，在  帶有64個(gè)通道的輸入特征圖上的參數(shù)量為：  ，用TensorFlow驗(yàn)證結(jié)果如下圖：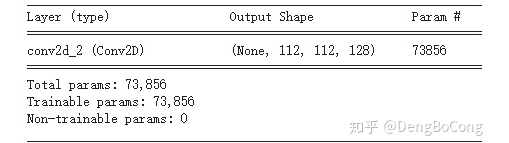

05

這減少了  的工作量，比常規(guī)的卷積層效率更高。當(dāng)然，僅深度卷積是不夠的，我們還需要增加“可分離”，第二個(gè)操作是常規(guī)卷積，但始終使用內(nèi)核大小  ，即  ，也稱(chēng)為“逐點(diǎn)”卷積，MACC的數(shù)量為：

深度可分離卷積分為兩個(gè)操作，深度卷積和可分離，所以現(xiàn)在我們對(duì)兩種操作分別就上面的例子計(jì)算，和并和常規(guī)  卷積進(jìn)行比較：

3×3 depthwise          : 7,225,3441×1 pointwise          : 102,760,448深度可分離卷積          : 109,985,792 MACCs
常規(guī) 3×3 卷積           : 924,844,032 MACCs

• 一個(gè)  卷積，為特征圖添加更多通道（稱(chēng)為expansion layer）
•  深度卷積，用于過(guò)濾數(shù)據(jù)（depthwise convolution）
•  卷積，再次減少通道數(shù)（projection layer，bottleneck convolution）

•  ，(參照上面?zhèn)鹘y(tǒng)卷積，把卷積核設(shè)置為1x1即得)
•  (參照MoblieNet V1分析)
• (參照MoblieNet V1分析，或者傳統(tǒng)卷積把卷積核設(shè)置為1x1即得)

這與MobileNet V1使用的深度可分層相比如何？如果我們使用輸入特征圖  擴(kuò)展因子6，以及  的  深度卷積和128輸出通道，那么MACC的總數(shù)是：

這不是比以前更多嗎？是的，它甚至超過(guò)了最初的  卷積。但是......請(qǐng)注意，由于擴(kuò)展層，在這個(gè)塊內(nèi)，我們實(shí)際上使用了  通道。因此，這組層比原始的  卷積做得更多（從64到128個(gè)通道），而計(jì)算成本大致相同。

06

此處，  是上一層的輸出圖中的元素。我們首先通過(guò)減去該輸出通道的平均值并除以標(biāo)準(zhǔn)偏差來(lái)對(duì)該值進(jìn)行歸一化（epsilon 用于確保不除以0，通常為0.001），然后，我們將系數(shù)gamma縮放，然后添加一個(gè)偏差或偏移beta。每個(gè)通道都有自己的gamma，beta，均值和方差值，因此，如果卷積層的輸出中有  個(gè)通道，則Batch normalization層將學(xué)習(xí)  參數(shù)，如下圖所示：

07

示例：在  具有128通道的特征圖上具有過(guò)濾器大小2和步幅2的最大池化層需要  FLOPS或1.6兆FLOPS。當(dāng)然，如果步幅與濾波器尺寸不同（例如  窗口，  步幅），則這些數(shù)字會(huì)稍微改變。

08

• 減少參數(shù)
• 降低精度
• 融合計(jì)算單元步驟

https://www.jianshu.com/p/b8d48c99a47chttp://machinethink.net/blog/how-fast-is-my-model/http://colah.github.io/posts/2015-08-Understanding-LSTMs/https://datascience.stackexchange.com/questions/10615/number-of-parameters-in-an-lstm-modelhttps://zhuanlan.zhihu.com/p/77471991https://arxiv.org/abs/1506.02626

猜您喜歡：

等你著陸！【GAN生成對(duì)抗網(wǎng)絡(luò)】知識(shí)星球！

超100篇！CVPR 2020最全GAN論文梳理匯總！

附下載 | 《Python進(jìn)階》中文版

附下載 | 經(jīng)典《Think Python》中文版

附下載 | 《Pytorch模型訓(xùn)練實(shí)用教程》

附下載 | 最新2020李沐《動(dòng)手學(xué)深度學(xué)習(xí)》

附下載 | 《可解釋的機(jī)器學(xué)習(xí)》中文版

附下載 |《TensorFlow 2.0 深度學(xué)習(xí)算法實(shí)戰(zhàn)》

附下載 | 超100篇！CVPR 2020最全GAN論文梳理匯總！

附下載 |《計(jì)算機(jī)視覺(jué)中的數(shù)學(xué)方法》分享