【機(jī)器學(xué)習(xí)】機(jī)器學(xué)習(xí)算法 隨機(jī)森林學(xué)習(xí) 之決策樹
隨機(jī)森林是基于集體智慧的一個機(jī)器學(xué)習(xí)算法,也是目前最好的機(jī)器學(xué)習(xí)算法之一。
隨機(jī)森林實(shí)際是一堆決策樹的組合(正如其名,樹多了就是森林了)。在用于分類一個新變量時,相關(guān)的檢測數(shù)據(jù)提交給構(gòu)建好的每個分類樹。每個樹給出一個分類結(jié)果,最終選擇被最多的分類樹支持的分類結(jié)果。回歸則是不同樹預(yù)測出的值的均值。
要理解隨機(jī)森林,我們先學(xué)習(xí)下決策樹。
決策樹 - 把你做選擇的過程呈現(xiàn)出來
決策樹是一個很直觀的跟我們?nèi)粘W鲞x擇的思維方式很相近的一個算法。
如果有一個數(shù)據(jù)集如下:
data <- data.frame(x=c(0,0.5,1.1,1.8,1.9,2,2.5,3,3.6,3.7), color=c(rep('blue',5),rep('green',5)))
data
## x color
## 1 0.0 blue
## 2 0.5 blue
## 3 1.1 blue
## 4 1.8 blue
## 5 1.9 blue
## 6 2.0 green
## 7 2.5 green
## 8 3.0 green
## 9 3.6 green
## 10 3.7 green那么假如加入一個新的點(diǎn),其x值為1,那么該點(diǎn)對應(yīng)的最可能的顏色是什么?
根據(jù)上面的數(shù)據(jù)找規(guī)律,如果x<2.0則對應(yīng)的點(diǎn)顏色為blue,如果x>=2.0則對應(yīng)的點(diǎn)顏色為green。這就構(gòu)成了一個只有一個決策節(jié)點(diǎn)的簡單決策樹。
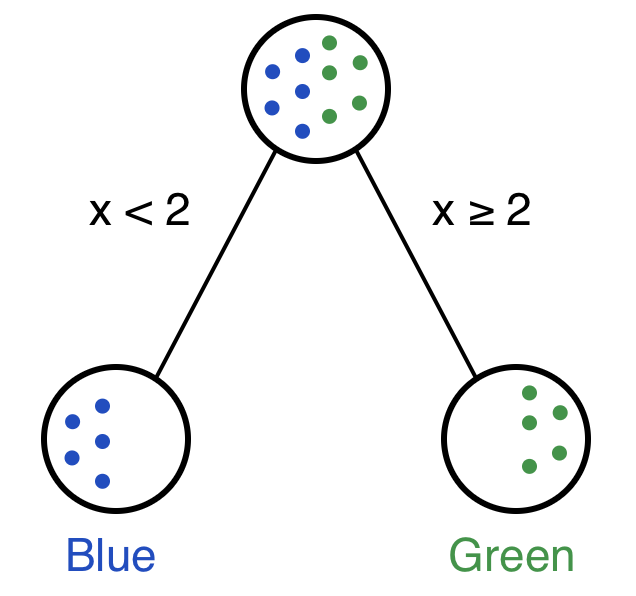
決策樹常用來回答這樣的問題:給定一個帶標(biāo)簽的數(shù)據(jù)集(標(biāo)簽這里對應(yīng)我們的color列),怎么來對新加入的數(shù)據(jù)集進(jìn)行分類?
如果數(shù)據(jù)集再復(fù)雜一些,如下,
data <- data.frame(x=c(0,0.5,1.1,1.8,1.9,2,2.5,3,3.6,3.7),
y=c(1,0.5,1.5,2.1,2.8,2,2.2,3,3.3,3.5),
color=c(rep('blue',3),rep('red',2),rep('green',5)))
data
## x y color
## 1 0.0 1.0 blue
## 2 0.5 0.5 blue
## 3 1.1 1.5 blue
## 4 1.8 2.1 red
## 5 1.9 2.8 red
## 6 2.0 2.0 green
## 7 2.5 2.2 green
## 8 3.0 3.0 green
## 9 3.6 3.3 green
## 10 3.7 3.5 green如果
x>=2.0則對應(yīng)的點(diǎn)顏色為green。如果
x<2.0則對應(yīng)的點(diǎn)顏色可能為blue,也可能為red。
這時就需要再加一個新的決策節(jié)點(diǎn),利用變量y的信息。
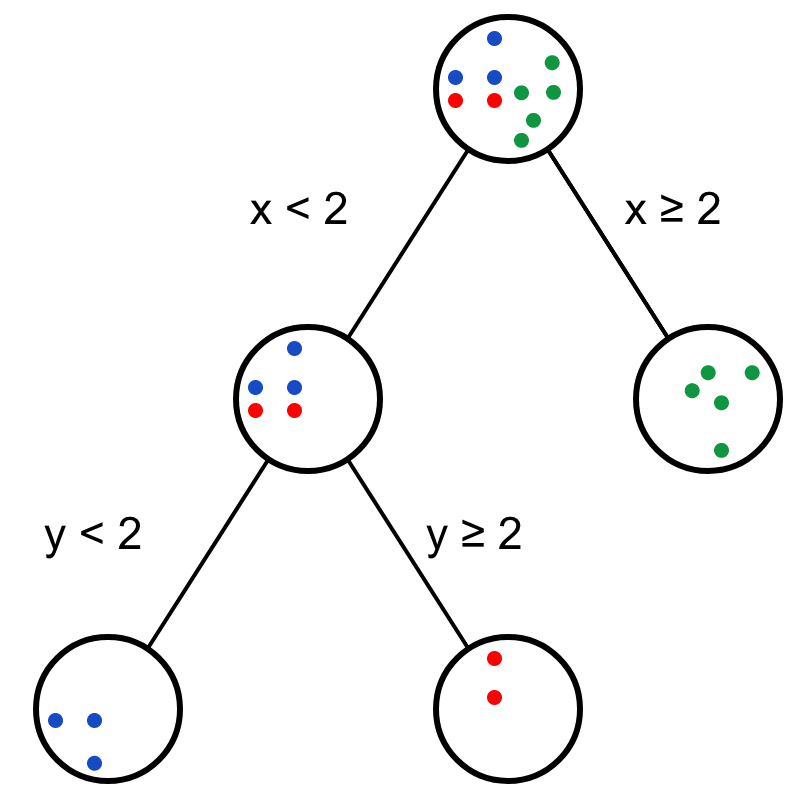
這就是決策樹,也是我們?nèi)粘M评韱栴}的一般方式。
訓(xùn)練決策樹 - 確定決策樹的根節(jié)點(diǎn)
第一個任務(wù)是確定決策樹的根節(jié)點(diǎn):選擇哪個變量和對應(yīng)閾值選擇多少能給數(shù)據(jù)做出最好的區(qū)分。
比如上面的例子,我們可以先處理變量x,選擇閾值為2 (為什么選2,是不是有比2更合適閾值,我們后續(xù)再說),則可獲得如下分類:
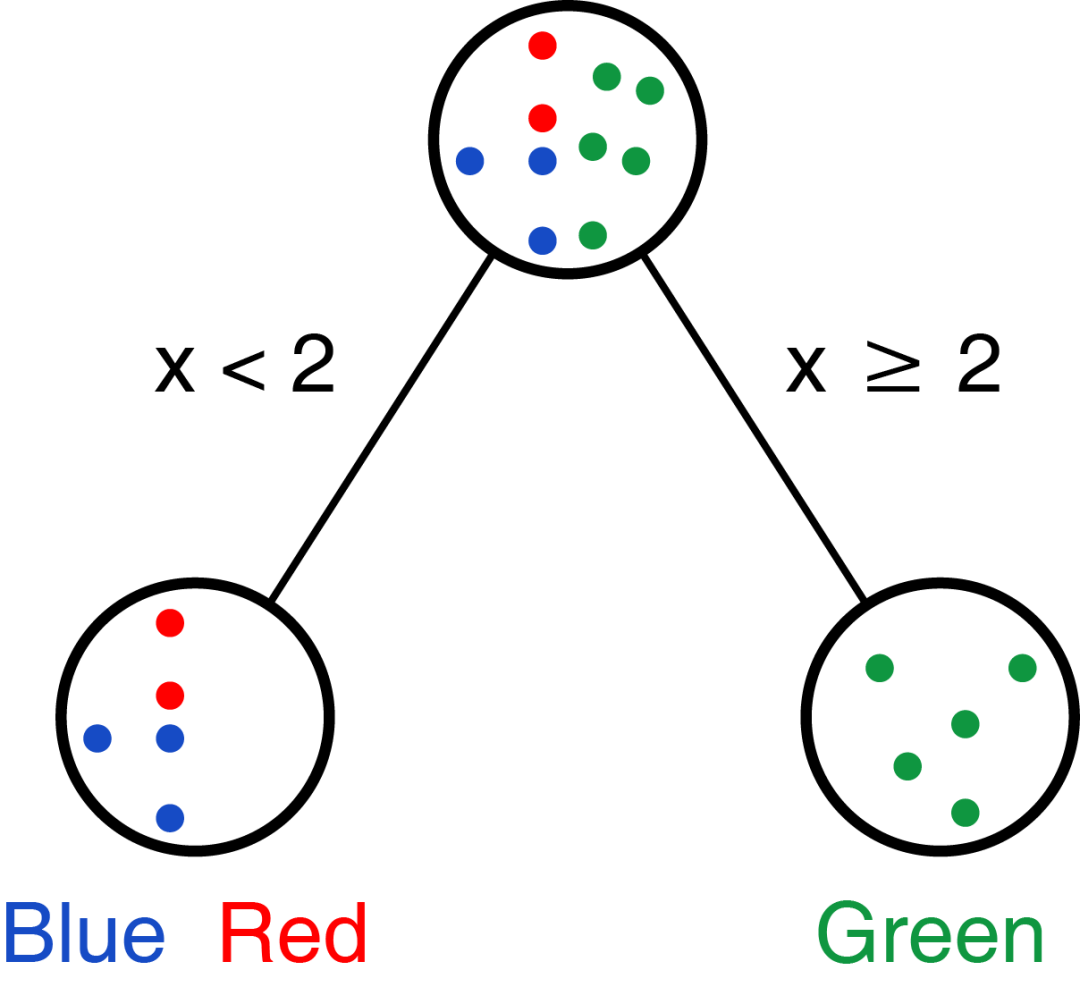
我們也可以先處理變量y,選擇閾值為2,則可獲得如下分類:
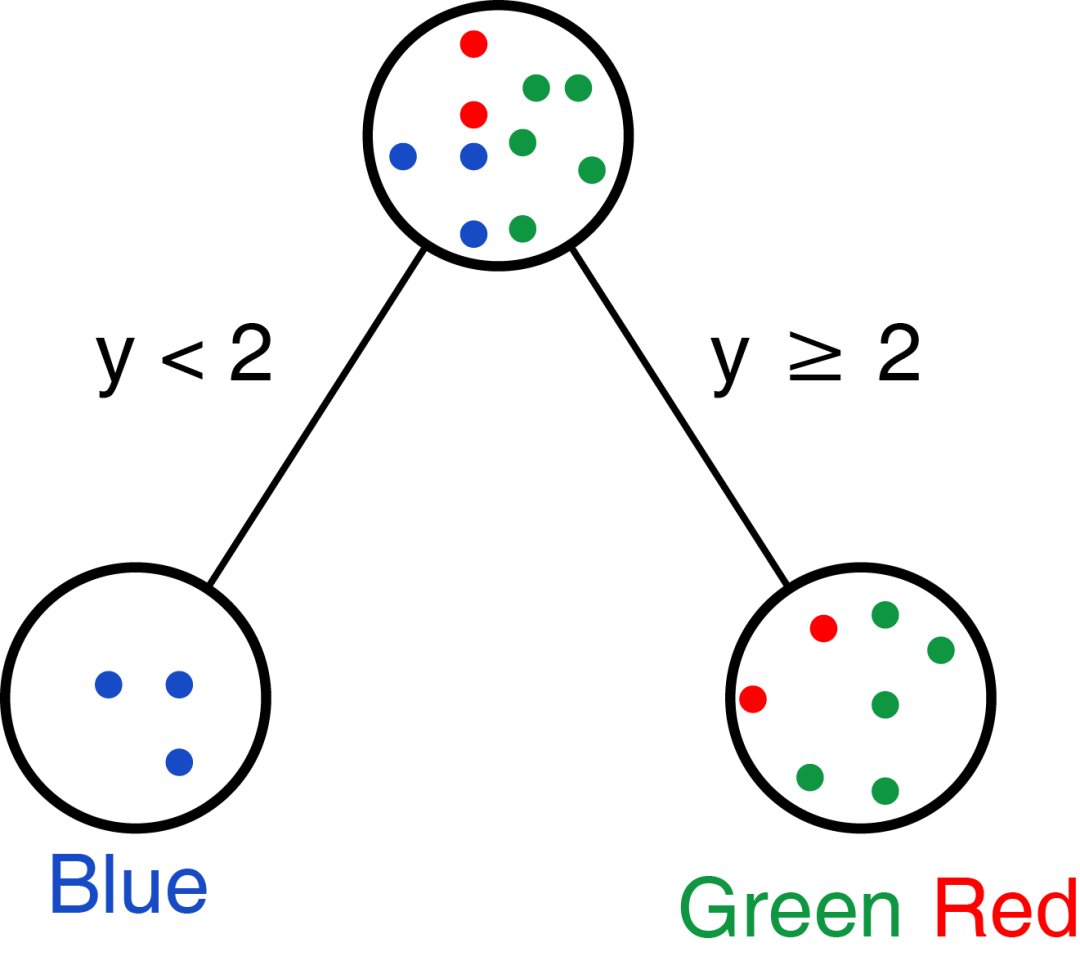
那實(shí)際需要選擇哪個呢?
實(shí)際我們是希望每個選擇的變量和閾值能把不同的類分的越開越好;上面選擇變量x分組時,Green完全分成一組;下面選擇y分組時,Blue完全分成一組。怎么評價呢?
這時就需要一個評價指標(biāo),常用的指標(biāo)有Gini inpurity和Information gain。
Gini Impurity
在數(shù)據(jù)集中隨機(jī)選擇一個數(shù)據(jù)點(diǎn),并隨機(jī)分配給它一個數(shù)據(jù)集中存在的標(biāo)簽,分配錯誤的概率即為Gini impurity。
我們先看第一套數(shù)據(jù)集,10個數(shù)據(jù)點(diǎn),5個blue,5個green。從中隨機(jī)選一個數(shù)據(jù)點(diǎn),再隨機(jī)選一個分類標(biāo)簽作為這個數(shù)據(jù)點(diǎn)的標(biāo)簽,分類錯誤的概率是多少?如下表,錯誤概率為0.25+0.25=0.5(看下面的計(jì)算過程)。
probility <- data.frame(Event=c("Pick Blue, Classify Blue",
"Pick Blue, Classify Green",
"Pick Green, Classify Blue",
"Pick Green, Classify Green"),
Probability=c(5/10 * 5/10, 5/10 * 5/10, 5/10 * 5/10, 5/10 * 5/10),
Type=c("Blue" == "Blue",
"Blue" == "Green",
"Green" == "Blue",
"Green" == "Green"))
probility
## Event Probability Type
## 1 Pick Blue, Classify Blue 0.25 TRUE
## 2 Pick Blue, Classify Green 0.25 FALSE
## 3 Pick Green, Classify Blue 0.25 FALSE
## 4 Pick Green, Classify Green 0.25 TRUE我們再看第二套數(shù)據(jù)集,10個數(shù)據(jù)點(diǎn),2個red,3個blue,5個green。從中隨機(jī)選一個數(shù)據(jù)點(diǎn),再隨機(jī)選一個分類標(biāo)簽作為這個數(shù)據(jù)點(diǎn)的標(biāo)簽,分類錯誤的概率是多少?0.62。
probility <- data.frame(Event=c("Pick Blue, Classify Blue",
"Pick Blue, Classify Green",
"Pick Blue, Classify Red",
"Pick Green, Classify Blue",
"Pick Green, Classify Green",
"Pick Green, Classify Red",
"Pick Red, Classify Blue",
"Pick Red, Classify Green",
"Pick Red, Classify Red"
),
Probability=c(3/10 * 3/10, 3/10 * 5/10, 3/10 * 2/10,
5/10 * 3/10, 5/10 * 5/10, 5/10 * 2/10,
2/10 * 3/10, 2/10 * 5/10, 2/10 * 2/10),
Type=c("Blue" == "Blue",
"Blue" == "Green",
"Blue" == "Red",
"Green" == "Blue",
"Green" == "Green",
"Green" == "Red",
"Red" == "Blue",
"Red" == "Green",
"Red" == "Red"
))
probility
## Event Probability Type
## 1 Pick Blue, Classify Blue 0.09 TRUE
## 2 Pick Blue, Classify Green 0.15 FALSE
## 3 Pick Blue, Classify Red 0.06 FALSE
## 4 Pick Green, Classify Blue 0.15 FALSE
## 5 Pick Green, Classify Green 0.25 TRUE
## 6 Pick Green, Classify Red 0.10 FALSE
## 7 Pick Red, Classify Blue 0.06 FALSE
## 8 Pick Red, Classify Green 0.10 FALSE
## 9 Pick Red, Classify Red 0.04 TRUE
Wrong_probability = sum(probility[!probility$Type,"Probability"])
Wrong_probability
## [1] 0.62Gini Impurity計(jì)算公式:
假如我們的數(shù)據(jù)點(diǎn)共有C個類,p(i)是從中隨機(jī)拿到一個類為i的數(shù)據(jù),Gini Impurity計(jì)算公式為:
$$ G = \sum_{i=1}^{C} p(i)*(1-p(i)) $$

對第一套數(shù)據(jù)集,10個數(shù)據(jù)點(diǎn),5個blue,5個green。從中隨機(jī)選一個數(shù)據(jù)點(diǎn),再隨機(jī)選一個分類標(biāo)簽作為這個數(shù)據(jù)點(diǎn)的標(biāo)簽,分類錯誤的概率是多少?錯誤概率為0.25+0.25=0.5。
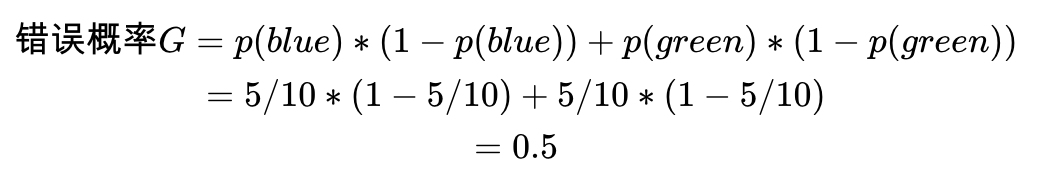
對第二套數(shù)據(jù)集,10個數(shù)據(jù)點(diǎn),2個red,3個blue,5個green。
從中隨機(jī)選一個數(shù)據(jù)點(diǎn),再隨機(jī)選一個分類標(biāo)簽作為這個數(shù)據(jù)點(diǎn)的標(biāo)簽,分類錯誤的概率是多少?0.62。

決策樹分類后的Gini Impurity
對第一套數(shù)據(jù)集來講,按照x<2分成兩個分支,各個分支都只包含一個分類數(shù)據(jù),各自的Gini
IMpurity值為0。
這是一個完美的決策樹,把Gini Impurity為0.5的數(shù)據(jù)集分類為2個Gini Impurity為0的數(shù)據(jù)集。Gini Impurity==?0是能獲得的最好的分類結(jié)果。


第二套數(shù)據(jù)集,我們有兩種確定根節(jié)點(diǎn)的方式,哪一個更優(yōu)呢?
我們可以先處理變量x,選擇閾值為2,則可獲得如下分類:

每個分支的Gini Impurity可以如下計(jì)算:
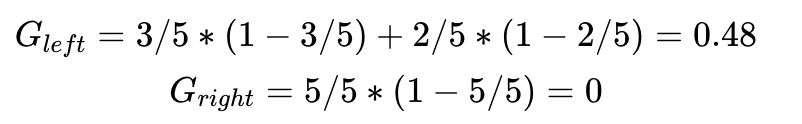
當(dāng)前決策的Gini impurity需要對各個分支包含的數(shù)據(jù)點(diǎn)的比例進(jìn)行加權(quán),即
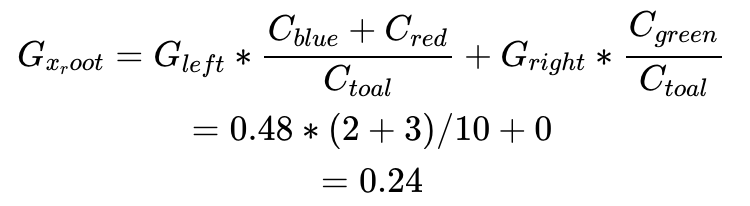
我們也可以先處理變量y,選擇閾值為2,則可獲得如下分類:

每個分支的Gini Impurity可以如下計(jì)算:
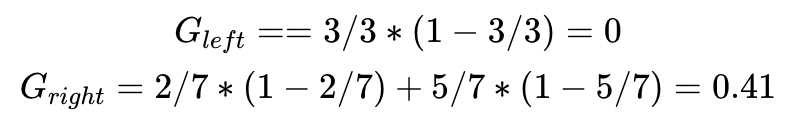
當(dāng)前決策的Gini impurity需要對各個分支包含的數(shù)據(jù)點(diǎn)的比例進(jìn)行加權(quán),即

兩個數(shù)值比較0.24<0.29,選擇x作為第一個分類節(jié)點(diǎn)是我們第二套數(shù)據(jù)第一步?jīng)Q策樹的最佳選擇。
前面手算單個變量、單個分組不算麻煩,也是個學(xué)習(xí)的過程。后續(xù)如果有更多變量和閾值時,再手算就不合適了。下一篇我們通過暴力方式自寫函數(shù)訓(xùn)練決策樹。
當(dāng)前計(jì)算的結(jié)果,可以作為正對照,確定后續(xù)函數(shù)結(jié)果的準(zhǔn)確性。
訓(xùn)練決策樹 - 確定根節(jié)點(diǎn)的分類閾值
Gini impurity可以用來判斷每一步最合適的決策分類方式,那么怎么確定最優(yōu)的分類變量和分類閾值呢?
最粗暴的方式是,我們用每個變量的每個可能得閾值來進(jìn)行決策分類,選擇具有最低Gini impurity值的分類組合。這不是最快速的解決問題的方式,但是最容易理解的方式。
定義計(jì)算Gini impurity的函數(shù)
data <- data.frame(x=c(0,0.5,1.1,1.8,1.9,2,2.5,3,3.6,3.7),
y=c(1,0.5,1.5,2.1,2.8,2,2.2,3,3.3,3.5),
color=c(rep('blue',3),rep('red',2),rep('green',5)))
data
## x y color
## 1 0.0 1.0 blue
## 2 0.5 0.5 blue
## 3 1.1 1.5 blue
## 4 1.8 2.1 red
## 5 1.9 2.8 red
## 6 2.0 2.0 green
## 7 2.5 2.2 green
## 8 3.0 3.0 green
## 9 3.6 3.3 green
## 10 3.7 3.5 green首先定義個函數(shù)計(jì)算Gini_impurity。
Gini_impurity <- function(branch){
# print(branch)
len_branch <- length(branch)
if(len_branch==0){
return(0)
}
table_branch <- table(branch)
wrong_probability <- function(x, total) (x/total*(1-x/total))
return(sum(sapply(table_branch, wrong_probability, total=len_branch)))
}測試下,沒問題。
Gini_impurity(c(rep('a',2),rep('b',3)))
## [1] 0.48再定義一個函數(shù),計(jì)算每次決策的總Gini impurity.
Gini_impurity_for_split_branch <- function(threshold, data, variable_column,
class_column, Init_gini_impurity=NULL){
total = nrow(data)
left <- data[data[variable_column]<threshold,][[class_column]]
left_len = length(left)
left_table = table(left)
left_gini <- Gini_impurity(left)
right <- data[data[variable_column]>=threshold,][[class_column]]
right_len = length(right)
right_table = table(right)
right_gini <- Gini_impurity(right)
total_gini <- left_gini * left_len / total + right_gini * right_len /total
result = c(variable_column,threshold,
paste(names(left_table), left_table, collapse="; ", sep=" x "),
paste(names(right_table), right_table, collapse="; ", sep=" x "),
total_gini)
names(result) <- c("Variable", "Threshold", "Left_branch", "Right_branch", "Gini_impurity")
if(!is.null(Init_gini_impurity)){
Gini_gain <- Init_gini_impurity - total_gini
result = c(variable_column, threshold,
paste(names(left_table), left_table, collapse="; ", sep=" x "),
paste(names(right_table), right_table, collapse="; ", sep=" x "),
Gini_gain)
names(result) <- c("Variable", "Threshold", "Left_branch", "Right_branch", "Gini_gain")
}
return(result)
}測試下,跟之前計(jì)算的結(jié)果一致:
as.data.frame(rbind(Gini_impurity_for_split_branch(2, data, 'x', 'color'),
Gini_impurity_for_split_branch(2, data, 'y', 'color')))
## Variable Threshold Left_branch Right_branch Gini_impurity
## 1 x 2 blue x 3; red x 2 green x 5 0.24
## 2 y 2 blue x 3 green x 5; red x 2 0.285714285714286暴力決策根節(jié)點(diǎn)和閾值
基于前面定義的函數(shù),遍歷每一個可能得變量和閾值。
首先看下基于變量x的計(jì)算方法:
uniq_x <- sort(unique(data$x))
delimiter_x <- zoo::rollmean(uniq_x,2)
impurity_x <- as.data.frame(do.call(rbind, lapply(delimiter_x, Gini_impurity_for_split_branch,
data=data, variable_column='x', class_column='color')))
print(impurity_x)
## Variable Threshold Left_branch Right_branch Gini_impurity
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2 0.533333333333333
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2 0.425
## 3 x 1.45 blue x 3 green x 5; red x 2 0.285714285714286
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1 0.316666666666667
## 5 x 1.95 blue x 3; red x 2 green x 5 0.24
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4 0.366666666666667
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3 0.457142857142857
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2 0.525
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1 0.577777777777778再包裝2個函數(shù),一個計(jì)算單個變量為節(jié)點(diǎn)的各種可能決策的Gini impurity,
另一個計(jì)算所有變量依次作為節(jié)點(diǎn)的各種可能決策的Gini impurity。
Gini_impurity_for_all_possible_branches_of_one_variable <- function(data, variable, class, Init_gini_impurity=NULL){
uniq_value <- sort(unique(data[[variable]]))
delimiter_value <- zoo::rollmean(uniq_value,2)
impurity <- as.data.frame(do.call(rbind, lapply(delimiter_value,
Gini_impurity_for_split_branch, data=data,
variable_column=variable,
class_column=class,
Init_gini_impurity=Init_gini_impurity)))
if(is.null(Init_gini_impurity)){
decreasing = F
} else {
decreasing = T
}
impurity <- impurity[order(impurity[[colnames(impurity)[5]]], decreasing = decreasing),]
return(impurity)
}
Gini_impurity_for_all_possible_branches_of_all_variables <- function(data, variables, class, Init_gini_impurity=NULL){
one_split_gini <- do.call(rbind, lapply(variables,
Gini_impurity_for_all_possible_branches_of_one_variable,
data=data, class=class,
Init_gini_impurity=Init_gini_impurity))
if(is.null(Init_gini_impurity)){
decreasing = F
} else {
decreasing = T
}
one_split_gini[order(one_split_gini[[colnames(one_split_gini)[5]]], decreasing = decreasing),]
}測試下:
Gini_impurity_for_all_possible_branches_of_one_variable(data, 'x', 'color')
## Variable Threshold Left_branch Right_branch Gini_impurity
## 5 x 1.95 blue x 3; red x 2 green x 5 0.24
## 3 x 1.45 blue x 3 green x 5; red x 2 0.285714285714286
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1 0.316666666666667
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4 0.366666666666667
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2 0.425
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3 0.457142857142857
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2 0.525
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2 0.533333333333333
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1 0.577777777777778兩個變量的各個閾值分別進(jìn)行決策,并計(jì)算Gini impurity,輸出按Gini impurity由小到大排序后的結(jié)果。根據(jù)變量x和閾值1.95(與上面選擇的閾值2獲得的決策結(jié)果一致)的決策可以獲得本步?jīng)Q策的最好結(jié)果。
variables <- c('x', 'y')
Gini_impurity_for_all_possible_branches_of_all_variables(data, variables, class="color")
## Variable Threshold Left_branch Right_branch Gini_impurity
## 5 x 1.95 blue x 3; red x 2 green x 5 0.24
## 3 x 1.45 blue x 3 green x 5; red x 2 0.285714285714286
## 31 y 1.75 blue x 3 green x 5; red x 2 0.285714285714286
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1 0.316666666666667
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4 0.366666666666667
## 41 y 2.05 blue x 3; green x 1 green x 4; red x 2 0.416666666666667
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2 0.425
## 21 y 1.25 blue x 2 blue x 1; green x 5; red x 2 0.425
## 51 y 2.15 blue x 3; green x 1; red x 1 green x 4; red x 1 0.44
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3 0.457142857142857
## 71 y 2.9 blue x 3; green x 2; red x 2 green x 3 0.457142857142857
## 61 y 2.5 blue x 3; green x 2; red x 1 green x 3; red x 1 0.516666666666667
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2 0.525
## 81 y 3.15 blue x 3; green x 3; red x 2 green x 2 0.525
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2 0.533333333333333
## 11 y 0.75 blue x 1 blue x 2; green x 5; red x 2 0.533333333333333
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1 0.577777777777778
## 91 y 3.4 blue x 3; green x 4; red x 2 green x 1 0.577777777777778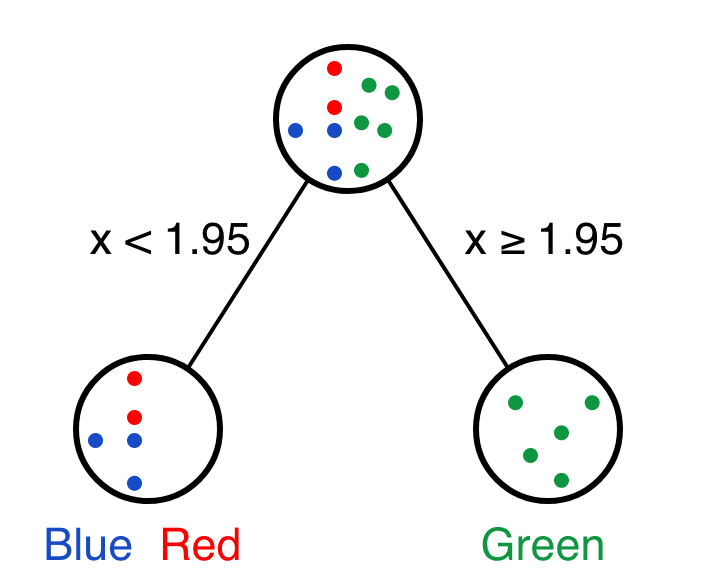
再決策第二個節(jié)點(diǎn)、第三個節(jié)點(diǎn)
第一個決策節(jié)點(diǎn)找好了,后續(xù)再找其它決策節(jié)點(diǎn)。如果某個分支的點(diǎn)從屬于多個class,則遞歸決策。
遞歸決策終止的條件是:
再添加分支不會降低
Gini impurity某個分支的數(shù)據(jù)點(diǎn)屬于同一分類組 (
Gini impurity = 0)
brute_descition_tree_result <- list()
brute_descition_tree_result_index <- 0
brute_descition_tree <- function(data, measure_variable, class_variable, type="Root"){
Init_gini_impurity <- Gini_impurity(data[[class_variable]])
brute_force_result <- Gini_impurity_for_all_possible_branches_of_all_variables(
data, variables, class=class_variable, Init_gini_impurity=Init_gini_impurity)
print(brute_force_result)
split_variable <- brute_force_result[1,1]
split_threshold <- brute_force_result[1,2]
gini_gain = brute_force_result[1,5]
# print(gini_gain)
left <- data[data[split_variable]<split_threshold,]
right <- data[data[split_variable]>=split_threshold,]
if(gini_gain>0){
brute_descition_tree_result_index <<- brute_descition_tree_result_index + 1
brute_descition_tree_result[[brute_descition_tree_result_index]] <<-
c(type=type, split_variable=split_variable,
split_threshold=split_threshold)
# print(brute_descition_tree_result_index)
# print(brute_descition_tree_result)
if(length(unique(left[[class_variable]]))>1){
brute_descition_tree(data=left, measure_variable, class_variable,
type=paste(brute_descition_tree_result_index, "left"))
}
if(length(unique(right[[class_variable]]))>1){
brute_descition_tree(data=right, measure_variable, class_variable,
type=paste(brute_descition_tree_result_index, "right"))
}
}
# return(brute_descition_tree_result)
}
brute_descition_tree(data, variables, "color")
## Variable Threshold Left_branch Right_branch Gini_gain
## 5 x 1.95 blue x 3; red x 2 green x 5 0.38
## 3 x 1.45 blue x 3 green x 5; red x 2 0.334285714285714
## 31 y 1.75 blue x 3 green x 5; red x 2 0.334285714285714
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1 0.303333333333333
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4 0.253333333333333
## 41 y 2.05 blue x 3; green x 1 green x 4; red x 2 0.203333333333333
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2 0.195
## 21 y 1.25 blue x 2 blue x 1; green x 5; red x 2 0.195
## 51 y 2.15 blue x 3; green x 1; red x 1 green x 4; red x 1 0.18
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3 0.162857142857143
## 71 y 2.9 blue x 3; green x 2; red x 2 green x 3 0.162857142857143
## 61 y 2.5 blue x 3; green x 2; red x 1 green x 3; red x 1 0.103333333333333
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2 0.095
## 81 y 3.15 blue x 3; green x 3; red x 2 green x 2 0.095
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2 0.0866666666666667
## 11 y 0.75 blue x 1 blue x 2; green x 5; red x 2 0.0866666666666667
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1 0.0422222222222223
## 91 y 3.4 blue x 3; green x 4; red x 2 green x 1 0.0422222222222223
## Variable Threshold Left_branch Right_branch Gini_gain
## 3 x 1.45 blue x 3 red x 2 0.48
## 31 y 1.8 blue x 3 red x 2 0.48
## 2 x 0.8 blue x 2 blue x 1; red x 2 0.213333333333333
## 21 y 1.25 blue x 2 blue x 1; red x 2 0.213333333333333
## 4 x 1.85 blue x 3; red x 1 red x 1 0.18
## 41 y 2.45 blue x 3; red x 1 red x 1 0.18
## 1 x 0.25 blue x 1 blue x 2; red x 2 0.08
## 11 y 0.75 blue x 1 blue x 2; red x 2 0.08
as.data.frame(do.call(rbind, brute_descition_tree_result))
## type split_variable split_threshold
## 1 Root x 1.95
## 2 2 left x 1.45運(yùn)行后,獲得兩個決策節(jié)點(diǎn),繪制決策樹如下:
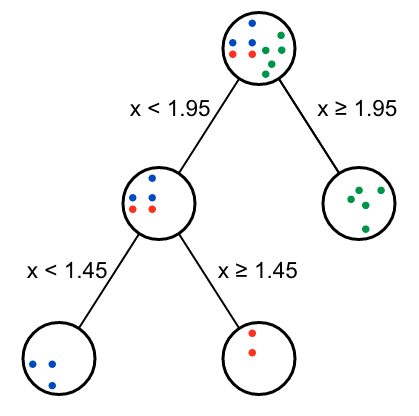
從返回的Gini gain表格可以看出,第二個節(jié)點(diǎn)有兩種效果一樣的分支方式。
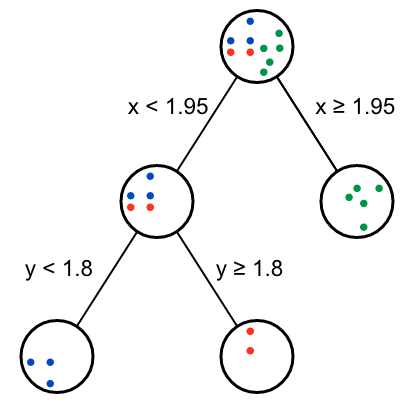
這樣我們就用暴力方式完成了決策樹的構(gòu)建。
隨機(jī)森林
data2 <- data.frame(x=c(0.4,0.8,1.1,1.1,1.2,1.3,2.3,2.4,3), y=c(2.9,0.8,1.8,2.4,2.3,1.2,2.1,3,1.2), color=c(rep(‘blue’,3),rep(‘red’,3),rep(‘green’,3)))
original_gini <- Gini_impurity(data2$color)
uniq_x <- sort(unique(data2$x))
delimiter_x <- zoo::rollmean(uniq_x,2)
t(sapply(delimiter_x, split_branch_gini, data=data2, variable_column='x', class_column='color', original_gini=original_gini))
library(rpart)
library(rpart.plot)
library(rattle)
fit <- rpart(color ~ x, data = data)
fancyRpartPlot(fit)
plot(fit, branch = 1)https://victorzhou.com/blog/intro-to-random-forests/
https://victorzhou.com/blog/gini-impurity/
https://stats.stackexchange.com/questions/192310/is-random-forest-suitable-for-very-small-data-sets
https://towardsdatascience.com/understanding-random-forest-58381e0602d2
https://www.stat.berkeley.edu/~breiman/RandomForests/reg_philosophy.html
https://medium.com/@williamkoehrsen/random-forest-simple-explanation-377895a60d2d
往期精彩回顧 本站qq群851320808,加入微信群請掃碼:
