程序員的數(shù)學(xué)課:如何優(yōu)化復(fù)雜度
嗨,我是你穩(wěn)定更新、持續(xù)輸出的勾勾。

今天學(xué)點算法叭!
復(fù)雜度
復(fù)雜度是程序時間損耗和數(shù)據(jù)總量之間的變化關(guān)系,通常用 O(f(n))?來表示,其中 f(n)?就是復(fù)雜度函數(shù)。
如果程序的時間損耗和數(shù)據(jù)量的關(guān)系是 t=c+n×b,也就是說復(fù)雜度函數(shù)為 f(n)=c+n×b。
復(fù)雜度通常不關(guān)注常數(shù),因為它是個固定的時間損耗,與輸入的數(shù)據(jù)總量沒有任何的關(guān)系。因此,復(fù)雜度函數(shù) c+n×b 可以忽略常數(shù) c 和 b,直接縮寫為 f(n) = n,即第一個例子的復(fù)雜度為 O(n)。
如果程序的時間損耗和數(shù)據(jù)量沒有關(guān)系,即 t=c,我們依然會忽略這個常數(shù),直接用 O(1)?來表示。
復(fù)雜度的計算與程序的結(jié)構(gòu)有著密切關(guān)系。通常而言,一個順序結(jié)構(gòu)或選擇結(jié)構(gòu)的代碼的執(zhí)行時間與數(shù)據(jù)量無關(guān),復(fù)雜度就是 O(1);而對于循環(huán)結(jié)構(gòu)而言,如果循環(huán)的次數(shù)與輸入數(shù)據(jù)量的多少有關(guān),就會產(chǎn)生復(fù)雜度了。
通常,一層循環(huán)的時間復(fù)雜度是 O(n);如果是兩個循環(huán)的嵌套,時間復(fù)雜度是 O(n2);如果是三個循環(huán)的嵌套,則是 O(n^3)……
用數(shù)學(xué)來優(yōu)化復(fù)雜度
設(shè)想一下,如果一段線上代碼在輸入變量很多的時候就會“卡死”,那么這一定是一款無法上線的系統(tǒng)。因此,時間復(fù)雜度的優(yōu)化,是每個開發(fā)者必須具備的技能。
其實,時間復(fù)雜度的優(yōu)化有很多辦法。除了優(yōu)化數(shù)據(jù)結(jié)構(gòu)、優(yōu)化代碼結(jié)構(gòu)、減少程序中不必要的計算等通用方法以外,還可以利用強大的數(shù)學(xué)知識來進行時間復(fù)雜度的優(yōu)化。
我們來舉幾個例子。
在一個無序的數(shù)組中,只有一個數(shù)字 obj 出現(xiàn)了一次,其他數(shù)字都出現(xiàn)了兩次,嘗試去查找出這個出現(xiàn)了一次的 obj。
絕大多數(shù)程序員的代碼邏輯,應(yīng)該都是設(shè)計兩層 for 循環(huán):一層遍歷每個數(shù)字,一層計算每個數(shù)字出現(xiàn)的次數(shù),直到找到 obj。
代碼如下:
a = [2,1,4,3,4,2,3]for i in range(0,len(a)):times = 0for j in range(0,len(a)):if a[i] == a[j]:times += 1if times == 1:print a[i]break
讀代碼:
第 2 行,開始 for 循環(huán),并把計數(shù)的變量 times 置為?0;
第 4 行,嵌套了一個 for 循環(huán);
第 5 行開始,判斷里外兩層循環(huán)的值是否相等,如果相等,則 times 加 1;
第 7 行,判斷 times 是否為 1,如果為 1 說明 a[i]?在數(shù)組中只出現(xiàn)了一次,則打印并 break 跳出循環(huán)結(jié)束。
根據(jù)我們前面的結(jié)論,這段代碼的復(fù)雜度是 O(n^2),而且單獨借助數(shù)據(jù)結(jié)構(gòu)等思想已經(jīng)很難再進行程序的優(yōu)化了。
然而,如果從數(shù)學(xué)視角來看,這段代碼就可以進行如下優(yōu)化:
a = [2,1,4,3,4,2,3]result = a[0]for i in range(1,len(a)):result = result ^ a[i]print result
在這里,利用了異或運算的性質(zhì):
滿足交換律和結(jié)合律;
可以把相同元素計算為?0;
0?異或任何數(shù)字都是其本身。
這樣,只要把數(shù)組 a 中所有元素都異或在一起,就得到了 obj。
此時,只需要一層 for 循環(huán),復(fù)雜度是 O(n)。
我們再看下面一個例子。
輸入一個正整數(shù) n,求不大于 n 的所有偶數(shù)之和。例如輸入 6,則輸出 2、4、6 之和,為 12;輸入5,則輸出 2、4 之和,為 6。
這個題目的常規(guī)解法,是采用 for 循環(huán),讓 i 從 1 遍歷到 n。如果 i 為奇數(shù),則 continue;如果為偶數(shù),則加到 result 變量中。
不難發(fā)現(xiàn),復(fù)雜度是 O(n),代碼如下:
import sysn = int(sys.argv[1])result = 0for i in range(n+1):if i % 2 == 0:result += iprint result
我們再從數(shù)學(xué)的視角來看待這個問題,你就會發(fā)現(xiàn)這是個等差數(shù)列求和的問題,等差數(shù)列求和的公式為
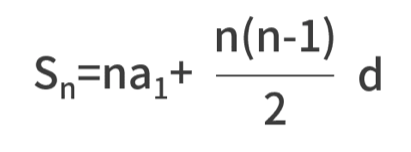
其中 a1 為首項,n 為項數(shù),d 為公差,前 n 項和為 Sn。
利用這個公式,我們可以直接寫出下面的代碼:
import sysn = int(sys.argv[1])a1 = 0d = 2nn = n/2 + 1print nn * a1 + 2 * nn * (nn - 1) / d
獲得輸入變量 n。
求和的第一項,直接賦值為?0。
公差 d 為 2。
第 6 行,求項數(shù)。例如,輸入 6,則項數(shù)為 6/3+1=4 項;輸入 5,則項數(shù)為 5/2+1=3 項。
調(diào)用等差數(shù)列求和公式,直接得到結(jié)果,運行截圖如下:

這段代碼的執(zhí)行與輸入數(shù)據(jù)量 n 毫無關(guān)系,因此復(fù)雜度是 O(1)。
同樣的道理,等比數(shù)列求和的代碼,如果用計算機程序開發(fā)的思想,是需要一個 for 循環(huán)在 O(n)?復(fù)雜度下完成計算的。但借助等比數(shù)列求和公式,你只需要 O(1)?的復(fù)雜度就能得到結(jié)果。
小結(jié)
復(fù)雜度是程序開發(fā)中老生常談的話題了。如果你的數(shù)學(xué)知識非常淵博,從數(shù)學(xué)的角度來降低代碼復(fù)雜度也是一個不錯的選擇。
最后,可以練習(xí)一下:
輸入一個正整數(shù) n,求不大于 n 的所有 2 的正整數(shù)次冪的數(shù)字之和。例如,輸入 17,則輸出 1+2+4+8+16=31;輸入 8,則輸出 1+2+4+8=15。
你可以嘗試兩種方法來開發(fā),分別是 O(n)?復(fù)雜度的 for 循環(huán),和 O(1)?復(fù)雜度的等比數(shù)列求和公式。
推薦閱讀:
技術(shù)人年度總結(jié) | 2020,注定不平凡
前端人因為 Vue3 的 Ref-sugar 提案打起來了!
點點“贊”和“在看”,保護頭發(fā),減少bug。
