你真的了解數(shù)學(xué)中的概率嗎?
概率和統(tǒng)計(jì)學(xué)的關(guān)系十分密切,大量統(tǒng)計(jì)學(xué)的知識(shí)都起源于概率論,現(xiàn)在我們來把它濃縮成一篇文章,當(dāng)然如果想要更深入地學(xué)習(xí),還是建議大家自己看書喲。
概率的本質(zhì)是什么?
我們都知道扔一枚硬幣,正面朝上的概率為0.5,那0.5是什么意思呢?
對(duì)概率的解釋有兩大學(xué)派,主觀概率派和客觀概率派,由兩種解釋建立起了貝葉斯統(tǒng)計(jì)學(xué)和傳統(tǒng)數(shù)理統(tǒng)計(jì)學(xué)(頻率論學(xué)派)。
客觀概率派
客觀概率派中對(duì)概率的解釋是基于物理世界本身存在的隨機(jī)性,客觀概率派中的頻率派,即將頻率作為概率,也就是說要做大量重復(fù)的試驗(yàn)來得到結(jié)論。
還是扔硬幣的問題,正面朝上的概率為0.5,用頻率派的說法就是,如果我們?nèi)缘拇螖?shù)足夠多,那么有大概一半的情況會(huì)出現(xiàn)正面朝上。
我們后面要說的常見名詞中對(duì)于概率的解釋其實(shí)就是客觀概率的說法。
主觀概率派
又叫做貝葉斯派,強(qiáng)調(diào)信念的強(qiáng)度,是我們由于信息不足而對(duì)事件發(fā)生可能性的度量,因?yàn)橛行┦录o法做大量重復(fù)的試驗(yàn),如明天是否會(huì)下雨,只能通過已有信息和邏輯進(jìn)行推斷。
如果我們相信這件事情一定會(huì)發(fā)生,那么它的概率就是1,如果我們不確定這件事情是否發(fā)生,那么它的概率就介于0到1之間。
概率中的幾個(gè)名詞
來說幾個(gè)名詞及相應(yīng)解釋:
試驗(yàn):對(duì)某事物或現(xiàn)象進(jìn)行觀察或?qū)嶒?yàn)
事件:試驗(yàn)的結(jié)果,換句話說,事件可以是任何事情
比如擲骰子,這是一個(gè)試驗(yàn),而擲骰子這個(gè)過程中出現(xiàn)的點(diǎn)數(shù)為1這個(gè)結(jié)果是一個(gè)事件。
隨機(jī)事件:可能出現(xiàn)也可能不出現(xiàn)的事件
必然事件:一定會(huì)出現(xiàn)的事件
不可能事件:一定不會(huì)出現(xiàn)的事件
擲骰子點(diǎn)數(shù)小于7這就是一個(gè)必然事件,點(diǎn)數(shù)大于6就是一個(gè)不可能事件,點(diǎn)數(shù)為奇數(shù)則是一個(gè)隨機(jī)事件
概率:一個(gè)事件在試驗(yàn)中出現(xiàn)的可能性大小的度量,通常用P來表示,其范圍在0~1之間,如P(A)的意思就是發(fā)生事件A的概率。

對(duì)立事件:A事件的對(duì)立事件為A',A'包含A所不包含的一切
互斥事件:如果兩個(gè)事件是互斥事件,意味著他們倆只有一個(gè)會(huì)發(fā)生
相交事件:如果兩個(gè)事件相交,說明它們倆可能同時(shí)發(fā)生
概率除了用公式計(jì)算外,還可以用維恩圖的形式來表示。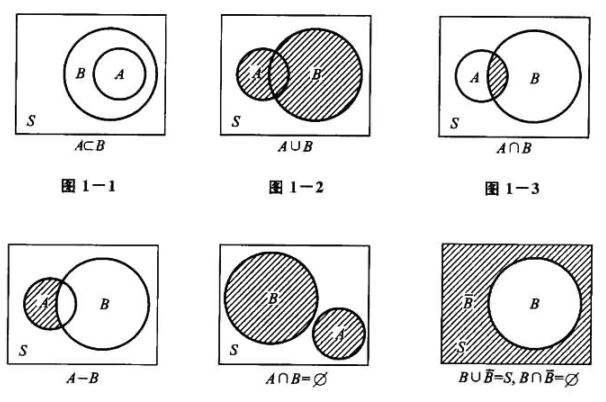
要注意的是,概率只是對(duì)事件發(fā)生可能性的一種表達(dá),絕非擔(dān)保。
條件概率:已知B事件發(fā)生的前提下A事件發(fā)生的概率,用P(A | B)表示,條件概率可用以下公式求解。
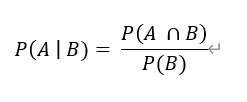
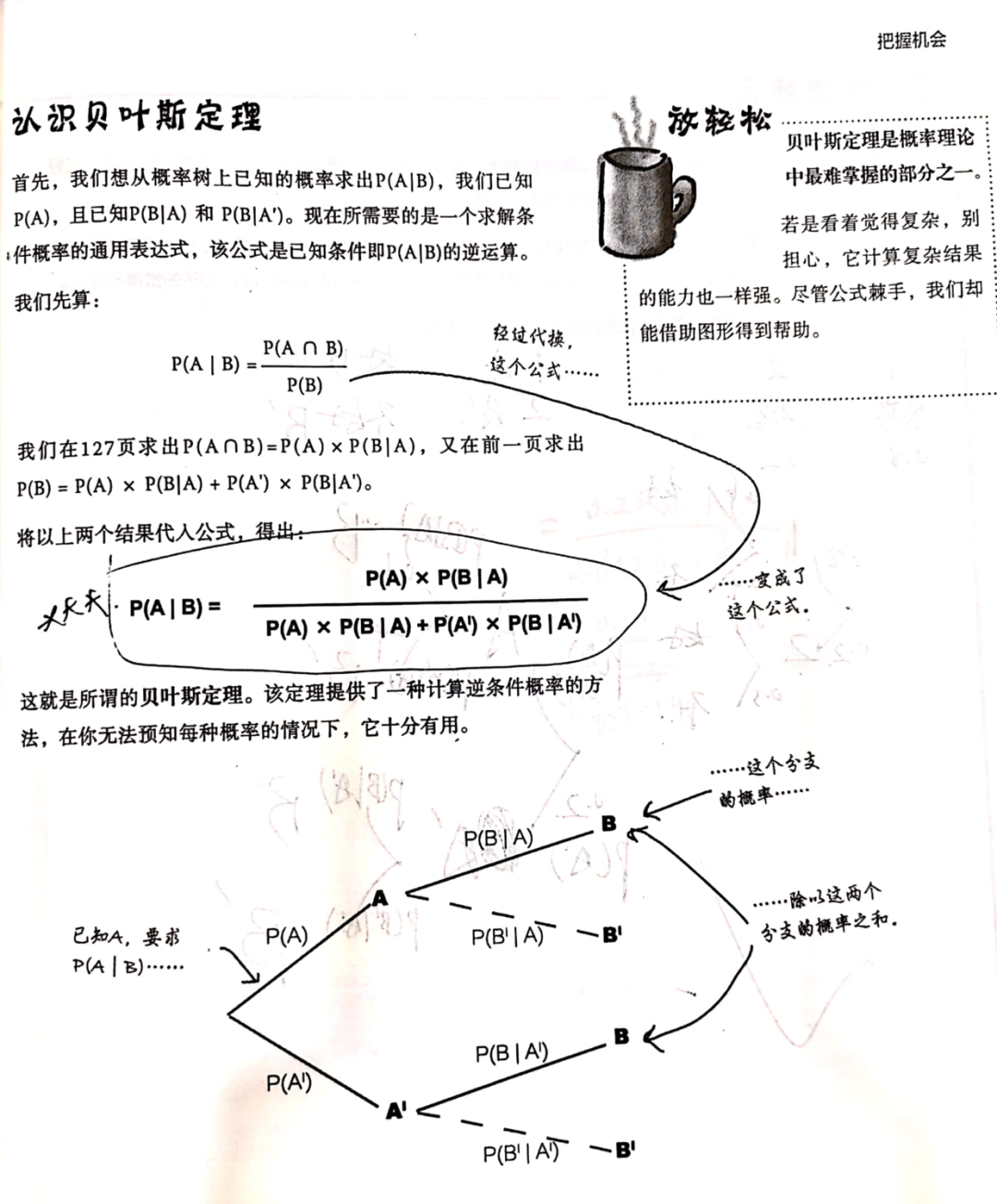
貝葉斯定理:提供了一種計(jì)算逆條件概率的方法,也就是需要求條件概率,但該條件概率與已知條件概率順序相反時(shí)要用到貝葉斯定理。
關(guān)于貝葉斯定理,里面還有全概率公式、先驗(yàn)概率、后驗(yàn)概率等概念的理解,這部分內(nèi)容在《深入淺出統(tǒng)計(jì)學(xué)》里講解的非常好,不單單是窮舉公式,大家可以看下。
相關(guān)事件:如果幾個(gè)事件互有影響,則為相關(guān)事件。
比如從抽屜里拿襪子,直到找出一雙,這是相關(guān)事件,因?yàn)樵谌〕鲆恢灰m子后,受這一動(dòng)作的影響,下一次再取襪子時(shí),襪子的總數(shù)已經(jīng)減少了,會(huì)影響到每一次取襪子的概率,求相關(guān)事件的概率就是求條件概率。
獨(dú)立事件:如果幾個(gè)事件互不影響,就是獨(dú)立事件。還是取襪子,如果取了以后再放回,這就是獨(dú)立事件,因?yàn)榉呕匾院罂倲?shù)不變了,第二次取襪子不會(huì)因?yàn)榈谝淮稳∫m子而受到影響。
離散型隨機(jī)變量的概率分布
概率可以用來衡量一些事件發(fā)生可能性的大小,但它絕非擔(dān)保,如何利用概率預(yù)測(cè)長(zhǎng)期結(jié)果,答案是善用期望,說到期望,就要有概率分布,還是要先熟悉幾個(gè)名詞:
隨機(jī)變量:一個(gè)隨機(jī)事件的所有可能值X,且每個(gè)可能值X都有確定的概率P,X就是P(X)的隨機(jī)變量,P(X)就是X的概率函數(shù)。
離散型隨機(jī)變量:隨機(jī)變量X都能被一一列舉出來,也就是只能取確定的數(shù)值,就是離散型隨機(jī)變量,如一批產(chǎn)品中次品的數(shù)量。
連續(xù)型隨機(jī)變量:隨機(jī)變量X不能被一一列舉出來,如一批電子元器件的壽命。
概率分布:概率分布就是把一個(gè)事件可能發(fā)生的所有概率匯總起來。
篇幅限制,這一節(jié)就先寫到離散型隨機(jī)變量的概率分布,下節(jié)再寫連續(xù)型隨機(jī)變量的概率分布。
離散型隨機(jī)變量的期望和方差
期望:就是離散型隨機(jī)變量X的各個(gè)值與其概率乘積的和,通常表示為E(X),期望指示了預(yù)測(cè)的結(jié)果。
方差:是每個(gè)隨機(jī)變量與其期望值的離差平方的期望值,用VAR(X)表示,方差表示了結(jié)果的分散性。
概率分布的期望和方差也有一些比較重要的線性變換的性質(zhì),比如: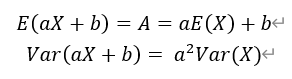
線性
當(dāng)每個(gè)事件相互獨(dú)立時(shí),期望和方差的計(jì)算則按以下公式: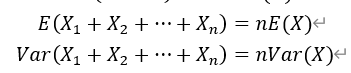
獨(dú)立
