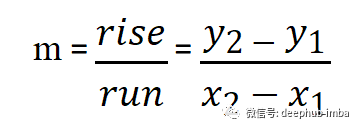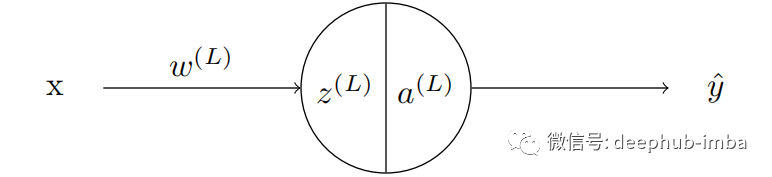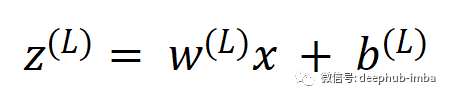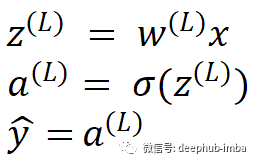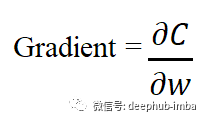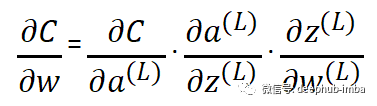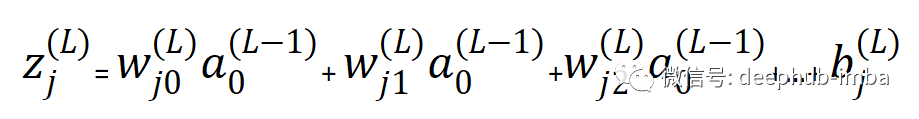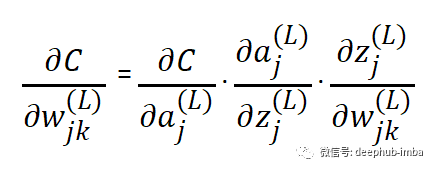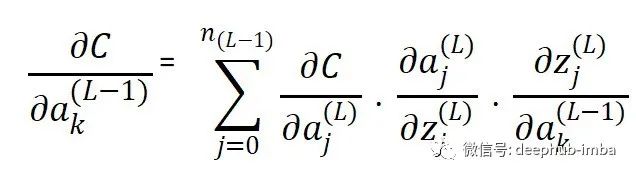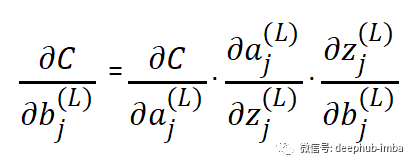清華大數(shù)據(jù)軟件團(tuán)隊官方微信公眾號
來源：Deephub Imba
本文約3500字，建議閱讀5分鐘?
如何計算隱藏層中的誤差?微積分和這些有什么關(guān)系?

反向傳播是神經(jīng)網(wǎng)絡(luò)通過調(diào)整神經(jīng)元的權(quán)重和偏差來最小化其預(yù)測輸出誤差的過程。但是這些變化是如何發(fā)生的呢?如何計算隱藏層中的誤差?微積分和這些有什么關(guān)系?在本文中，你將得到所有問題的回答。讓我們開始吧。

在了解反向傳播的細(xì)節(jié)之前，讓我們先瀏覽一下整個神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)過程：

神經(jīng)網(wǎng)絡(luò)是如何進(jìn)行學(xué)習(xí)的？

神經(jīng)網(wǎng)絡(luò)中的學(xué)習(xí)過程分為三個步驟。

第 1 步：將數(shù)據(jù)輸入神經(jīng)網(wǎng)絡(luò)。該輸入數(shù)據(jù)順序通過神經(jīng)網(wǎng)絡(luò)的不同層，并在最終輸出層產(chǎn)生輸出或預(yù)測。數(shù)據(jù)從輸入層流向輸出層的整個過程稱為前向傳播。我們將在下面看到前向傳播的細(xì)節(jié)。

第 2 步：現(xiàn)在有了輸出，我們計算輸出中的損失。我們有很多計算損失的選項，例如均方誤差、二元交叉熵等，如何計算損失是根據(jù)不同的目標(biāo)來定義的。

第 3 步：計算損失后，我們必須告訴神經(jīng)網(wǎng)絡(luò)如何改變它的參數(shù)（權(quán)重和偏差）以最小化損失。這個過程稱為反向傳播。

神經(jīng)網(wǎng)絡(luò)中的前向傳播

NN 基本上由三種類型的層組成。輸入層、隱藏層和輸出層。通過 NN 的數(shù)據(jù)流是這樣的：

• 數(shù)據(jù)第一次在網(wǎng)絡(luò)中向前流動時，將需要訓(xùn)練神經(jīng)網(wǎng)絡(luò)的輸入或特征輸入到輸入層的神經(jīng)元中。
• 然后這些輸入值通過隱藏層的神經(jīng)元，首先乘以神經(jīng)元中的權(quán)重，然后加上一個偏差。我們可以稱之為預(yù)激活函數(shù)。
• 預(yù)激活函數(shù)之后就是激活函數(shù)。有很多激活函數(shù)，例如 sigmoid、tanh、relu 等，激活函數(shù)的作用是加入非線性的因素。
• 最后一層是輸出層，其中顯示了神經(jīng)網(wǎng)絡(luò)的計算輸出。

損失函數(shù)

當(dāng)輸入通過向前傳播產(chǎn)生輸出后，我們可以在輸出中找出誤差。誤差是預(yù)測輸出和期望的真實值之間的差異。但在神經(jīng)網(wǎng)絡(luò)中通常不計算輸出中的誤差，而是使用特定的損失函數(shù)來計算損失，并隨后在優(yōu)化算法中使用該函數(shù)來將損失降低到最小值。

計算損失的方法有很多，如均方誤差、二元交叉熵等。這些使用那個損失是根據(jù)我們要解決的問題來選擇的。

梯度下降算法

反向傳播的全部思想是最小化損失。我們有很多優(yōu)化算法來做到這一點。但為了簡單起見，讓我們從一個基本但強(qiáng)大的優(yōu)化算法開始，梯度下降算法。

這里的想法是計算相對于每個參數(shù)的損失變化率，并在減少損失的方向上修改每個參數(shù)。任何參數(shù)的變化都會導(dǎo)致?lián)p失發(fā)生改變。如果變化為負(fù)，那么我們需要增加權(quán)重以減少損失，而如果變化為正，我們需要減少權(quán)重。我們可以用數(shù)學(xué)方式將其寫為，

new_weight = old_weight - learning_rate * gradient

其中梯度是損失函數(shù)相對于權(quán)重的偏導(dǎo)數(shù)。學(xué)習(xí)率只是一個縮放因子，用于放大或縮小梯度。在接下來的文本中更詳細(xì)地解釋了它。相同的公式適用于偏差：

new_bias = old_bias - learning_rate * gradient

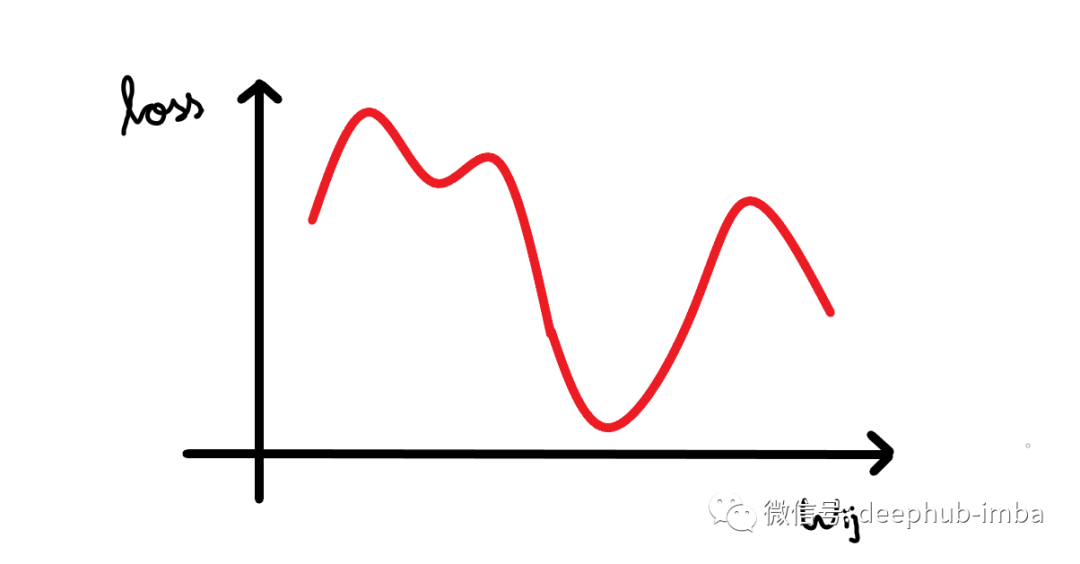
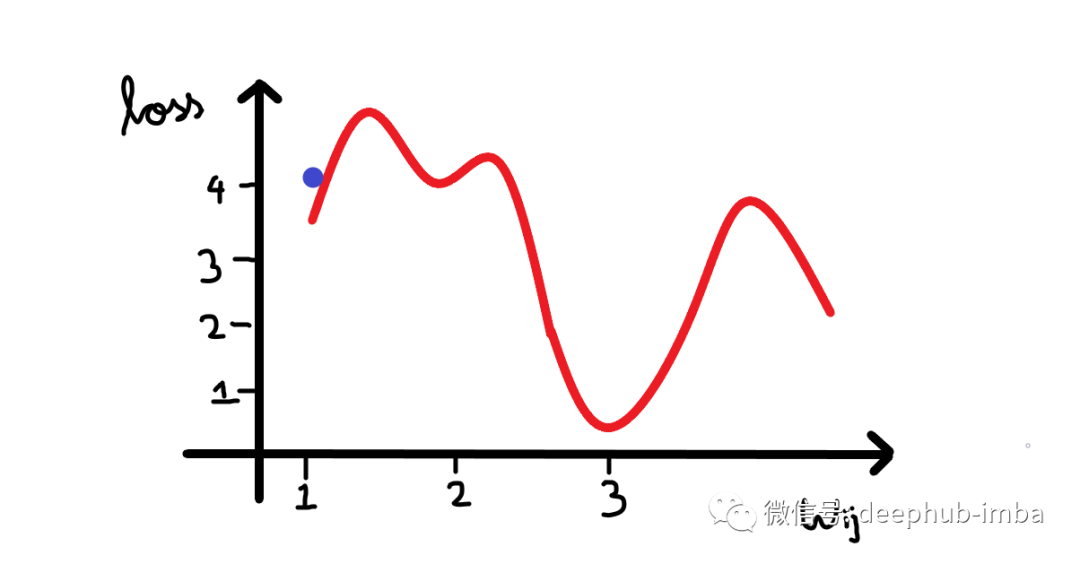
其中梯度是損失函數(shù)相對于偏差的偏導(dǎo)數(shù)。

看看下面的圖表。我們繪制了神經(jīng)網(wǎng)絡(luò)的損失與單個神經(jīng)元權(quán)重變化的關(guān)系圖。

現(xiàn)在我們可以看到曲線中有很多局部最小值（所有下凹曲線），但我們感興趣的是將損失降低到全局最小值（最大的下凹曲線）。假設(shè)我們的權(quán)重值現(xiàn)在接近示例圖中的原點（假設(shè)為 1，因此我們的損失接近 4）。

在上圖中權(quán)重值約為3的時候損失最小。

所以我們的算法必須能夠找到這個權(quán)重值（3），來使得損失最小。所以權(quán)重的改變應(yīng)該與損失成某個比例。這就是為什么梯度是由損失相對于權(quán)重的偏導(dǎo)數(shù)給出的。所以梯度下降算法的步驟是：

• 計算梯度(損失函數(shù)相對于權(quán)重/偏差的偏導(dǎo)數(shù))
• 梯度乘以學(xué)習(xí)速率。
• 然后從權(quán)重/偏差中減去梯度乘以學(xué)習(xí)速率。

對以上操作進(jìn)行迭代，直到損失收斂到全局最小值。

關(guān)于梯度的更多信息

由于直線的斜率可以使用通用斜率公式計算：

取直線上相距一定距離的兩點，計算斜率。當(dāng)圖形是一條直線時，這種計算梯度的方法給出了精確的計算。但是當(dāng)我們有不均勻的曲線時，使用這種方式計算梯度一個好主意。因為這些圖中的每個點的損失都在不斷變化，尤其是當(dāng)曲線不規(guī)則時，如果我們可以使我們計算斜率的鄰域或距離無限小呢？這樣不就可以計算最準(zhǔn)確的梯度值了嗎？

對，這正是通過計算 y 相對于 x 的導(dǎo)數(shù)所做的。這為我們提供了 y 相對于 x 的瞬時變化率。瞬時變化率為我們提供了比我們之前的運行遞增法方更精確的梯度，因為這個梯度是瞬時的。在計算相對于權(quán)重或偏差的損失變化率時，應(yīng)遵循相同的方法。損失函數(shù)相對于權(quán)重的導(dǎo)數(shù)為我們提供了損失相對于權(quán)重的瞬時變化率。

學(xué)習(xí)率

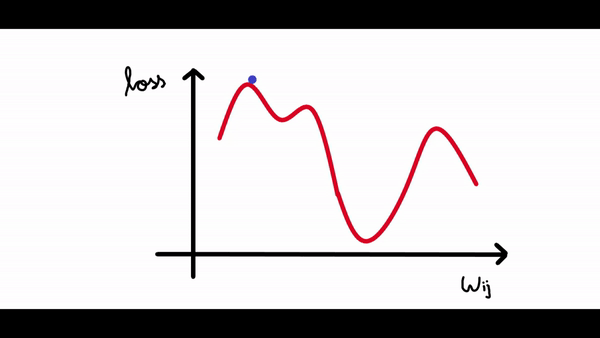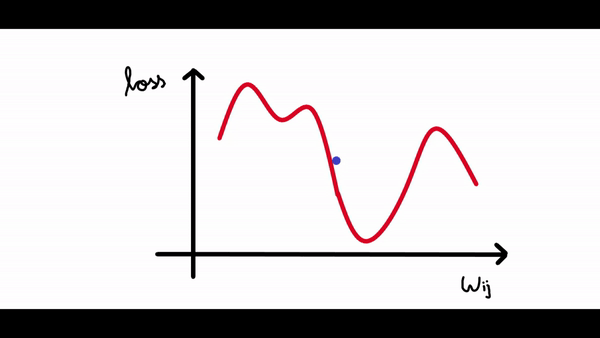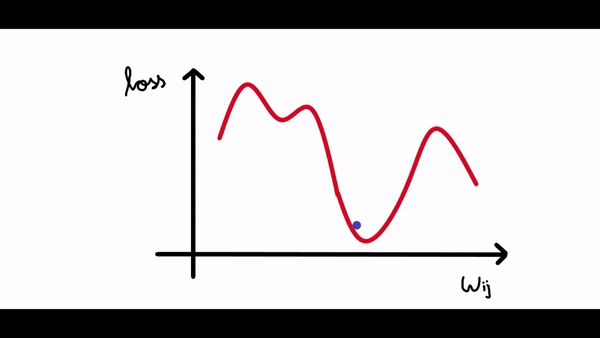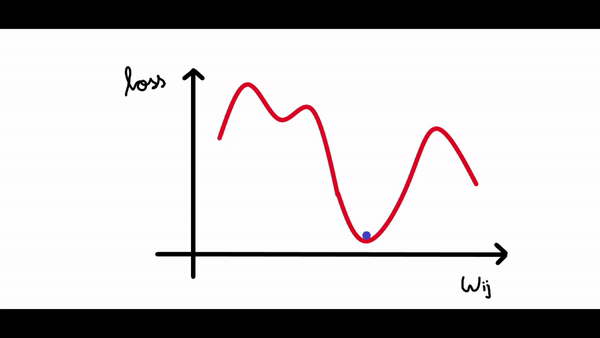
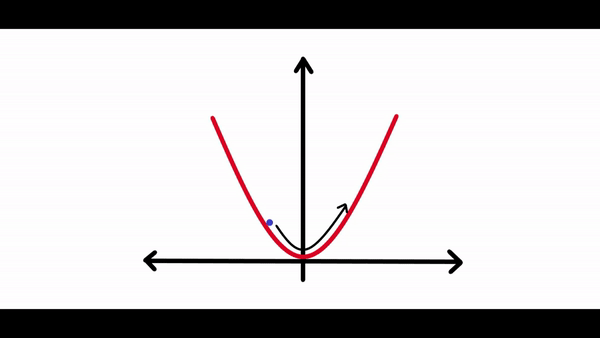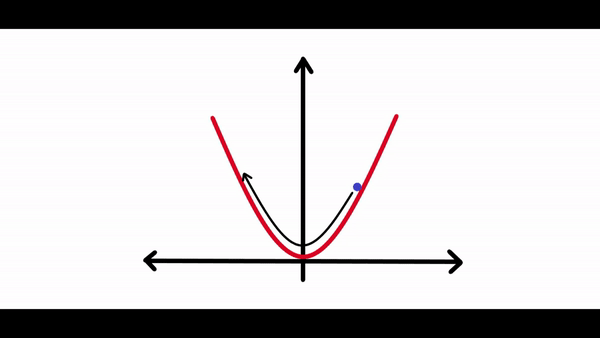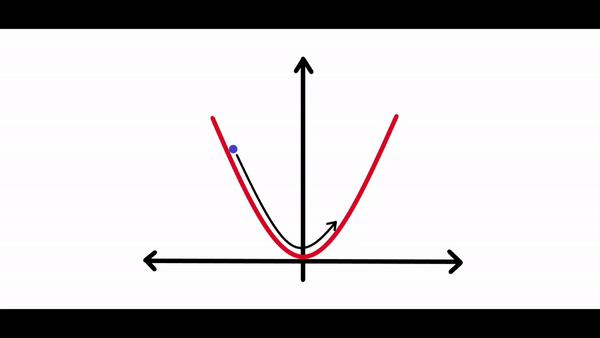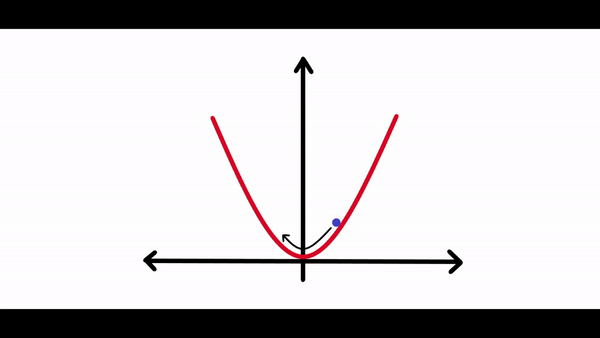
在計算完梯度之后需要一些東西來縮放梯度。因為有時候神經(jīng)網(wǎng)絡(luò)試圖朝著損耗曲線的最低點前進(jìn)時，它可能會在每次調(diào)整其權(quán)重時采取很大的調(diào)整，調(diào)整過大可能永遠(yuǎn)不會真正收斂到全局最小值。你可以在下面的圖表中看到：

正如你所看到的，損失會持續(xù)朝任何方向移動，并且永遠(yuǎn)不會真正收斂到最小值。如果學(xué)習(xí)速度太小，損失可能需要數(shù)年的時間才能收斂到最小。因此最佳學(xué)習(xí)率對于任何神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)都是至關(guān)重要的。

因此，每次參數(shù)更新時，我們使用學(xué)習(xí)速率來控制梯度的大小。讓我重申一下上面看到的更新參數(shù)的公式。

new_weight = old_weight - learning_rate * gradient

所以學(xué)習(xí)速率決定了每一步的大小同時收斂到最小值。

計算梯度

計算的損失是由于網(wǎng)絡(luò)中所有神經(jīng)元的權(quán)重和偏差造成的。有些權(quán)重可能比其他權(quán)重對輸出的影響更大，而有些權(quán)重可能根本沒有影響輸出。

前面已經(jīng)說了我們訓(xùn)練的目標(biāo)是減少輸出中的誤差。要做到這一點必須計算每個神經(jīng)元的梯度。然后將這個梯度與學(xué)習(xí)速率相乘，并從當(dāng)前的權(quán)重(或偏差)中減去這個值。這種調(diào)整發(fā)生在網(wǎng)絡(luò)中的每一個神經(jīng)元中。現(xiàn)在讓我們考慮只有一個神經(jīng)元的神經(jīng)網(wǎng)絡(luò)。

• L-層數(shù)
• w-權(quán)重
• z- 預(yù)激活函數(shù)
• a- 激活函數(shù)
• y-輸出

預(yù)激活 z 可以寫為，

為了簡單起見，讓我們暫時忽略偏差b。

然后 z 的值由激活函數(shù)激活。這個例子中我們使用 sigmoid 激活函數(shù)。sigmoid 激活函數(shù)由符號 σ 表示。

這個網(wǎng)絡(luò)的輸出是 y-hat。通過使用可用的各種損失函數(shù)之一來完成計算損失。讓我們用字母 C 表示損失函數(shù)。現(xiàn)在該進(jìn)行反向傳播了，計算損失函數(shù)的梯度：

這個值告訴我們權(quán)重的任何變化如何影響損失。

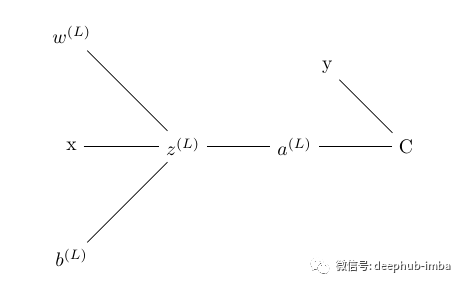
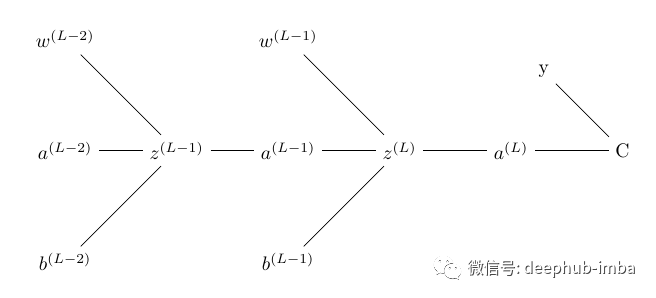
為了計算梯度，我們使用鏈?zhǔn)椒▌t來尋找導(dǎo)數(shù)。我們使用鏈?zhǔn)椒▌t是因為誤差不受權(quán)重的直接影響， 權(quán)重影響預(yù)激活函數(shù)，進(jìn)而影響激活函數(shù)，進(jìn)而影響輸出，最后影響損失。下面的樹顯示了每個術(shù)語如何依賴于上面網(wǎng)絡(luò)中的另一個術(shù)語。

預(yù)激活函數(shù)取決于輸入、權(quán)重和偏差、激活函數(shù)依賴于預(yù)激活函數(shù)、損失取決于激活函數(shù)

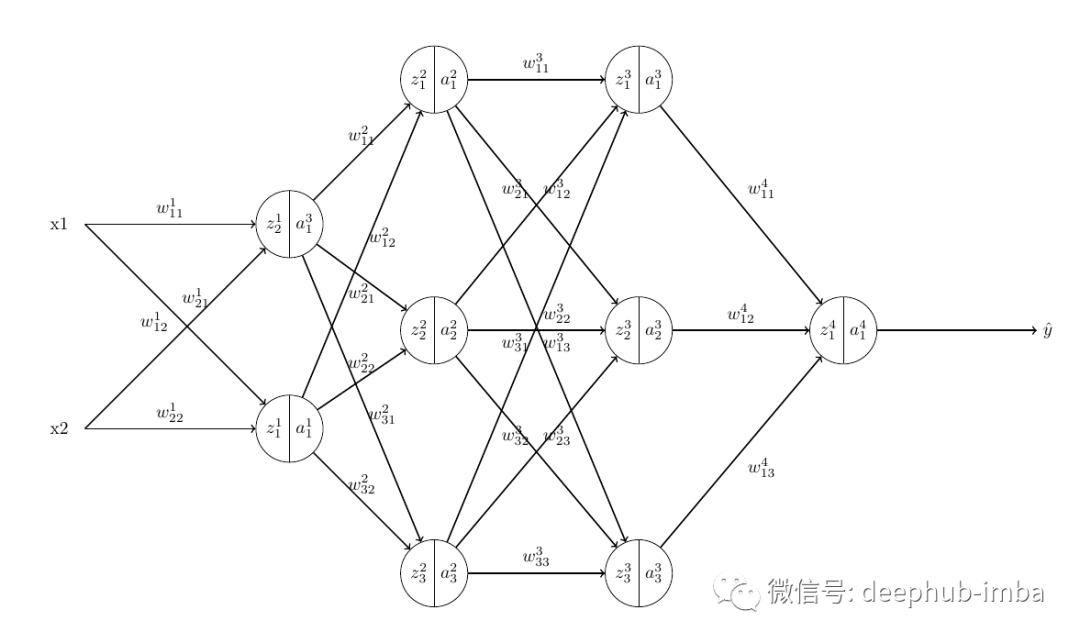
圖像右上角的 y 是與預(yù)測輸出進(jìn)行比較并計算損失的真實值。

所以當(dāng)我們應(yīng)用鏈?zhǔn)椒▌t時，我們得到：

我們有另一個詞來指代這個梯度，即損失相對于權(quán)重的瞬時變化率。將這些從單個神經(jīng)元網(wǎng)絡(luò)的梯度計算中獲得的知識外推到具有四層的真正神經(jīng)網(wǎng)絡(luò)：一個輸入層、兩個隱藏層和一個輸出層。

每個神經(jīng)元的預(yù)激活函數(shù)由下式給出

• L-層數(shù)
• j- 計算預(yù)激活函數(shù)的神經(jīng)元的索引
• z- 預(yù)激活函數(shù)
• w-神經(jīng)元的權(quán)重
• a- 前一個神經(jīng)元的激活輸出

除了我們沒有激活函數(shù)的輸入層之外的所有神經(jīng)元都是如此。因為在輸入層中z 只是輸入與其權(quán)重相乘的總和（不是前一個神經(jīng)元的激活輸出）。

這里的梯度由下式給出，

其中 w 是分別連接 L-1 層和 L 層節(jié)點 k 和 j 的權(quán)重。k 是前一個節(jié)點，j 是后繼節(jié)點。但是這可能會引發(fā)一個新的問題：為什么是wjk而不是wkj呢？這只是在使用矩陣將權(quán)重與輸入相乘時要遵循的命名約定。（所以暫時先不管他）

下面的樹可以看到它們之間相互依賴

可以看到，前一層節(jié)點的激活函數(shù)的輸出作為后一層節(jié)點的輸入。如果知道以下項的值，就可以輕松計算輸出節(jié)點中的梯度：

• 誤差對激活函數(shù)的導(dǎo)數(shù)
• 激活函數(shù)相對于預(yù)激活函數(shù)的導(dǎo)數(shù)
• 預(yù)激活函數(shù)相對于權(quán)重的導(dǎo)數(shù)。

但是當(dāng)我們在隱藏層計算梯度時，我們必須單獨計算損失函數(shù)相對于激活函數(shù)的導(dǎo)數(shù)，然后才能在上面的公式中使用它。

這個方程與第一個方程幾乎相同（損失函數(shù)相對于權(quán)重的推導(dǎo)）。但在這里有一個總結(jié)。這是因為與權(quán)重不同，一個神經(jīng)元的激活函數(shù)可以影響它所連接的下一層中所有神經(jīng)元的結(jié)果。

需要說明的是 ：這里沒有編寫用于推導(dǎo)與輸出層中的激活函數(shù)相關(guān)的損失函數(shù)的鏈?zhǔn)椒▌t的單獨方程。那是因為輸出層的激活函數(shù)直接影響誤差。但隱藏層和輸入層的激活函數(shù)并非如此。它們通過網(wǎng)絡(luò)中的不同路徑間接影響最終輸出。

通過以上的計算，在計算網(wǎng)絡(luò)中所有節(jié)點的梯度后，乘以學(xué)習(xí)率并從相應(yīng)的權(quán)重中減去。

這就是反向傳播和權(quán)重調(diào)整的方式。經(jīng)過多次迭代這個過程，將損失減少到全局最小值，最終訓(xùn)練結(jié)束。

還差一個偏差

偏差也以與重量相同的方式經(jīng)歷一切！

與權(quán)重一樣，偏差也會影響網(wǎng)絡(luò)的輸出。因此在每次訓(xùn)練迭代中，當(dāng)針對權(quán)重的損失計算梯度時，同時計算相對于偏差的損失的梯度。

對于隱藏層，損失函數(shù)相對于前一層激活函數(shù)的推導(dǎo)也將使用鏈?zhǔn)椒▌t單獨計算。因此梯度被反向傳播并且每個節(jié)點的偏差被調(diào)整。

總結(jié)

當(dāng)損失被反向傳播和最小化時，這就是在每個訓(xùn)練循環(huán)期間發(fā)生的所有事情。我希望這篇文章已經(jīng)消除了數(shù)學(xué)中的晦澀難懂的概念，并使用了一種簡單的方式將整個反向傳播的過程描述清楚了。如果你有什么建議，歡迎留言。

編輯：王菁

校對：林亦霖