免费看黄色片视频,中文字幕久久青青,手机看片福利一区,国产成人精品三级麻豆,高清无码在线视频网站,男女啪啪的网站,草草在线观看,日韩无码电影免费

學(xué)習(xí)里經(jīng)常出現(xiàn)張量（Tensor），這個(gè)概念說平常也很平常，但它背后涉及的數(shù)學(xué)并不算淺顯。

張量這個(gè)詞在不同領(lǐng)域的人看來貌似有點(diǎn)一詞多意。一般來說，你只要知道張量是一個(gè)多維數(shù)組，差不多也就夠了。比如著名的 Tensorflow 里的這個(gè) tensor。

但如果真要掌握和應(yīng)用相關(guān)的數(shù)學(xué)理論，那非得了解更多不可。1

張量小史

先來一碟開胃菜，大概了解下這個(gè)詞以及相關(guān)理論的發(fā)展歷程。

這里主要羅列相關(guān)概念的提出者及年代，而它們之間的傳承關(guān)系由于缺乏引文不一定可考。歷史真相的來龍去脈有時(shí)候只能憑大家遐想了。

1、先看張量積這個(gè)概念。大概 1884 年左右，美國(guó)物理學(xué)家 Gibbs（吉布斯）引入了中向量的張量積這個(gè)概念（他當(dāng)時(shí)命名為 indeterminante product），后來他將其推廣到維。

Gibbs 這樣命名的原因是他認(rèn)為這個(gè)乘積是兩個(gè)向量乘積的最一般形式，它只需要滿足作為積（product）的基本定律，即所謂的雙線性，而不需要考慮其他任何定律，也因此具有很大不確定性。個(gè)人感覺 Gibbs 這點(diǎn)為張量的現(xiàn)代版數(shù)學(xué)定義奠定了基礎(chǔ)。

2、德國(guó)物理學(xué)家 Voigt（福格特）于 1898 年使用張量來描述晶體上的應(yīng)力和應(yīng)變，這就是具有現(xiàn)代意義的張量這個(gè)詞的首次出現(xiàn)。

3、意大利數(shù)學(xué)家 Ricci（里奇）在 1880-1890 年間將張量應(yīng)用于微分幾何，整出了所謂的絕對(duì)微積分。隨后，Ricci 與學(xué)生 Levi-Civita (列維-奇維塔) 共同構(gòu)建了張量分析，為愛因斯坦的廣義相對(duì)論奠定了理論基礎(chǔ)。張量一詞在物理學(xué)和數(shù)學(xué)中得到廣泛使用可能部分歸功于愛因斯坦。

4、至此，張量積是由向量空間構(gòu)建的。二十世紀(jì)，有人將張量積擴(kuò)展到模（module）。

說了這么多，也沒有看到張量到底是個(gè)什么東西？是吧，說明這個(gè)詞不是一兩句話就能解釋清楚了。但這里大家可以看到，張量似乎離不開張量積。

張量的定義

我們來看看現(xiàn)代版的定義，翻一下數(shù)學(xué)書，或者看下 wikipedia，發(fā)現(xiàn)是下面這樣子的。

Given a finite set of vector spaces over a common field one may form their tensor product an element of which is termed a tensor. A tensor on the vector space is then defined to be an element of (i.e., a vector in) a vector space of the form:

V \otimes \cdots \otimes V \otimes V^{\star} \otimes \cdots \otimes V^{\star}

where is the dual space of .

If there are copies of and copies of in our product, the tensor is said to be of type and contravariant of order and covariant order and total order . The tensors of order zero are just the scalars (elements of the field , those of contravariant order 1 are the vectors in and those of covariant order 1 are the one-forms in (for this reason the last two spaces are often called the contravariant and covariant vectors). The space of all tensors of type is denoted

T_{n}^{m}(V)=\underbrace{V \otimes \cdots \otimes V}_{m} \otimes \underbrace{V^{\star} \otimes \cdots \otimes V^{\star}}_{n}.

這里光定義，就有線性（向量）空間、張量積、對(duì)偶空間、協(xié)變、逆變等概念，初次看到的同學(xué)可能一頭霧水。

我們?cè)賮砜匆粋€(gè)形式上更簡(jiǎn)練一點(diǎn)的，

定義設(shè) 為向量空間的對(duì)偶空間，稱重線性函數(shù)，

\mathcal{F}: \overbrace{V^{\star} \times \cdots \times V^{\star}}^{m 個(gè)} \times \overbrace{V \times \cdots \times V}^{n 個(gè)} \rightarrow R

為向量空間上的型張量（tensor)。

并將向量空間上的所有型張量構(gòu)成的集合記為:

L(\overbrace{V^{\star}, \cdots, V^{\star}}^{m 個(gè)}, \overbrace{V, \cdots, V}^{n 個(gè)} ; R)

原來在數(shù)學(xué)家眼里，張量就是一個(gè)多重（chong，二聲）線性函數(shù)啊。

那么，這個(gè)函數(shù)的輸入輸出分別是什么呢？看定義，輸入是對(duì)偶空間里的個(gè)向量以及向量空間里的個(gè)向量，而輸出就是一個(gè)實(shí)數(shù)，這里的個(gè)數(shù)可以是 0。

這樣說貌似比較數(shù)學(xué)，工科同學(xué)或許得去補(bǔ)一些功課。咱先別管對(duì)偶空間啥的，今天我們想通過一個(gè)比較簡(jiǎn)單的例子來闡述一下張量這個(gè)概念。

下面正式開始我們的故事。3

躺平也能搞事情

在試圖理解張量之前，我們先了解一下兩個(gè)概念，即逆變和協(xié)變。它們描述了幾何上或物理中的某些量是如何隨著基的改變而規(guī)律地改變的。

等等，這些跟躺平有啥關(guān)系呢？看了半天沒看到實(shí)質(zhì)內(nèi)容啊，太標(biāo)題黨了吧。

表急，我們來看一個(gè)式子，

[u, v] \begin{bmatrix} x \\ y \end{bmatrix} = ux + vy

上面四個(gè)數(shù)都來自實(shí)數(shù)域。

這時(shí)，有個(gè)叫小明的同學(xué)舉手了，問：老師，這不是兩個(gè)向量搞內(nèi)卷嗎？哦不，搞內(nèi)積嗎？

老師：可以這么看。但是注意，這里我們并不把這個(gè)運(yùn)算當(dāng)作向量的內(nèi)積，而是兩個(gè)來自不同星星（空間）的同學(xué)（向量）一起搞事情。

為了形象一些，你也可以把上式看成一個(gè)行向量和一個(gè)列向量作了某種運(yùn)算。總之，它倆一結(jié)合，變出來一個(gè)實(shí)數(shù)。

注意看，它們中一個(gè)是躺著的，一個(gè)是站著的，姿勢(shì)是不同的。

其實(shí)它們對(duì)應(yīng)著不同的張量。那么到底怎么個(gè)不同呢？

我們來打個(gè)比方，假設(shè)它們對(duì)應(yīng)兩類青年，一類躺平青年，一類上進(jìn)青年。（躺平的反面是上進(jìn)嗎？我不知道，這里咱們姑且這么說吧）。

但是這里想說的是，躺平并不代表不干活，甚至不能說不上進(jìn)，而僅僅是干活的姿態(tài)不同而已。

言歸正傳，上面兩個(gè)不同張量怎么干活呢？這里所謂的干活就是給它輸入某些東西，它出來另外一些東西。用數(shù)學(xué)概念來說就是一個(gè)映射，因?yàn)檫@里最后出來的是一個(gè)數(shù)，所以是一個(gè)函數(shù)。

先看躺平向量對(duì)應(yīng)的那個(gè)張量的干活姿勢(shì)。我們將這個(gè)躺平向量記為，給它輸入一個(gè)上進(jìn)向量，它們倆深入溝通一番，融為一體，出來一個(gè)數(shù)。對(duì)，就是下面這樣子，

[a, b] \begin{bmatrix} x \\ y \end{bmatrix} = ax + by

不妨改寫一下，變成函數(shù)的樣子，

\mathcal{F}_{[a,b]}\left(\begin{bmatrix} x \\ y \end{bmatrix}\right) = ax + by

這就是給定的某個(gè)躺平向量的干活姿勢(shì)。因?yàn)檫@里是指定的某個(gè)躺平向量，所以上面的和是固定的，而和是可變的。給定一個(gè)躺平向量，它出的活（生的娃）可能差別挺大，就看你給它配的是怎么樣的上進(jìn)向量了。

再啰嗦一下，假設(shè)這里的躺平向量是你自己，那么給你配個(gè)上進(jìn)向量（對(duì)象），你倆就能出活啊。給你不同的對(duì)象，你能出不同活。給你個(gè)女神男神，你出的活好。。。總之，你躺在那里，等著對(duì)象來，無限可能。

好了，該醒過來了。再次看一下上面這個(gè)函數(shù)，發(fā)現(xiàn)它還是個(gè)線性函數(shù)，即滿足

\begin{array}[ccc]{} \mathcal{F}_{[a,b]}\left(\lambda_1 \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} + \lambda_2 \begin{bmatrix} x_2 \\ y_2 \end{bmatrix}\right) = \lambda_1 \mathcal{F}_{[a,b]}\left(\begin{bmatrix} x_1 \\ y_1 \end{bmatrix} \right) + \lambda_2 \mathcal{F}_{[a,b]}\left(\begin{bmatrix} x_2 \\ y_2 \end{bmatrix}\right) \end{array}

不過，這里還忽略一個(gè)事情，那就是你這個(gè)躺平向量的和以及上進(jìn)向量里的和都是些啥東西啊？對(duì)應(yīng)出生嗎？或者天賦、內(nèi)在屬性什么的？我們先不管它們代表什么，只考慮這個(gè)形式。

蕓蕓眾生，皆是螻蟻。

螻蟻是不是很小啊。對(duì)，小到可以忽略大小，就是數(shù)學(xué)中的點(diǎn)，坐標(biāo)點(diǎn)。

既然是坐標(biāo)點(diǎn)，那就得涉及坐標(biāo)系了。

我們先來看上進(jìn)向量的坐標(biāo) ，它是根據(jù)世界坐標(biāo)系（這里是二維的）而言的，即隱藏著一組基。下面，把它們寫出來看看，

{\bf s} = \begin{bmatrix} \color{red}{1} & \color{blue}{0} \\ \color{red}{0} & \color{blue}{1} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = [\color{red}{e_1}, \; \color{blue}{e_2}]\begin{bmatrix} x \\ y \end{bmatrix} = x{e_1} + y {e_2}

換句話說，點(diǎn)的坐標(biāo)對(duì)應(yīng)著背后的坐標(biāo)軸（基向量）。

小明同學(xué)提問：那么當(dāng)基變了以后，點(diǎn)的坐標(biāo)是不是也得變呢？

是的，問題是怎么變呢？好，下面咱們就來摸索下這個(gè)規(guī)律。

已知一個(gè)線性空間的兩組基和（統(tǒng)一看成列向量），我們可以用一個(gè)矩陣來表示它們之間的轉(zhuǎn)換關(guān)系，

[e_{1^{\prime}},e_{2^{\prime}},\cdots , e_{n^{\prime}}]= \left[e_{1},e_{2},\cdots,e_{n}\right] \left[\begin{array}{cccc} a_{1^{\prime}}^{1} & a_{2^{\prime}}^{1} & \cdots & a_{n^{\prime}}^{1} \\ a_{1^{\prime}}^{2} & a_{2^{\prime}}^{2} & \cdots & a_{n^{\prime}}^{2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1^{\prime}}^{n} & a_{2^{\prime}}^{n} & \cdots & a_{n^{\prime}}^{n} \end{array}\right]= \left[e_{1},e_{2},\cdots,e_{n}\right]\boldsymbol{A}

上式可以看成矩陣乘法。如果把基向量單獨(dú)拿出來看，就是。

對(duì)于中向量，有，而其在另一組基下的表示為

u=\sum_{i^{\prime}}u^{i^{\prime}} e_{i^{\prime}}=\sum_{i^{\prime}}u^{i^\prime} \sum_{i} a^{i}_{i^{\prime}}e_{i}=\sum_{i}\color{red}{ \sum_{i^{\prime}}u^{i^\prime} a^{i}_{i^{\prime}}}e_{i}

對(duì)比紅色部分，得。將其寫成矩陣形式:

\left[\begin{array}{c} u^{1} \\ u^{2} \\ \vdots \\ u^{n} \end{array}\right]= \left[\begin{array}{cccc} a_{1^{\prime}}^{1} & a_{2^{\prime}}^{1} & \cdots & a_{n^{\prime}}^{1} \\ a_{1^{\prime}}^{2} & a_{2^{\prime}}^{2} & \cdots & a_{n^{\prime}}^{2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1^{\prime}}^{n} & a_{2^{\prime}}^{n} & \cdots & a_{n^{\prime}}^{n} \end{array}\right] \left[\begin{array}{c} u^{1^{\prime}} \\ u^{2^{\prime}} \\ \vdots \\ u^{n^{\prime}} \end{array}\right]=\boldsymbol{A}\left[\begin{array}{c} u^{1^{\prime}} \\ u^{2^{\prime}} \\ \vdots \\ u^{n^{\prime}} \end{array}\right]

由此可得:

\left[\begin{array}{c} u^{1^{\prime}} \\ u^{2^{\prime}} \\ \vdots \\ u^{n^{\prime}} \end{array}\right]=\boldsymbol{A}^{-1}\left[\begin{array}{c} u^{1} \\ u^{2} \\ \vdots \\ u^{n} \end{array}\right] \qquad (1)

回到我們二維的例子，上進(jìn)向量的老坐標(biāo)為。那么，在新的坐標(biāo)系下坐標(biāo)會(huì)變成什么呢？代入上面式（1），假設(shè)這里基變換矩陣仍然用表示，則有

\left[\begin{array}{c} x^{\prime} \\ y^{\prime} \end{array}\right]=\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right]

為了加深印象，我們來看個(gè)圖。

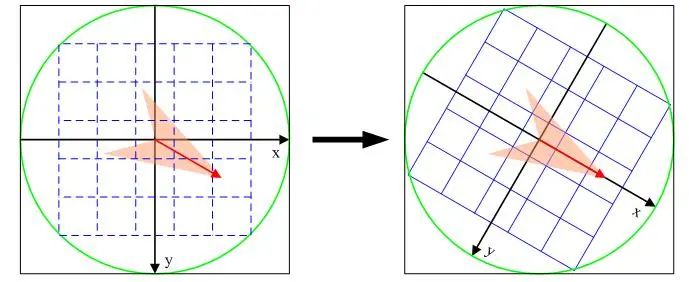
這里假設(shè)坐標(biāo)系之間的變換是旋轉(zhuǎn)，右圖表示將原坐標(biāo)系順時(shí)針旋轉(zhuǎn) 30 度。此時(shí)，紅色那個(gè)向量還是原來的向量，大小和方向都沒變，但它的坐標(biāo)變了。坐標(biāo)是不是變?yōu)?strong>逆時(shí)針旋轉(zhuǎn) 30 度？順時(shí)、逆時(shí)相同度數(shù)，它們對(duì)應(yīng)的矩陣剛好互逆。

還記得你要和它一起搞事情嗎？對(duì)，就是下面這個(gè)

[a, b] \begin{bmatrix} x \\ y \end{bmatrix} = ax + by

但這個(gè)時(shí)候你和它的坐標(biāo)都已經(jīng)變了，要用新的基來表示。具體就是下面這個(gè)樣子了，

[a^{\prime}, b^{\prime}] \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = a^{\prime}x^{\prime} + b^{\prime}y^{\prime}

代入的舊坐標(biāo)，得

[a^{\prime}, b^{\prime}] \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = [a^{\prime}, b^{\prime}] \;\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right]

還記得你們搞出來的數(shù)嗎，就是。觀察一下，如何讓你的新坐標(biāo)代入上式得到相同的結(jié)果呢？其實(shí)很方便，為了讓你能夠與任意上進(jìn)向量保持搞相同事情的能力，你的坐標(biāo)可以變換成下面這個(gè)樣子，

[a^{\prime}, b^{\prime}] = [a, b]\;\boldsymbol{A}

這樣就有，

\begin{array}[ccc]{} [a^{\prime}, b^{\prime}] \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} &= [a^{\prime}, b^{\prime}] \;\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right] \\[1em] &= [a, b]\;\boldsymbol{A} \;\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right] \\[1em] &=ax + by \end{array}

上面中間兩矩陣相乘很自然就消掉了。

?逆變與協(xié)變

上面這個(gè)過程說明啥？

我們來畫龍點(diǎn)睛一下，上進(jìn)向量的坐標(biāo)是這樣變的，

\left[\begin{array}{c} x^{\prime} \\ y^{\prime} \end{array}\right]=\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right]

有個(gè)矩陣求逆是吧，所以叫逆變。

而你躺平向量是這樣變的，

[a^{\prime}, b^{\prime}] = [a, b]\;\boldsymbol{A}

直接用了基的變換矩陣，不需要求逆矩陣。換句話說就是跟基一樣的變化，所以叫協(xié)變。

所以，大家明白了嗎？所謂上進(jìn)向量，得逆勢(shì)而上，自然是要有頑強(qiáng)的拼搏精神。而躺平向量比較佛系，順勢(shì)而躺即可。

逆勢(shì)而上，順勢(shì)而躺。

需要注意的是，躺平向量和上進(jìn)向量其實(shí)是在不同的空間里的。上進(jìn)向量所在的空間就是我們一般指的向量空間，而躺平向量是在這個(gè)向量空間的對(duì)偶空間里。你也可以把它叫做對(duì)象空間，即你對(duì)象所在的空間。

你，作為躺平向量，和某個(gè)上進(jìn)向量搞出某個(gè)小孩，是你本身固有的能力，是不會(huì)因?yàn)橄蛄靠臻g用的基不同而改變的。就是說，你和某個(gè)指定的上進(jìn)向量的坐標(biāo)在基改變后也都改了，但是你倆出來的娃（函數(shù)值）是不變的。

?小結(jié)一下

張量，從數(shù)學(xué)上看就是一個(gè)多重線性函數(shù)，應(yīng)用到幾何上就對(duì)應(yīng)一個(gè)幾何量，應(yīng)用到物體上就對(duì)應(yīng)一個(gè)物理量。這些張量吃進(jìn)若干個(gè)上進(jìn)向量和躺平向量，吐出一個(gè)實(shí)數(shù)，吃進(jìn)去的向量是會(huì)隨著向量空間的基改變而改變，或逆變或協(xié)變，而這些吐出的數(shù)并不會(huì)隨著基的改變而改變。從形式上看，這些張量在給定的基下面對(duì)應(yīng)一個(gè)具體的多維數(shù)組，這個(gè)數(shù)組也會(huì)隨著基的改變而規(guī)律地改變。

上面的例子中，你這個(gè)躺平向量與任意上進(jìn)向量搞事情的這個(gè)線性函數(shù)就是一個(gè)張量。注意，這個(gè)函數(shù)的輸入是一個(gè)上進(jìn)向量，即吃進(jìn)一個(gè)上進(jìn)向量，吐出一個(gè)實(shí)數(shù)。而這一切都是你這個(gè)躺平向量決定的。這里的張量，不是指你這個(gè)躺平向量，而是指你和上進(jìn)向量搞某個(gè)事情的本領(lǐng)。這個(gè)本領(lǐng)就是一個(gè)線性函數(shù)，即

\mathcal{F}_{你}(上進(jìn)向量 X) = 你和上進(jìn)向量搗鼓出來的一個(gè)實(shí)數(shù)

而且這個(gè)本領(lǐng)不會(huì)隨著基（坐標(biāo)系）的改變而改變。但是你和那些上進(jìn)向量是會(huì)隨著基的改變而改變的，只是改變的方式不一樣。而你和它們搞事情的本領(lǐng)（張量）是不會(huì)隨著第三者視角不同而不同的，可以認(rèn)為是一種客觀存在。

總之，給定一個(gè)躺平向量，就能像上面那樣定義一個(gè)張量。那么小明同學(xué)可能又要問了，給定一個(gè)上進(jìn)向量呢？能不能也定義一個(gè)張量呢？

還真可以，還是上面那個(gè)搞事情法子。給定一個(gè)上進(jìn)向量，它可以和很多躺平向量搞事情啊。比如，還是搞剛才那個(gè)事情，

[u, v] \begin{bmatrix} c \\ d \end{bmatrix} = uc + vd

改成函數(shù)形式，

\mathcal{F}_{\begin{bmatrix} c \\ d \end{bmatrix}}\left([u, v]\right) = uc + vd

只不過，這個(gè)時(shí)候，上進(jìn)向量是固定的，躺平向量是任意的。

其實(shí)，我們這里講的這個(gè)搞事情的法子就對(duì)應(yīng)了兩個(gè)張量，一個(gè)是型張量，一個(gè)是型張量。這個(gè)時(shí)候，你應(yīng)該拉到上面再來重新看一下型張量的定義。

?靈魂之問

最后來回答一個(gè)靈魂之問：為什么要躺平？

從上面的例子來看，躺平不就是為了和上進(jìn)青年一起搞事情嘛。對(duì)，躺下來就是為了睡上進(jìn)青年。

你上進(jìn)，我躺平，此消彼長(zhǎng)，活不變。

是不是多少有幾分，

躲進(jìn)小樓成一統(tǒng)，管他冬夏與春秋。4

小明又舉手了

這時(shí)，小明的同學(xué)又舉手了，問：老師，如果兩個(gè)上進(jìn)向量或兩個(gè)躺平向量，能一起搞事情（張量）嗎？

老師：這不就是搞基嘛，也不是不行啊，只不過跟上面的例子不同，要其他搞法啦。

怎么搞基，還有上文中的對(duì)偶空間具體怎么肥事，我們下回再聊。

什么是張量？你躺平一下就知道了。