機器學習太難？那是你沒學好線性代數(shù)

高考剛結束，之前不少人讓我推薦專業(yè)，對理工科的同學，我一般會說，如果你沒有特別執(zhí)著的專業(yè)方向，就報數(shù)學系好了。

?

其實小時候我也想不明白學好數(shù)學有什么用，直到后來學了工程數(shù)學之后，才意識到原來數(shù)學可以應用在各類工程中，尤其對技術人來說，學好線性代數(shù)就尤為重要。

?

為什么？線性代數(shù)是數(shù)值代數(shù)的數(shù)學理論前提，數(shù)值代數(shù)通常也稱為矩陣計算，是以計算機為工具來求解各種數(shù)學模型，是特別為計算機上進行線性代數(shù)計算服務的，所以，計算機科學本身就離不開線性代數(shù)的知識。

?

作為數(shù)學中最抽象的一門課，線性代數(shù)的應用十分廣泛，是計算機很多領域的基礎。比如，如何讓 3D 圖形顯示到二維屏幕上？這是線性代數(shù)在圖形圖像學中的應用。如何提高密碼被破譯的難度？這個密碼學問題，用線性代數(shù)中的有限向量空間也可以很好地解決。

?

還有一個眾所周知非常重要的應用領域 —— 機器學習。在我看來，機器學習的本質就是求解線性方程組。

?

很多人都覺得，機器學習很難，其實我感覺，機器學習本身沒有多大難度，因為經(jīng)過多年的積累后，很多規(guī)則已經(jīng)成型了。對于我們來說真正難的，是機器學習背后的算法所涉及的基礎數(shù)學原理，包括向量、矩陣等等。

?

我們可以來看下機器學習的整個知識體系。?

? ? ? ?

? ? ?

就單從數(shù)學角度來看，這個覆蓋范圍已經(jīng)很廣了，但你看，最最核心的還是線性代數(shù)，也就是最本質的向量和矩陣。所以說，學好線性代數(shù)才是最最關鍵的。

?

有些同學可能會說，線性代數(shù)對我好像沒用，是的，如果你工作中除了 CRUD 就是處理各類字符串、鏈表、Hash 表，高中甚至初中數(shù)學就足夠了。但只要你想「再往上走一步」，做任何一點帶有創(chuàng)新性的技術，數(shù)學問題，往往會成為你的絆腳石。

線代這么難，怎么才能更輕松地學懂、會用呢？

?

我以前學習的時候，啃了不少線代相關的書，但大都是直接講應用實踐，再穿插了一些數(shù)學知識，從實踐的角度切入，雖然入門容易，但缺點也顯而易見的。這樣學下來，只知道固定的應用場景，死記硬背幾個知識點容易，但是數(shù)學底層知識不牢固，當真正遇到問題的時候，也只能干瞪眼了。

?

所以在技術領域里，我更推薦從底層基礎概念開始，一步步往上走，一直到應用實踐。

但是我尋尋覓覓一直沒有找到這樣的課程，直到我看到了極客時間推出了《重學線性代數(shù)》以通俗易懂的語言，帶你構建完整實用的線代知識框架，還詳解 9 個機器學習中必備的線代核心點，并且，還會講到線性代數(shù)在計算機很多其他領域的基礎和應用，比如：圖形圖像、密碼學，等等，我確定，這就是我要找的線性代數(shù)的學習專欄，真正地能讓大家掌握工程應用中的線代知識。

?

?掃我的二維碼，免費試讀

結算用口令「xiandai66」再減￥6

到手?￥49，2?天后恢復￥68

作者是誰？

作者是朱維剛，畢埃慕（BIM）首席戰(zhàn)略官、副總裁，前阿里云資深產(chǎn)品與技術專家，微軟人工智能金牌講師，長期專注于云計算和大數(shù)據(jù)領域。擁有多年海外工作經(jīng)驗，自2008年開始從事云計算和大數(shù)據(jù)相關工作，曾帶領國際團隊主導比利時電信云 BeCloud，以及新加坡政府云 G-Cloud 的建設。

?

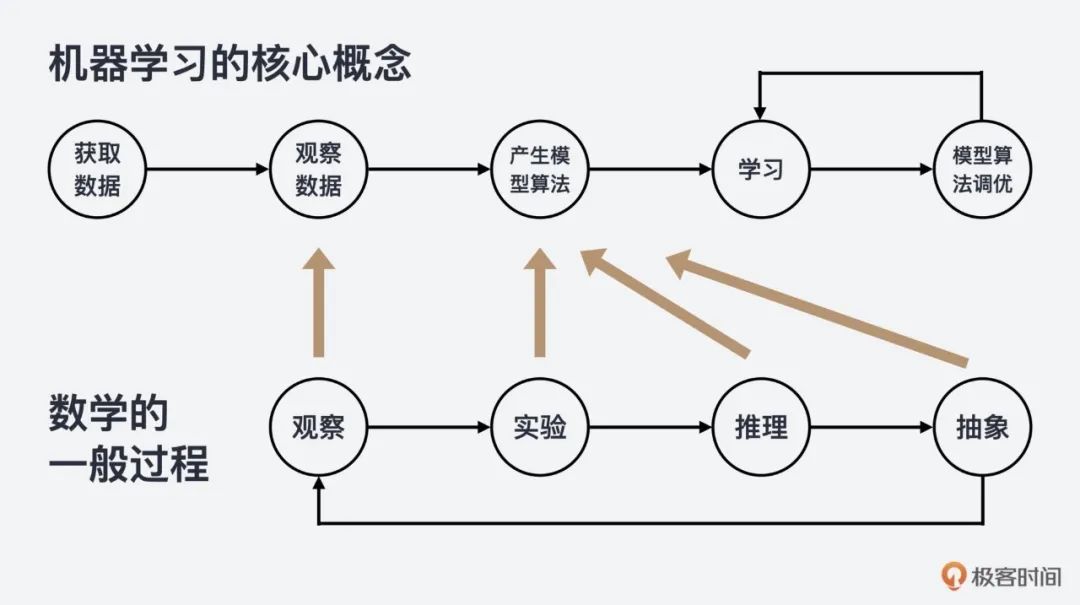
他是如何講解線性代數(shù)？

?

我看了目錄和最新更新的內(nèi)容，專欄非常系統(tǒng)，從核心概念、完整框架，再到工程應用，讓你徹底學透線代，還有不少代碼示例?

具體點說，分為 2 個模塊：

?

基礎篇，講的是線性代數(shù)的理論基礎。

?

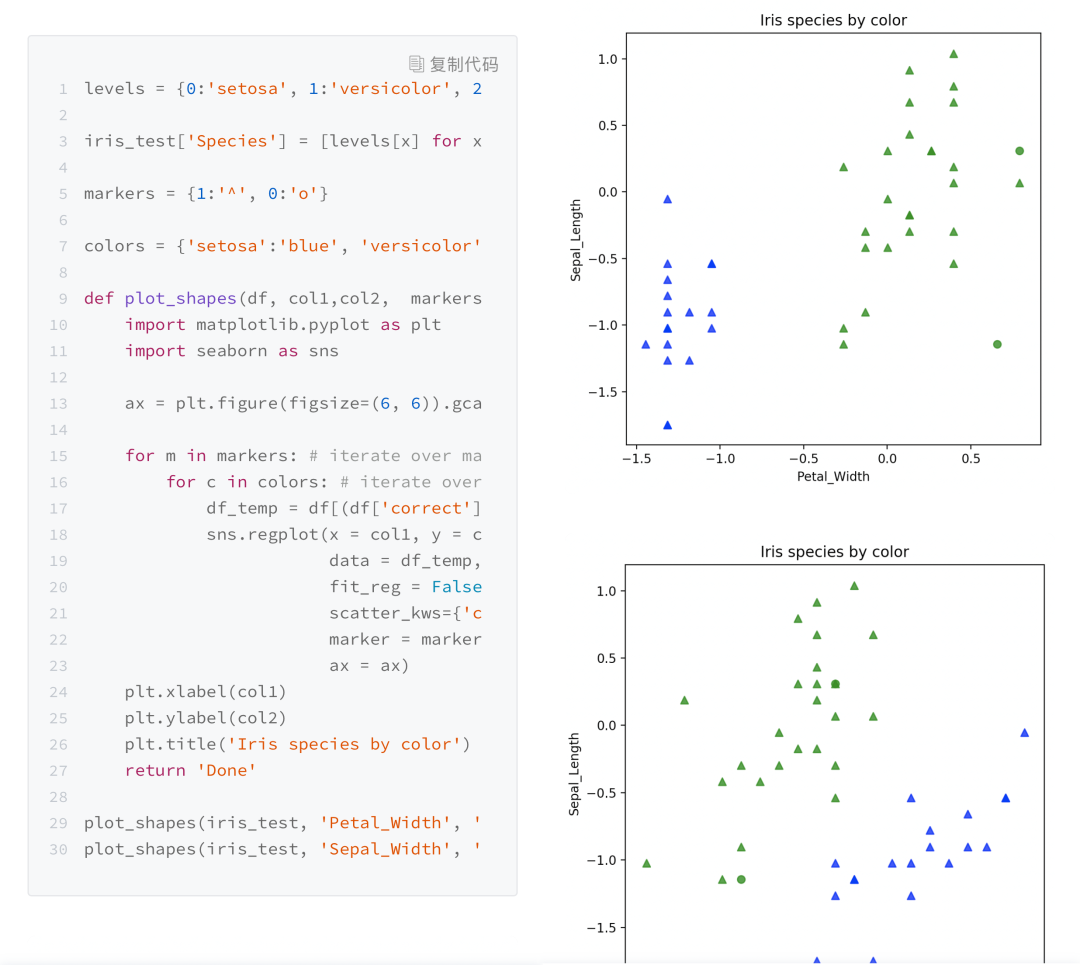
• 先從最簡單的線性方程組說起，在這基礎上引出向量和矩陣，并通過矩陣來解線性方程組的不同方法。?

• 然后，在向量和矩陣的基礎上講線性空間，因為在實踐中，更多的是對集合的操作，也就是對線性空間的操作。線性空間好比是容器，它包含了向量，以及向量的運算。?

• 最后，介紹解析幾何，是解析幾何使得向量從抽象走向了具象，讓向量具有了幾何的含義，比如：計算向量的長度、之間的距離和角度，這在機器學習的主成分分析PCA中是非常有用的。

?

第二個模塊是應用篇，結合線性代數(shù)的基礎理論，講解線性代數(shù)在計算機科學中的應用。

??

所以從整體來說，“重學線性代數(shù)”可以滿足你四個層次的需求：

?

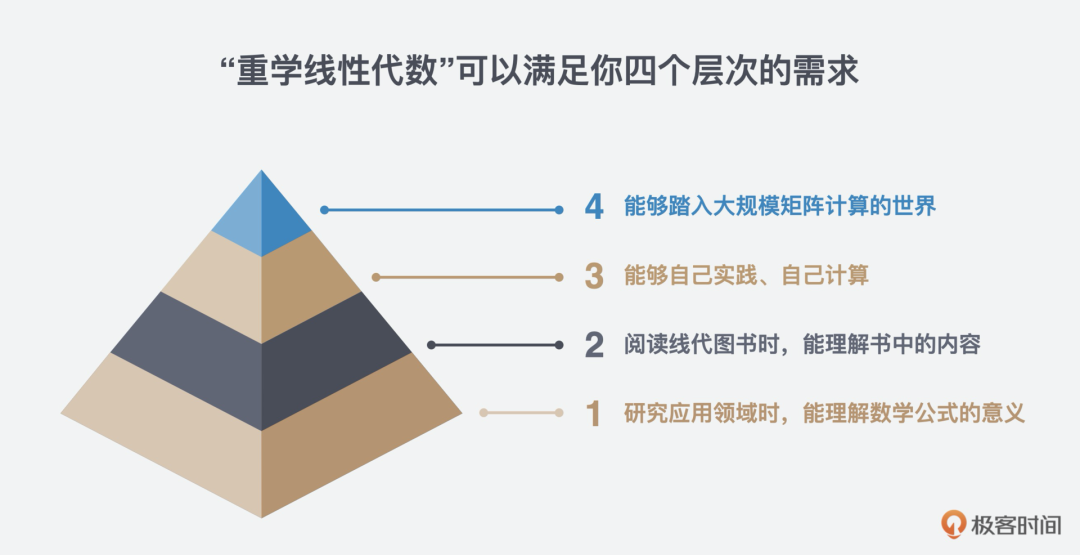
• 第一層次：在研究應用領域時，希望能夠理解數(shù)學公式的意義。
• 第二層次：在閱讀線性代數(shù)參考書時，希望理解書中的內(nèi)容。
• 第三層次：能夠自己實踐、自己計算。
• 第四層次：能夠踏入大規(guī)模矩陣計算的世界。

?? ? ? ??? ? ??

話不多說，大家自己看看目錄吧 ?

? ? ? ??

訂閱福利

?掃我的二維碼，免費試讀

結算用口令「xiandai66」再減￥6

到手?￥49，2?天后恢復￥68

點擊「閱讀原文」可直接購買，記得使用優(yōu)惠口令「xiandai66」，以最優(yōu)惠價?￥49 入手，最后 2 天了，抓緊。