大香蕉大香蕉欧美,天天天天天天干,人妻中文一区在线,韩国一区二区在线观看,国产精品久久久久久9999,无码区精品区一区二区三区,天堂资源网,淫荡人妻视频

最近有粉絲和我交流面試遇到的算法題。其中有一道題比較有意思，分享給大家。

ta 說(shuō)自己面試了一家某大型區(qū)塊鏈的公司的前端崗位，被問(wèn)到了一道算法題。這道題也是一個(gè)非常常見(jiàn)的題目了，力扣中也有原題 110. 平衡二叉樹(shù)^[1]，難度為簡(jiǎn)單。

不過(guò)面試官做了一點(diǎn)點(diǎn)小的擴(kuò)展，「難度瞬間升級(jí)了」。我們來(lái)看下面試官做了什么擴(kuò)展。

題目

題目是《判斷一棵樹(shù)是否為平衡二叉樹(shù)》，所謂平衡二叉樹(shù)指的是「二叉樹(shù)中所有節(jié)點(diǎn)的」左右子樹(shù)的深度之差不超過(guò) 1。輸入?yún)?shù)是二叉樹(shù)的根節(jié)點(diǎn) root，輸出是一個(gè) bool 值。

代碼會(huì)被以如下的方式調(diào)用：

console.log(isBalance([3, 9, 2, null, null, 5, 5]));

console.log(isBalance([1, 1, 2, 3, 4, null, null, 4, 4]));

思路

求解的思路就是圍繞著二叉樹(shù)的定義來(lái)進(jìn)行即可。

對(duì)于二叉樹(shù)中的每一個(gè)節(jié)點(diǎn)都：

分別計(jì)算左右子樹(shù)的高度，如果高度差大于 1，直接返回 false
否則繼續(xù)遞歸調(diào)用左右子節(jié)點(diǎn)，如果左右子節(jié)點(diǎn)全部都是平衡二叉樹(shù)，那么返回 true。否則返回 false

可以看出我們的算法就是「死扣定義」。

計(jì)算節(jié)點(diǎn)深度比較容易，既可以使用前序遍歷 + 參考擴(kuò)展的方式，也可使用后序遍歷的方式，這里我用的是「前序遍歷 + 參數(shù)擴(kuò)展」。

?
對(duì)此不熟悉的強(qiáng)烈建議看一下這篇文章幾乎刷完了力扣所有的樹(shù)題，我發(fā)現(xiàn)了這些東西。。。^{[2] 幾乎刷完了力扣所有的樹(shù)題，我發(fā)現(xiàn)了這些東西。。。}
?

于是你可以寫(xiě)出如下的代碼。

function getDepth(root, d = 0) {
  if (!root) return 0;
  return max(getDepth(root.left, d + 1), getDepth(root.right, d + 1));
}

function dfs(root) {
  if (!root) return true;
  if (abs(getDepth(root.left), getDepth(root.right)) > 1) return false;
  return dfs(root.left) && dfs(root.right);
}

function isBalance(root) {
  return dfs(root);
}

不難發(fā)現(xiàn)，這道題的結(jié)果和節(jié)點(diǎn)（TreeNode）的 val 沒(méi)有任何關(guān)系，val 是多少完全不影響結(jié)果。

這就完了么？

可以仔細(xì)觀察題目給的使用示例，會(huì)發(fā)現(xiàn)題目給的是 nodes 數(shù)組，并不是二叉樹(shù)的根節(jié)點(diǎn) root。

因此我們需要先「構(gòu)建二叉樹(shù)。」 構(gòu)建二叉樹(shù)本質(zhì)上是一個(gè)反序列的過(guò)程。要想知道如何反序列化，肯定要先知道序列化。

「而二叉樹(shù)序列的方法有很多啊？題目給的是哪種呢？這需要你和面試官溝通。很有可能面試官在等著你問(wèn)他呢！！！」

反序列化

我們先來(lái)看下什么是序列化，以下定義來(lái)自維基百科：

?
序列化（serialization）在計(jì)算機(jī)科學(xué)的數(shù)據(jù)處理中，是指將數(shù)據(jù)結(jié)構(gòu)或?qū)ο鬆顟B(tài)轉(zhuǎn)換成可取用格式（例如存成文件，存于緩沖，或經(jīng)由網(wǎng)絡(luò)中發(fā)送），以留待后續(xù)在相同或另一臺(tái)計(jì)算機(jī)環(huán)境中，能恢復(fù)原先狀態(tài)的過(guò)程。依照序列化格式重新獲取字節(jié)的結(jié)果時(shí)，可以利用它來(lái)產(chǎn)生與原始對(duì)象相同語(yǔ)義的副本。對(duì)于許多對(duì)象，像是使用大量引用的復(fù)雜對(duì)象，這種序列化重建的過(guò)程并不容易。面向?qū)ο笾械膶?duì)象序列化，并不概括之前原始對(duì)象所關(guān)系的函數(shù)。這種過(guò)程也稱為對(duì)象編組（marshalling）。從一系列字節(jié)提取數(shù)據(jù)結(jié)構(gòu)的反向操作，是反序列化（也稱為解編組、deserialization、unmarshalling）。
?

可見(jiàn)，序列化和反序列化在計(jì)算機(jī)科學(xué)中的應(yīng)用還是非常廣泛的。就拿 LeetCode 平臺(tái)來(lái)說(shuō)，其允許用戶輸入形如：

[1,2,3,null,null,4,5]

這樣的數(shù)據(jù)結(jié)構(gòu)來(lái)描述一顆樹(shù)：

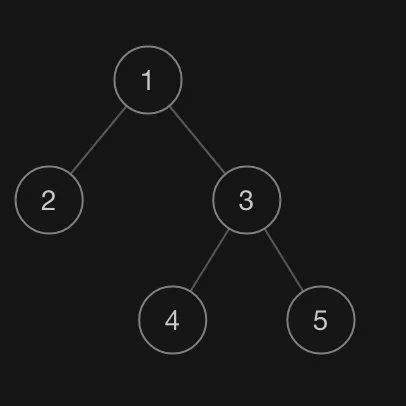
([1,2,3,null,null,4,5] 對(duì)應(yīng)的二叉樹(shù))

其實(shí)序列化和反序列化只是一個(gè)概念，不是一種具體的算法，而是很多的算法。并且針對(duì)不同的數(shù)據(jù)結(jié)構(gòu)，算法也會(huì)不一樣。

前置知識(shí)

閱讀本文之前，需要你對(duì)樹(shù)的遍歷以及 BFS 和 DFS 比較熟悉。如果你還不熟悉，推薦閱讀一下相關(guān)文章之后再來(lái)看。或者我這邊也寫(xiě)了一個(gè)總結(jié)性的文章二叉樹(shù)的遍歷^[3]，你也可以看看。

前言

我們知道：二叉樹(shù)的深度優(yōu)先遍歷，根據(jù)訪問(wèn)根節(jié)點(diǎn)的順序不同，可以將其分為前序遍歷，中序遍歷, 后序遍歷。即如果先訪問(wèn)根節(jié)點(diǎn)就是前序遍歷，最后訪問(wèn)根節(jié)點(diǎn)就是后序遍歷，其它則是中序遍歷。而左右節(jié)點(diǎn)的相對(duì)順序是不會(huì)變的，一定是先左后右。

?
當(dāng)然也可以設(shè)定為先右后左。
?

并且知道了三種遍歷結(jié)果中的任意兩種即可還原出原有的樹(shù)結(jié)構(gòu)。這不就是序列化和反序列化么？如果對(duì)這個(gè)比較陌生的同學(xué)建議看看我之前寫(xiě)的《構(gòu)造二叉樹(shù)系列》^[4]

有了這樣一個(gè)前提之后算法就自然而然了。即先對(duì)二叉樹(shù)進(jìn)行兩次不同的遍歷，不妨假設(shè)按照前序和中序進(jìn)行兩次遍歷。然后將兩次遍歷結(jié)果序列化，比如將兩次遍歷結(jié)果以逗號(hào)“,” join 成一個(gè)字符串。之后將字符串反序列即可，比如將其以逗號(hào)“,” split 成一個(gè)數(shù)組。

序列化：

class Solution:
    def preorder(self, root: TreeNode):
        if not root: return []
        return [str(root.val)] +self. preorder(root.left) + self.preorder(root.right)
    def inorder(self, root: TreeNode):
        if not root: return []
        return  self.inorder(root.left) + [str(root.val)] + self.inorder(root.right)
    def serialize(self, root):
        ans = ''
        ans += ','.join(self.preorder(root))
        ans += '$'
        ans += ','.join(self.inorder(root))

        return ans

反序列化：

這里我直接用了力扣 105. 從前序與中序遍歷序列構(gòu)造二叉樹(shù) 的解法，一行代碼都不改。

class Solution:
    def deserialize(self, data: str):
        preorder, inorder = data.split('$')
        if not preorder: return None
        return self.buildTree(preorder.split(','), inorder.split(','))

    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        # 實(shí)際上inorder 和 preorder 一定是同時(shí)為空的，因此你無(wú)論判斷哪個(gè)都行
        if not preorder:
            return None
        root = TreeNode(preorder[0])

        i = inorder.index(root.val)
        root.left = self.buildTree(preorder[1:i + 1], inorder[:i])
        root.right = self.buildTree(preorder[i + 1:], inorder[i+1:])

        return root

實(shí)際上這個(gè)算法是不一定成立的，原因在于樹(shù)的節(jié)點(diǎn)可能存在重復(fù)元素。也就是說(shuō)我前面說(shuō)的知道了三種遍歷結(jié)果中的任意兩種即可還原出原有的樹(shù)結(jié)構(gòu)是不對(duì)的，嚴(yán)格來(lái)說(shuō)應(yīng)該是「如果樹(shù)中不存在重復(fù)的元素，那么知道了三種遍歷結(jié)果中的任意兩種即可還原出原有的樹(shù)結(jié)構(gòu)」。

聰明的你應(yīng)該發(fā)現(xiàn)了，上面我的代碼用了 i = inorder.index(root.val)，如果存在重復(fù)元素，那么得到的索引 i 就可能不是準(zhǔn)確的。但是，如果題目限定了沒(méi)有重復(fù)元素則可以用這種算法。但是現(xiàn)實(shí)中不出現(xiàn)重復(fù)元素不太現(xiàn)實(shí)，因此需要考慮其他方法。那究竟是什么樣的方法呢?

答案是「記錄空節(jié)點(diǎn)」。接下來(lái)進(jìn)入正題。

DFS

序列化

我們來(lái)模仿一下力扣的記法。比如：[1,2,3,null,null,4,5](本質(zhì)上是 BFS 層次遍歷)，對(duì)應(yīng)的樹(shù)如下：

?
選擇這種記法，而不是 DFS 的記法的原因是看起來(lái)比較直觀。并不代表我們這里是要講 BFS 的序列化和反序列化。
?

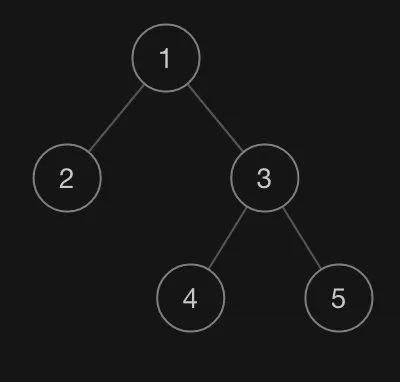
序列化的代碼非常簡(jiǎn)單，我們只需要在普通的遍歷基礎(chǔ)上，增加對(duì)空節(jié)點(diǎn)的輸出即可（普通的遍歷是不處理空節(jié)點(diǎn)的）。

比如我們都樹(shù)進(jìn)行一次前序遍歷的同時(shí)增加空節(jié)點(diǎn)的處理。選擇前序遍歷的原因是容易知道根節(jié)點(diǎn)的位置，并且代碼好寫(xiě)，不信你可以試試。

因此序列化就僅僅是普通的 DFS 而已，直接給大家看看代碼。

Python 代碼：

class Codec:
    def serialize_dfs(self, root, ans):
        # 空節(jié)點(diǎn)也需要序列化，否則無(wú)法唯一確定一棵樹(shù)，后不贅述。
        if not root: return ans + '#,'
        # 節(jié)點(diǎn)之間通過(guò)逗號(hào)（,）分割
        ans += str(root.val) + ','
        ans = self.serialize_dfs(root.left, ans)
        ans = self.serialize_dfs(root.right, ans)
        return ans
    def serialize(self, root):
        # 由于最后會(huì)添加一個(gè)額外的逗號(hào)，因此需要去除最后一個(gè)字符，后不贅述。
        return self.serialize_dfs(root, '')[:-1]

Java 代碼：

public class Codec {
    public String serialize_dfs(TreeNode root, String str) {
        if (root == null) {
            str += "None,";
        } else {
            str += str.valueOf(root.val) + ",";
            str = serialize_dfs(root.left, str);
            str = serialize_dfs(root.right, str);
        }
        return str;
    }

    public String serialize(TreeNode root) {
        return serialize_dfs(root, "");
    }
}

[1,2,3,null,null,4,5] 會(huì)被處理為1,2,#,#,3,4,#,#,5,#,#

反序列化

反序列化的第一步就是將其展開(kāi)。以上面的例子來(lái)說(shuō)，則會(huì)變成數(shù)組：[1,2,#,#,3,4,#,#,5,#,#]，然后我們同樣執(zhí)行一次前序遍歷，每次處理一個(gè)元素，重建即可。由于我們采用的前序遍歷，因此第一個(gè)是根元素，下一個(gè)是其左子節(jié)點(diǎn)，下下一個(gè)是其右子節(jié)點(diǎn)。

Python 代碼：

    def deserialize_dfs(self, nodes):
        if nodes:
            if nodes[0] == '#':
                nodes.pop(0)
                return None
            root = TreeNode(nodes.pop(0))
            root.left = self.deserialize_dfs(nodes)
            root.right = self.deserialize_dfs(nodes)
            return root
        return None

    def deserialize(self, data: str):
        nodes = data.split(',')
        return self.deserialize_dfs(nodes)

Java 代碼：

    public TreeNode deserialize_dfs(List<String> l) {
        if (l.get(0).equals("None")) {
            l.remove(0);
            return null;
        }

        TreeNode root = new TreeNode(Integer.valueOf(l.get(0)));
        l.remove(0);
        root.left = deserialize_dfs(l);
        root.right = deserialize_dfs(l);

        return root;
    }

    public TreeNode deserialize(String data) {
        String[] data_array = data.split(",");
        List<String> data_list = new LinkedList<String>(Arrays.asList(data_array));
        return deserialize_dfs(data_list);
    }

「復(fù)雜度分析」

時(shí)間復(fù)雜度：每個(gè)節(jié)點(diǎn)都會(huì)被處理一次，因此時(shí)間復(fù)雜度為，其中為節(jié)點(diǎn)的總數(shù)。
空間復(fù)雜度：空間復(fù)雜度取決于棧深度，因此空間復(fù)雜度為，其中為樹(shù)的深度。

BFS

序列化

實(shí)際上我們也可以使用 BFS 的方式來(lái)表示一棵樹(shù)。在這一點(diǎn)上其實(shí)就和力扣的記法是一致的了。

我們知道層次遍歷的時(shí)候?qū)嶋H上是有層次的。只不過(guò)有的題目需要你記錄每一個(gè)節(jié)點(diǎn)的層次信息，有些則不需要。

這其實(shí)就是一個(gè)樸實(shí)無(wú)華的 BFS，唯一不同則是增加了空節(jié)點(diǎn)。

Python 代碼：


class Codec:
    def serialize(self, root):
        ans = ''
        queue = [root]
        while queue:
            node = queue.pop(0)
            if node:
                ans += str(node.val) + ','
                queue.append(node.left)
                queue.append(node.right)
            else:
                ans += '#,'
        return ans[:-1]

反序列化

如圖有這樣一棵樹(shù)：

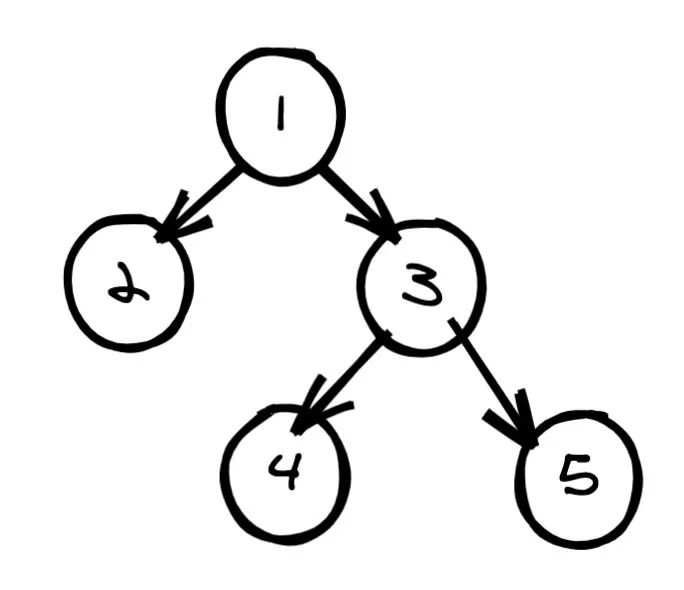
那么其層次遍歷為 [1,2,3,#,#, 4, 5]。我們根據(jù)此層次遍歷的結(jié)果來(lái)看下如何還原二叉樹(shù)，如下是我畫(huà)的一個(gè)示意圖：

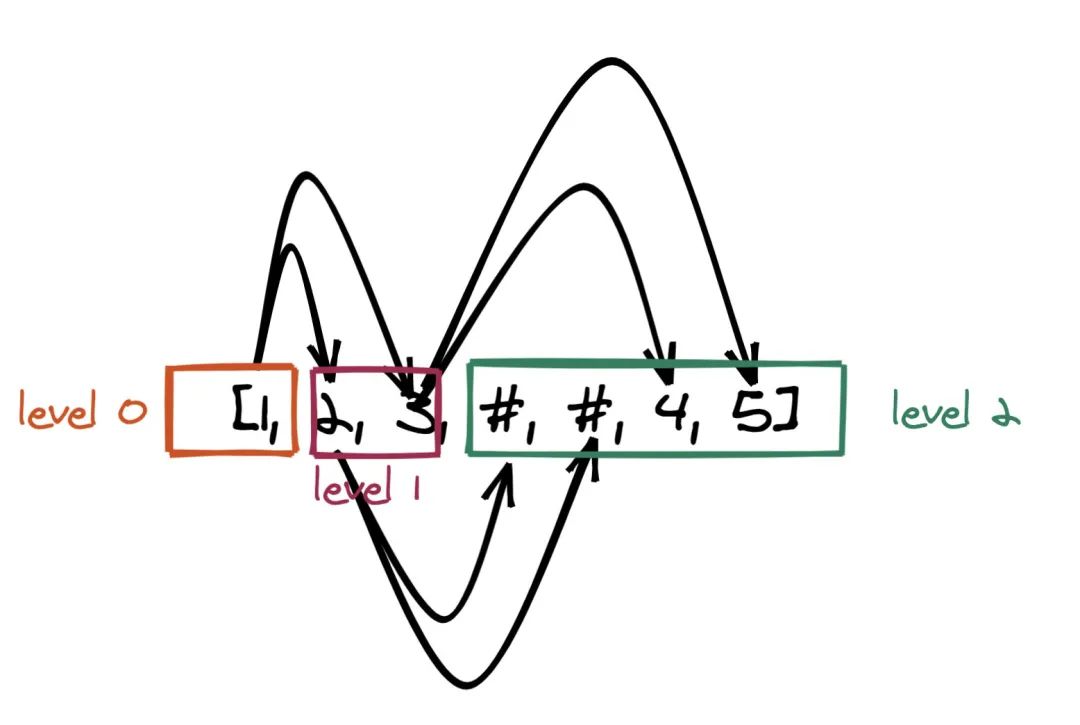
動(dòng)畫(huà)演示：

容易看出：

level x 的節(jié)點(diǎn)一定指向 level x + 1 的節(jié)點(diǎn)，如何找到 level + 1 呢？這很容易通過(guò)層次遍歷來(lái)做到。
對(duì)于給的的 level x，從左到右依次對(duì)應(yīng) level x + 1 的節(jié)點(diǎn)，即第 1 個(gè)節(jié)點(diǎn)的左右子節(jié)點(diǎn)對(duì)應(yīng)下一層的第 1 個(gè)和第 2 個(gè)節(jié)點(diǎn)，第 2 個(gè)節(jié)點(diǎn)的左右子節(jié)點(diǎn)對(duì)應(yīng)下一層的第 3 個(gè)和第 4 個(gè)節(jié)點(diǎn)。。。
接上，其實(shí)如果你仔細(xì)觀察的話，實(shí)際上 level x 和 level x + 1 的判斷是無(wú)需特別判斷的。我們可以把思路逆轉(zhuǎn)過(guò)來(lái)：即第 1 個(gè)節(jié)點(diǎn)的左右子節(jié)點(diǎn)對(duì)應(yīng)第 1 個(gè)和第 2 個(gè)節(jié)點(diǎn)，第 2 個(gè)節(jié)點(diǎn)的左右子節(jié)點(diǎn)對(duì)應(yīng)第 3 個(gè)和第 4 個(gè)節(jié)點(diǎn)。。。（注意，沒(méi)了下一層三個(gè)字）

因此我們的思路也是同樣的 BFS，并依次連接左右節(jié)點(diǎn)。

Python 代碼：

    def deserialize(self, data: str):
        if data == '#': return None
        # 數(shù)據(jù)準(zhǔn)備
        nodes = data.split(',')
        if not nodes: return None
        # BFS
        root = TreeNode(nodes[0])
        queue = collections.deque([root])
        # 已經(jīng)有 root 了，因此從 1 開(kāi)始
        i = 1

        while i < len(nodes) - 1:
            node = queue.popleft()
            lv = nodes[i]
            rv = nodes[i + 1]
            i += 2
            # 對(duì)于給的的 level x，從左到右依次對(duì)應(yīng) level x + 1 的節(jié)點(diǎn)
            # node 是 level x 的節(jié)點(diǎn)，l 和 r 則是 level x + 1 的節(jié)點(diǎn)
            if lv != '#':
                l = TreeNode(lv)
                node.left = l
                queue.append(l)

            if rv != '#':
                r = TreeNode(rv)
                node.right = r
                queue.append(r)
        return root

復(fù)雜度分析

時(shí)間復(fù)雜度：每個(gè)節(jié)點(diǎn)都會(huì)被處理一次，因此時(shí)間復(fù)雜度為，其中為節(jié)點(diǎn)的總數(shù)。
空間復(fù)雜度：，其中為節(jié)點(diǎn)的總數(shù)。

這樣就結(jié)束了嗎？

有了上面的序列化的知識(shí)。

我們就可以問(wèn)面試官是哪種序列化的手段。并針對(duì)性選擇反序列化方案構(gòu)造出二叉樹(shù)。最后再使用本文開(kāi)頭的方法解決即可。

以為這里就結(jié)束了嗎？

并沒(méi)有！「面試官讓他說(shuō)出自己的復(fù)雜度。」

讀到這里，不妨自己暫停一下，思考這個(gè)解法的復(fù)雜度是多少？

ok，我們來(lái)揭秘。

時(shí)間復(fù)雜度是，其中是生成樹(shù)的時(shí)間，是判斷是否是平衡二叉樹(shù)的時(shí)間。

為什么判斷平衡二叉樹(shù)的時(shí)間復(fù)雜度是？這是因?yàn)槲覀儗?duì)每一個(gè)節(jié)點(diǎn)都計(jì)算其深度，因此總的時(shí)間為「所有節(jié)點(diǎn)深度之和」，最差情況是退化到鏈表的情況，此時(shí)的高度之和為，根據(jù)等差數(shù)列求和公式可知，時(shí)間復(fù)雜度是。

空間復(fù)雜度很明顯是。這其中包括了構(gòu)建二叉樹(shù)的 n 以及遞歸棧的開(kāi)銷。

面試官又追問(wèn)：可以優(yōu)化么?

讀到這里，不妨自己暫停一下，思考這個(gè)解法的復(fù)雜度是多少？

ok，我們來(lái)揭秘。

優(yōu)化的手段有兩種。第一種是：

空間換時(shí)間。將 getDepth 函數(shù)的返回值記錄下來(lái)，確保多次執(zhí)行 getDepth 且參數(shù)相同的情況不會(huì)重復(fù)執(zhí)行。這樣時(shí)間復(fù)雜度可以降低到
第二種方法和上面的方法是類似的，其本質(zhì)是記憶化遞歸(和動(dòng)態(tài)規(guī)劃類似)。

?
我在上一篇文章讀者：西法，記憶化遞歸究竟怎么改成動(dòng)態(tài)規(guī)劃啊？詳細(xì)講述了記憶化遞歸和動(dòng)態(tài)規(guī)劃的互相轉(zhuǎn)換。如果你看了的話，會(huì)發(fā)現(xiàn)這里就是記憶化遞歸。
?

第一種方法代碼比較簡(jiǎn)單，就不寫(xiě)了。這里給一下第二種方法的代碼。

定義函數(shù) getDepth(root) 返回 root 的深度。需要注意的是，「如果子節(jié)點(diǎn)不平衡，直接返回 -1。」 這樣上面的兩個(gè)函數(shù)功能（getDepth 和 isBalance）就可以放到一個(gè)函數(shù)中執(zhí)行了。

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        def getDepth(root: TreeNode) -> int:
            if not root:
                return 0
            lh = getDepth(root.left)
            rh = getDepth(root.right)
            # lh == -1 表示左子樹(shù)不平衡
            # rh == -1 表示右子樹(shù)不平衡
            if lh == -1 or rh == -1 or abs(rh - lh) > 1:
                return -1
            return max(lh, rh) + 1

        return getDepth(root) != -1

總結(jié)

雖然這道面試題目是一個(gè)常見(jiàn)的常規(guī)題。不過(guò)參數(shù)改了一下，瞬間難度就上來(lái)了。如果面試官?zèng)]有直接給你說(shuō) nodes 是怎么序列化來(lái)的，他可能是故意的。「二叉樹(shù)序列的方法有很多啊？題目給的是哪種呢？這需要你和面試官溝通。很有可能面試官在等著你問(wèn)他呢！！！」 這正是這道題的難點(diǎn)所在。

構(gòu)造二叉樹(shù)本質(zhì)就是一個(gè)二叉樹(shù)反序列的過(guò)程。而如何反序列化需要結(jié)合序列化算法。

序列化方法根據(jù)是否存儲(chǔ)空節(jié)點(diǎn)可以分為：存儲(chǔ)空節(jié)點(diǎn)和不存儲(chǔ)空節(jié)點(diǎn)。

存儲(chǔ)空節(jié)點(diǎn)會(huì)造成空間的浪費(fèi)，不存儲(chǔ)空節(jié)點(diǎn)會(huì)造成無(wú)法唯一確定一個(gè)包含重復(fù)值的樹(shù)。

而關(guān)于序列化，本文主要講述的是二叉樹(shù)的序列化和反序列化。看完本文之后，你就可以放心大膽地去 AC 以下兩道題：

449. 序列化和反序列化二叉搜索樹(shù)(中等)^[5]
297. 二叉樹(shù)的序列化與反序列化(困難)^[6]

另外僅僅是暴力做出來(lái)還不夠，大家要對(duì)自己提出更高的要求。

最起碼你要會(huì)分析自己的算法，常用的就是復(fù)雜度分析。進(jìn)一步如果你可以對(duì)算法進(jìn)行優(yōu)化會(huì)很加分。比如這里我就通過(guò)兩種優(yōu)化方法將時(shí)間優(yōu)化到了。

PS：我不告訴你的話，你能知道我給的第二種優(yōu)化方式就是動(dòng)態(tài)規(guī)劃么？

留言在這里

愛(ài)心三連擊

1.看到這里了就點(diǎn)個(gè)在看支持下吧，你的在看是我創(chuàng)作的動(dòng)力。

2.關(guān)注公眾號(hào)力扣加加，獲取更多前端硬核文章！加個(gè)星標(biāo)，不錯(cuò)過(guò)每一條成長(zhǎng)的機(jī)會(huì)。

3.如果你覺(jué)得本文的內(nèi)容對(duì)你有幫助，就幫我轉(zhuǎn)發(fā)一下吧。

如果喜歡我的文章，點(diǎn)個(gè)”在看“吧

Reference

[1]

110. 平衡二叉樹(shù): https://leetcode-cn.com/problems/balanced-binary-tree/

[2]

幾乎刷完了力扣所有的樹(shù)題，我發(fā)現(xiàn)了這些東西。。。: https://mp.weixin.qq.com/s?__biz=MzI4MzUxNjI3OA==&mid=2247485899&idx=1&sn=27d1c7b8ff88cbe235b7fca63227d356&chksm=eb88c5d2dcff4cc4102a036bc558b9c598fbf1c69f6ee9dc2822b0784975f8b2df8b8a7609dd&token=1914944481&lang=zh_CN#rd

[3]

二叉樹(shù)的遍歷: https://github.com/azl397985856/leetcode/blob/master/thinkings/binary-tree-traversal.md

[4]

《構(gòu)造二叉樹(shù)系列》: https://lucifer.ren/blog/2020/02/08/%E6%9E%84%E9%80%A0%E4%BA%8C%E5%8F%89%E6%A0%91%E4%B8%93%E9%A2%98/

[5]

449. 序列化和反序列化二叉搜索樹(shù)(中等): https://leetcode-cn.com/problems/serialize-and-deserialize-bst/

[6]

449. 序列化和反序列化二叉搜索樹(shù)(中等): https://leetcode-cn.com/problems/serialize-and-deserialize-binary-tree/

如果發(fā)現(xiàn)文章內(nèi)容有問(wèn)題，可以閱讀原文查看。

某區(qū)塊鏈公司竟然用這道算法題來(lái)面試

題目

思路

這就完了么？

反序列化

前置知識(shí)

前言

DFS

序列化

反序列化

BFS

序列化

反序列化

這樣就結(jié)束了嗎？

總結(jié)

愛(ài)心三連擊

Reference