【算法】894- 圖文并茂講解堆排序

作者:竹雨
https://juejin.cn/post/6932718585173753869
前言
文中用 JavaScript 實(shí)現(xiàn)算法,詳細(xì)解釋堆排序 js 中堆的創(chuàng)建與維護(hù),以及堆排序算法的實(shí)現(xiàn)堆創(chuàng)建。
理論
堆,是具有下列性質(zhì)的完全二叉樹:每個(gè)節(jié)點(diǎn)的值都小于等于其左右孩子節(jié)點(diǎn)值是小根堆;(大于等于則是大根堆)。批注:有些參考書將堆直接定義為序列,但是,從邏輯結(jié)構(gòu)上講,還是將堆定義為完全二叉樹更好。雖然堆的典型實(shí)現(xiàn)方法是數(shù)組,但從邏輯的角度上講,堆實(shí)際上是一種樹結(jié)構(gòu)。
對(duì)于數(shù)組實(shí)現(xiàn)的堆,是一個(gè)完全二叉樹,其中任意一個(gè)節(jié)點(diǎn) i 都滿足以下公式
Parent(i) = floor((i-1)/2),i 的父節(jié)點(diǎn)下標(biāo) Left(i) = 2i + 1,i 的左子節(jié)點(diǎn)下標(biāo) Right(i) = 2(i + 1),i 的右子節(jié)點(diǎn)下標(biāo)
思路
此思路用于將任意數(shù)組調(diào)整成大根堆 首先將數(shù)組想象成是一個(gè)完美二叉樹 我們的目的是將這個(gè)二叉數(shù)調(diào)整成大根堆,即每個(gè)節(jié)點(diǎn)的值都大于等于其左右孩子節(jié)點(diǎn)值 首先,尋找到最后一個(gè)根節(jié)點(diǎn),此根節(jié)點(diǎn)有一個(gè)孩子是數(shù)組的最后一個(gè)元素 然后找出大的孩子節(jié)點(diǎn)與根節(jié)點(diǎn)對(duì)比,如果大的孩子節(jié)點(diǎn)比根節(jié)點(diǎn)大,則將根節(jié)點(diǎn)與大的孩子節(jié)點(diǎn)互換,保證根節(jié)點(diǎn)最大 接著向前遍歷根節(jié)點(diǎn) 對(duì)每個(gè)根節(jié)點(diǎn),都首先找出比較大的孩子節(jié)點(diǎn),然后將大的孩子節(jié)點(diǎn)與根節(jié)點(diǎn)對(duì)比 如果孩子節(jié)點(diǎn)比根節(jié)點(diǎn)大,那么將孩子節(jié)點(diǎn)與根節(jié)點(diǎn)互換 然后將互換后得到新值的孩子節(jié)點(diǎn)作為新的根節(jié)點(diǎn),將其與它自己的子節(jié)點(diǎn)再重復(fù)以上對(duì)比,以此進(jìn)行深度遍歷的重復(fù)操作,直到此相關(guān)樹上的根節(jié)點(diǎn)都比孩子節(jié)點(diǎn)大為止 深度遍歷操作完后,繼續(xù)執(zhí)行前面的根節(jié)點(diǎn)遍歷操作,直到遍歷到最后一個(gè)根節(jié)點(diǎn)
例子
現(xiàn)有數(shù)組 arr = [5,8,3,5,2,99,22,44],將其調(diào)整為大根堆 數(shù)組可以表示堆即完美二叉樹,因此將其轉(zhuǎn)化成完美二叉樹理解(此處可自行搜索,完美二叉樹用數(shù)組表示),如下圖所示
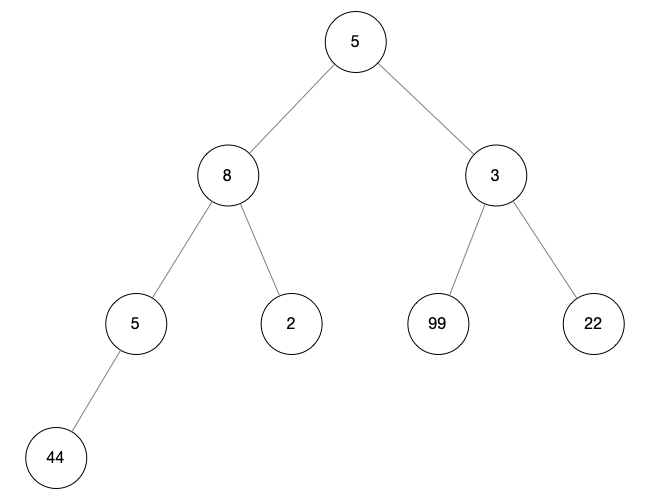
尋找最后一個(gè)根節(jié)點(diǎn),用 i 表示,從 arr.length / 2 作為初始值向前查找 當(dāng) i = arr.length / 2 = 4 時(shí)沒有孩子節(jié)點(diǎn),所以它不是根節(jié)點(diǎn) 向前遍歷節(jié)點(diǎn),當(dāng) i = 3 時(shí),它擁有孩子節(jié)點(diǎn) arr[arr.length - 1],所以 arr[3] = 5 就是我們想找的最后一個(gè)根節(jié)點(diǎn) 此時(shí)我們可以得最后一顆子樹,如下圖標(biāo)記所示
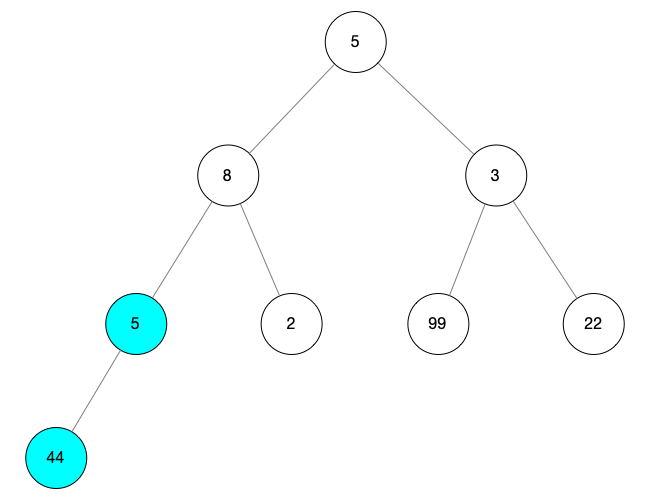
然后我們針對(duì)這顆子樹進(jìn)行調(diào)整操作
找到最大的孩子節(jié)點(diǎn),用 child 表示,此時(shí)只有一個(gè)孩子節(jié)點(diǎn) arr.length - 1,所以 child = arr.length - 1 = 7 將 child 與根節(jié)點(diǎn)(i = 3)對(duì)比,如果 child 的值 i 的值大,則互換值 此處 child 比 i 的值大所以互換值,child 的值改為 5,i 的值改為 44 由于 child 沒有孩子節(jié)點(diǎn)所以不進(jìn)行更深層次的遍歷 操作完之后如下圖所示
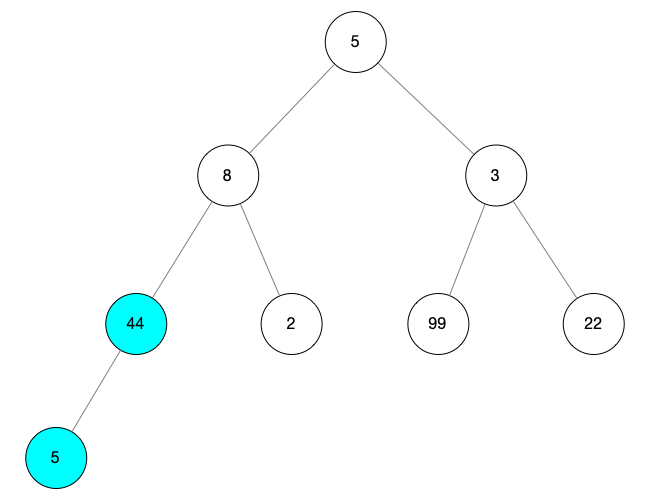
然后向前繼續(xù)尋找根節(jié)點(diǎn),當(dāng) i = 2 的時(shí)候,我們將找到一顆新的子樹
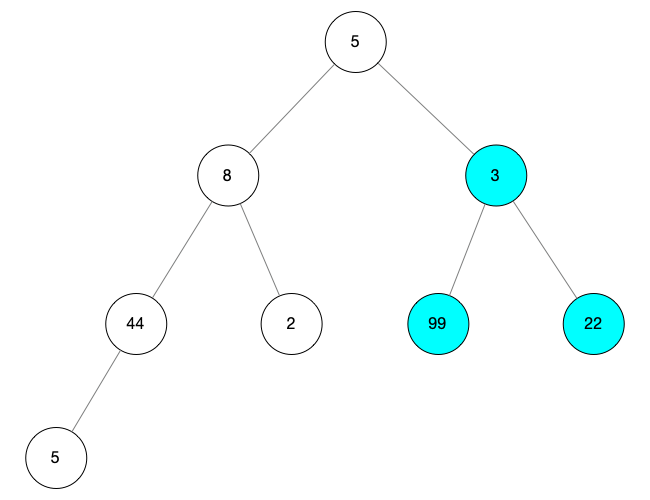
對(duì)這顆找到的樹進(jìn)行調(diào)整操作
尋找大的孩子節(jié)點(diǎn),用 child 表示,由圖可知最大的孩子節(jié)點(diǎn)的值為 99,所以 child = 5 當(dāng)前的根節(jié)點(diǎn) i = 2,由于 child 的值比 i 的值大,所以互換 同時(shí)由于 child 后面沒有孩子節(jié)點(diǎn),所以結(jié)束操作 上面操作后可得到下圖所示的樹
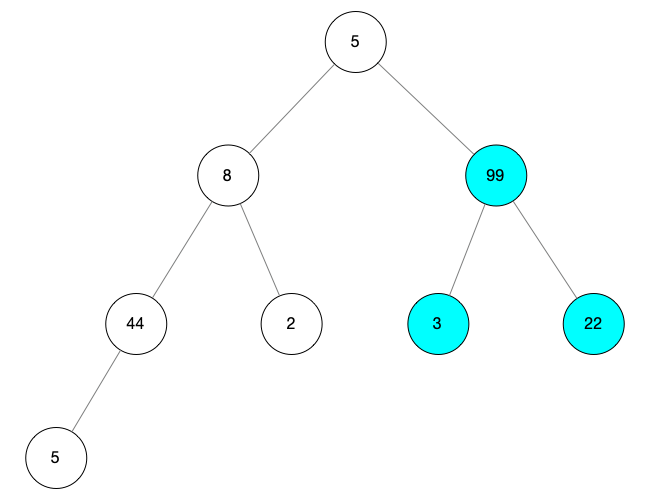
繼續(xù)向前尋找根節(jié)點(diǎn),當(dāng) i = 1 的時(shí)候,我們找到一顆新的樹
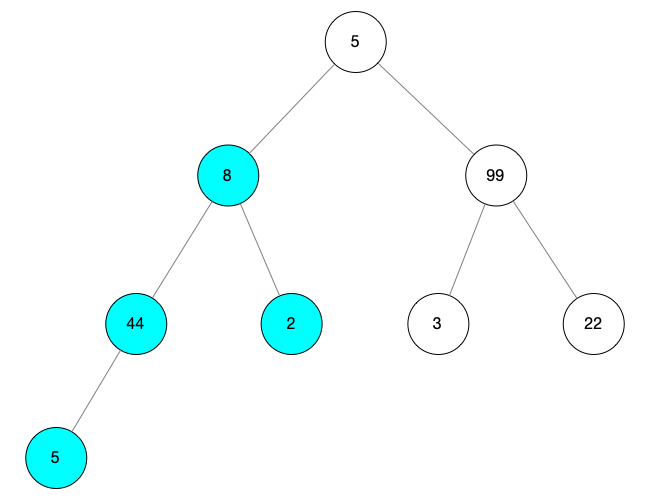
對(duì)這顆樹進(jìn)行調(diào)整操作,此時(shí) i = 1,child = 3
按照上面步驟,首先互換 child 和 i 的值
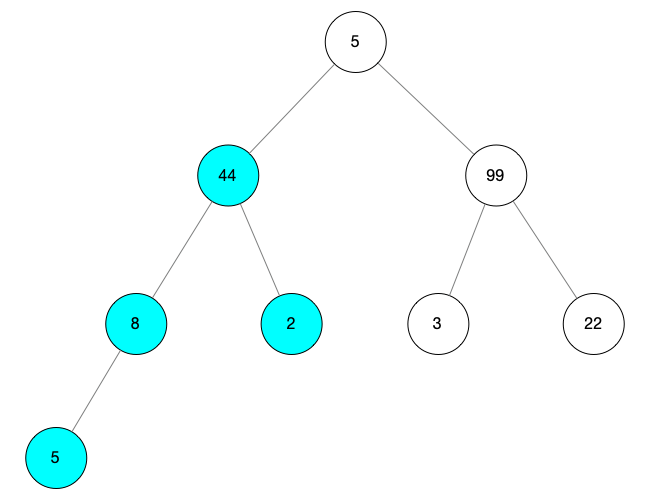
然后由于 child 有孩子節(jié)點(diǎn),所以將 i 指向 i,將 child 指向它自己的孩子節(jié)點(diǎn) 得到 i = 3, child = 7 重復(fù)比較操作,如果孩子節(jié)點(diǎn)比根節(jié)點(diǎn)大互換值 此處 arr[i] = 8,arr[child] = 5 根節(jié)點(diǎn)比孩子節(jié)點(diǎn)大,所以不替換 最終得到的樹如下圖所示

繼續(xù)向前遍歷,得到最后一顆新樹,根節(jié)點(diǎn)為 i = 0
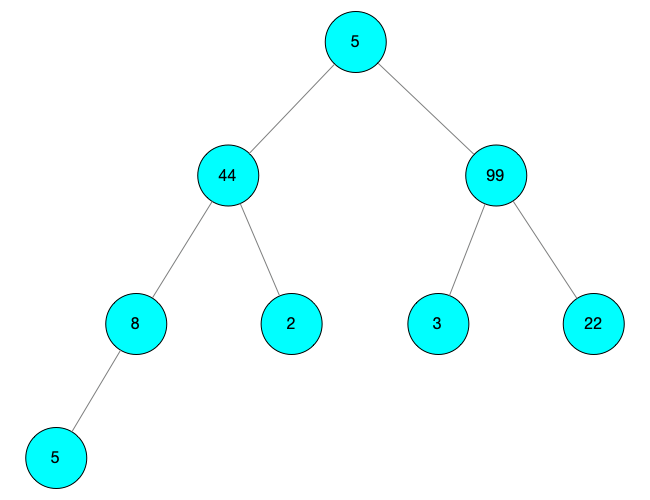
對(duì)這顆樹進(jìn)行調(diào)整操作
此時(shí) i = 0 先尋找 child = 2,arr[child] = 99 arr[child] = 99 > arr[i] = 5,互換得到 arr[child] = 5,arr[i] = 99
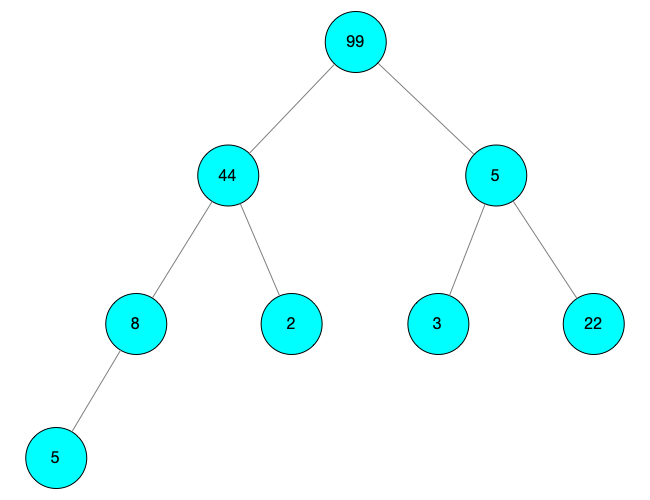
由于 child 有孩子節(jié)點(diǎn),所以對(duì) child 的孩子節(jié)點(diǎn)進(jìn)行深度調(diào)整 i = child = 2,child = 2 * i + 1 = 5 由于此時(shí)有左右兩個(gè)孩子節(jié)點(diǎn),索引分別為 5 和 6,并且索引為 6 的節(jié)點(diǎn)值比較大,所以 child 更改為 6 比較 i 與 child 的值 arr[i] = arr[2] = 5 小于 arr[child] = arr[6] = 22 所以進(jìn)行值互換,得到 arr[i] = 22,arr[child] = 5
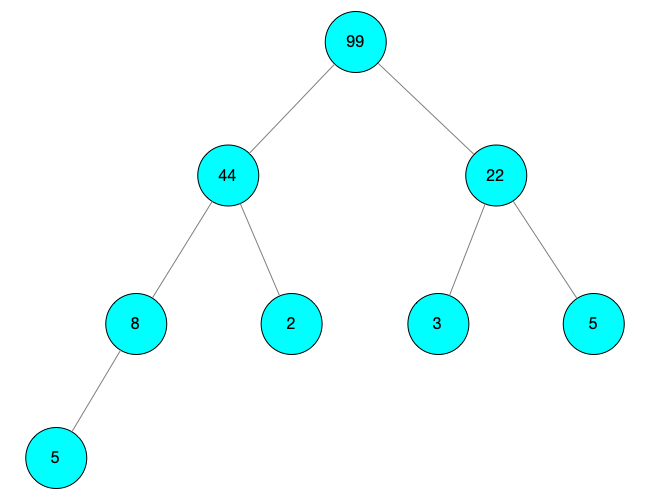
此時(shí) child 沒有孩子節(jié)點(diǎn),停止深度調(diào)整 最終得到大根堆如下圖所示

用數(shù)組進(jìn)行表示則為:[99, 44, 22, 8, 2, 3, 5, 5]
代碼
/**
* 此代碼建議 mock 數(shù)據(jù),并將其繪制成完美二叉樹,參照二叉樹進(jìn)行閱讀
*/
function buildHeap(data){
let len = data.length
// 從最后一個(gè)根節(jié)點(diǎn)開始,向前遍歷所有根節(jié)點(diǎn)
// 取 len / 2 作為 i 的初始值,是因?yàn)樽詈笠粋€(gè)孩子節(jié)點(diǎn)是 len - 1
// 它可能是左孩子也可能是右孩子,那么可以根據(jù)公式算出對(duì)應(yīng)的根節(jié)點(diǎn)
// 它一定在 len / 2 附近,且小于 len / 2
for(let i = Math.floor(len / 2); i >= 0; i --){
heapAjust(data, i, len);
}
}
/**
* 調(diào)整操作
* 根據(jù)傳入的數(shù)據(jù)調(diào)整二叉樹
* i 為根節(jié)點(diǎn)的 key
* len 為需調(diào)整數(shù)據(jù)的長(zhǎng)度
*/
function heapAjust(data, i, len){
// 尋找 i 的左孩子
let child = 2 * i + 1
// 如果 child 大于 len 說明 i 不是根節(jié)點(diǎn)
while(child < len) {
// 比較兩個(gè)孩子節(jié)點(diǎn),將 child 指向大的那個(gè)
if(child + 1 <= len && data[child] < data[child + 1]){
child = child + 1
}
// 如果孩子節(jié)點(diǎn)比根節(jié)點(diǎn)大,兩個(gè)節(jié)點(diǎn)互換
if(data[i] < data[child]){
let temp = data[i]
data[i] = data[child]
data[child] = temp
// 互換之后將被更新的孩子節(jié)點(diǎn)繼續(xù)作為根節(jié)點(diǎn),進(jìn)行深度查找
i = child
child = 2 * i + 1
}
else {
break
}
}
}
堆排序
思路
先將整個(gè)數(shù)組調(diào)整成大根堆 則數(shù)組的第一個(gè)元素最大,將其與數(shù)組最后一個(gè)元素替換,此時(shí)大根堆被破壞 重新調(diào)整前 length - 1 個(gè)元素,將它們調(diào)整成新的大根堆 以此循環(huán),直到堆中的元素只有一個(gè)時(shí)
代碼
var arraySort = function(arr) {
// 將數(shù)組調(diào)整成大根堆
buildHeap(arr);
// 下面需要注意的時(shí)候參數(shù)的邊界
for(let i = arr.length - 1; i >= 0; i --) {
// 互換數(shù)據(jù)
let temp = arr[i]
arr[i] = arr[0]
arr[0] = temp
// 將前面的元素重新調(diào)整成大根堆
heapAjust(arr, 0, i-1);
}
}
總結(jié)
堆排序是不穩(wěn)定的 在尋找前幾個(gè)值最大的場(chǎng)景中比較好用

回復(fù)“加群”與大佬們一起交流學(xué)習(xí)~
點(diǎn)擊“閱讀原文”查看 100+ 篇原創(chuàng)文章
評(píng)論
圖片
表情
