MIT新研究：過去80年，算法效率提升到底有多快？

---

  新智元報(bào)道  

來源：MIT

編輯：David

提起算法，它有點(diǎn)像計(jì)算機(jī)的父母，它會(huì)告訴計(jì)算機(jī)如何理解信息，而計(jì)算機(jī)反過來可以從算法中獲得有用的東西。

算法的效率越高，計(jì)算機(jī)要做的工作就越少。對于計(jì)算機(jī)硬件的所有技術(shù)進(jìn)步，以及備受爭議的摩爾定律的壽命問題來說，計(jì)算機(jī)硬件的性能只是問題的一方面。

而問題另一方面則在硬件之外：算法的效率問題。如果算法的效率提升了，對同一計(jì)算任務(wù)需要的算力就會(huì)降低。

雖然算法效率問題可能不太受關(guān)注，但你是否注意到，經(jīng)常使用的搜索引擎是否突然變快了十分之一，而在大型數(shù)據(jù)集中活動(dòng)，就感覺就像在泥濘中跋涉一樣艱難緩慢。

這些都與算法效率有關(guān)。

近日，麻省理工學(xué)院計(jì)算機(jī)科學(xué)與人工智能實(shí)驗(yàn)室 (CSAIL) 的科學(xué)家提出疑問：算法效率的提升速度到底有多快？

關(guān)于這個(gè)問題，現(xiàn)有數(shù)據(jù)大部分是敘事性的，其中很大一部分是面向特定算法的案例研究，再把這些研究結(jié)果加以推廣。

面對實(shí)證研究數(shù)據(jù)的不足，研究團(tuán)隊(duì)主要利用了來自 57 部教科書和 1110 多篇研究論文的數(shù)據(jù)，以追溯算法效率提升的歷史。

其中有些論文的結(jié)論中直接給出了新的算法有多高效，有的論文則需要作者使用“偽代碼”（對算法基本細(xì)節(jié)的簡單描述）進(jìn)行重構(gòu)。

研究人員總共研究了 113 個(gè)“算法系”，即解決計(jì)算機(jī)科學(xué)教科書中最重要的同一問題的算法集。他們對每個(gè)算法族的歷史進(jìn)行了回顧，跟蹤每次針對某一問題提出的新算法，并特別注意更高效的算法。

圖1 算法發(fā)現(xiàn)和改進(jìn)。(a) 每十年發(fā)現(xiàn)的新算法系的數(shù)量。(b) 已知算法系的比例每十年都有所提高。(c) 首次發(fā)現(xiàn)時(shí)算法系的漸近時(shí)間復(fù)雜度分類。(d) 同一時(shí)間復(fù)雜度的算法轉(zhuǎn)換到另一個(gè)時(shí)間復(fù)雜度的每年平均概率（反應(yīng)算法系復(fù)雜度提升的平均水平）。在（c）和（d）中“>n3”的時(shí)間復(fù)雜度表示超過多項(xiàng)式級，但不到指數(shù)級。

最早的算法系可追溯到上世紀(jì)40年代，每個(gè)算法系平均有 8 個(gè)算法，按時(shí)間順序效率逐步提升。為了共享這一發(fā)現(xiàn)，團(tuán)隊(duì)還創(chuàng)建了“算法維基”頁面（Algorithm-Wiki.org）。

研究人員繪制了圖表，標(biāo)識這些算法族效率提升的速度，重點(diǎn)關(guān)注算法分析最多的特征——這些特征往往決定了解決問題的速度有多快（用計(jì)算機(jī)術(shù)語說，就是“最壞情況下的時(shí)間復(fù)雜度”）。

圖 2 算法系的相對效率提升，使用漸近時(shí)間復(fù)雜度的變化計(jì)算。參考線是SPECInt 基準(zhǔn)性能。(a) 與該系列中的第一個(gè)算法（n = 100 萬）相比，四個(gè)算法系的歷史改進(jìn)。(b) 算法改進(jìn)對“最近鄰搜索”算法系列的輸入大小 (n)的敏感度。為了便于比較算法改進(jìn)效果隨時(shí)間的變化，在圖(b) 中將算法系和硬件基準(zhǔn)的起始時(shí)間段對齊。

結(jié)果顯示，變數(shù)很大，但也發(fā)現(xiàn)了關(guān)于計(jì)算機(jī)科學(xué)變革性算法效率提升的重要信息。即：

• 對于大型計(jì)算問題，43% 的算法系的效率提升帶來的收益，不低于摩爾定律帶來的收益。

   

• 在 14% 的問題中，算法效率提升的收益遠(yuǎn)超硬件性能提升的收益。

   

• 對于大數(shù)據(jù)問題，算法效率提升收益特別大，因此近年來，這一效果與摩爾定律相比越來越明顯。

當(dāng)算法系從指數(shù)復(fù)雜度過渡到多項(xiàng)式復(fù)雜度時(shí)，情況出現(xiàn)了最大的變化。

所謂指數(shù)復(fù)雜度算法，就像一個(gè)人猜密碼鎖的密碼一樣。如果密碼盤上只有一位數(shù)，那么任務(wù)很簡單。如果像自行車鎖一樣，表盤是4位數(shù)，估計(jì)你的自行車很難有人偷得走，但仍然可以一個(gè)個(gè)試。如果是表盤是50位的，就幾乎不可能破解了，需要的步驟太多了。

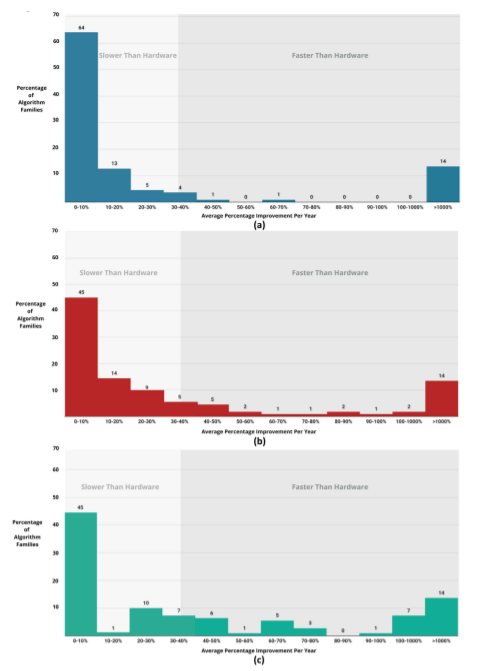
圖3 基于漸近時(shí)間復(fù)雜度計(jì)算的110個(gè)算法系效率提升的年平均速度分布，其中問題規(guī)模為：(a) n = 1000，(b) n = 100萬，(c) n = 10億。硬件性能提升線表示從 1978 年到 2017 年，SPECInt 基準(zhǔn)性能的平均年增長率

這類問題也是計(jì)算機(jī)面對的難題，隨著問題的規(guī)模越來越大，很快就會(huì)超過計(jì)算機(jī)的處理能力，這個(gè)問題光靠摩爾定律是解決不了的。

解決之道在于找到多項(xiàng)式復(fù)雜度的算法。

研究人員表示，隨著摩爾定律終結(jié)這個(gè)話題越來越多地被提及，我們需要將未來的解決方案的重點(diǎn)放在算法的效率提升上。

圖4 前導(dǎo)常數(shù)在算法性能提升中的重要性評價(jià)

研究結(jié)果表明，從歷史上看，算法效率的提升帶來的收益是巨大的。不過二者之間存在著頻度的差異，摩爾定律帶來的提升是平滑而緩慢的，而算法效率的提升是階梯式的躍進(jìn)，但出現(xiàn)沒那么頻繁。

本文通訊作者尼爾·湯普森說：

這是業(yè)界第一篇說明算法效率提升速度的論文。通過我們的分析，可以得出算法改進(jìn)后，使用同樣的算力可以完成多少任務(wù)。

隨著問題的規(guī)模不斷增大，比如達(dá)到數(shù)十億或數(shù)萬億個(gè)數(shù)據(jù)點(diǎn)，算法效率的提升帶來的收益，比硬件性能的提升更重要，而且重要得多。

在我們開始逐步為算力不足發(fā)愁的時(shí)代，在摩爾定律越來越顯出疲態(tài)的今天，這一發(fā)現(xiàn)可能為未來解決超大型計(jì)算問題開辟一條新的思路。

參考鏈接：

https://news.mit.edu/2021/how-quickly-do-algorithms-improve-0920

https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9540991