機(jī)器學(xué)習(xí)中，大部分是分類問題，另一種常見的機(jī)器學(xué)習(xí)問題是回歸問題，它預(yù)測(cè)一個(gè)連續(xù)值而不是離散的標(biāo)簽，例如，根據(jù)氣象數(shù)據(jù)預(yù)測(cè)明天的氣溫，或者根據(jù)軟件說明書預(yù)測(cè)完成軟件項(xiàng)目所需要的時(shí)間、根據(jù)消費(fèi)行為預(yù)測(cè)用戶的年齡等，今天的案例就是根據(jù)周邊的數(shù)據(jù)，預(yù)測(cè)房價(jià)，房價(jià)是一系列的連續(xù)值，因此是一個(gè)典型的回歸問題。

注意：不要將回歸問題與 logistic 回歸算法混為一談。令人困惑的是，logistic 回歸不是回歸算法，而是分類算法。

一、波士頓房價(jià)數(shù)據(jù)集

本節(jié)將要預(yù)測(cè) 20 世紀(jì) 70 年代中期波士頓郊區(qū)房屋價(jià)格的中位數(shù)，已知當(dāng)時(shí)郊區(qū)的一些數(shù)據(jù)點(diǎn)，比如犯罪率、當(dāng)?shù)胤慨a(chǎn)稅率等。本節(jié)用到的數(shù)據(jù)集與前面兩個(gè)例子有一個(gè)有趣的區(qū)別。

它包含的數(shù)據(jù)點(diǎn)相對(duì)較少，只有 506 個(gè)，分為 404 個(gè)訓(xùn)練樣本和 102 個(gè)測(cè)試樣本。輸入數(shù)據(jù)的每個(gè)特征（比如犯罪率）都有不同的取值范圍。例如，有些特性是比例，取值范圍為 0~1；有的取值范圍為 1~12；還有的取值范圍為 0~100，等等。

加載波士頓房價(jià)數(shù)據(jù)

from keras.datasets import boston_housing(train_data,train_targets),(test_data,test_targets)?=?boston_housing.load_data()

我們來看一下數(shù)據(jù)。

train_data.shape (404, 13) test_data.shape (102, 13)

如你所見，我們有 404 個(gè)訓(xùn)練樣本和 102 個(gè)測(cè)試樣本，每個(gè)樣本都有 13 個(gè)數(shù)值特征，比如人均犯罪率、每個(gè)住宅的平均房間數(shù)、高速公路可達(dá)性等。目標(biāo)是房屋價(jià)格的中位數(shù)，單位是千美元。

train_targetsarray([15.2, 42.3, 50. , 21.1, 17.7, 18.5, 11.3, 15.6, 15.6, 14.4, 12.1,17.9, 23.1, ......

房價(jià)大都在 10 000~50 000 美元。折合人民幣6.5w-40w一平米，如果你覺得這很便宜，不要忘記當(dāng)時(shí)是 20 世紀(jì)70年代中期，而且這些價(jià)格沒有根據(jù)通貨膨脹進(jìn)行調(diào)整。所以一線城市的房價(jià)，還大有上漲空間

二、準(zhǔn)備數(shù)據(jù)

將取值范圍差異很大的數(shù)據(jù)輸入到神經(jīng)網(wǎng)絡(luò)中，這是有問題的。網(wǎng)絡(luò)可能會(huì)自動(dòng)適應(yīng)這種取值范圍不同的數(shù)據(jù)，但學(xué)習(xí)肯定變得更加困難。對(duì)于這種數(shù)據(jù)，普遍采用的最佳實(shí)踐是對(duì)每個(gè)特征做標(biāo)準(zhǔn)化，即對(duì)于輸入數(shù)據(jù)的每個(gè)特征（輸入數(shù)據(jù)矩陣中的列），減去特征平均值，再除以標(biāo)準(zhǔn)差，這樣得到的特征平均值為 0，標(biāo)準(zhǔn)差為 1。用 Numpy 可以很容易實(shí)現(xiàn)標(biāo)準(zhǔn)化。

# 數(shù)據(jù)歸一化mean = train_data.mean(axis = 0)train_data -= meanstd = train_data.std(axis = 0)train_data?/=?stdtest_data -= meantest_data /= std

?注意：用于測(cè)試數(shù)據(jù)標(biāo)準(zhǔn)化的均值和標(biāo)準(zhǔn)差都是在訓(xùn)練數(shù)據(jù)上計(jì)算得到的。在工作流程中，你不能使用在測(cè)試數(shù)據(jù)上計(jì)算得到的任何結(jié)果，即使是像數(shù)據(jù)標(biāo)準(zhǔn)化這么簡單的事情也不行。

?

三、構(gòu)建模型框架

由于樣本數(shù)量很少，我們將使用一個(gè)非常小的網(wǎng)絡(luò)，其中包含兩個(gè)隱藏層，每層有 64 個(gè)單元。一般來說，訓(xùn)練數(shù)據(jù)越少，過擬合會(huì)越嚴(yán)重，而較小的網(wǎng)絡(luò)可以降低過擬合。

#構(gòu)建模型框架from keras import layers from?keras?import?modelsdef build_model():    model = models.Sequential()    model.add(layers.Dense(64,activation='relu',input_shape=(train_data.shape[1],)))    model.add(layers.Dense(64,activation='relu'))    model.add(layers.Dense(1))    model.compile(optimizer='rmsprop',loss='mse',metrics=['mae'])    return model

網(wǎng)絡(luò)的最后一層只有一個(gè)單元，沒有激活，是一個(gè)線性層。這是標(biāo)量回歸（標(biāo)量回歸是預(yù)測(cè)單一連續(xù)值的回歸）的典型設(shè)置。添加激活函數(shù)將會(huì)限制輸出范圍。例如，如果向最后一層添加 sigmoid 激活函數(shù)，網(wǎng)絡(luò)只能學(xué)會(huì)預(yù)測(cè) 0~1 范圍內(nèi)的值。這里最后一層是純線性的，所以網(wǎng)絡(luò)可以學(xué)會(huì)預(yù)測(cè)任意范圍內(nèi)的值。

注意，編譯網(wǎng)絡(luò)用的是 mse 損失函數(shù)，即均方誤差（MSE，mean squared error），預(yù)測(cè)值與目標(biāo)值之差的平方。這是回歸問題常用的損失函數(shù)。

在訓(xùn)練過程中還監(jiān)控一個(gè)新指標(biāo)：平均絕對(duì)誤差（MAE，mean absolute error）。它是預(yù)測(cè)值與目標(biāo)值之差的絕對(duì)值。比如，如果這個(gè)問題的 MAE 等于 0.5，就表示你預(yù)測(cè)的房價(jià)與實(shí)際價(jià)格平均相差 500 美元。

四、利用K 折驗(yàn)證來驗(yàn)證你的方法

為了在調(diào)節(jié)網(wǎng)絡(luò)參數(shù)（比如訓(xùn)練的輪數(shù)）的同時(shí)對(duì)網(wǎng)絡(luò)進(jìn)行評(píng)估，你可以將數(shù)據(jù)劃分為訓(xùn)練集和驗(yàn)證集，正如前面例子中所做的那樣。但由于數(shù)據(jù)點(diǎn)很少，驗(yàn)證集會(huì)非常小（比如大約100 個(gè)樣本）。因此，驗(yàn)證分?jǐn)?shù)可能會(huì)有很大波動(dòng)，這取決于你所選擇的驗(yàn)證集和訓(xùn)練集。也就是說，驗(yàn)證集的劃分方式可能會(huì)造成驗(yàn)證分?jǐn)?shù)上有很大的方差，這樣就無法對(duì)模型進(jìn)行可靠的評(píng)估。

在這種情況下，最佳做法是使用 K 折交叉驗(yàn)證（見圖 3-11）。這種方法將可用數(shù)據(jù)劃分為 K個(gè)分區(qū)（K 通常取 4 或 5），實(shí)例化 K 個(gè)相同的模型，將每個(gè)模型在 K-1 個(gè)分區(qū)上訓(xùn)練，并在剩下的一個(gè)分區(qū)上進(jìn)行評(píng)估。模型的驗(yàn)證分?jǐn)?shù)等于 K 個(gè)驗(yàn)證分?jǐn)?shù)的平均值。這種方法的代碼實(shí)現(xiàn)很簡單。

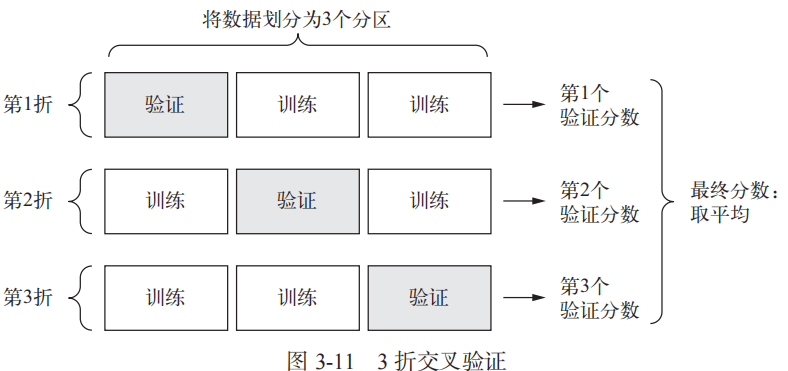
import keras import numpy as np #K折交叉驗(yàn)證k   = 5num = len(train_data)//kall_score = []for i in range(k):    X_val = train_data[i*num:(i+1)*num]    Y_val = train_targets[i*num:(i+1)*num]    X_train = np.concatenate([train_data[:i*num],train_data[(i+1)*num:]],axis=0)    Y_train = np.concatenate([train_targets[:i*num],train_targets[(i+1)*num:]],axis=0)    model = build_model()    model.fit(X_train,Y_train,epochs=100,batch_size=1,verbose=1)    val_mse,val_mae = model.evaluate(X_val,Y_val,verbose=0)    all_score.append(val_mae)

運(yùn)行結(jié)果如下，取平均，基本上就是模型能到達(dá)的最小誤差了

all_score[1.9652233123779297,2.5989739894866943,1.9110896587371826,2.5641400814056396, 2.337777853012085]
np.mean(all_score) 2.275440979003906

每次運(yùn)行模型得到的驗(yàn)證分?jǐn)?shù)有很大差異，從 1.9 到 2.6 不等。平均分?jǐn)?shù)（2.27）是比單一分?jǐn)?shù)更可靠的指標(biāo)——這就是 K 折交叉驗(yàn)證的關(guān)鍵。在這個(gè)例子中，預(yù)測(cè)的房價(jià)與實(shí)際價(jià)格平均相差 2200 美元，考慮到實(shí)際價(jià)格范圍在 10 000~50 000 美元，這一差別還是很大的。我們讓訓(xùn)練時(shí)間更長一點(diǎn)，達(dá)到 500 個(gè)輪次。為了記錄模型在每輪的表現(xiàn)，我們需要修改訓(xùn)練循環(huán)，以保存每輪的驗(yàn)證分?jǐn)?shù)記錄。

五、模型最后評(píng)估

完成模型調(diào)參之后（除了輪數(shù)，還可以調(diào)節(jié)隱藏層大小），你可以使用最佳參數(shù)在所有訓(xùn)練數(shù)據(jù)上訓(xùn)練最終的生產(chǎn)模型，然后觀察模型在測(cè)試集上的性能。

model = build_model()model.fit(train_data,train_targets,epochs=100,batch_size=1,verbose=1)test_mse,test_mae = model.evaluate(test_data,test_targets,verbose=0)
test_mae2.213838815689087
#如果要看預(yù)測(cè)的明細(xì)結(jié)果model.predict(test_data)array([[18.471083],       [20.257647],       [33.627922],       [23.181114],       [23.600664],       [29.277847],       [21.298449],       [17.50559 ],       [21.228243]], dtype=float32)