機(jī)器學(xué)習(xí)最全知識(shí)點(diǎn)匯總
點(diǎn)擊下方卡片,關(guān)注“新機(jī)器視覺”公眾號(hào)
重磅干貨,第一時(shí)間送達(dá)

1.列舉常用的最優(yōu)化方法
梯度下降法
牛頓法,
擬牛頓法
坐標(biāo)下降法
梯度下降法的改進(jìn)型如AdaDelta,AdaGrad,Adam,NAG等。?
2.梯度下降法的關(guān)鍵點(diǎn)
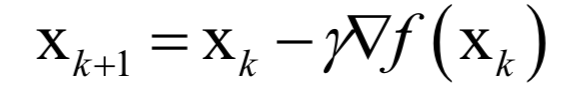
3.牛頓法的關(guān)鍵點(diǎn)
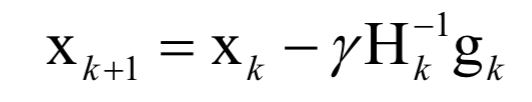
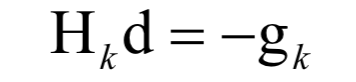
4.拉格朗日乘數(shù)法
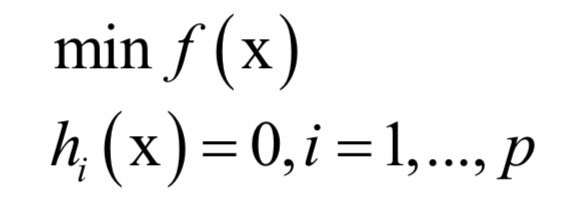

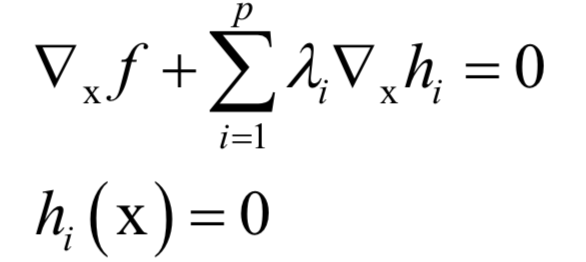
主成分分析
線性判別分析
流形學(xué)習(xí)中的拉普拉斯特征映射
隱馬爾科夫模型
5.凸優(yōu)化
優(yōu)化變量的可行域是一個(gè)凸集
目標(biāo)函數(shù)是一個(gè)凸函數(shù)
線性回歸
嶺回歸
LASSO回歸
Logistic回歸
支持向量機(jī)
Softamx回歸
6.拉格朗日對(duì)偶
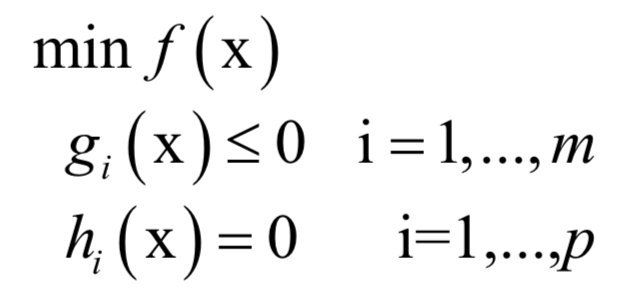
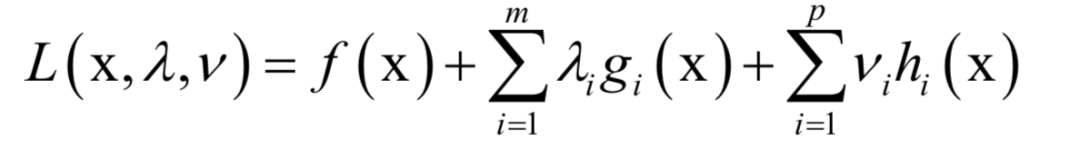
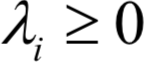 的約束。原問(wèn)題為:
的約束。原問(wèn)題為: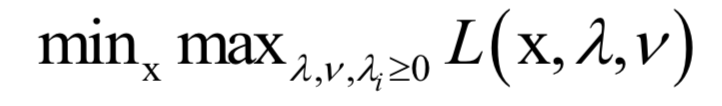
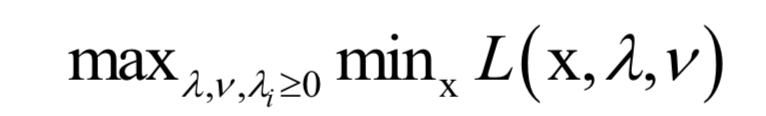
7.KKT條件
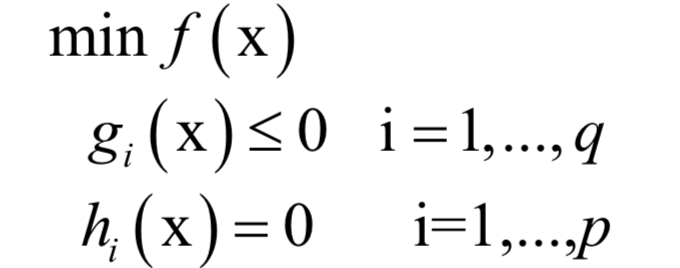

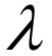 和
和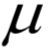 稱為KKT乘子。在最優(yōu)解處
稱為KKT乘子。在最優(yōu)解處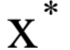 應(yīng)該滿足如下條件:
應(yīng)該滿足如下條件:
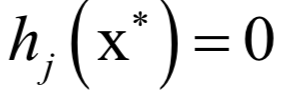
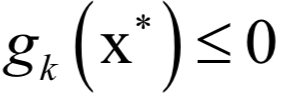
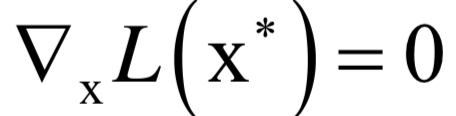 和之前的拉格朗日乘數(shù)法一樣。唯一多了關(guān)于gi?(x)的條件:
和之前的拉格朗日乘數(shù)法一樣。唯一多了關(guān)于gi?(x)的條件: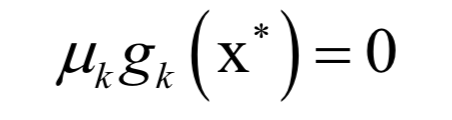
8.特征值與特征向量
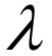 和一個(gè)非0向量X,滿足:
和一個(gè)非0向量X,滿足: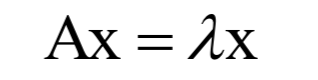
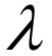 為矩陣A的特征值,X為該特征值對(duì)應(yīng)的特征向量。根據(jù)上面的定義有下面線性方程組
為矩陣A的特征值,X為該特征值對(duì)應(yīng)的特征向量。根據(jù)上面的定義有下面線性方程組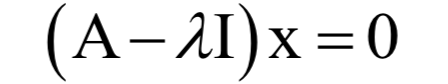
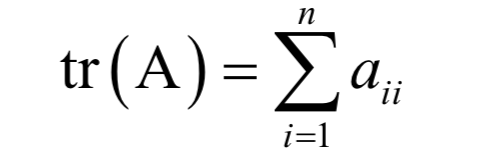
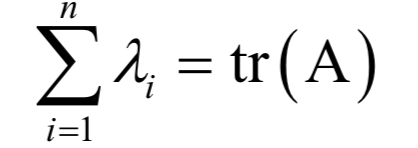
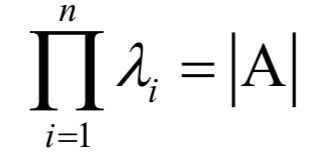
9.奇異值分解
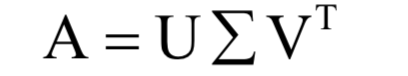
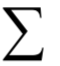 為m x n的對(duì)角矩陣,除了主對(duì)角線
為m x n的對(duì)角矩陣,除了主對(duì)角線10.最大似然估計(jì)
 ,確定這些參數(shù)常用的一種方法是最大似然估計(jì)。
,確定這些參數(shù)常用的一種方法是最大似然估計(jì)。 。最大似然估計(jì)的直觀解釋是,尋求一組參數(shù),使得給定的樣本集出現(xiàn)的概率最大。
。最大似然估計(jì)的直觀解釋是,尋求一組參數(shù),使得給定的樣本集出現(xiàn)的概率最大。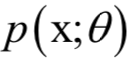 ,其中X為隨機(jī)變量,
,其中X為隨機(jī)變量, 為要估計(jì)的參數(shù)。給定一組樣本xi,i?=1,...,l,它們都服從這種分布,并且相互獨(dú)立。最大似然估計(jì)構(gòu)造如下似然函數(shù):
為要估計(jì)的參數(shù)。給定一組樣本xi,i?=1,...,l,它們都服從這種分布,并且相互獨(dú)立。最大似然估計(jì)構(gòu)造如下似然函數(shù):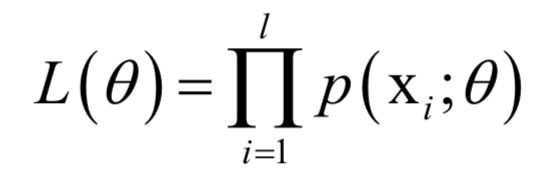
 的函數(shù),我們要讓該函數(shù)的值最大化,這樣做的依據(jù)是這組樣本發(fā)生了,因此應(yīng)該最大化它們發(fā)生的概率,即似然函數(shù)。這就是求解如下最優(yōu)化問(wèn)題:
的函數(shù),我們要讓該函數(shù)的值最大化,這樣做的依據(jù)是這組樣本發(fā)生了,因此應(yīng)該最大化它們發(fā)生的概率,即似然函數(shù)。這就是求解如下最優(yōu)化問(wèn)題:
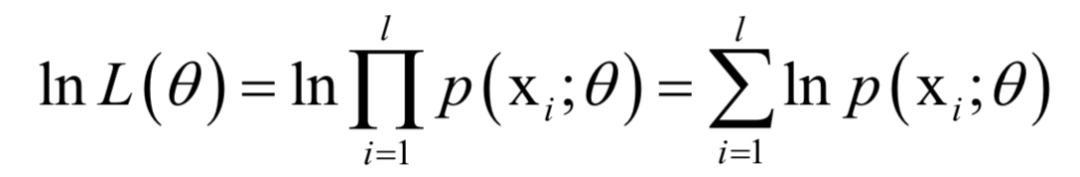
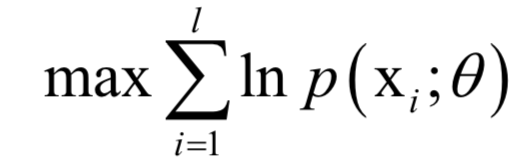
基本概念
1.有監(jiān)督學(xué)習(xí)與無(wú)監(jiān)督學(xué)習(xí)
2.分類問(wèn)題與回歸問(wèn)題
3.生成模型與判別模型
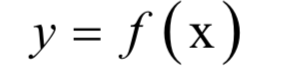
4.交叉驗(yàn)證
5.過(guò)擬合與欠擬合
6.偏差與方差分解
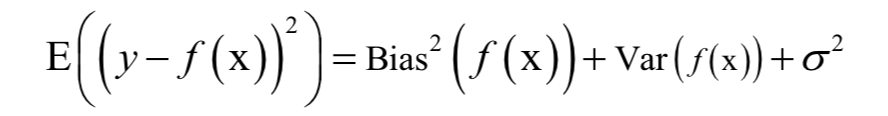
7.正則化
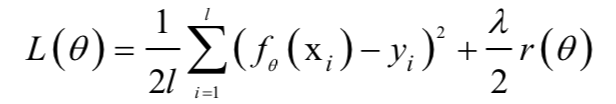
8.維數(shù)災(zāi)難
貝葉斯分類器
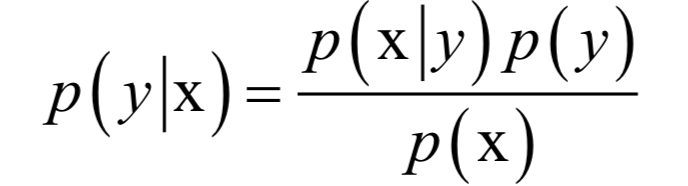
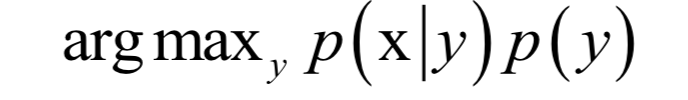
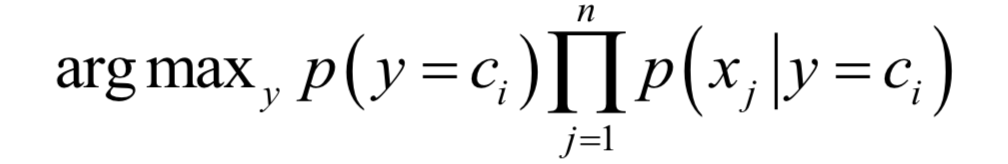
決策樹
1.用樣本集D建立根節(jié)點(diǎn),找到一個(gè)判定規(guī)則,將樣本集分裂成D1和D2兩部分,同時(shí)為根節(jié)點(diǎn)設(shè)置判定規(guī)則。
2.用樣本集D1遞歸建立左子樹。
3.用樣本集D2遞歸建立右子樹。
4.如果不能再進(jìn)行分裂,則把節(jié)點(diǎn)標(biāo)記為葉子節(jié)點(diǎn),同時(shí)為它賦值。
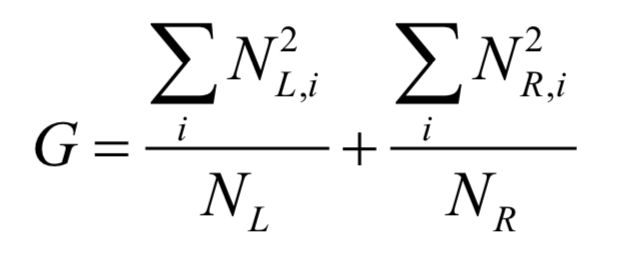
隨機(jī)森林
AdaBoost算法
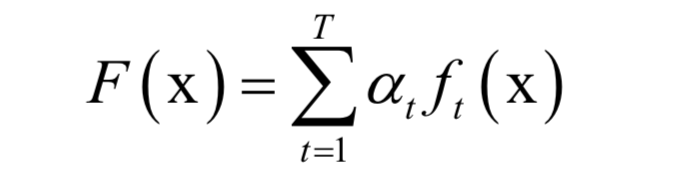


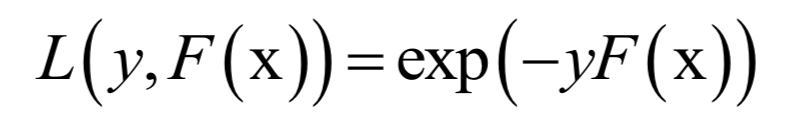
主成分分析

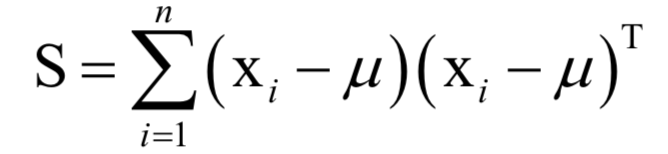
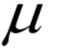 為所有樣本的均值向量。則上面的重構(gòu)誤差最小化等價(jià)于求解如下問(wèn)題:
為所有樣本的均值向量。則上面的重構(gòu)誤差最小化等價(jià)于求解如下問(wèn)題: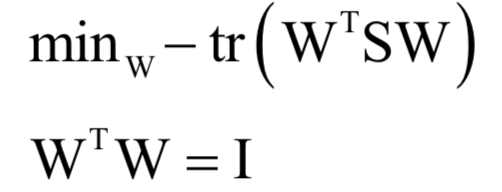
線性判別分析
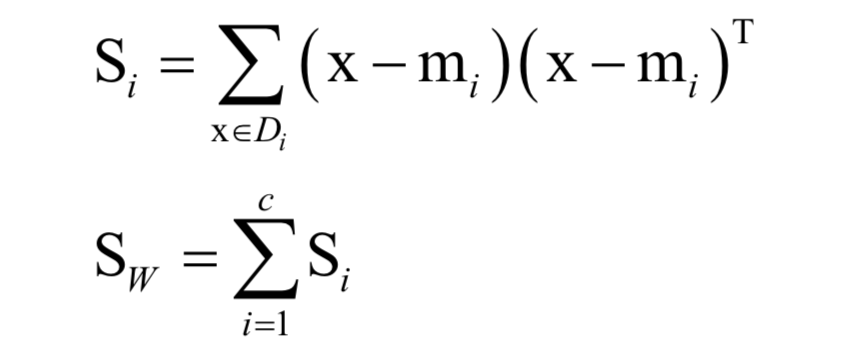
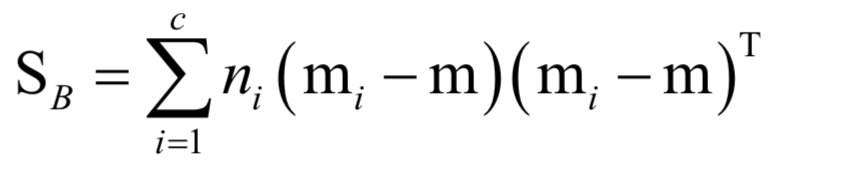
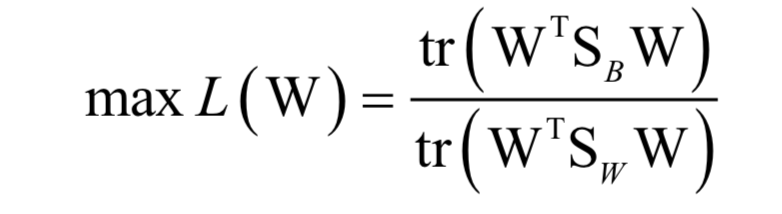
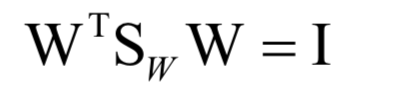
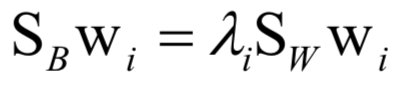
kNN算法
人工神經(jīng)網(wǎng)絡(luò)

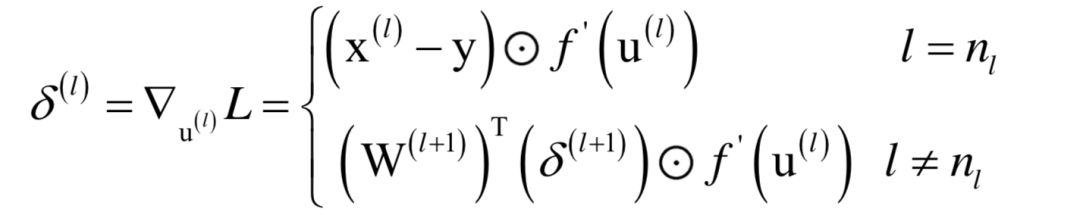
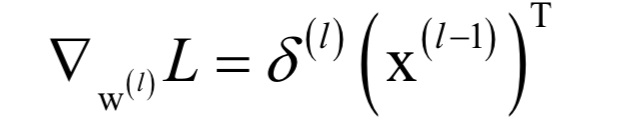
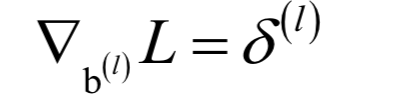
支持向量機(jī)


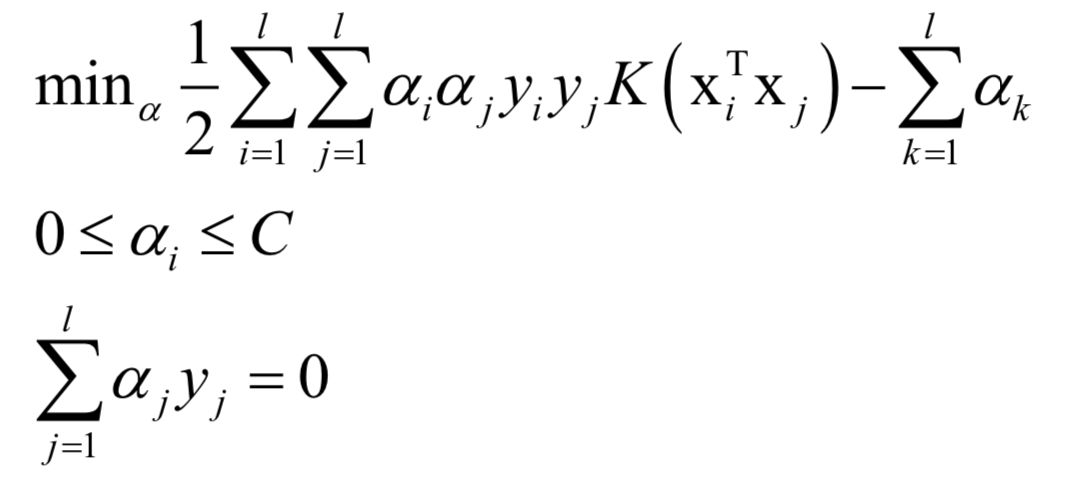

logistic回歸
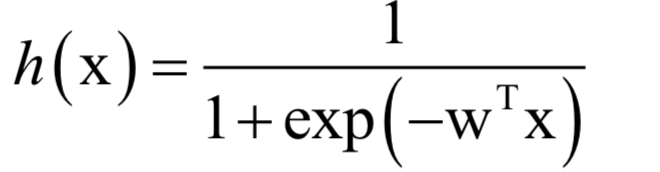
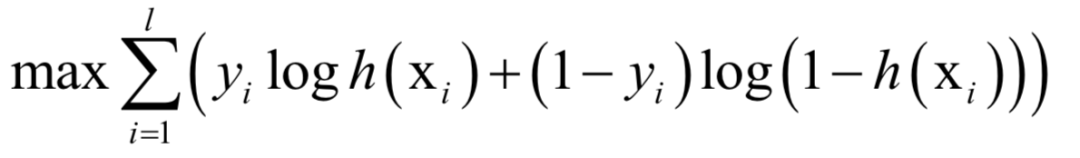
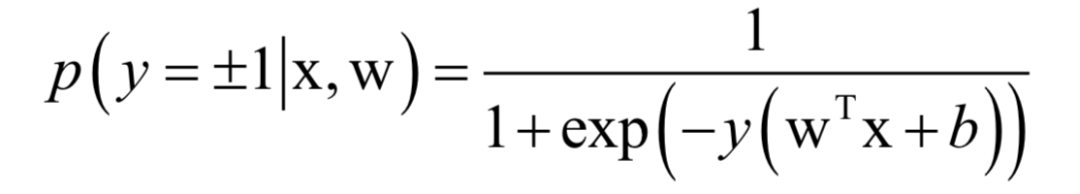

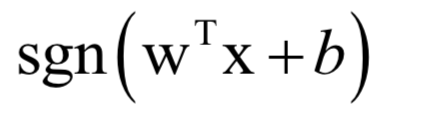
K均值算法
卷積神經(jīng)網(wǎng)絡(luò)
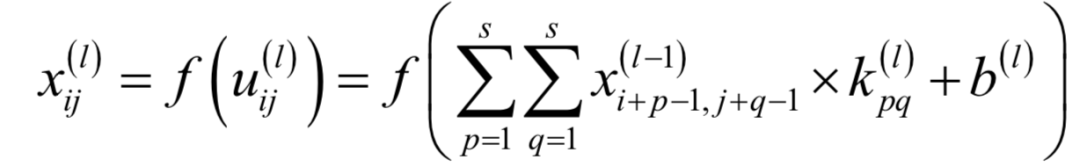
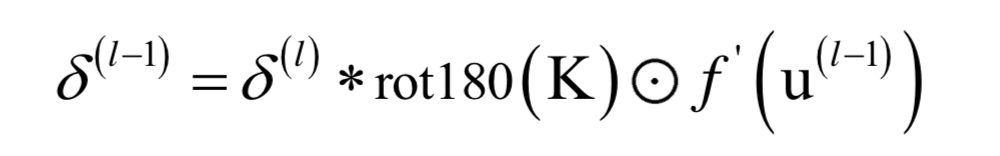
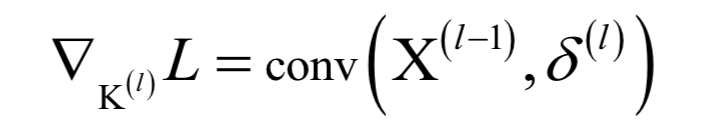
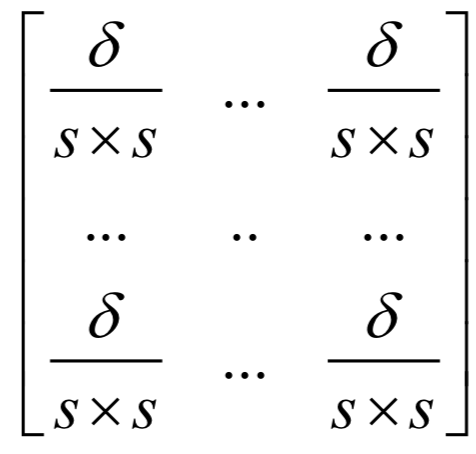
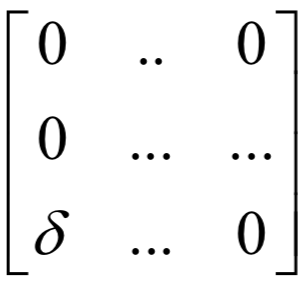
循環(huán)神經(jīng)網(wǎng)絡(luò)
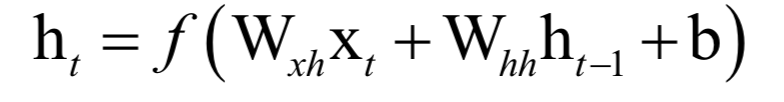
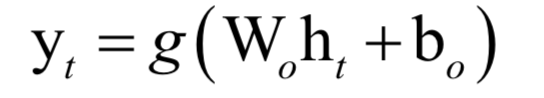
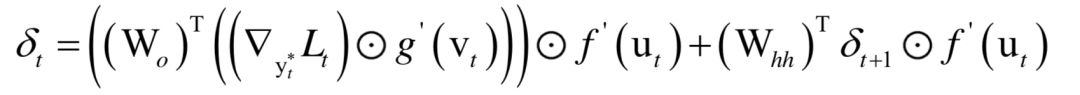
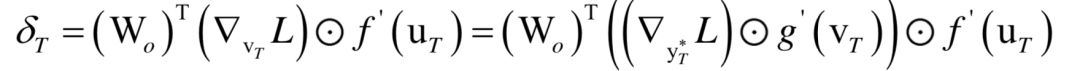
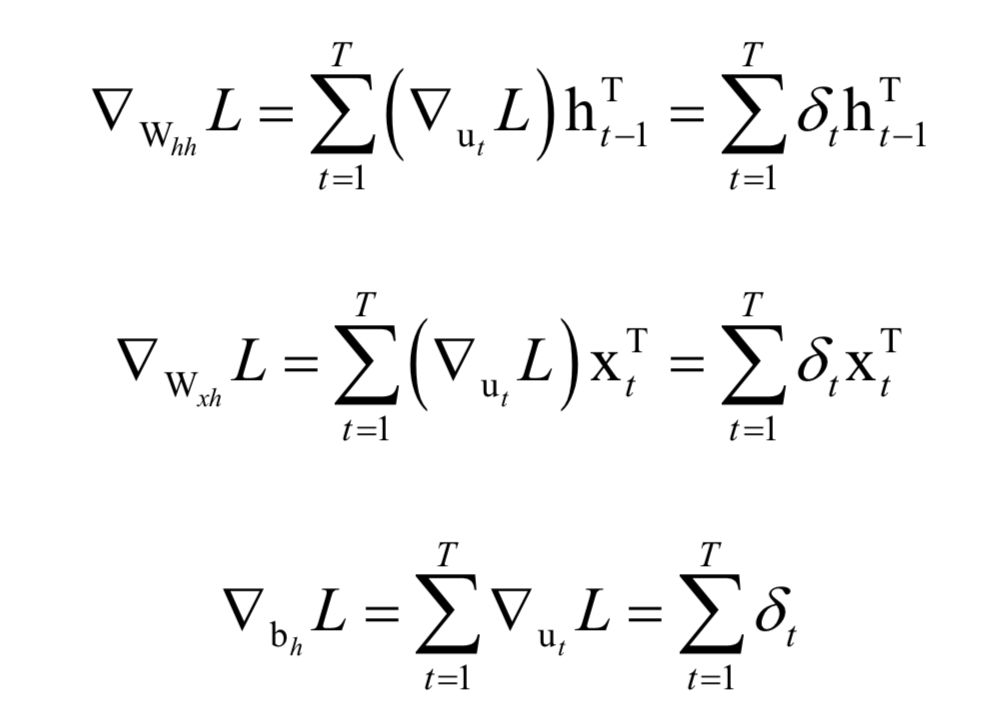
高斯混合模型
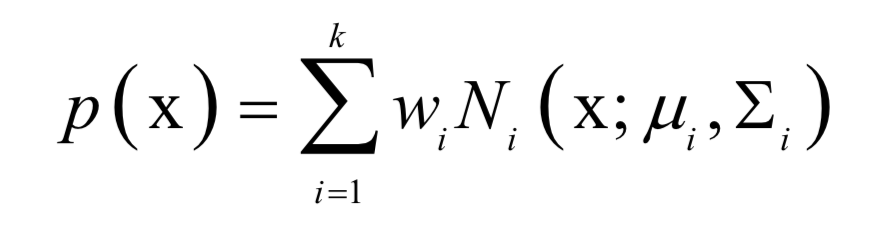
 為高斯分布的均值向量,
為高斯分布的均值向量,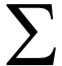 為協(xié)方差矩陣。所有權(quán)重之和為1,即:
為協(xié)方差矩陣。所有權(quán)重之和為1,即: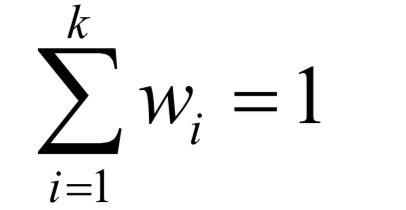
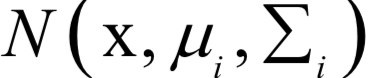 產(chǎn)生出這個(gè)樣本數(shù)據(jù)x。高斯混合模型可以逼近任何一個(gè)連續(xù)的概率分布,因此它可以看做是連續(xù)性概率分布的萬(wàn)能逼近器。之所有要保證權(quán)重的和為1,是因?yàn)楦怕拭芏群瘮?shù)必須滿足在
產(chǎn)生出這個(gè)樣本數(shù)據(jù)x。高斯混合模型可以逼近任何一個(gè)連續(xù)的概率分布,因此它可以看做是連續(xù)性概率分布的萬(wàn)能逼近器。之所有要保證權(quán)重的和為1,是因?yàn)楦怕拭芏群瘮?shù)必須滿足在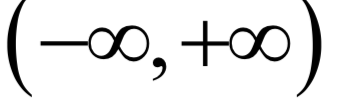 內(nèi)的積分值為1。
內(nèi)的積分值為1。EM算法
 的值,接下來(lái)循環(huán)迭代,每次迭代時(shí)分為兩步:
的值,接下來(lái)循環(huán)迭代,每次迭代時(shí)分為兩步: ,計(jì)算在給定x時(shí)對(duì)z的條件概率的數(shù)學(xué)期望:
,計(jì)算在給定x時(shí)對(duì)z的條件概率的數(shù)學(xué)期望:
 的值:
的值: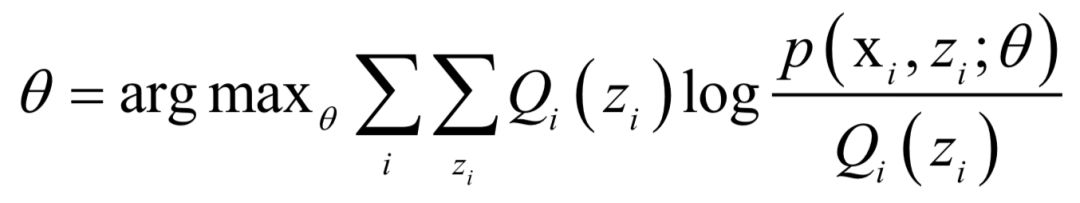

本文僅做學(xué)術(shù)分享,如有侵權(quán),請(qǐng)聯(lián)系刪文。
