計算機視覺方向簡介 | 半全局匹配SGM
點擊上方“小白學(xué)視覺”,選擇加"星標"或“置頂”
重磅干貨,第一時間送達
前言
目標讀者:對密集匹配,三維重建等有基本概念并感興趣的人群。 文章及代碼資源:
導(dǎo)讀:
SGM雖然名字上稱為半全局匹配,但實際上還是采用的全局匹配算法中最優(yōu)化能量函數(shù)的思想,即尋找每個像素的最優(yōu)視差來使得整張影像的全局能量函數(shù)最小,下式為SGM所采用的能量函數(shù):

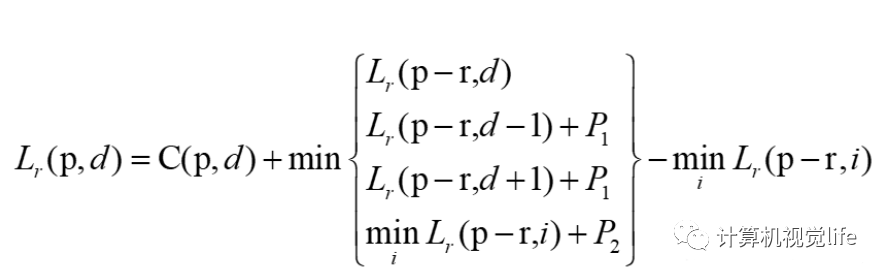
struct path {
short rowDiff;
short colDiff;
short index;
};
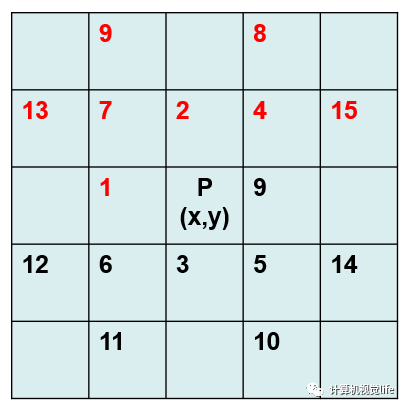
在視差計算之前,首先需要定義大小為W×H×D(W為影像寬度,H為影像高度,D則為事先給定的視差范圍)的三維矩陣C來存儲每個像素在視差范圍內(nèi)每個視差下的匹配代價值。矩陣C通常稱為DSI(Disparity Space Image),這個長方塊也是我們常說的視差空間。下圖為DSI的示意圖:
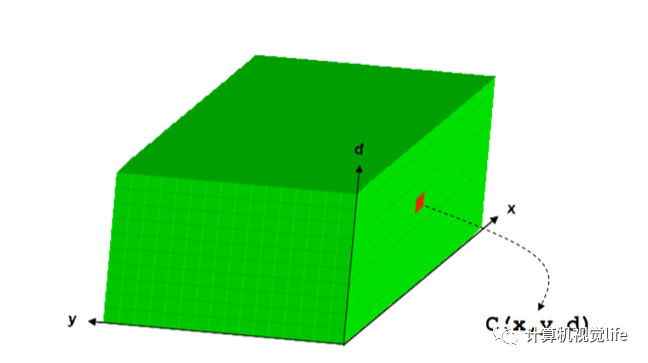
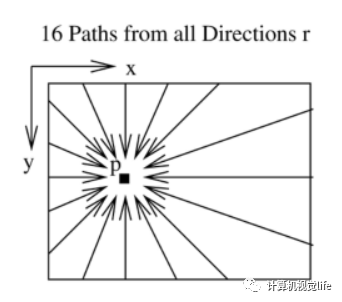
感性上來講,SGM能夠揚名的一個很重要的點就是它將一個NP的全局優(yōu)化問題簡化成了一個多方向的代價問題,即用多個一維路徑代價聚合的方式來近似二維的最優(yōu)。雖然還是在全局的框架下,但是整體的計算效率已相較于全局算法有了很大提升。
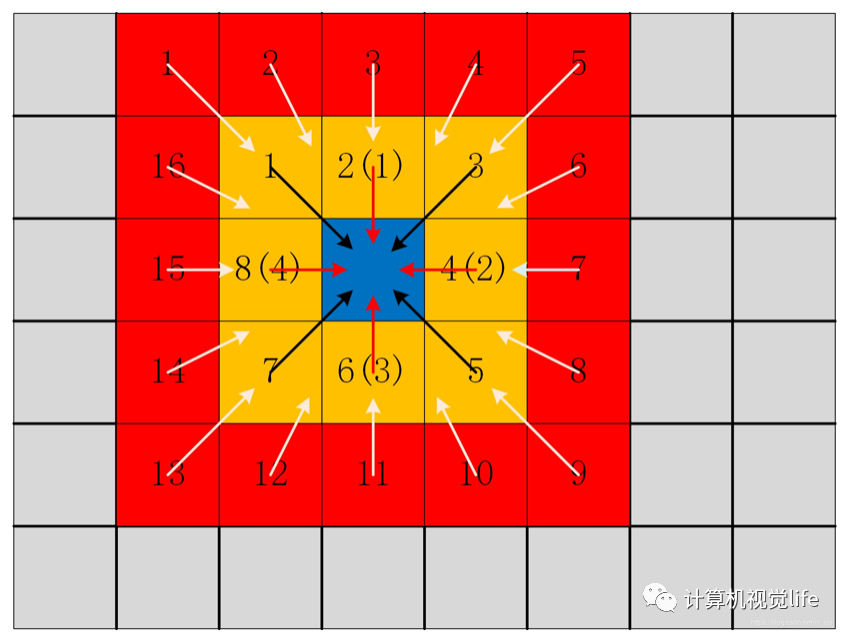
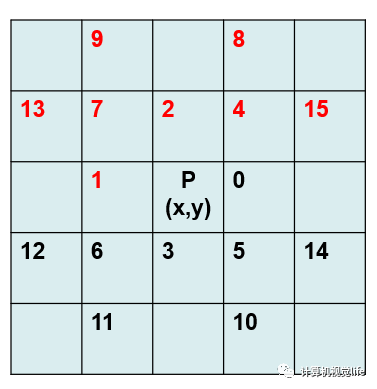
for (int row = 0; row < rows; ++row)
{
for (int col = 0; col < cols; ++col)
{
for (unsigned int path = 0; path < firstScanPaths.size(); ++path)
{
for (int d = 0; d < disparityRange; ++d)
{
S[row][col][d] += aggregateCost(row, col, d, firstScanPaths[path], rows, cols, disparityRange, C, A[path]);
}
}
}
lastProgressPrinted = printProgress(row, rows - 1, lastProgressPrinted);
}
aggregateCost(row, col, d, firstScanPaths[path], rows, cols, disparityRange, C, A[path])。輸入的參數(shù)中(row,col,d)相當于確定了視差空間中三維點的位置,firstScanPaths[path]則確定了是哪條路徑,或者可以更直觀的理解為是像素領(lǐng)域內(nèi)哪個相鄰像素,(rows,cols,disparityRange)則確定了視差空間的范圍,C為上一步代價計算得到的三維代價矩陣,最后的A[path]也是一個三維矩陣,用來存儲對應(yīng)方向的聚集代價,返回值則是A[row][col][d]。以下為該函數(shù)的實現(xiàn):unsigned short aggregateCost(int row, int col, int d, path &p, int rows, int cols, int disparityRange, unsigned short ***C, unsigned short ***A)
{
unsigned short aggregatedCost = 0;
aggregatedCost += C[row][col][d]; //像素匹配的 cost 值
// 1. 邊界條件,直接為C
if (row + p.rowDiff < 0 || row + p.rowDiff >= rows || col + p.colDiff < 0 || col + p.colDiff >= cols)
{
A[row][col][d] += aggregatedCost;
return A[row][col][d];
}
// 2. 若未超出邊界 ,則進行相應(yīng)方向的代價聚合
unsigned short minPrev, minPrevOther, prev, prevPlus, prevMinus;
prev = minPrev = minPrevOther = prevPlus = prevMinus = MAX_SHORT;
//設(shè)置初始代價為最大值
//minPrev: 對應(yīng)路徑的視差代價最小值
// 對于該路徑方向上,上一個像素,在其視差范圍內(nèi)進行循環(huán)
for (int disp = 0; disp < disparityRange; ++disp)
{
unsigned short tmp = A[row + p.rowDiff][col + p.colDiff][disp];
//找到這個路徑下,前一個像素取不同視差值時最小的A,即為最后減去的那一項,minPrev
if(minPrev > tmp){minPrev = tmp;}
//前一個像素視差取值為d時,即和當前像素的視差相等時,最小的A.
if(disp == d)
{ prev = tmp;}
//前一個像素視差取值為d+1時,即和當前像素的視差相差1時,最小的A,最后將加懲罰系數(shù)P1.
else if(disp == d + 1)
{ prevPlus = tmp;}
//前一個像素視差取值為d-1時,即和當前像素的視差相差1時,最小的A,最后將加懲罰系數(shù)P1.
else if (disp == d - 1)
{ prevMinus = tmp;}
//前一個像素視差與當前像素的視差相差大于等于2時,最小的A,最后將加懲罰系數(shù)P2.
else
{ minPrevOther = tmp;}
}
/* 計算四種情況下的代價最小值 */
aggregatedCost += std::min(std::min((int)prevPlus + SMALL_PENALTY, (int)prevMinus + SMALL_PENALTY), std::min((int)prev, (int)minPrevOther + LARGE_PENALTY));
aggregatedCost -= minPrev; //避免值過大,減小內(nèi)存
A[row][col][d] += aggregatedCost;
return A[row][col][d];
}
視差計算步驟其實非常簡單,通常直接利用贏家通吃(WTA)算法,即選擇某一個像素在所有視差值中最小的那一個即可,這也間接說明上一步,也即代價聚集步驟后所得到的視差空間中的代價值需要非常準確,那將直接決定算法的準確度。視差優(yōu)化則是對計算得到的視差圖進行進一步的優(yōu)化,包括剔除粗差,亞像素插值,平滑等等。比如經(jīng)常使用的左右一致性檢查,可用來剔除遮擋點所產(chǎn)生的錯誤匹配,對視差圖的改進比較大,有時候甚至可以成為許多算法的“遮羞布”。亞像素插值是對WTA得到的整像素進行精化,通常使用二次曲線擬合來獲得子像素的視差。平滑則是使用一些平滑算子對視差圖進行平滑處理。
本文簡要介紹了SGM的思想,并輔以部分代碼以助于理解。近年來深度學(xué)習(xí)大熱,SGM與深度學(xué)習(xí)的結(jié)合逐漸成為趨勢,網(wǎng)盤中所提供的文章與開源代碼可供讀者參考,若有錯漏,歡迎批評與不吝賜教。
交流群
歡迎加入公眾號讀者群一起和同行交流,目前有SLAM、三維視覺、傳感器、自動駕駛、計算攝影、檢測、分割、識別、醫(yī)學(xué)影像、GAN、算法競賽等微信群(以后會逐漸細分),請掃描下面微信號加群,備注:”昵稱+學(xué)校/公司+研究方向“,例如:”張三 + 上海交大 + 視覺SLAM“。請按照格式備注,否則不予通過。添加成功后會根據(jù)研究方向邀請進入相關(guān)微信群。請勿在群內(nèi)發(fā)送廣告,否則會請出群,謝謝理解~
