一份數(shù)學小白也能讀懂的「馬爾可夫鏈蒙特卡洛方法」入門指南
日期:2020年09月03日
正文共:4007字13圖
預(yù)計閱讀時間:11分鐘
來源:CSDN
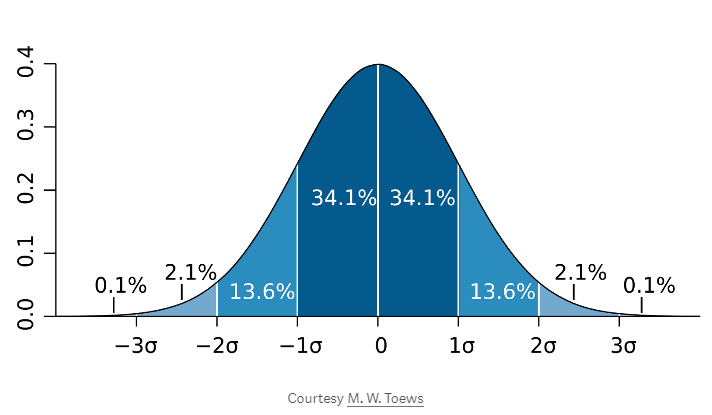 ?
?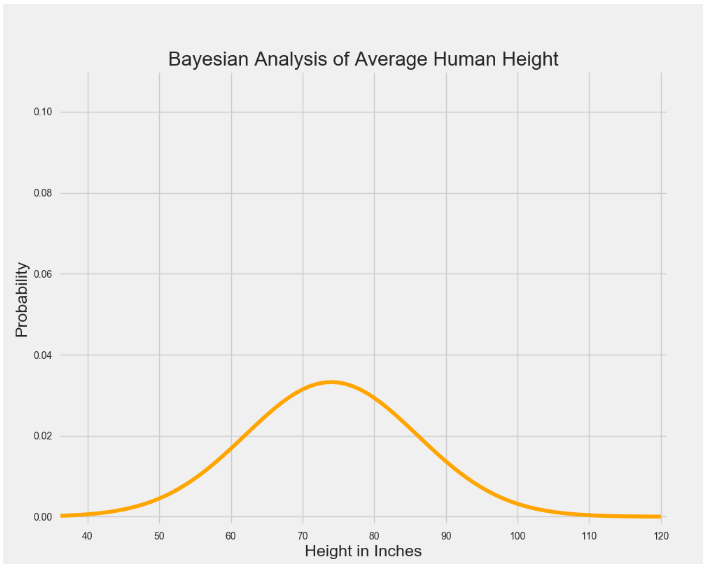 ?
?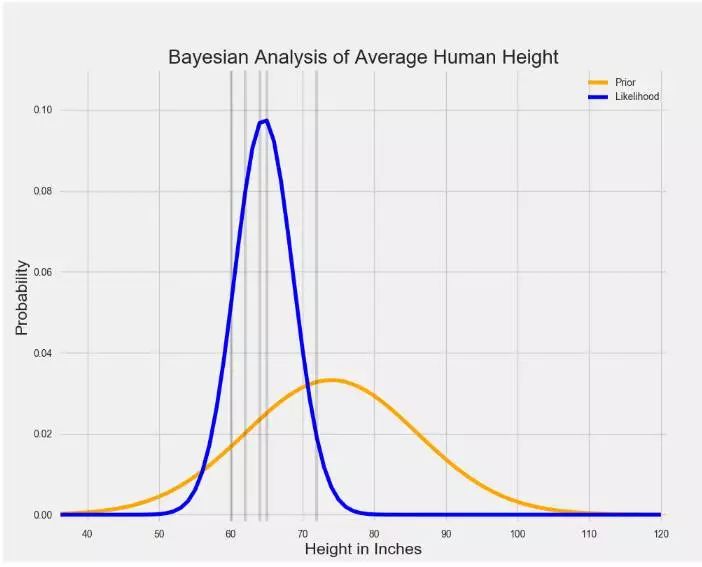 ?
?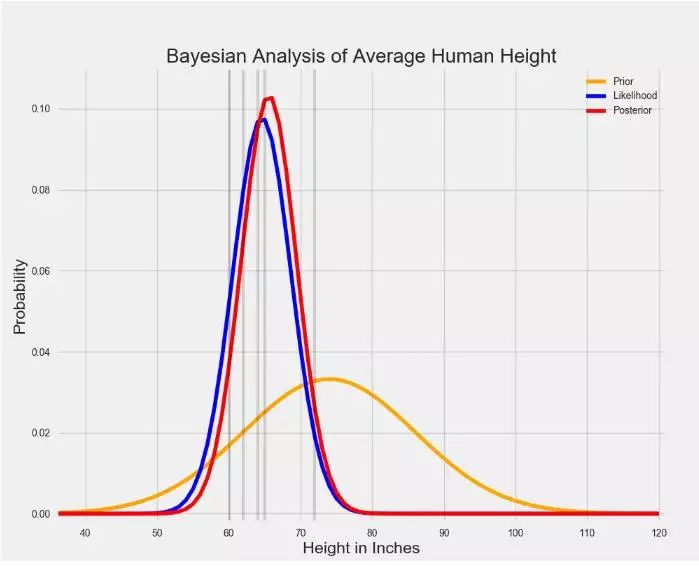 ?
? ?
? ??
?? ??
?? ?
?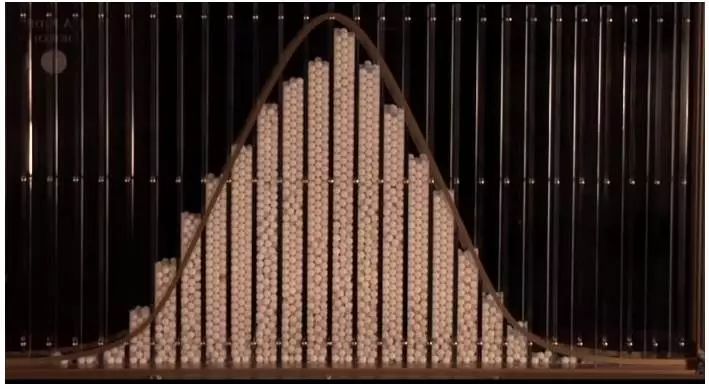 ?
?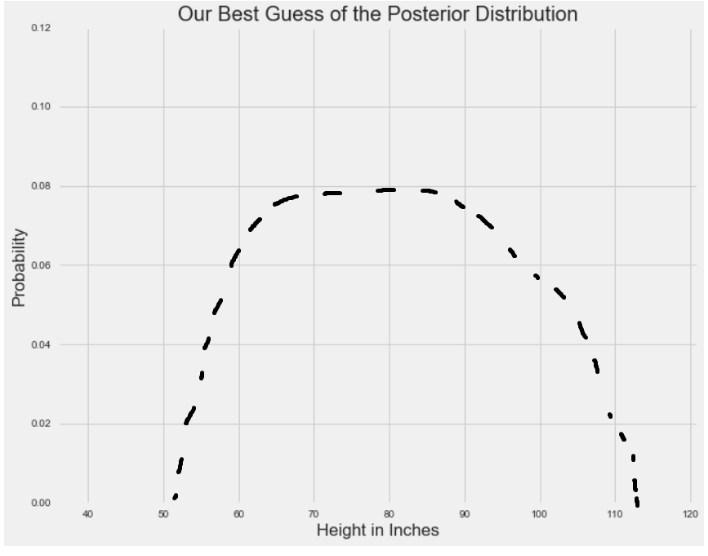 ?
?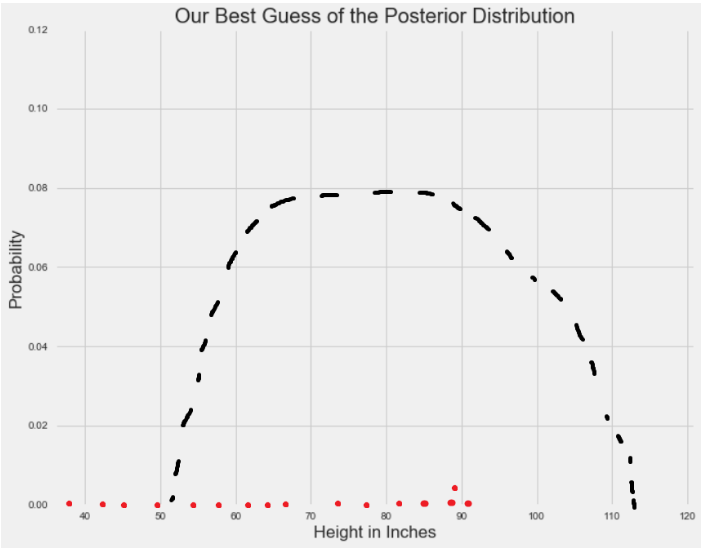 ?
?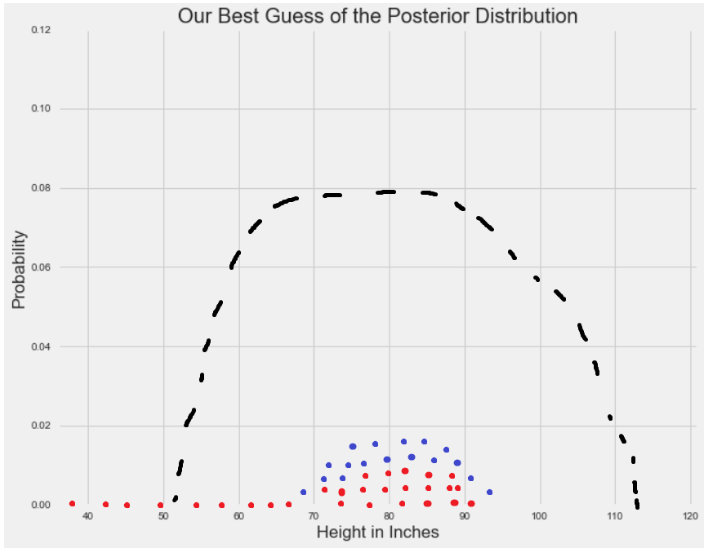 ?
? ?
?—?THE END —

評論
圖片
表情
<b id="afajh"><abbr id="afajh"></abbr></b>
 下載APP
下載APP日期:2020年09月03日
正文共:4007字13圖
預(yù)計閱讀時間:11分鐘
來源:CSDN
 ?
? ?
? ?
? ?
? ?
? ??
?? ??
?? ?
? ?
? ?
? ?
? ?
? ?
?—?THE END —

<b id="afajh"><abbr id="afajh"></abbr></b>