Go 數(shù)據(jù)結(jié)構(gòu)和算法篇(十二):字符串匹配之 KMP 算法

KMP 算法可以說是字符串匹配算法中最知名的算法了,KMP 算法是根據(jù)三位作者(D.E.Knuth,J.H.Morris 和 V.R.Pratt)的名字來命名的,算法的全稱是 Knuth Morris Pratt 算法,簡稱為 KMP 算法。
一、核心思想
假設(shè)主串是 a,模式串是 b。在模式串與主串匹配的過程中,當(dāng)遇到不可匹配的字符的時候,我們希望找到一些規(guī)律,可以將模式串往后多滑動幾位,跳過那些肯定不會匹配的情況,從而避免 BF 算法這種暴力匹配,提高算法性能。下面我們來探討下這個規(guī)律如何找到。
參考下面?zhèn)€主串和模式串的匹配,當(dāng)模式串移動到當(dāng)前位置,比對到最后一個字符 D 時,發(fā)現(xiàn)與主串不匹配,如果按照 BF 算法,就是把模式串往后移一位,再逐個比較,這樣做固然可以,但是效率很差:
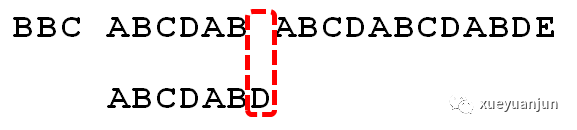
一個基本事實是,當(dāng) D 與主串不匹配時,我們已知前面的主串序列是 ABCDA,如果把模式串往后移一位肯定和主串不匹配,我們可不可以直接把模式串移到下一個可能和 A 匹配的主串位置?
實際上,KMP 算法正是基于這一理念,設(shè)法利用這個已知信息,不把模式串移到已經(jīng)比較過的位置,繼續(xù)把它向后移,這樣綜合下來就極大提高了搜索匹配效率。
怎么找到這個規(guī)律,確定把模式串往后移多少位呢?在模式串和主串匹配的過程中,我們把不能匹配的那個字符仍然叫作「壞字符」,把已經(jīng)匹配的那段字符串叫作「好前綴」:
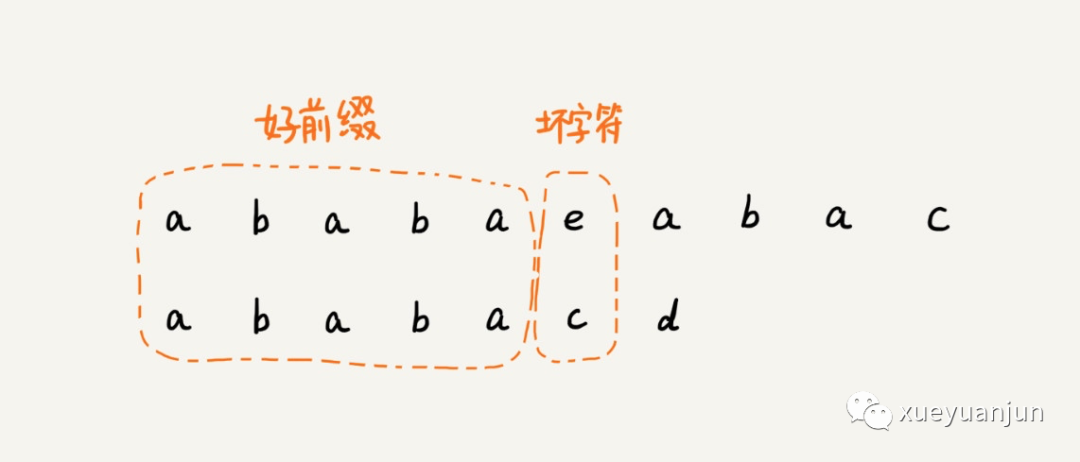
在模式串和主串匹配的過程中,當(dāng)遇到壞字符后,對于已經(jīng)比對過的好前綴,我們只需要拿好前綴本身,在它的后綴子串中,查找最長的那個可以跟好前綴的前綴子串匹配的下標(biāo)位置,然后將模式串后移到該位置即可。
這里,我們要解釋幾個概念:
后綴子串:以某個字符串最后一個字符為尾字符的子串(不包含字符串自身),比如上面的
ababa,后綴子串為baba、aba、ba、a;前綴子串:以某個字符串第一個字符為首字符的子串(不包含字符串自身),還是以
ababa為例,前綴子串為a、aba、abab;最長可匹配后綴子串:后綴子串與前綴子串最長可匹配子串,也可叫做共有子串,以
ababa為例,自然是aba了,長度為 3;最長可匹配前綴子串:與上面定義相對,即前綴子串與后綴子串最長可匹配子串。最長可匹配前綴子串和最長可匹配后綴子串肯定是一樣的。
假設(shè)壞字符所在位置是 j,最長可匹配后綴子串長度為 k,則模式串需要后移的位數(shù)為 j-k。每當(dāng)我們遇到壞字符,就將模式串后移 j-k 位,直到模式串與對應(yīng)主串字符完全匹配;如果移到最后還是不匹配,則返回 -1。這就是 KMP 算法的核心思想。
二、實現(xiàn)原理
了解了核心思想,接下來,就可以考慮如何實現(xiàn) KMP 算法了,實現(xiàn) KMP 算法最核心的部分是構(gòu)建一個用來存儲模式串中每個前綴子串(這些前綴都有可能是好前綴)最長可匹配前綴子串的結(jié)尾字符下標(biāo)數(shù)組,我們把這個數(shù)組叫做 next 數(shù)組,對于上面 ababacd 這個模式串而言,對應(yīng)的 next 數(shù)組如下:
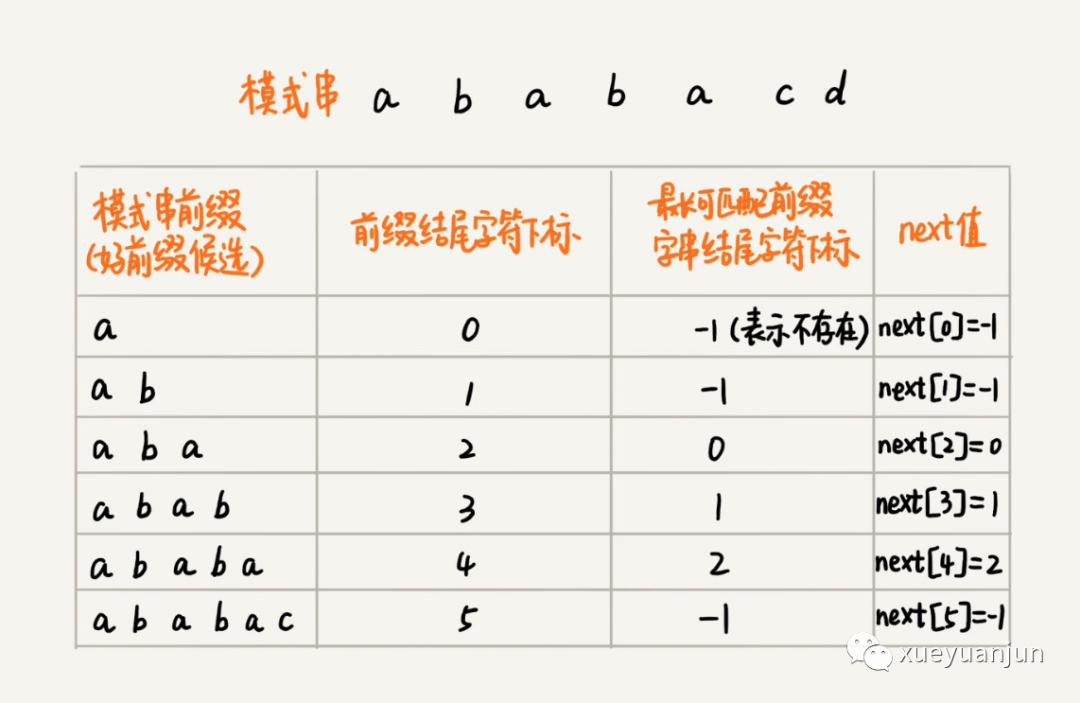
其中,數(shù)組的下標(biāo)是前綴子串結(jié)尾字符下標(biāo),數(shù)組的值是這個前綴的最長可匹配前綴子串的結(jié)尾字符下標(biāo)。
有了這個 next 數(shù)組,我們就可以實現(xiàn) KMP 匹配算法的核心代碼了。
三、示例代碼
下面是一個基于 KMP 算法實現(xiàn)的 Golang 版字符串查找函數(shù):
package main
import "fmt"
// 生成 next 數(shù)組
func generateNext(p string) []int {
m := len(p)
next := make([]int, m, m)
next[0] = -1
next[1] = 0
i, j := 0, 1 // 前綴子串、后綴子串起始位置
// 因為是通過最長可匹配前綴子串計算,所以 j 的值最大不會超過 m-1
for j < m - 1 {
if i == -1 || p[i] == p[j] {
i++
j++
// 設(shè)置當(dāng)前最長可匹配前綴子串結(jié)尾字符下標(biāo)
next[j] = i
} else {
// 如果 p[i] != p[j],回到上一個最長可匹配前綴子串結(jié)尾字符下標(biāo)
i = next[i]
}
}
return next
}
// KMP 算法實現(xiàn)函數(shù)
func kmpSearch(s, p string) int {
n := len(s) // 主串長度
m := len(p) // 模式串長度
next := generateNext(p) // 生成 next 數(shù)組
i, j := 0, 0
for i < n && j < m {
// 如果主串字符和模式串字符不相等,
// 更新模式串壞字符下標(biāo)位置為好前綴最長可匹配前綴子串尾字符下標(biāo)
// 然后從這個位置重新開始與主串匹配
// 相當(dāng)于前面提到的把模式串向后移動 j - k 位
if j == -1 || s[i] == p[j] {
i++
j++
} else {
j = next[j]
}
}
if j == m {
// 完全匹配,返回下標(biāo)位置
return i - j
} else {
return -1
}
}
// 基于 KMP 算法實現(xiàn)查找字符串子串函數(shù)
func strStrV2(haystack, needle string) int {
// 子串長度=0
if len(needle) == 0 {
return 0
}
//主串長度=0,或者主串長度小于子串長度
if len(haystack) == 0 || len(haystack) < len(needle) {
return -1
}
// 子串長度=1時單獨(dú)判斷
if len(needle) == 1 {
i := 0
for ; i < len(haystack); i++ {
if haystack[i] == needle[0] {
return i
}
}
return -1
}
// 其他情況走 KMP 算法
return kmpSearch(haystack, needle)
}
func main() {
s := "Hello, 學(xué)院君!"
p := "學(xué)院君"
pos := strStrV2(s, p)
fmt.Printf("Find \"%s\" at %d in \"%s\"\n", p, pos, s)
}
運(yùn)行上述代碼,打印結(jié)果如下,說明字符串查找函數(shù)可以正常工作:

四、性能分析
KMP 算法比 BF 算法實現(xiàn)起來要復(fù)雜的多,不過帶來的好處是執(zhí)行效率的提升,綜合 KMP 算法實現(xiàn)函數(shù)和 next 數(shù)組生成函數(shù),它的時間復(fù)雜度是 O(n+m),其中 n 是主串長度,m 是子串長度,m 和 n 的值越大,性能比 BF 算法更好,考慮到對于較長的主串,m 相對于 n 而言一般可以忽略,所以可以把 KMP 算法的時間復(fù)雜度近似看作 O(n)。
這個性能還是相當(dāng)不錯的,因此,KMP 算法被廣泛用于字符串查找和匹配場景。
(本文完)
推薦閱讀
