算法數(shù)據(jù)結構 | 只要30行代碼，實現(xiàn)快速匹配字符串的KMP算法

今天是算法數(shù)據(jù)結構專題的第29篇文章，我們來聊一個新的字符串匹配算法——KMP。

KMP這個名字不是視頻播放器，更不是看毛片，它其實是由Knuth、Morris、Pratt這三個大牛名字的合稱。老外很喜歡用人名來命名算法或者是定理，數(shù)學里就有一堆，什么高斯定理、歐拉函數(shù)什么的。但是中國人更傾向于從表意上來給一個概念命名，比如勾股定理、同余定理等等。之前覺得用人名命名很洋氣，作者可以青史留名，后來想想這也是英文表意能力不足，很難用表意的方式起名的體現(xiàn)。

扯遠了，我們回到正題。

應用場景

在計算機領域當中字符串匹配其實是一個非常常見的問題，我們使用它的場景也多到不可計數(shù)。比如在一個已經(jīng)打開的頁面當中搜索關鍵詞，再比如說git里面的代碼變動的記錄，以及論文的查重等等。在這些問題當中有些情況可能還好，比如說我們搜索一個關鍵詞，因為關鍵詞并不長，我們暴力枚舉也不會特別耗時。但是在有些問題當中明顯暴力匹配是無法勝任的，比如論文查重。一篇論文動輒上千詞，要和庫中的上萬篇文章進行查重掃描，這當中的工作量可想而知。如果是暴力枚舉算法那查重顯然會查到天荒地老。

所以早期的時候字符串匹配是一個難題，既然是難題那么顯然就會有很多人來研究，也因此出了很多成果，很多大牛發(fā)表了字符串匹配的算法，其中KMP算法由于效率很高、實現(xiàn)復雜度低被應用得最廣。到這里，我們就知道KMP算法是用來字符串匹配的。

比方說我們有兩個字符串，A串是：I hate learning English. B串是hate learning，很明顯B串是A串的字符串。如果我們暴力枚舉來判斷的話，我們需要遍歷A串當中的每一個起始位置是否能夠完成匹配，那么復雜度顯然是。通過KMP算法，我們可以在的時間內做到這點。

著名的大佬matrix67在KMP算法的介紹博客當中有一句著名的騷話，當你有一個喜歡的MM，你可以委婉地問她：“假如你要向你喜歡的人表白的話，我的名字是你的告白語中的子串嗎？”

Next數(shù)組

KMP算法的核心精髓只有一個就是Next數(shù)組，但是這個概念并不太容易理解，很多人學KMP放棄就是折戟在了Next這個數(shù)組上。

我們先把Next數(shù)組是怎么來的放在一邊，先來看下Next數(shù)組是用來干嘛的，它起作用的原理是什么，最后再來討論Next數(shù)組怎么來的問題。根據(jù)我的理解，Next數(shù)組其實就是一個中途開始的機會，也就是當我們在枚舉匹配的時候，發(fā)現(xiàn)了不匹配的情況，我們不是從頭開始，而是從一個最大可能的中間結果開始。

我們來看個例子：

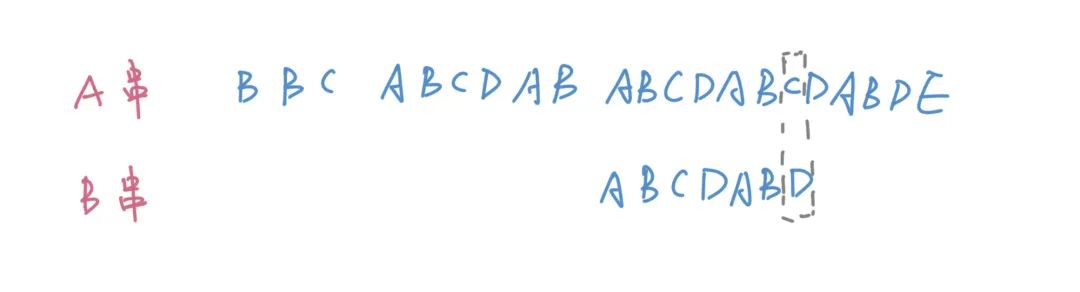
上圖中上面的是A串，下面的是B串，我們在匹配的過程當中發(fā)現(xiàn)B串的前面幾位都匹配上了，而在最后一位匹配失敗。按照常規(guī)的做法，我們應該是移動到下一個位置從頭開始匹配。但是這是非常浪費的，因為我們觀察下可以發(fā)現(xiàn)失敗位置的ABC和B串開頭的ABC是可以構成匹配的。

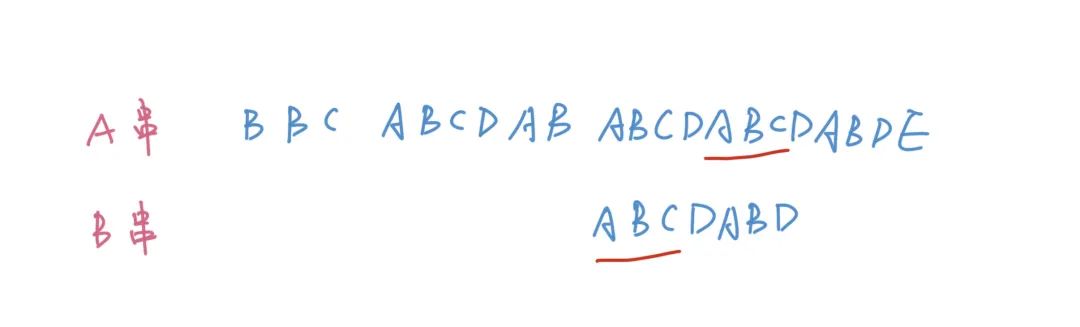
我們之前失敗的時候判斷的是以C結尾的ABCDABC和B串的匹配，在這一次匹配失敗之后，我們可以繼續(xù)嘗試匹配其他以C結尾的前綴串，比如ABC。這樣我們就可以從中間狀態(tài)開始，而節(jié)省了許多次不必要的枚舉。但問題就來了，這個中間結果是怎么來的呢，我們怎么知道當下失敗了上一個可行的中間結果是哪一個？

對，沒有錯，前面說到的Next數(shù)組就是用來存儲中間結果的。所以Next可以理解成下一次機會的意思，這樣就好理解了。由于我們是在A串當中尋找B串，所以這個Next數(shù)組應該是針對B的，記錄B中每一個位置如果匹配失敗，它的前面一個可行的中間狀態(tài)是哪一個。

我們先寫出來B的Next數(shù)組，等會再去研究它是怎么得到的。為了簡化編碼，我們假設字符串是從1位置開始的，所以我們在0的位置添加一個$符號作為占位符。對于大部分情況都是沒有重來的機會的，失敗了直接歸零。而其中的A和B兩個位置是有重來機會的，因為B的前綴當中出現(xiàn)了A和AB。所以如果在匹配ABD的時候失敗了，我們還可以從AB處再次開始嘗試匹配ABC。

算法原理

我們想象一根指針指向了B數(shù)組當中接下來要匹配的位置，如果匹配失敗了，它就會跳轉到Next數(shù)組當中記錄的位置去，匹配成功了我們就向后移動一位。在有了Next數(shù)組之后，我們寫出代碼來真的很容易了：

def?kmp(var_str,?template_str):
????#?var_str即A串
????#?template_str模式串即B串
????#?我們在兩個字符串前加上了占位符
????var_str?=?'$'?+?var_str
????template_str?=?'$'?+?template_str
????next?=?generate_next(template_str)
????n,?m?=?len(var_str),?len(template_str)
????#?head指向要匹配的位置的前一位
????head?=?0
????for?i?in?range(1,?n):
????????#?由于next數(shù)組很長，可能失敗多次
????????#?直到head+1的位置能匹配上或者head等于0
????????while?head?>?0?and?template_str[head+1]?!=?var_str[i]:
????????????head?=?next[head]
????????
????????#?匹配上了則head變長一位
????????if?template_str[head+1]?==?var_str[i]:
????????????head?+=?1
????????
????????#?如果head長度等于B串了，則表示匹配成功
????????if?head?==?m?-?1:
????????????return?True
????
????return?False

對于A串中的每一個位置來說，我們都在B串當中遍歷了每一個有可能構成匹配的前綴。所以說這個算法是可行的，一定可以獲得解。另外一個問題是復雜度的問題，為什么我們用了兩重循環(huán)，但仍然是的算法呢？

其實很簡單，因為while循環(huán)只會讓head減小，而不會讓head增加。head增加是在for循環(huán)里執(zhí)行的，也就是說head最多增加n次。那么對應的while循環(huán)也就最多執(zhí)行n次，因為head是非負的。所以while循環(huán)在整個for循環(huán)執(zhí)行的過程當中最多執(zhí)行了n次，整體執(zhí)行的次數(shù)仍然是級別的而不是級，當然是線性的算法。

求解Next

到這里，問題只剩下了一個，就是這個Next怎么來呢？

其實我們在之前講Next數(shù)組的使用的時候已經(jīng)泄露天機了，我們再來看下上圖，不知道大家能感覺到什么。

后面一個A的Next值是1，也就是第一個A的下標，后面一個B的Next值是2，也就是第一個B的下標。換句話說第二個A能夠和位置1的A匹配，后面的AB能和前綴的AB匹配。也就是說Next數(shù)組其實就是B數(shù)組自己和自己匹配的結果，我們在一開始的時候將整個Next數(shù)組全部置為0，然后依次遞推迭代出所有的Next的值。

我們在求解Next[i]的時候我們可以利用上Next[i-1]的值，因為Next[i-1]存儲的是能夠與B[i-1]匹配的前綴的結尾位置。如果B[Next[i-1]+1]等于B[i]，那么說明Next[i] = Next[i-1] + 1。如果不等的話，我們可以用while循環(huán)來尋找能夠匹配上的前綴。也就是說這是一個遞推的過程，不過要注意一點我們計算Next數(shù)組要從2開始，因為對于1來說，Next[1]一定等于0。

def?generate_next(var_str):
????n?=?len(var_str)
????next?=?[0?for?_?in?range(n)]
????for?i?in?range(2,?n):
????????#?用next[i-1]作為開始尋找能夠匹配上的最長next[i]
????????head?=?next[i-1]
????????while?head?>?0?and?var_str[head+1]?!=?var_str[i]:
????????????head?=?next[head]
??
????????#?如果匹配上了，head+1
????????if?var_str[head+1]?==?var_str[i]:
????????????head?=?head?+?1
????????#?記錄下來
????????next[i]?=?head
????return?next

總結

到這里，我們關于KMP算法的介紹就結束了，不知道大家看完之后感受如何，是不是有點蒙圈呢？

其實蒙圈是正常的，我第一次學的時候足足看了好幾遍才算是看明白。這畢竟是一個比較巧妙的算法，想要通過閱讀一篇文章就完全學會還是比較困難的，最好的還是親自動手實現(xiàn)一下試試。KMP算法我最大的感受就是如果你把整個算法的邏輯都串起來了，那么即使自己從頭到尾推導一遍難度也不是很大（我就在面試當中推導過一次）。如果你沒能把邏輯串起來，那么覺得難理解看不懂是正常的，你可能需要再讀一遍或者是尋找一些其他的資料查漏補缺。