KMP算法(字符串匹配)

字符串匹配是常見的算法題,就有一個(gè)字符串判斷里面是否包含另一個(gè)字符串。
舉例來說,有一個(gè)字符串"AAAAAABC"(主串),我想知道,里面是否包含另一個(gè)字符串"AAAB"(模式串)?對主串和模式串做匹配。
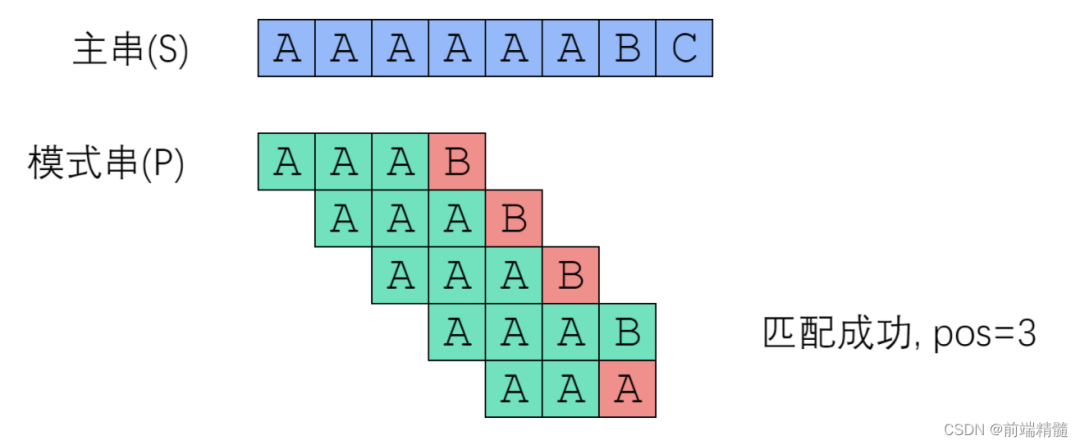
首先,字符串 "AAAAAABC" 的第一個(gè)字符與搜索詞 "AAAB" 的第一個(gè)字符,進(jìn)行比較。
AAAAAABCAAAB
字符串有一個(gè)字符與搜索詞的第一個(gè)字符相同,接著比較字符串和搜索詞的下一個(gè)字符,還是相同。直到字符串有一個(gè)字符,與搜索詞對應(yīng)的字符不相同為止。
當(dāng)字符串的索引為 3 的時(shí)候發(fā)現(xiàn)不相等,這時(shí),最自然的反應(yīng)是,將搜索詞整體后移一位,再從頭逐個(gè)比較。
AAAAAABCAAAB
基于這個(gè)想法我們可以得到以下的程序:
function bf(ts, ps) {let t = ts;let p = ps;let i = 0; // 主串的位置let j = 0; // 模式串的位置while (i < t.length && j < p.length) {if (t[i] === p[j]) { // 當(dāng)兩個(gè)字符串相同,就比較下一個(gè)i++;j++;} else {i = i - j + 1; // 一旦不匹配,i后退j = 0; // j歸0}}if (j === p.length) {return i - j} else {return -1;}}console.log(bf('AAAAAABC', 'AAAB'))
上面的程序是沒有問題的,但不夠好!這是暴力解法復(fù)雜度 O(nm) 的。這太慢了!
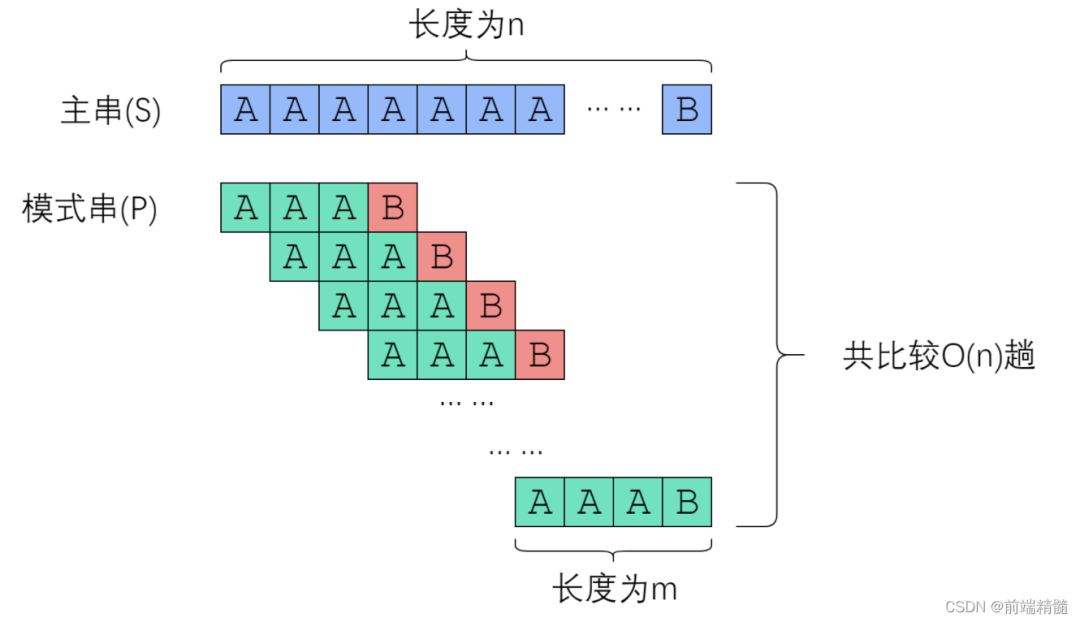
我們很難降低字符串比較的復(fù)雜度(因?yàn)楸容^兩個(gè)字符串,真的只能逐個(gè)比較字符)。因此,我們考慮降低比較的趟數(shù)。
跳過不可能成功的字符串比較
有些趟字符串比較是有可能會(huì)成功的;有些則毫無可能。而如果我們跳過那些絕不可能成功的字符串比較,則可以希望復(fù)雜度降低到能接受的范圍。
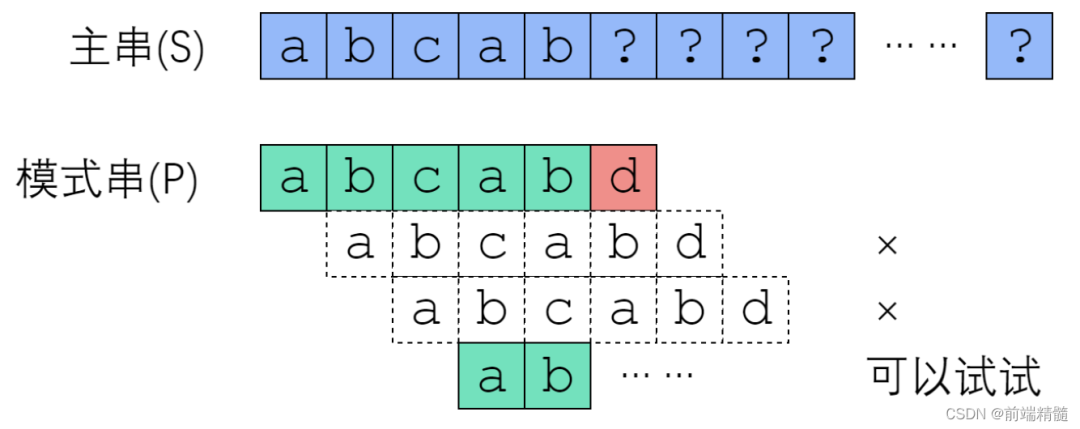
一個(gè)基本事實(shí)是,當(dāng) d 不匹配時(shí),你其實(shí)知道前面五個(gè)字符是"abcab"。如果是人為來尋找的話,肯定不會(huì)再把 i 移動(dòng)到索引為1,我們會(huì)直接移動(dòng)到索引為3!就可以來到第二個(gè)"ab"的位置。
所以,整個(gè)KMP的重點(diǎn)就在于當(dāng)某一個(gè)字符與主串不匹配時(shí),我們應(yīng)該知道指針要移動(dòng)到哪?
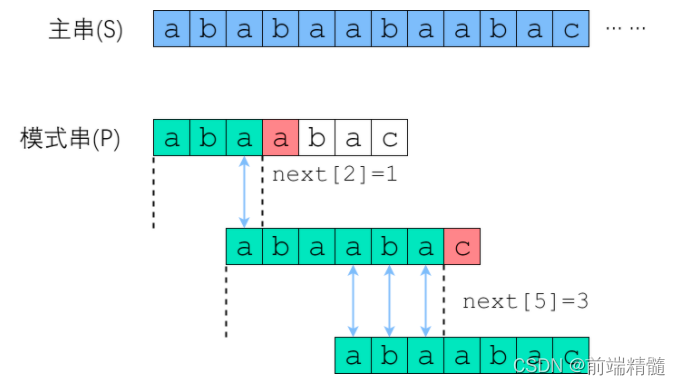
移動(dòng)位數(shù) = 已匹配的字符數(shù) - 對應(yīng)的部分匹配值首先,要了解兩個(gè)概念:"前綴"和"后綴"。"前綴"指除了最后一個(gè)字符以外,一個(gè)字符串的全部頭部組合;"后綴"指除了第一個(gè)字符以外,一個(gè)字符串的全部尾部組合。
"abcab"的前綴為[a, ab, abc, abca],后綴為[bcab, cab, ab, b],共有元素為"ab",長度為2;
"部分匹配"的實(shí)質(zhì)是,有時(shí)候,字符串頭部和尾部會(huì)有重復(fù)。比如,"abcab"之中有兩個(gè)"ab",那么它的"部分匹配值"就是2("ab"的長度)。搜索詞移動(dòng)的時(shí)候,第一個(gè)"ab"向后移動(dòng)到索引為3(字符串長度5-部分匹配值2),就可以來到第二個(gè)"ab"的位置。
根據(jù)nxt數(shù)組加快字符串匹配。
function getNext(p) {let nxt = [];nxt.push(0); // next[0] 必然是0let x = 1; // 因此 nxt[1] 開始求let now = 0;while (x < p.length) {if (p[now] === p[x]) { // 如果 p[now] == p[x] ,則可以向右擴(kuò)展一位now += 1x += 1nxt.push(now)} else if (now) {now = nxt[now - 1] // 縮小 now,改成 nxt[now - 1]} else {nxt.push(0) // now 已經(jīng)為0,無法再縮小了, 故 nxt[x] = 0x += 1}}return nxt}console.log(getNext('abcab'))// [ 0, 0, 0, 1, 2 ]
根據(jù)nxt數(shù)組移動(dòng)標(biāo)尺。
function bf(ts, ps)let t = ts;let p = ps;let i = 0; // 主串的位置let j = 0; // 模式串的位置let nxt = getNext(ps)while (i < t.length && j < p.length) {if (t[i] === p[j]) { // 當(dāng)兩個(gè)字符串相同,就比較下一個(gè)i++;j++;} else {// 失配了if (j) {j = nxt[j - 1] // 根據(jù)nxt數(shù)組移動(dòng)標(biāo)尺} else {i++; // ps[0]失配了,直接把標(biāo)尺往右移動(dòng)一位}}}if (j === p.length) {return i - j} else {return -1;}}