機(jī)器學(xué)習(xí)三人行(系列十)----機(jī)器學(xué)習(xí)降壓神器(附代碼)

系列九我們從算法組合的角度一起實(shí)戰(zhàn)學(xué)習(xí)了一下組合算法方面的知識(shí),詳情戳下鏈接:
機(jī)器學(xué)習(xí)三人行(系列九)----千變?nèi)f化的組合算法(附代碼)
但是,我們也知道算法組合會(huì)造成整體算法時(shí)間成本的增加,所以今天我們從降維的角度來(lái)看下,如何給算法降低時(shí)間成本。
在這一期中,我們將主要討論一下幾方面內(nèi)容:
維度災(zāi)難
降維的主要途徑
PCA(主成分分析)
Kernel PCA
LLE(局部線性嵌入)
文末附相關(guān)代碼關(guān)鍵字,可在公眾號(hào)中回復(fù)關(guān)鍵字下載查看。
一. 維度災(zāi)難
許多機(jī)器學(xué)習(xí)問(wèn)題涉及特征多達(dá)數(shù)千乃至數(shù)百萬(wàn)個(gè)。正如我們將看到的,這不僅讓訓(xùn)練變得非常緩慢,而且還會(huì)使得找到一個(gè)好的解決方案變得更加困難。這個(gè)問(wèn)題通常被稱為維度災(zāi)難。
幸運(yùn)的是,在現(xiàn)實(shí)世界的問(wèn)題中,通常可能會(huì)減少特征的數(shù)量,從而將棘手的問(wèn)題變成易于處理的問(wèn)題。例如,考慮MNIST圖像(在系列四中介紹):圖像邊界上的像素幾乎總是白色的,所以你可以從訓(xùn)練集中完全丟棄這些像素而不會(huì)丟失太多信息。?而且,兩個(gè)相鄰像素通常是高度相關(guān)的:如果將它們合并成一個(gè)像素(例如,通過(guò)取兩個(gè)像素強(qiáng)度的平均值),則不會(huì)丟失太多信息。
除了加速訓(xùn)練之外,降維對(duì)于數(shù)據(jù)可視化(或DataViz)也非常有用。將維度數(shù)量減少到兩個(gè)(或三個(gè))使得可以在圖表上繪制高維訓(xùn)練集,并且通常通過(guò)視覺上檢測(cè)諸如集群的圖案來(lái)獲得一些重要的見解。
我們習(xí)慣于三維生活,當(dāng)我們?cè)噲D想象一個(gè)高維空間時(shí),我們的直覺失敗了。即使是一個(gè)基本的4D超立方體,在我們的腦海中也難以想象,如下圖,更不用說(shuō)在1000維空間彎曲的200維橢球。
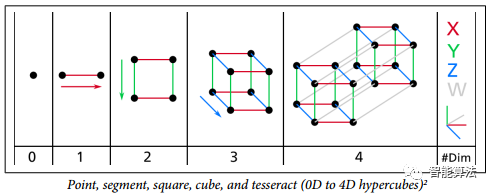
事實(shí)證明,許多事物在高維空間中表現(xiàn)得非常不同。例如,如果你選擇一個(gè)單位平方(1×1平方)的隨機(jī)點(diǎn),它將只有大約0.4%的機(jī)會(huì)位于小于0.001的邊界(換句話說(shuō),隨機(jī)點(diǎn)將沿任何維度“極端”這是非常不可能的)。但是在一個(gè)10000維單位超立方體(1×1×1立方體,有1萬(wàn)個(gè)1)中,這個(gè)概率大于99.999999%。高維超立方體中的大部分點(diǎn)都非常靠近邊界。
這更難區(qū)分:如果你在一個(gè)單位平方中隨機(jī)抽取兩個(gè)點(diǎn),這兩個(gè)點(diǎn)之間的距離平均約為0.52。如果在單位三維立方體中選取兩個(gè)隨機(jī)點(diǎn),則平均距離將大致為0.66。但是在一個(gè)100萬(wàn)維的超立方體中隨機(jī)抽取兩點(diǎn)呢?那么平均距離將是大約408.25(大約1,000,000 / 6)!
這非常違反直覺:當(dāng)兩個(gè)點(diǎn)位于相同的單位超立方體內(nèi)時(shí),兩點(diǎn)如何分離?這個(gè)事實(shí)意味著高維數(shù)據(jù)集有可能非常稀疏:大多數(shù)訓(xùn)練實(shí)例可能彼此遠(yuǎn)離。當(dāng)然,這也意味著一個(gè)新實(shí)例可能離任何訓(xùn)練實(shí)例都很遠(yuǎn),這使得預(yù)測(cè)的可信度表現(xiàn)得比在低維度數(shù)據(jù)中要來(lái)的差。簡(jiǎn)而言之,訓(xùn)練集的維度越多,過(guò)度擬合的風(fēng)險(xiǎn)就越大。
理論上講,維度災(zāi)難的一個(gè)解決方案可能是增加訓(xùn)練集的大小以達(dá)到足夠密度的訓(xùn)練實(shí)例。不幸的是,在實(shí)踐中,達(dá)到給定密度所需的訓(xùn)練實(shí)例的數(shù)量隨著維度的數(shù)量呈指數(shù)增長(zhǎng)。如果只有100個(gè)特征(比MNIST問(wèn)題少得多),那么為了使訓(xùn)練實(shí)例的平均值在0.1以內(nèi),需要比可觀察宇宙中的原子更多的訓(xùn)練實(shí)例,假設(shè)它們?cè)谒芯S度上均勻分布。
二. 降維的主要途徑
在深入研究具體的降維算法之前,我們來(lái)看看降維的兩種主要途徑:投影和流形學(xué)習(xí)。
2.1 投影
在大多數(shù)現(xiàn)實(shí)世界的問(wèn)題中,訓(xùn)練實(shí)例并不是在所有維度上均勻分布。許多特征幾乎是常量,而其他特征則高度相關(guān)(如前面討論MNIST)。結(jié)果,所有訓(xùn)練實(shí)例實(shí)際上位于(或接近)高維空間的低維子空間內(nèi)。這聽起來(lái)很抽象,所以我們來(lái)看一個(gè)例子。在下圖中,我們可以看到由圓圈表示的三維數(shù)據(jù)集。
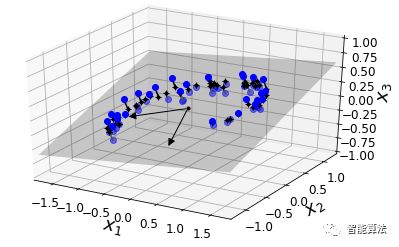
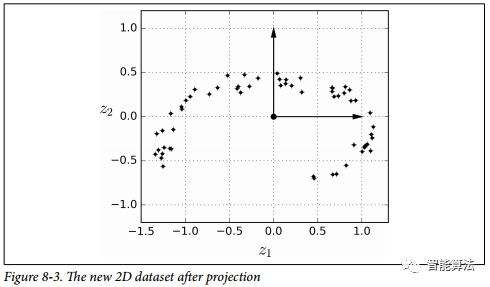
請(qǐng)注意,所有訓(xùn)練實(shí)例都靠近一個(gè)平面:這是高維(3D)空間的較低維(2D)子空間。現(xiàn)在,如果我們將每個(gè)訓(xùn)練實(shí)例垂直投影到這個(gè)子空間上(如連接實(shí)例到平面的短線所表示的那樣),我們就得到如下圖所示的新的2D數(shù)據(jù)集。當(dāng)當(dāng)!我們剛剛將數(shù)據(jù)集的維度從3D減少到了2D。請(qǐng)注意,軸對(duì)應(yīng)于新的特征z1和z2(平面上投影的坐標(biāo))。
然而,投影并不總是降維的最佳方法。在許多情況下,子空間可能會(huì)扭曲和轉(zhuǎn)動(dòng),如下圖所示的著名的瑞士滾動(dòng)玩具數(shù)據(jù)集。
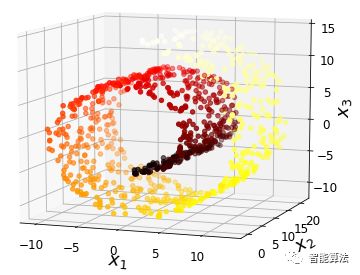
簡(jiǎn)單地投射到一個(gè)平面上(例如,通過(guò)丟棄特征x3)將會(huì)把瑞士卷的不同層擠壓在一起,如下圖的左邊所示。但是,您真正需要的是展開瑞士卷,以獲得下圖右側(cè)的2D數(shù)據(jù)集。
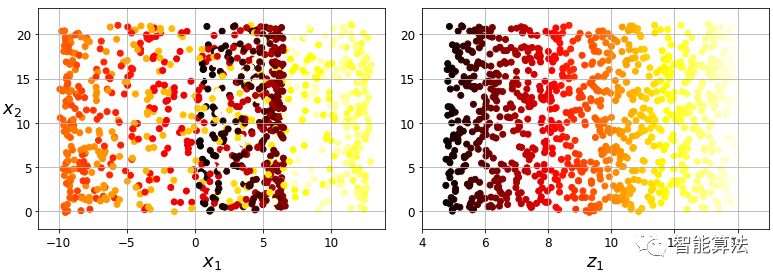
2.2 流形學(xué)習(xí)
瑞士卷是二維流形的一個(gè)例子。簡(jiǎn)而言之,二維流形是一種二維形狀,可以在更高維空間中彎曲和扭曲。更一般地,d維流形是局部類似于d維超平面的n維空間(其中d
許多降維算法通過(guò)對(duì)訓(xùn)練實(shí)例所在的流形進(jìn)行建模來(lái)工作; 這叫做流形學(xué)習(xí)。它依賴于流形假設(shè),也被稱為流形假設(shè),它認(rèn)為大多數(shù)現(xiàn)實(shí)世界的高維數(shù)據(jù)集靠近一個(gè)低得多的低維流形。這種假設(shè)通常是經(jīng)驗(yàn)性觀察到的。
再次考慮MNIST數(shù)據(jù)集:所有的手寫數(shù)字圖像都有一些相似之處。它們由連線組成,邊界是白色的,或多或少居中,等等。如果你隨機(jī)生成圖像,只有一小部分看起來(lái)像手寫數(shù)字。換句話說(shuō),如果您嘗試創(chuàng)建數(shù)字圖像,可用的自由度遠(yuǎn)遠(yuǎn)低于您可以生成任何想要的圖像的自由度。這些約束傾向于將數(shù)據(jù)集壓縮到較低的維度。
流形假設(shè)通常伴隨另一個(gè)隱含的假設(shè):如果在流形的較低維空間中表示,手頭的任務(wù)(例如分類或回歸)將更簡(jiǎn)單。例如,在下圖的第一行中,瑞士卷被分成兩類:在三維空間(在左邊),決策邊界相當(dāng)復(fù)雜,但是在2D展開的流形空間(在右邊 ),決策邊界是一條簡(jiǎn)單的直線。
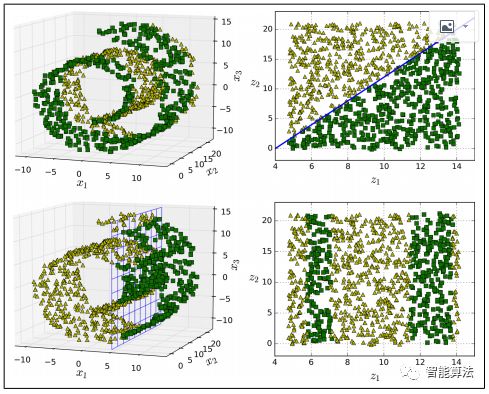
但是,這個(gè)假設(shè)并不總是成立。例如,在上圖右側(cè),判定邊界位于x1 = 5。這個(gè)判定邊界在原始三維空間(一個(gè)垂直平面)看起來(lái)非常簡(jiǎn)單,但是在展開的流形中它看起來(lái)更復(fù)雜 四個(gè)獨(dú)立的線段的集合)。
簡(jiǎn)而言之,如果在訓(xùn)練模型之前降低訓(xùn)練集的維數(shù),那么肯定會(huì)加快訓(xùn)練速度,但并不總是會(huì)導(dǎo)致更好或更簡(jiǎn)單的解決方案。這一切都取決于數(shù)據(jù)集。
到這里我們基本能夠很好地理解維度災(zāi)難是什么,以及維度減少算法如何與之抗衡,特別是當(dāng)多種假設(shè)成立的時(shí)候。那么接下來(lái)我們將一起學(xué)習(xí)一下常見的降維算法。
三. PCA(主成分分析
主成分分析(PCA)是目前最流行的降維算法。主要是通過(guò)識(shí)別與數(shù)據(jù)最接近的超平面,然后將數(shù)據(jù)投影到其上。
3.1 保持差異
在將訓(xùn)練集投影到較低維超平面之前,您首先需要選擇正確的超平面。例如,簡(jiǎn)單的2D數(shù)據(jù)集連同三個(gè)不同的軸(即一維超平面)一起在下圖的左側(cè)表示。右邊是將數(shù)據(jù)集投影到這些軸上的結(jié)果。正如你所看到的,在c2方向上的投影保留了最大的方差,而在c1上的投影保留了非常小的方差。
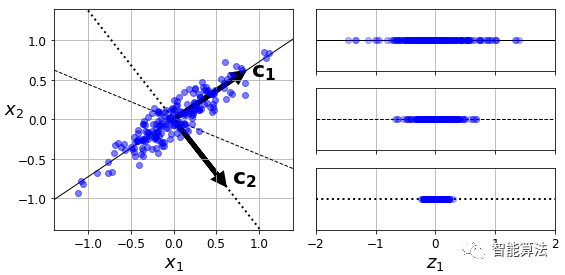
選擇保留最大變化量的軸似乎是合理的,因?yàn)樗钣锌赡軗p失比其他投影更少的信息。證明這一選擇的另一種方法是,使原始數(shù)據(jù)集與其在該軸上的投影之間的均方距離最小化的軸。這是PCA背后的一個(gè)相當(dāng)簡(jiǎn)單的想法。
3.2 PCA中的PC
主成分分析(PCA)識(shí)別訓(xùn)練集中變化量最大的軸。在上圖中,它是實(shí)線。它還發(fā)現(xiàn)第二個(gè)軸,與第一個(gè)軸正交,占了剩余方差的最大量。如果它是一個(gè)更高維的數(shù)據(jù)集,PCA也可以找到與前兩個(gè)軸正交的第三個(gè)軸,以及與數(shù)據(jù)集中維數(shù)相同的第四個(gè),第五個(gè)等。
定義第i個(gè)軸的單位矢量稱為第i個(gè)主成分(PC)。在上圖中,第一個(gè)PC是c1,第二個(gè)PC是c2。在2.1節(jié)的圖中,前兩個(gè)PC用平面中的正交箭頭表示,第三個(gè)PC與平面正交(指向上或下)。
主成分的方向不穩(wěn)定:如果稍微擾動(dòng)訓(xùn)練集并再次運(yùn)行PCA,一些新的PC可能指向與原始PC相反的方向。但是,他們通常仍然位于同一軸線上。在某些情況下,一部分的PC甚至可能旋轉(zhuǎn)或交換,但他們確定的平面通常保持不變。
那么怎樣才能找到訓(xùn)練集的主要組成部分呢?幸運(yùn)的是,有一種稱為奇異值分解(SVD)的標(biāo)準(zhǔn)矩陣分解方法,可以將訓(xùn)練集矩陣X分解成三個(gè)矩陣U·Σ·VT的點(diǎn)積,其中VT包含我們正在尋找的所有主成分, 如下公式所示。
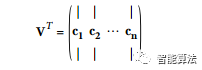
下面的Python代碼使用NumPy的svd()函數(shù)來(lái)獲取訓(xùn)練集的所有主成分,然后提取前兩個(gè)PC:

3.3 投影到d維度
一旦確定了所有主要組成部分,就可以將數(shù)據(jù)集的維數(shù)降至d維,方法是將其投影到由第一個(gè)主要組件定義的超平面上。選擇這個(gè)超平面確保投影將保留盡可能多的方差。例如,在2.1節(jié)中的數(shù)據(jù)集中,3D數(shù)據(jù)集向下投影到由前兩個(gè)主成分定義的2D平面,從而保留了大部分?jǐn)?shù)據(jù)集的方差。因此,二維投影看起來(lái)非常像原始的三維數(shù)據(jù)集。
為了將訓(xùn)練集投影到超平面上,可以簡(jiǎn)單地通過(guò)矩陣Wd計(jì)算訓(xùn)練集矩陣X的點(diǎn)積,該矩陣定義為包含前d個(gè)主分量的矩陣(即,由VT的前d列組成的矩陣 ),如下公式所示。
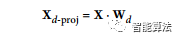
以下Python代碼將訓(xùn)練集投影到由前兩個(gè)主要組件定義的平面上:

現(xiàn)在我們已經(jīng)知道如何將任何數(shù)據(jù)集的維度降低到任意維數(shù),同時(shí)盡可能保留最多的差異。
3.4 使用Scikit-Learn
Scikit-Learn的PCA類使用SVD分解來(lái)實(shí)現(xiàn)PCA,就像我們之前做的那樣。以下代碼應(yīng)用PCA將數(shù)據(jù)集的維度降至兩維:

在將PCA變換器擬合到數(shù)據(jù)集之后,可以使用components_變量訪問(wèn)主成分(注意,它包含水平向量的PC,例如,第一個(gè)主成分等于pca.components_.T [:,0])。
3.5 解釋方差比率
另一個(gè)非常有用的信息是解釋每個(gè)主成分的方差比率,可通過(guò)explained_variance_ratio_變量得到。它指明了位于每個(gè)主成分軸上的數(shù)據(jù)集方差的比例。例如,讓我們看看圖8-2中表示的3D數(shù)據(jù)集的前兩個(gè)分量的解釋方差比率:

它告訴我們,84.2%數(shù)據(jù)集的方差位于第一軸,14.6%位于第二軸。第三軸的這一比例不到1.2%,所以可以認(rèn)為它可能沒有什么信息。
3.6 選擇正確的維度數(shù)量
不是任意選擇要減少的維度的數(shù)量,通常優(yōu)選選擇加起來(lái)到方差的足夠大部分(例如95%)的維度的數(shù)量。當(dāng)然,除非我們正在降低數(shù)據(jù)可視化的維度(在這種情況下,您通常會(huì)將維度降低到2或3)。
下面的代碼在不降低維數(shù)的情況下計(jì)算PCA,然后計(jì)算保留訓(xùn)練集方差的95%所需的最小維數(shù):

然后可以設(shè)置n_components = d并再次運(yùn)行PCA。但是,還有一個(gè)更好的選擇:不要指定要保留的主要組件的數(shù)量,您可以將n_components設(shè)置為0.0到1.0之間的浮點(diǎn)數(shù),表示您希望保留的方差比率:

3.7 PCA壓縮
降維后顯然,訓(xùn)練集占用的空間少得多。例如,嘗試將PCA應(yīng)用于MNIST數(shù)據(jù)集,同時(shí)保留其95%的方差。你會(huì)發(fā)現(xiàn)每個(gè)實(shí)例只有150多個(gè)特征,而不是原來(lái)的784個(gè)特征。所以,雖然大部分方差都被保留下來(lái),但數(shù)據(jù)集現(xiàn)在還不到原始大小的20%!這是一個(gè)合理的壓縮比,你可以看到這是如何加速分類算法(如SVM分類器)。
也可以通過(guò)應(yīng)用PCA投影的逆變換將縮小的數(shù)據(jù)集解壓縮回到784維。當(dāng)然這不會(huì)給你原來(lái)的數(shù)據(jù),因?yàn)橥队皝G失了一點(diǎn)信息(在5%的差異內(nèi)),但它可能會(huì)非常接近原始數(shù)據(jù)。原始數(shù)據(jù)與重構(gòu)數(shù)據(jù)(壓縮然后解壓縮)之間的均方距離稱為重建誤差。例如,以下代碼將MNIST數(shù)據(jù)集(公眾號(hào)回復(fù)“mnist”)壓縮到154維,然后使用inverse_transform()方法將其解壓縮到784維。下圖顯示了原始訓(xùn)練集(左側(cè))的幾個(gè)數(shù)字,以及壓縮和解壓縮后的相應(yīng)數(shù)字。你可以看到有一個(gè)輕微的圖像質(zhì)量損失,但數(shù)字仍然大部分完好無(wú)損。


如下等式,顯示了逆變換的等式。
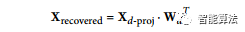
3.8 增量PCA
先于PCA實(shí)現(xiàn)的一個(gè)問(wèn)題是,為了使SVD算法運(yùn)行,需要整個(gè)訓(xùn)練集合在內(nèi)存中。幸運(yùn)的是,已經(jīng)開發(fā)了增量式PCA(IPCA)算法:您可以將訓(xùn)練集分成小批量,并一次只提供一個(gè)小批量IPCA算法。這對(duì)于大型訓(xùn)練集是有用的,并且也可以在線應(yīng)用PCA(即在新實(shí)例到達(dá)時(shí)即時(shí)運(yùn)行)。
下面的代碼將MNIST數(shù)據(jù)集分成100個(gè)小批量(使用NumPy的array_split()函數(shù)),并將它們提供給Scikit-Learn的IncrementalPCA class5,以將MNIST數(shù)據(jù)集的維度降低到154維(就像以前一樣)。請(qǐng)注意,您必須調(diào)用partial_fit()方法,而不是使用整個(gè)訓(xùn)練集的fit()方法。

或者,您可以使用NumPy的memmap類,它允許您操作存儲(chǔ)在磁盤上的二進(jìn)制文件中的大數(shù)組,就好像它完全在內(nèi)存中; 該類僅在需要時(shí)加載內(nèi)存中所需的數(shù)據(jù)。由于IncrementalPCA類在任何給定時(shí)間只使用數(shù)組的一小部分,因此內(nèi)存使用情況仍然受到控制。這可以調(diào)用通常的fit()方法,如下面的代碼所示:

3.9 隨機(jī)PCA
Scikit-Learn提供了另一種執(zhí)行PCA的選項(xiàng),稱為隨機(jī)PCA。這是一個(gè)隨機(jī)算法,可以快速找到前d個(gè)主成分的近似值,它比以前的算法快得多。

四. Kernel PCA
在前面的系列中,我們討論了內(nèi)核技巧,一種將實(shí)例隱式映射到非常高維的空間(稱為特征空間)的數(shù)學(xué)技術(shù),支持向量機(jī)的非線性分類和回歸。回想一下,高維特征空間中的線性決策邊界對(duì)應(yīng)于原始空間中的復(fù)雜非線性決策邊界。
事實(shí)證明,同樣的技巧可以應(yīng)用于PCA,使得有可能執(zhí)行復(fù)雜的非線性投影降維。這被稱為內(nèi)核PCA(KPCA)。在投影之后保留實(shí)例簇通常是好的,有時(shí)甚至可以展開靠近扭曲流形的數(shù)據(jù)集。
例如,以下代碼使用Scikit-Learn的KernelPCA類來(lái)執(zhí)行帶RBF內(nèi)核的KPCA(有關(guān)RBF內(nèi)核和其他內(nèi)核的更多詳細(xì)信息,可以參考前面的系列文章):

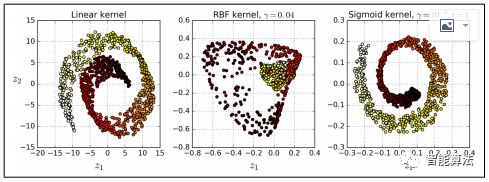
下圖顯示了使用線性內(nèi)核(等同于簡(jiǎn)單使用PCA類),RBF內(nèi)核和S形內(nèi)核(Logistic)減少到二維的瑞士卷。
五. LLE(局部線性嵌入)
局部線性嵌入(LLE)是另一種非常強(qiáng)大的非線性降維(NLDR)技術(shù)。這是一個(gè)流形學(xué)習(xí)技術(shù),不依賴于像以前的投影算法。簡(jiǎn)而言之,LLE通過(guò)首先測(cè)量每個(gè)訓(xùn)練實(shí)例如何與其最近的鄰居(c.n.)線性相關(guān),然后尋找保持這些本地關(guān)系最好的訓(xùn)練集的低維表示。這使得它特別擅長(zhǎng)展開扭曲的流形,尤其是在沒有太多噪聲的情況下。
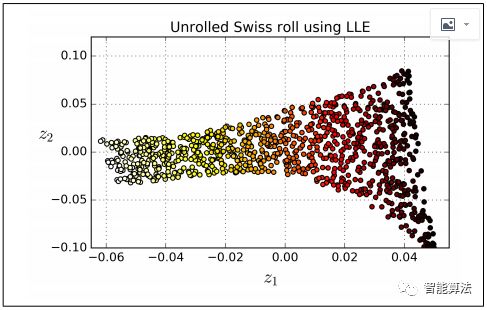
例如,下面的代碼使用Scikit-Learn的LocallyLinearEmbedding類來(lái)展開瑞士卷。得到的二維數(shù)據(jù)集如下圖所示。正如你所看到的,瑞士卷是完全展開的,實(shí)例之間的距離在本地保存得很好。但是,展開的瑞士卷的左側(cè)被擠壓,而右側(cè)的部分被拉長(zhǎng)。盡管如此,LLE在對(duì)多樣性進(jìn)行建模方面做得相當(dāng)不錯(cuò)。

六. 本期小結(jié)
本期我們從維度災(zāi)難入手,一起學(xué)習(xí)了降維的投影和流行分析的主要兩種途徑,接下來(lái)學(xué)習(xí)了主成分分析,核PCA以及LLE的相關(guān)知識(shí),希望從本節(jié)我們更詳細(xì)的了解到有關(guān)降維的相知識(shí),以及將其用到工作項(xiàng)目中。
(如需更好的了解相關(guān)知識(shí),歡迎加入智能算法社區(qū),在“智能算法”公眾號(hào)發(fā)送“社區(qū)”,即可加入算法微信群和QQ群)
本期代碼關(guān)鍵字:dim_redu
