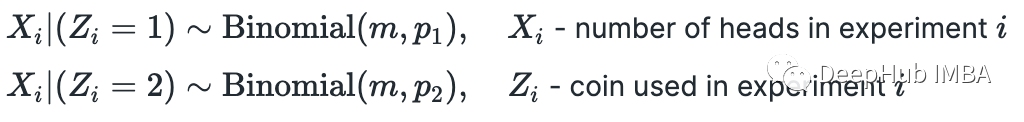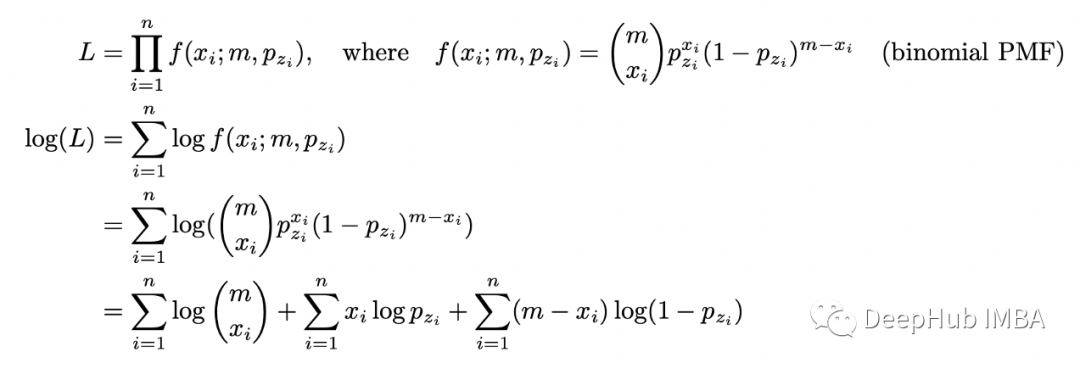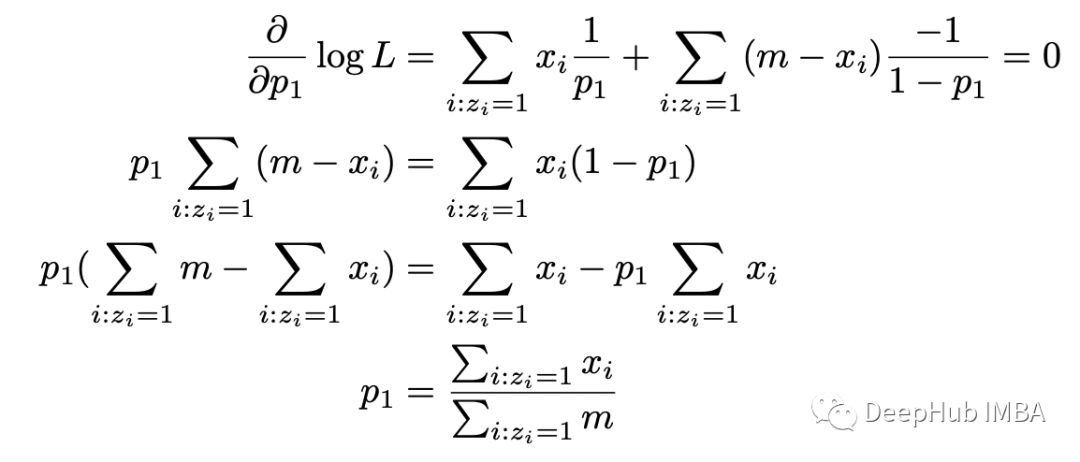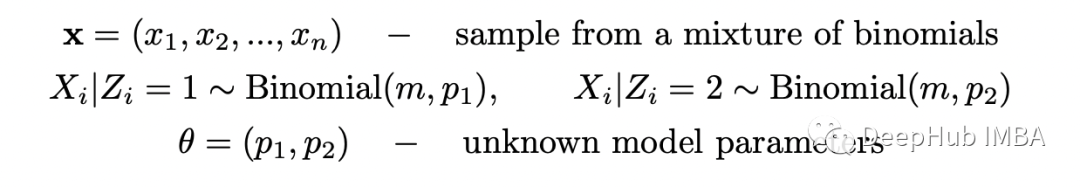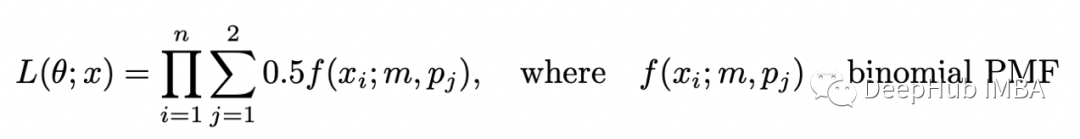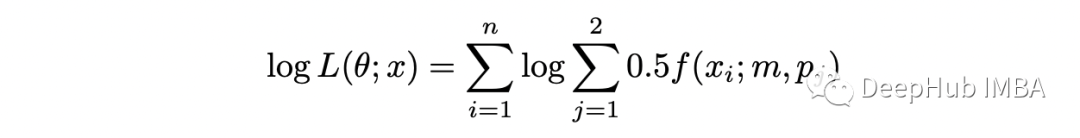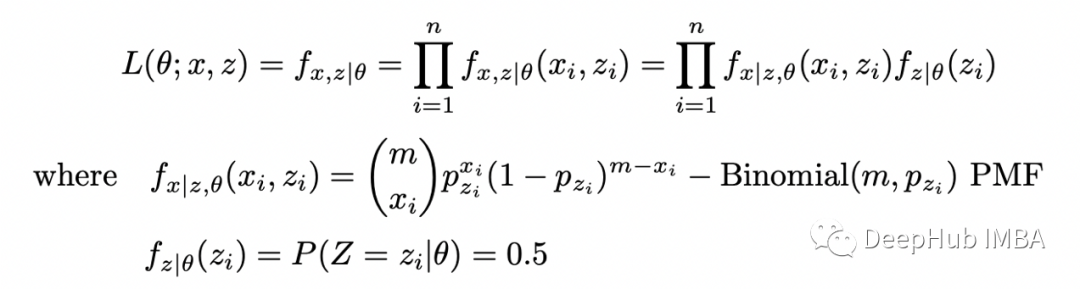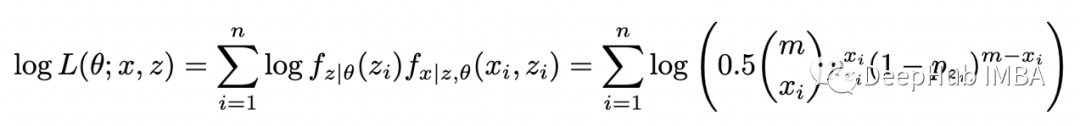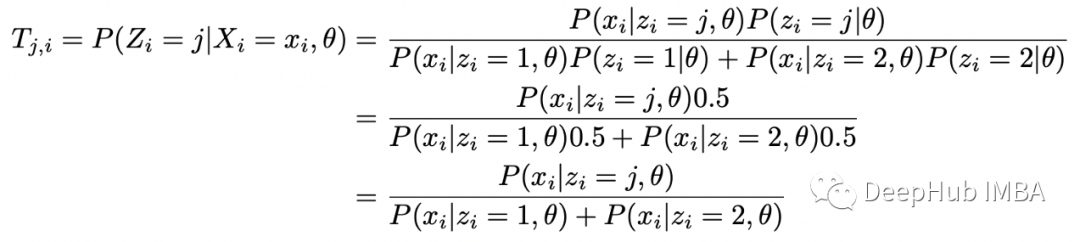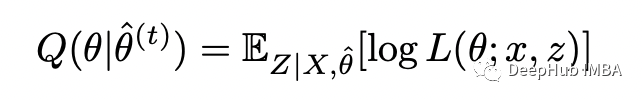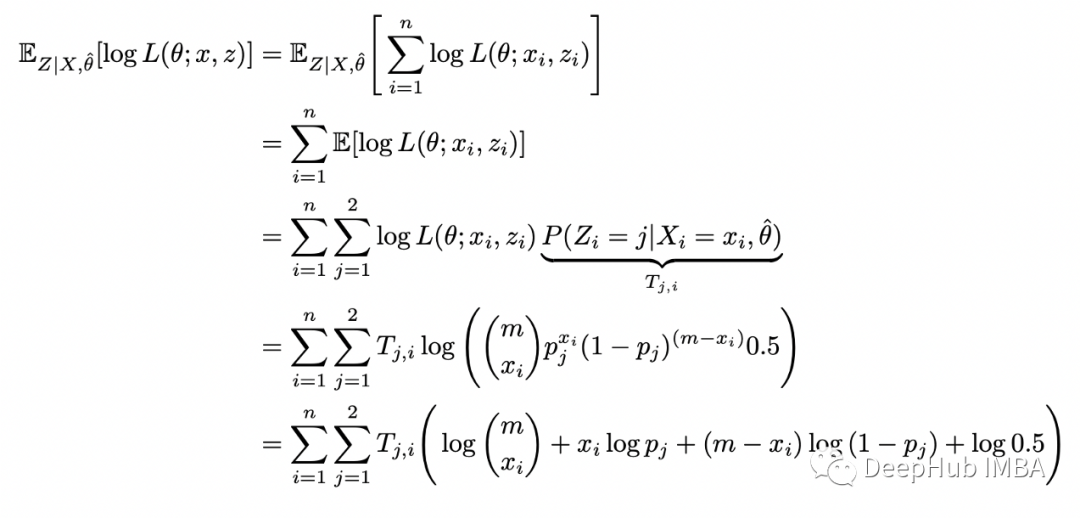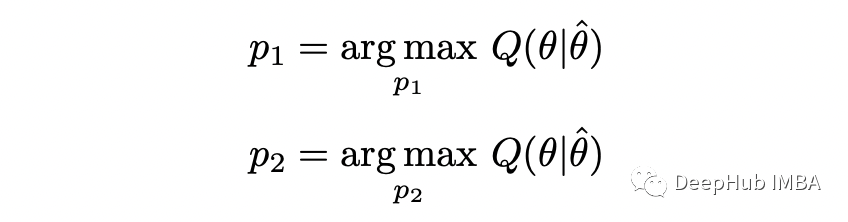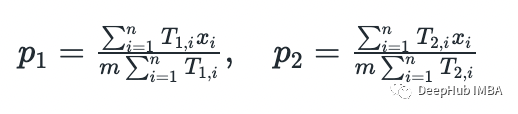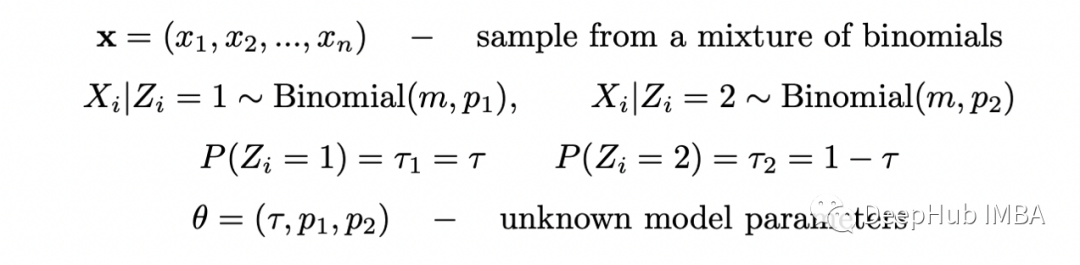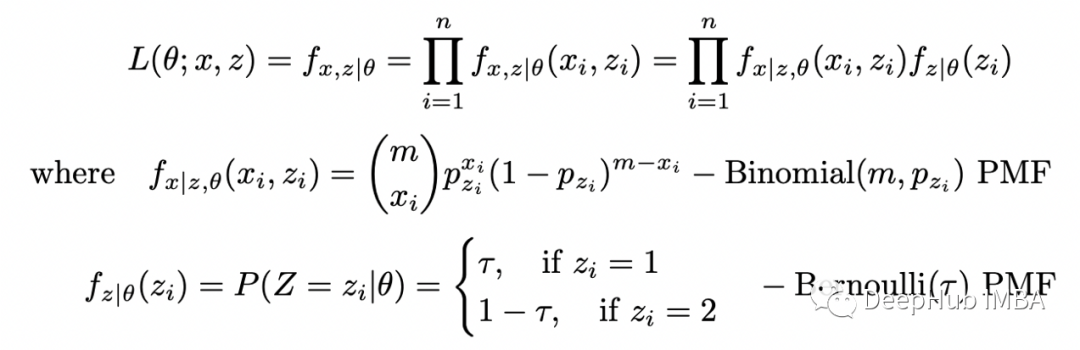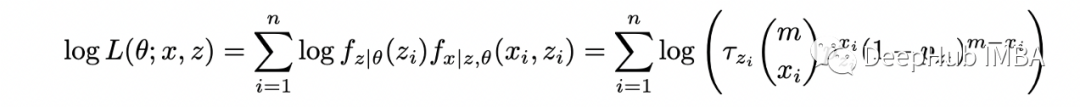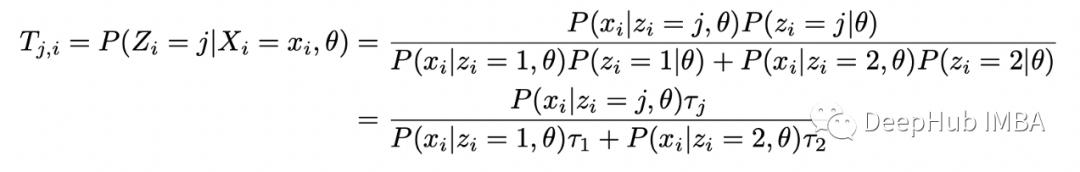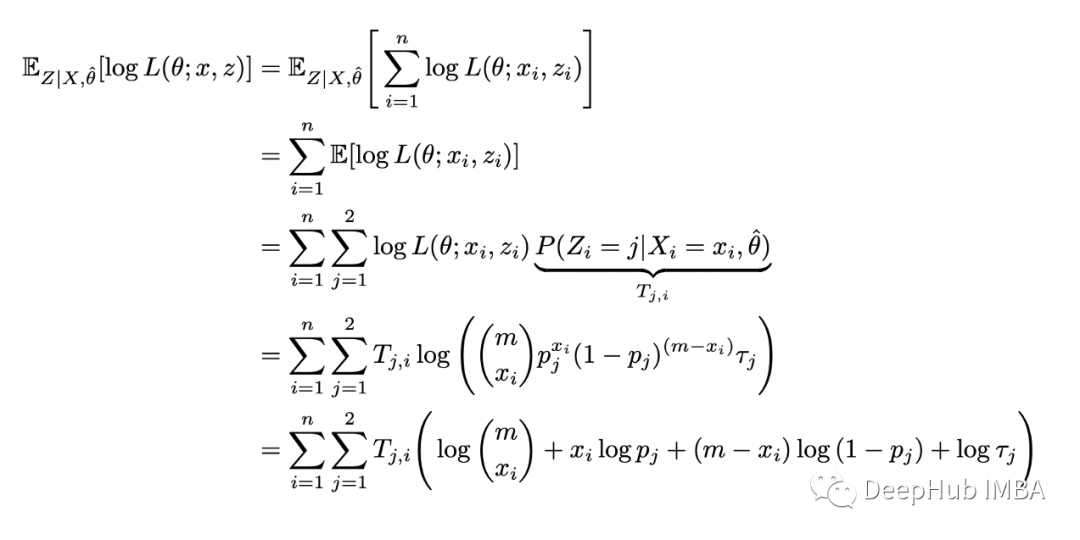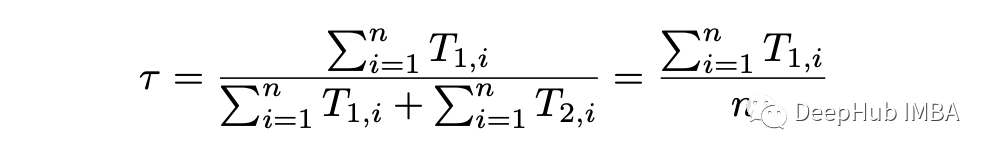本文約3400字,建議閱讀5分鐘
本文中通過(guò)幾個(gè)簡(jiǎn)單的示例解釋期望最大化算法是如何工作的。
期望最大化(EM)算法被廣泛用于估計(jì)不同統(tǒng)計(jì)模型的參數(shù)。它是一種迭代算法,可以將一個(gè)困難的優(yōu)化問(wèn)題分解為幾個(gè)簡(jiǎn)單的優(yōu)化問(wèn)題。在本文中將通過(guò)幾個(gè)簡(jiǎn)單的示例解釋它是如何工作的。這個(gè)算法最流行的例子(互聯(lián)網(wǎng)上討論最多的)可能來(lái)自這篇論文
(http://www.nature.com/nbt/journal/v26/n8/full/nbt1406.html)。這是一個(gè)非常簡(jiǎn)單的例子,所以我們也從這里開(kāi)始。
假設(shè)我們有兩枚硬幣(硬幣 1 和硬幣 2),正面朝上的概率不同。我們選擇其中一枚硬幣,翻轉(zhuǎn) m=10 并記錄正面的數(shù)量。假設(shè)我們重復(fù)這個(gè)實(shí)驗(yàn) n=5 次。我們的任務(wù)是確定每個(gè)硬幣正面朝上的概率。我們有:首先假設(shè)我們知道每個(gè)實(shí)驗(yàn)中使用了哪種硬幣。在這種情況下,有完整的信息,可以使用最大似然估計(jì) (MLE) 技術(shù)輕松求解 p_1 和 p_2。首先計(jì)算似然函數(shù)并取其對(duì)數(shù)(因?yàn)樽畲蠡瘜?duì)數(shù)似然函數(shù)更容易)。由于我們有 n 個(gè)獨(dú)立實(shí)驗(yàn),似然函數(shù)只是在 x_i 處評(píng)估的個(gè)體概率質(zhì)量函數(shù) (PMF) 的乘積(數(shù)字是實(shí)驗(yàn) i 中的正面)。
現(xiàn)在我們需要最大化關(guān)于概率 p_1 和 p_2 的對(duì)數(shù)似然函數(shù)。它可以在數(shù)值上或解析上完成。我將演示這兩種方法。首先讓我們嘗試解決它,可以分別求解 p_1 和 p_2。
對(duì) p_1 取對(duì)數(shù)似然函數(shù)的導(dǎo)數(shù),將其設(shè)置為零并求解 p_1。當(dāng)區(qū)分對(duì)數(shù)似然函數(shù)時(shí),涉及 p_2 的項(xiàng)的導(dǎo)數(shù)將等于 0。所以我們只使用涉及硬幣 1 的實(shí)驗(yàn)數(shù)據(jù)。得到的答案很直觀:它是我們?cè)谟矌?1 的實(shí)驗(yàn)中得到正面的總數(shù)除以硬幣 1 的實(shí)驗(yàn)中的翻轉(zhuǎn)總數(shù)。p_2 的計(jì)算將是類似的。
現(xiàn)在我將在 Python 中實(shí)現(xiàn)這個(gè)解決方案。m?=?10?
p_1 = 0.8p_2 = 0.3
xs = [] zs = [0,0,1,0,1]
np.random.seed(5)for i in zs: if i==0: xs.append(stats.binom(n=m, p=p_1).rvs()) elif i==1: xs.append(stats.binom(n=m, p=p_2).rvs()) xs = np.array(xs)print(xs)
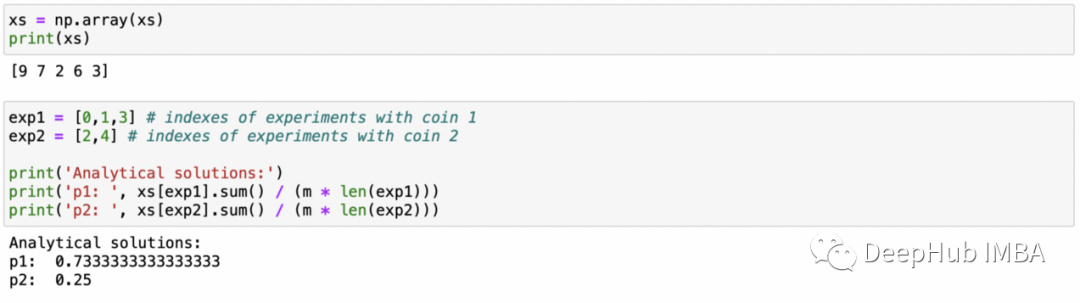
exp1 = [0,1,3] exp2 = [2,4]
print('Analytical solutions:')print('p1: ', xs[exp1].sum() / (m * len(exp1)))print('p2: ', xs[exp2].sum() / (m * len(exp2)))
這些實(shí)現(xiàn)都比較簡(jiǎn)單。我們只是實(shí)現(xiàn)上面計(jì)算的公式并插入數(shù)字。運(yùn)行此代碼的結(jié)果如下所示。解決這個(gè)問(wèn)題的另一種方法是使用數(shù)值求解器。我們需要找到一個(gè)最大化對(duì)數(shù)似然函數(shù)的解決方案,當(dāng)使用數(shù)值求解器時(shí),不需要計(jì)算導(dǎo)數(shù)并手動(dòng)求解最大化對(duì)數(shù)似然函數(shù)的參數(shù)。只需實(shí)現(xiàn)一個(gè)我們想要最大化的函數(shù)并將其傳遞給數(shù)值求解器。
由于 Python 中的大多數(shù)求解器旨在最小化給定函數(shù),因此我們實(shí)現(xiàn)了一個(gè)計(jì)算負(fù)對(duì)數(shù)似然函數(shù)的函數(shù)(因?yàn)樽钚』?fù)對(duì)數(shù)似然函數(shù)與最大化對(duì)數(shù)似然函數(shù)相同)。ef neg_log_likelihood(probs, m, xs, zs): ''' compute negative log-likelihood ''' ll = 0 for x,z in zip(xs,zs): ll += stats.binom(p=probs[z], n=m).logpmf(x) return -ll res = optimize.minimize(neg_log_likelihood, [0.5,0.5], bounds=[(0,1),(0,1)], args=(m,xs,zs), method='tnc')
print('Numerical solution:')print('p1: ', res.x[0])print('p2: ', res.x[1])
和上面的第一種方法得到與解析解相同的結(jié)果。
現(xiàn)在假設(shè)我們不知道每個(gè)實(shí)驗(yàn)中使用了哪種硬幣。在這種情況下,變量 Z 沒(méi)有被觀察到(它被稱為潛在變量或隱藏變量)并且數(shù)據(jù)集變得不完整。現(xiàn)在估計(jì)概率 p_1 和 p_2 變得更加困難,但仍然可以在 EM 算法的幫助下完成。如果知道選擇硬幣 1 或硬幣 2 的概率,就可以使用貝葉斯定理來(lái)估計(jì)每個(gè)硬幣的偏差。如果知道每個(gè)硬幣的偏差,可以估計(jì)在給定的實(shí)驗(yàn)中使用硬幣 1 或硬幣 2 的概率。在 EM 算法中,我們對(duì)這些概率進(jìn)行初步猜測(cè),然后在兩個(gè)步驟之間迭代(估計(jì)偏差給定使用每個(gè)硬幣的概率和估計(jì)使用每個(gè)硬幣給定偏差的概率)直到收斂。可以在數(shù)學(xué)上證明這種算法收斂到(似然函數(shù)的)局部最大值。現(xiàn)在嘗試復(fù)制論文中提供的示例。問(wèn)題設(shè)置如下所示。完整的數(shù)據(jù)集由兩個(gè)變量 X 和 Z 組成,但僅觀察到 X。由于隨機(jī)選擇兩個(gè)硬幣中的一個(gè),因此選擇每個(gè)硬幣的概率等于 0.5。為了求解 theta,我們需要最大化以下似然函數(shù):
上述函數(shù)稱為不完全似然函數(shù)。如果我們計(jì)算它的對(duì)數(shù),我們得到:
對(duì)數(shù)下的求和使最大化問(wèn)題變得困難。
讓我們將隱藏變量 Z 包含在似然函數(shù)中以獲得完全似然:完全似然函數(shù)的對(duì)數(shù)為:
這樣就沒(méi)有對(duì)數(shù)內(nèi)的求和,更容易解決這個(gè)函數(shù)的最大化問(wèn)題。由于沒(méi)有觀察到 Z 的值,所以不能直接計(jì)算和最大化這個(gè)函數(shù)。但是如果我們知道 Z 的分布,就可以計(jì)算其期望值并使用它來(lái)最大化似然(或?qū)?shù)似然)函數(shù)。
這里的問(wèn)題是,要找到 Z 的分布,需要知道參數(shù) theta,而要找到參數(shù) theta,需要知道 Z 的分布。EM 算法允許我們解決這個(gè)問(wèn)題。我們從參數(shù) theta 的隨機(jī)猜測(cè)開(kāi)始,然后迭代以下步驟:- 期望步驟(E-step):計(jì)算完整對(duì)數(shù)似然函數(shù)相對(duì)于 Z 給定數(shù)據(jù) X 的當(dāng)前條件分布和當(dāng)前參數(shù)估計(jì) theta 的條件期望;
- 最大化步驟(M-step):找到最大化該期望的參數(shù) theta 的值。
可以使用貝葉斯定理在給定 X_i 和 theta 的情況下找到 Z_i 的條件分布:現(xiàn)在定義完全對(duì)數(shù)似然的條件期望如下:
插入完整的對(duì)數(shù)似然函數(shù)并重新排列:
這樣就完成了 E-step。在 M-step中,我們根據(jù)參數(shù) theta 最大化上面計(jì)算的函數(shù):
在這個(gè)的示例中,可以通過(guò)分析找到參數(shù)(通過(guò)求導(dǎo)并將其設(shè)置為零)。這里就不演示整個(gè)過(guò)程,只是提供答案。
在下面的實(shí)現(xiàn)中將使用與論文中相同數(shù)據(jù)來(lái)檢查是否獲得了相同的結(jié)果。Python 代碼如下:
m = 10 # number of flips in each samplen = 5 # number of samplesxs = np.array([5,9,8,4,7])
theta = [0.6, 0.5] # initial guess p_1, p_2
for i in range(10): p_1,p_2 = theta T_1s = [] T_2s = [] for x in xs: T_1 = stats.binom(n=m,p=theta[0]).pmf(x) / (stats.binom(n=m,p=theta[0]).pmf(x) + stats.binom(n=m,p=theta[1]).pmf(x)) T_2 = stats.binom(n=m,p=theta[1]).pmf(x) / (stats.binom(n=m,p=theta[0]).pmf(x) + stats.binom(n=m,p=theta[1]).pmf(x)) T_1s.append(T_1) T_2s.append(T_2) T_1s = np.array(T_1s) T_2s = np.array(T_2s) p_1 = np.dot(T_1s, xs) / (m * np.sum(T_1s)) p_2 = np.dot(T_2s, xs) / (m * np.sum(T_2s)) print(f'step:{i}, p1={p_1:.2f}, p2={p_2:.2f}') theta = [p_1, p_2]
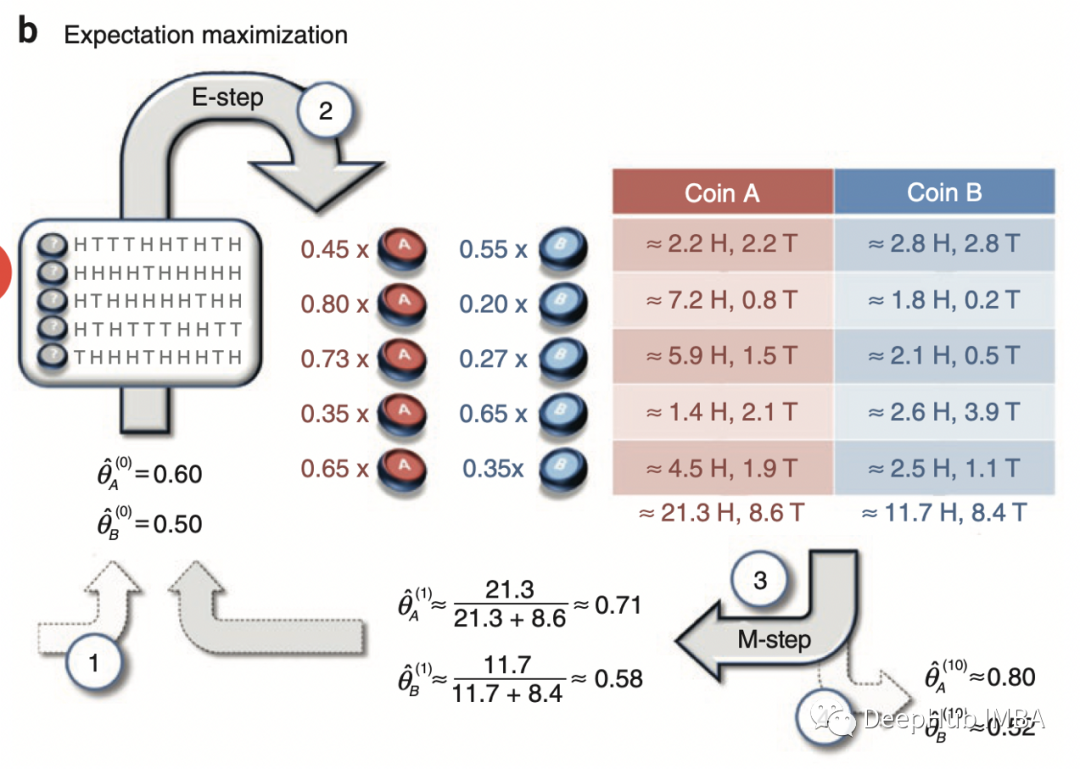
所有參數(shù)與論文中的完全相同。下面可以看到論文中的圖表和上面代碼的輸出。結(jié)果與論文中完全相同,這意味著 EM 算法的實(shí)現(xiàn)是正確的。也可以使用數(shù)值求解器來(lái)最大化完全對(duì)數(shù)似然函數(shù)的條件期望,但在這種情況下使用解析解更容易。現(xiàn)在讓我們?cè)囍寙?wèn)題變得更復(fù)雜一些。假設(shè)選擇每個(gè)硬幣的概率是未知的。那么我們將有兩個(gè)二項(xiàng)式的混合,選擇第一個(gè)硬幣的概率為 tau,選擇第二個(gè)硬幣的概率為 1-tau。我們重復(fù)與之前相同的步驟。定義完全似然函數(shù):
在前面的例子中,給定 theta 的 Z 的條件概率是恒定的,現(xiàn)在它是帶有參數(shù) tau 的伯努利分布的 PMF。
計(jì)算完整的對(duì)數(shù)似然函數(shù):求給定 X 和 theta 的隱藏變量 Z 的條件分布:
計(jì)算對(duì)數(shù)似然的條件期望:
剩下的就是最大化關(guān)于參數(shù) theta 的條件期望。上式中涉及概率 p_j 的項(xiàng)與之前的完全一樣,所以 p_1 和 p_2 的解是相同的。最大化關(guān)于 tau 的條件期望,可以得到:
Python 中實(shí)現(xiàn)這個(gè)算法的代碼如下p_1 = 0.1p_2 = 0.8tau_1 = 0.3tau_2 = 1-tau_1
m = 10 # number of flips in each samplen = 10 # number of samples
np.random.seed(123)dists = [stats.binom(n=m, p=p_1), stats.binom(n=m, p=p_2)]xs = [dists[x].rvs() for x in np.random.choice([0,1], size=n, p=[tau_1,tau_2])]
np.random.seed(123)theta = [np.random.rand() for _ in range(3)]
last_ll = 0max_iter = 100
for i in range(max_iter): tau,p_1,p_2 = theta T_1s = [] T_2s = [] lls = [] for x in xs: denom = (tau * stats.binom(n=m,p=p_1).pmf(x) + (1-tau) * stats.binom(n=m,p=p_2).pmf(x)) T_1 = tau * stats.binom(n=m,p=p_1).pmf(x) / denom T_2 = (1-tau) * stats.binom(n=m,p=p_2).pmf(x) / denom T_1s.append(T_1) T_2s.append(T_2) lls.append(T_1 * np.log(tau * stats.binom(n=m,p=p_1).pmf(x)) + T_2 * np.log(tau * stats.binom(n=m,p=p_2).pmf(x))) T_1s = np.array(T_1s) T_2s = np.array(T_2s) tau = np.sum(T_1s) / n p_1 = np.dot(T_1s, xs) / (m * np.sum(T_1s)) p_2 = np.dot(T_2s, xs) / (m * np.sum(T_2s)) print(f'step:{i}, tau={tau}, p1={p_1:.2f}, p2={p_2:.2f}, log_likelihood={sum(lls):.2f}') theta = [tau, p_1, p_2] if abs(sum(lls) - last_ll) < 0.001: break else: last_ll=sum(lls)
在前面的示例中,將算法運(yùn)行了 10 次迭代,復(fù)制論文中的結(jié)果。但是在實(shí)踐中,我們運(yùn)行算法直到收斂,這意味著當(dāng)對(duì)數(shù)似然停止改進(jìn)時(shí)就停止算法。算法的輸出如上所示。由于問(wèn)題的對(duì)稱性,p_1 和 p_2 的概率被調(diào)換了但 結(jié)果仍然是正確的并且接近參數(shù)的真實(shí)值:我們有 p=0.85,概率為 0.8,p=0.1,概率為 0.2(真實(shí)值:p=0.8,概率為 0.7,p=0.1,概率為 0.3)。
本文的目的是通過(guò)一些簡(jiǎn)單的示例演示 EM 算法的基礎(chǔ)知識(shí)。https://github.com/financialnoob/misc/blob/305bf8bc7cbdddaf47d40078100ba27935ff4452/6.introduction_to_em_algorithm.ipynb