圖解：什么是AVL樹(shù)？（刪除總結(jié)篇）

來(lái)源：景禹

作者：景禹

上一篇文章討論了平衡二叉樹(shù)的插入操作，沒(méi)有看的可以去看一下 圖解：什么是AVL樹(shù)？，有助于理解今天要講的平衡二叉樹(shù)的刪除操作。

平衡二叉樹(shù)的刪除操作與插入操作類似，先執(zhí)行標(biāo)準(zhǔn)的BST刪除操作（可以參考文章 圖解：什么是二叉排序樹(shù)？ ），然后進(jìn)行相應(yīng)的平衡操作。而平衡操作最基本的兩個(gè)步驟就是左旋和右旋，如下圖所示：

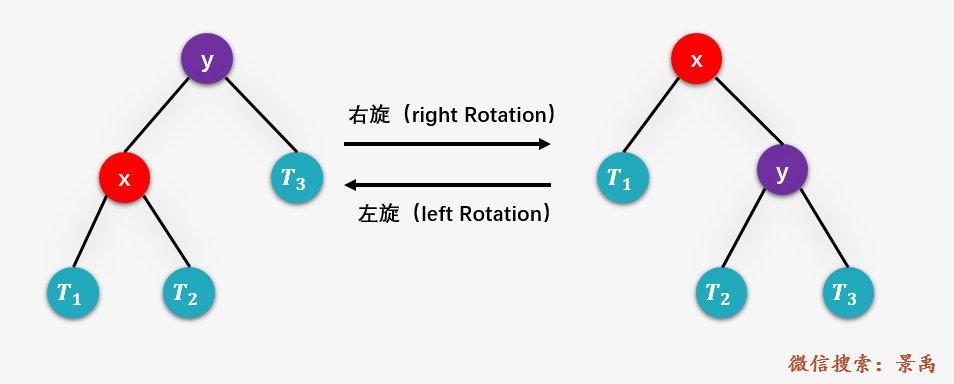
平衡二叉樹(shù)的刪除操作

與平衡二叉樹(shù)的插入操作類似，我們以刪除一個(gè)結(jié)點(diǎn) 為例進(jìn)行說(shuō)明平衡二叉樹(shù)刪除操作的具體算法步驟。

1. 對(duì)結(jié)點(diǎn) 執(zhí)行標(biāo)準(zhǔn)的二叉排序樹(shù)的刪除操作；
2. 從結(jié)點(diǎn) 開(kāi)始，向上回溯，找到第一個(gè)不平衡的結(jié)點(diǎn)（即平衡因子不是 -1，0或1的結(jié)點(diǎn)） ； 為結(jié)點(diǎn) 的高度最高的孩子結(jié)點(diǎn)； 是結(jié)點(diǎn) 的高度最高的孩子結(jié)點(diǎn)（ 這里一定注意和平衡二叉樹(shù)插入操作區(qū)分開(kāi)來(lái)，y不再是從w回溯到z的路徑上z的孩子，x也不再是z的孫子這樣的描述，一定要注意奧！！！ ）。
3. 然后對(duì)以 為根結(jié)點(diǎn)的子樹(shù)進(jìn)行平衡操作，其中 x、y、z 可以的位置有四種情況，BST刪除操作之后的平衡操作也就處理以下四種情況：
• y 是 z 的左孩子，x 是 y 的左孩子 （Left Left ，LL )；
• y 是 z 的左孩子，x 是 y 的右孩子 （Left Right ，LR )；
• y 是 z 的右孩子，x 是 y 的右孩子 （Right Right ，RR )；
• y 是 z 的右孩子，x 是 y 的左孩子 （Right Right ，RL )；

這里的四種情況與插入操作一樣，但需要注意的是，插入操作僅需要對(duì)以 z 為根的子樹(shù)進(jìn)行平衡操作；而平衡二叉樹(shù)的刪除操作就不一樣，先對(duì)以 z 為根的子樹(shù)進(jìn)行平衡操作，之后可能需要對(duì) z 的祖先結(jié)點(diǎn)進(jìn)行平衡操作，向上回溯直到根結(jié)點(diǎn)。

第一種情況：LL

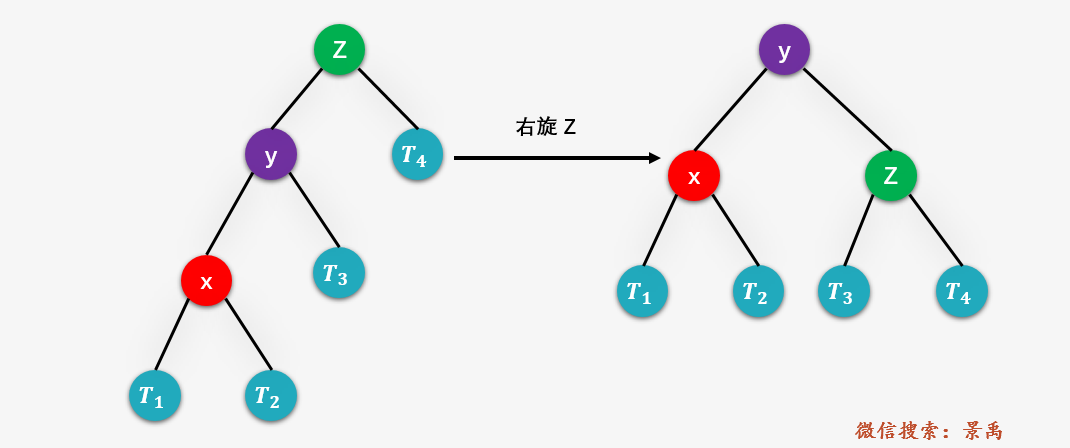
第二種情況：LR

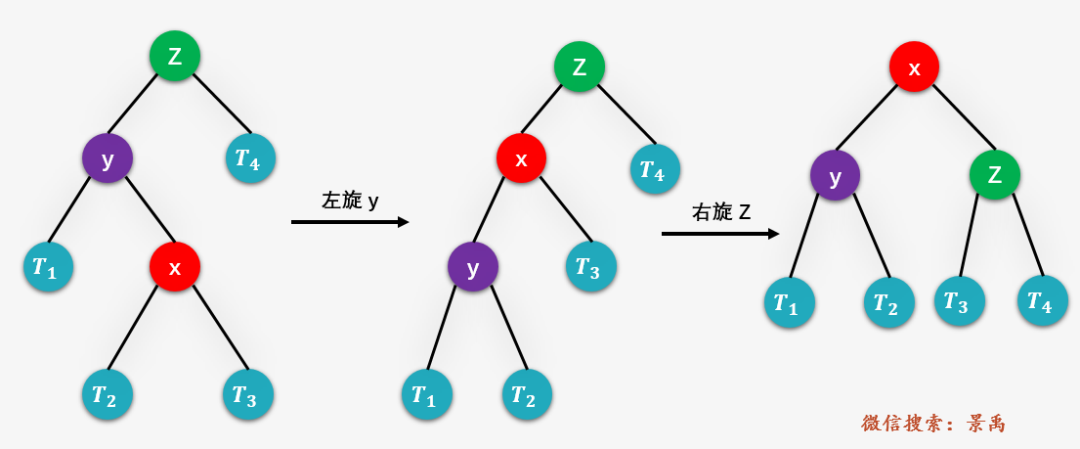
第三種情況：RR

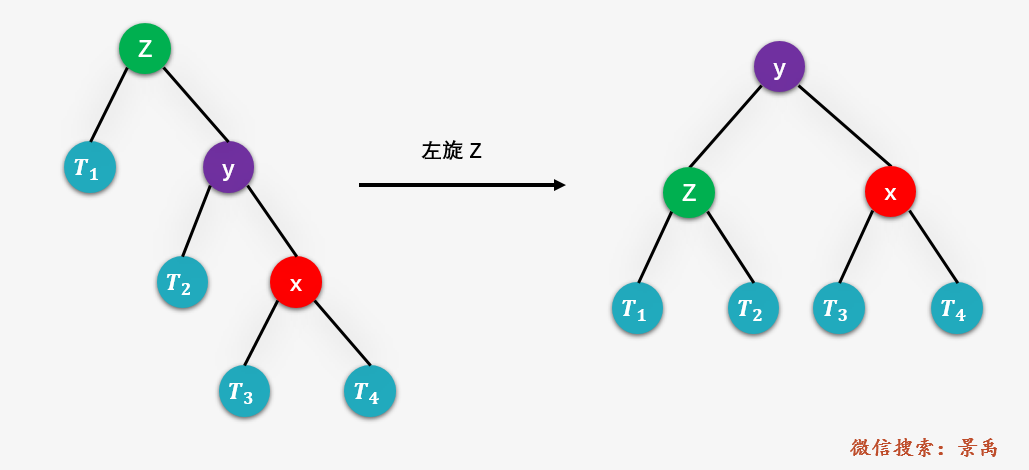
第四種情況：RL

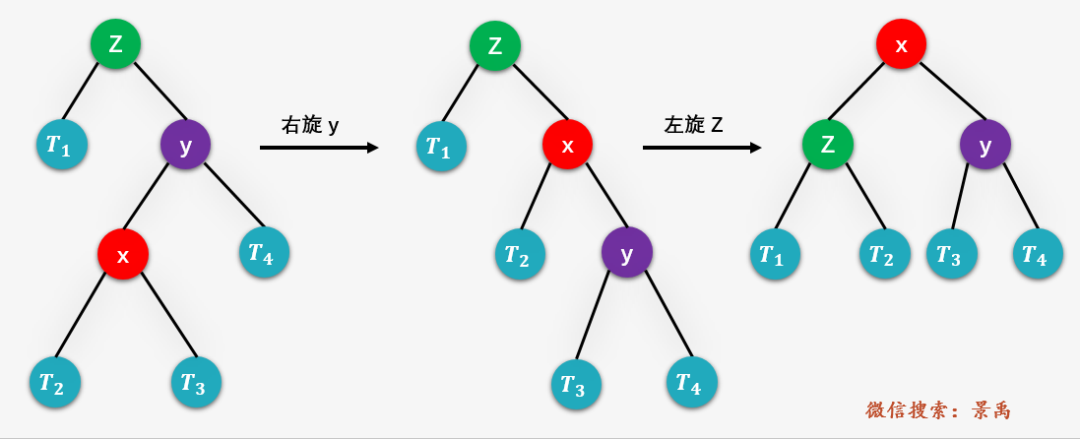
舉例說(shuō)明

示例一：

我們已刪除下圖中的結(jié)點(diǎn) 32 為例進(jìn)行說(shuō)明。

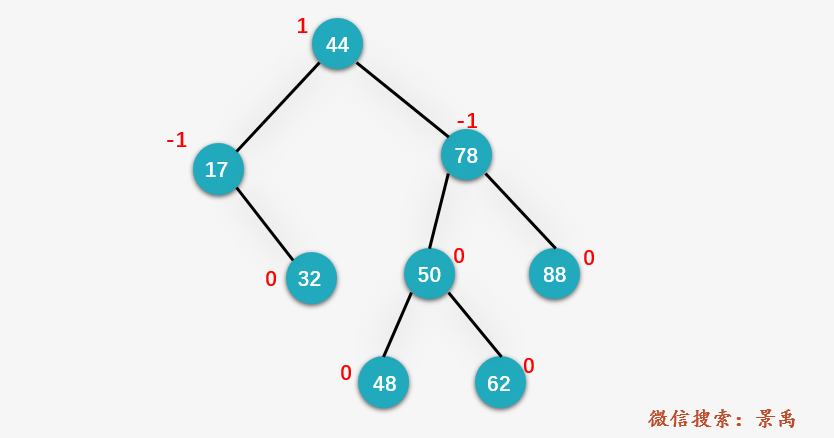
第一步：由于 32 結(jié)點(diǎn)為葉子結(jié)點(diǎn)，直接刪除，并保存刪除結(jié)點(diǎn)的父節(jié)點(diǎn) 17 。

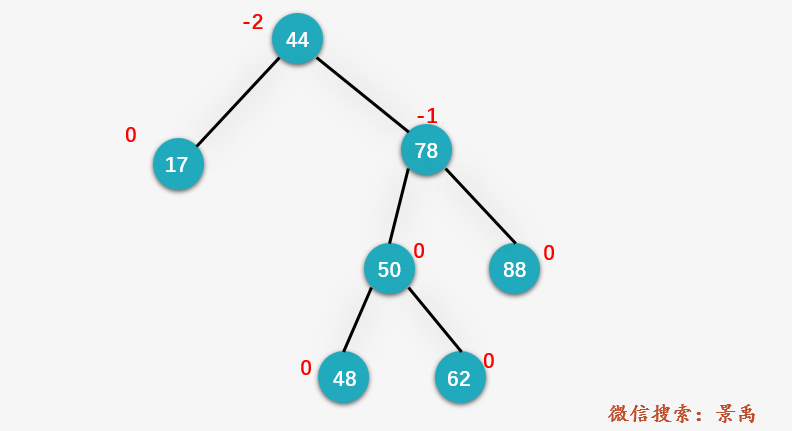第二步：從節(jié)點(diǎn) 17 向上回溯，找到第一個(gè)不平衡結(jié)點(diǎn) 44 ，并找到不平衡結(jié)點(diǎn)的左右孩子中深度最深的結(jié)點(diǎn) 78 （即 y ）；以及 y 的孩子結(jié)點(diǎn)當(dāng)中深度最深的結(jié)點(diǎn) 50 （即 x ）。 發(fā)現(xiàn)為 RL 的情況。

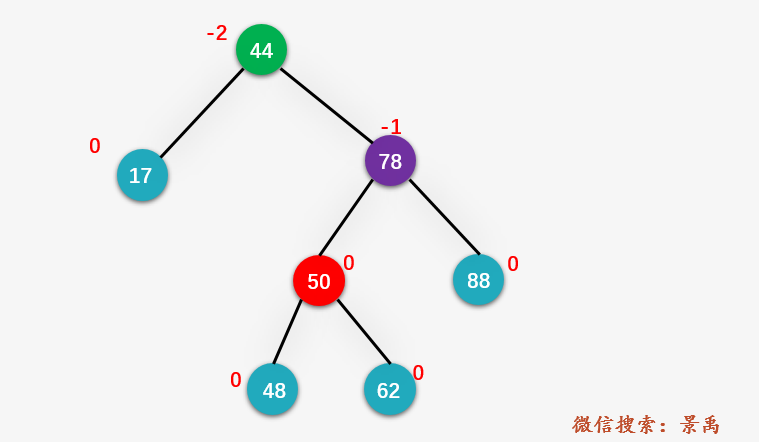
第三步：對(duì)結(jié)點(diǎn) 78 進(jìn)行右旋操作

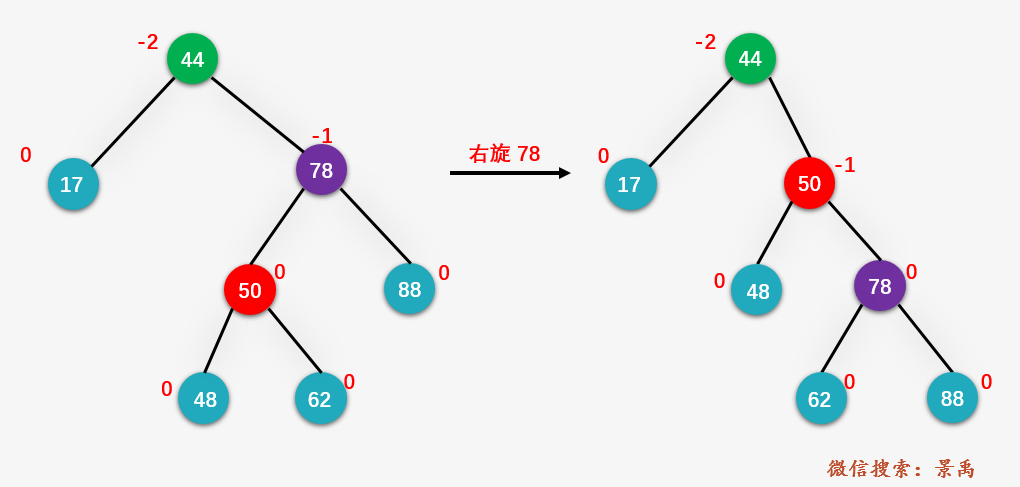第四步：對(duì)結(jié)點(diǎn) 44 進(jìn)行左旋操作

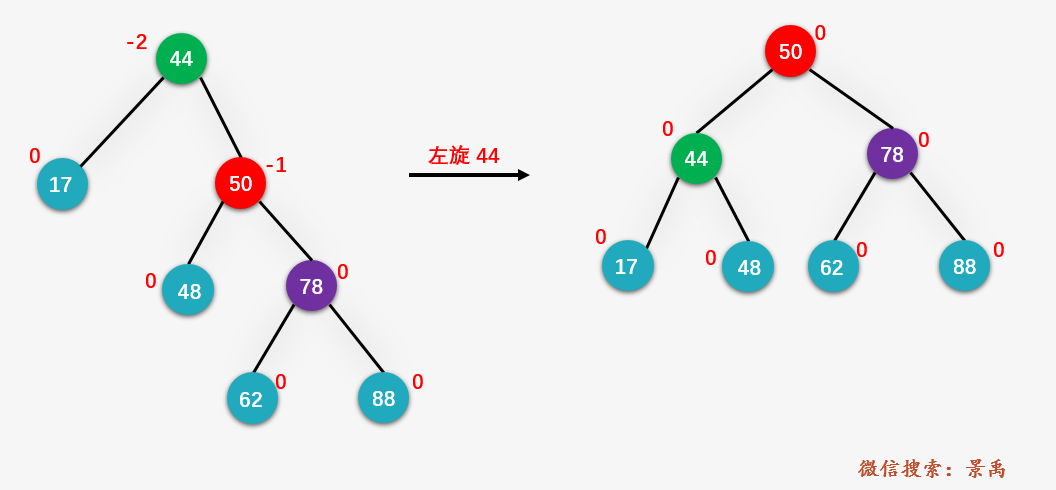
示例二

我們以刪除下圖中的結(jié)點(diǎn) 80 為例進(jìn)行說(shuō)明。

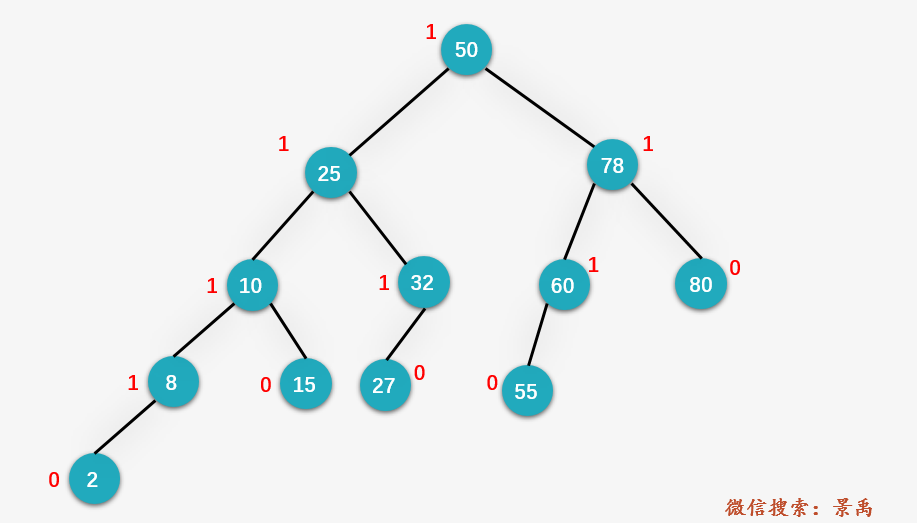
第一步，由于結(jié)點(diǎn) 80 為葉子結(jié)點(diǎn)，則直接刪除，并保存結(jié)點(diǎn) 80 的父結(jié)點(diǎn) 78 。

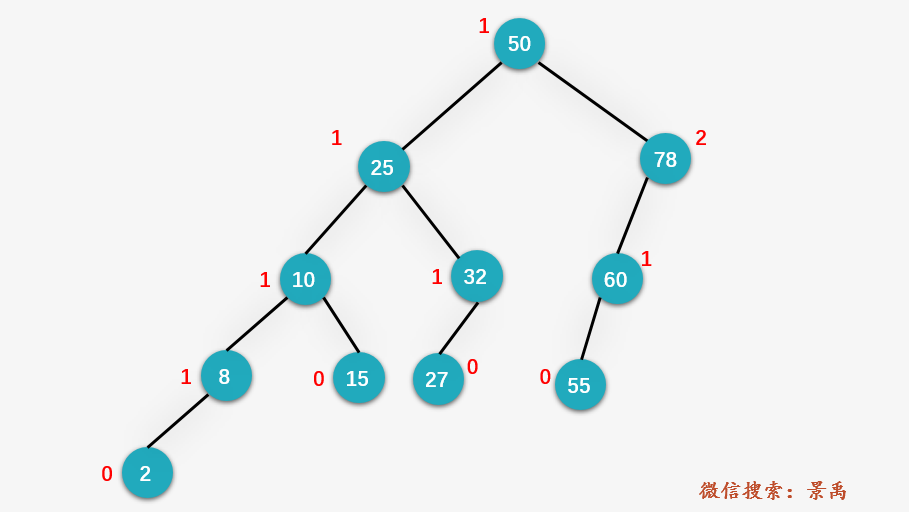
第二步：從結(jié)點(diǎn) 78 開(kāi)始尋找第一個(gè)不平衡結(jié)點(diǎn)，發(fā)現(xiàn)就是結(jié)點(diǎn) 78 本身（即結(jié)點(diǎn) z ），找到結(jié)點(diǎn) 78 深度最深的葉子結(jié)點(diǎn) 60 （即結(jié)點(diǎn) y ），以及結(jié)點(diǎn) y 的深度最深的葉結(jié)點(diǎn) 55 （即結(jié)點(diǎn) x ）。即 LL 的情況。

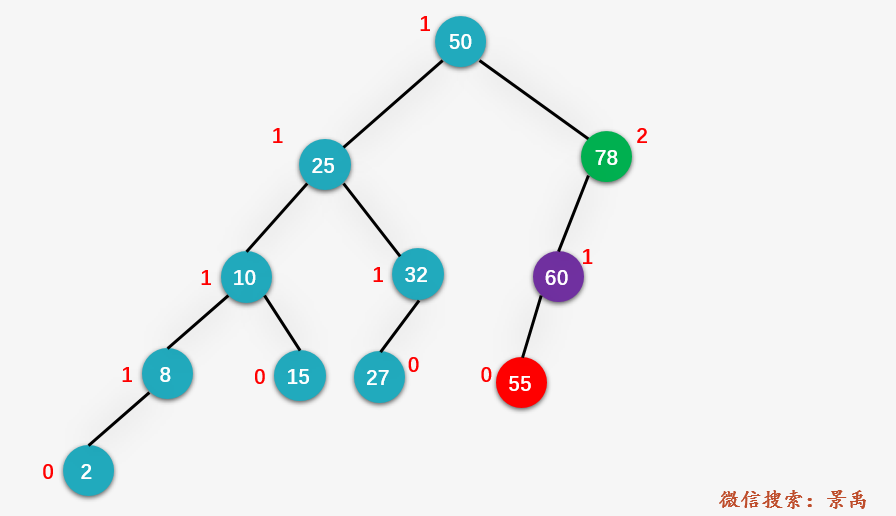
第三步：右旋結(jié)點(diǎn) 78

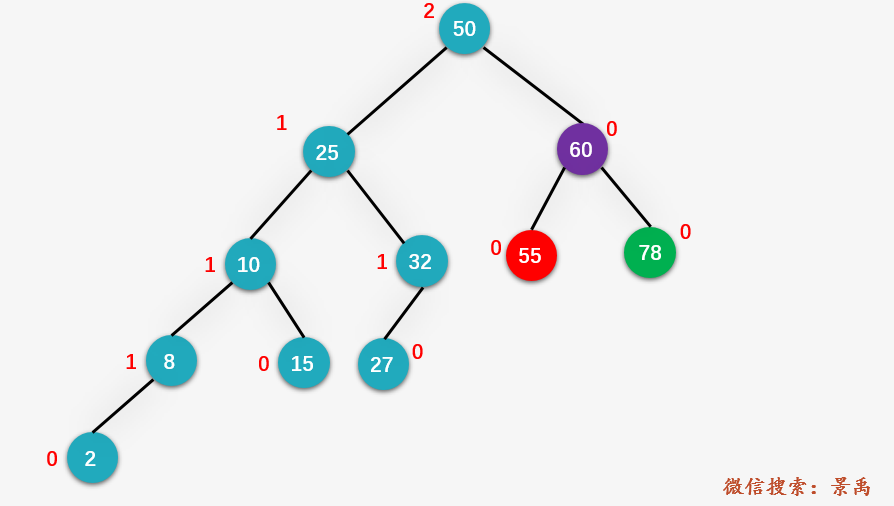
第四步：從旋轉(zhuǎn)后的返回的新的根結(jié)點(diǎn) 60 向上回溯（這里就和平衡二叉樹(shù)的插入操作有別了奧，平衡二叉樹(shù)的插入操作僅對(duì)第一個(gè)不平衡結(jié)點(diǎn)的子樹(shù)進(jìn)行平衡操作，而AVL的刪除需要不斷地回溯，直到根結(jié)點(diǎn)平衡為止 ），判斷是否還有不平衡結(jié)點(diǎn)，發(fā)現(xiàn)整棵樹(shù)的根結(jié)點(diǎn) 50 為第一個(gè)不平衡結(jié)點(diǎn)，找到對(duì)應(yīng)的 y 結(jié)點(diǎn) 25 和 x 結(jié)點(diǎn) 10 。同樣是 LL 的情況。

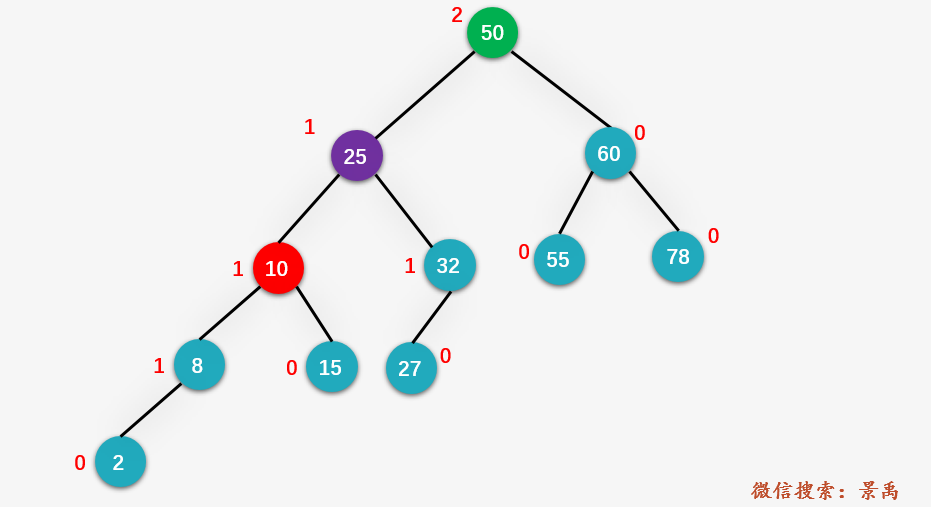
第五步：對(duì) z 結(jié)點(diǎn) 50 進(jìn)行右旋操作。

平衡二叉樹(shù)的優(yōu)缺點(diǎn)分析

優(yōu)點(diǎn)

平衡二叉樹(shù)的優(yōu)點(diǎn)不言而喻，相對(duì)于二叉排序樹(shù)（BST）而言，平衡二叉樹(shù)避免了二叉排序樹(shù)可能出現(xiàn)的最極端情況（斜樹(shù)）問(wèn)題，其平均查找的時(shí)間復(fù)雜度為 .

缺點(diǎn)

很遺憾，平衡二叉樹(shù)為了保持平衡，動(dòng)態(tài)進(jìn)行插入和刪除操作的代價(jià)也會(huì)增加。因此出現(xiàn)了后來(lái)的紅黑樹(shù)，過(guò)兩天景禹自會(huì)抽時(shí)間講解。

時(shí)間復(fù)雜度分析

左旋和右旋操作僅需要改變幾個(gè)指針，時(shí)間復(fù)雜度為 ，更新結(jié)點(diǎn)的深度以及獲得平衡因子僅需要常數(shù)時(shí)間，所以平衡二叉樹(shù)AVL的刪除操作的時(shí)間復(fù)雜度與二叉排序樹(shù)BST的刪除操作一樣，均為 ，其中 h 為樹(shù)的高度。由于AVL 樹(shù)是平衡的，所以高度 ，因此，AVL 刪除操作的時(shí)間復(fù)雜度為 .

平衡二叉樹(shù)的刪除操作實(shí)現(xiàn)

關(guān)于左旋與右旋操作，以及平衡因子的計(jì)算與之前講的文章 圖解：什么是AVL樹(shù)？ 中的實(shí)現(xiàn)是一致的，我們直接看AVL刪除操作的實(shí)現(xiàn)代碼：

//返回刪除指定結(jié)點(diǎn)后的平衡二叉樹(shù)的根結(jié)點(diǎn)
struct?Node*?deleteNode(struct?Node*?root,?int?key)?
{?
?//?步驟一:?標(biāo)準(zhǔn)的BST刪除操作

?if?(root?==?NULL)?
??return?root;?

?//如果要?jiǎng)h除的結(jié)點(diǎn)的key小于root->key
?//則表示該結(jié)點(diǎn)位于左子樹(shù)當(dāng)中，遞歸遍歷左子樹(shù)
?if?(?key?key?)?
??root->left?=?deleteNode(root->left,?key);?

?//如果要?jiǎng)h除的結(jié)點(diǎn)的key大于root->key
?//則表示該結(jié)點(diǎn)位于右子樹(shù)當(dāng)中，遞歸遍歷右子樹(shù)
?else?if(?key?>?root->key?)?
??root->right?=?deleteNode(root->right,?key);?

?//找到刪除結(jié)點(diǎn)，進(jìn)行刪除操作
?else
?{?
??//?被刪除結(jié)點(diǎn)只有一個(gè)孩子或者沒(méi)有孩子，
??if(?(root->left?==?NULL)?||?(root->right?==?NULL)?)?
??{?
???struct?Node?*temp?=?root->left???root->left?:?
???????????root->right;?

???//?temp為空，左右孩子均為空
???if?(temp?==?NULL)?
???{?
????temp?=?root;?
????root?=?NULL;?
???}?
???else?//?僅有一個(gè)孩子
????*root?=?*temp;?//拷貝非空孩子

???free(temp);?
??}?
??else
??{?
???//?被刪除結(jié)點(diǎn)左右孩子都存在:?獲取該結(jié)點(diǎn)的直接后繼結(jié)點(diǎn)
???//?該結(jié)點(diǎn)右子樹(shù)中最小的結(jié)點(diǎn)
???struct?Node*?temp?=?minValueNode(root->right);?

???//?將直接后繼結(jié)點(diǎn)的值拷貝給刪除結(jié)點(diǎn)
???root->key?=?temp->key;?

???//?刪除其直接后繼結(jié)點(diǎn)
???root->right?=?deleteNode(root->right,?temp->key);?
??}?
?}?

?//?如果樹(shù)中僅包含一個(gè)結(jié)點(diǎn)直接返回
?if?(root?==?NULL)?
??return?root;?

?//第二步:?更新當(dāng)前結(jié)點(diǎn)的深度
?root->height?=?1?+?max(height(root->left),?
??????height(root->right));?

?//?第三步:?獲取刪除結(jié)點(diǎn)的平衡因子
?//?判斷該結(jié)點(diǎn)是否平衡
?int?balance?=?getBalance(root);?

?//?如果結(jié)點(diǎn)為不平衡結(jié)點(diǎn)，分以下四種情況處理

?//?LL情況
?if?(balance?>?1?&&?getBalance(root->left)?>=?0)?
??return?rightRotate(root);?

?//?LR情況
?if?(balance?>?1?&&?getBalance(root->left)?0)?
?{?
??root->left?=?leftRotate(root->left);?
??return?rightRotate(root);?
?}?

?//?RR情況?
?if?(balance?-1?&&?getBalance(root->right)?<=?0)?
??return?leftRotate(root);?

?//?RL情況
?if?(balance?-1?&&?getBalance(root->right)?>?0)?
?{?
??root->right?=?rightRotate(root->right);?
??return?leftRotate(root);?
?}?

?return?root;?
}?

實(shí)戰(zhàn)應(yīng)用

題目描述

給定一個(gè)值 x ，返回一顆平衡二叉樹(shù)中比 x 大的結(jié)點(diǎn)個(gè)數(shù)

輸入輸出示例

輸入一個(gè)值 x ?= 10 和下面的一顆平衡二叉樹(shù)：

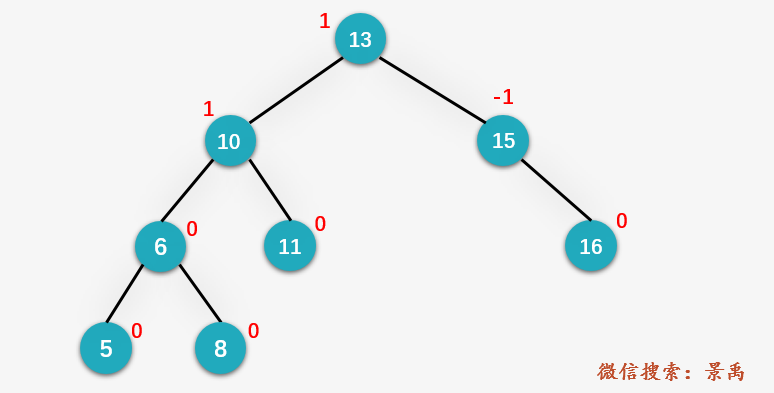
輸出：4

解釋：平衡二叉樹(shù)中比結(jié)點(diǎn)10大有 11，13，14，16 ，共4個(gè)結(jié)點(diǎn)。

題目解析

1. 對(duì)于平衡二叉樹(shù)中的每一個(gè)結(jié)點(diǎn)維護(hù)一個(gè) desc 字段，用于保存每一個(gè)結(jié)點(diǎn)所包含的子孫結(jié)點(diǎn)的個(gè)數(shù)。比如示例中結(jié)點(diǎn) 10 的 desc 的值就等于 4，結(jié)點(diǎn) 10 的子孫結(jié)點(diǎn)包含 6、11、5、8 四個(gè)結(jié)點(diǎn)。
2. 計(jì)算大于給定結(jié)點(diǎn)的節(jié)點(diǎn)數(shù)目就可以通過(guò)遍歷平衡二叉樹(shù)獲得了，具體包含以下三種情況：
• x 比當(dāng)前遍歷的結(jié)點(diǎn)的值大，我們則遍歷當(dāng)前結(jié)點(diǎn)的右孩子。
• x 比當(dāng)前遍歷的結(jié)點(diǎn)的值小，則大于指定結(jié)點(diǎn)的數(shù)目加上當(dāng)前結(jié)點(diǎn)右孩子的 desc 加上 2 （加 2 是因?yàn)楫?dāng)前結(jié)點(diǎn)以及當(dāng)前結(jié)點(diǎn)的右孩子都比指定的值 x 要大，當(dāng)然是當(dāng)前結(jié)點(diǎn)的右孩子存在的情況下）。具體操作是，判斷當(dāng)前結(jié)點(diǎn)的右孩子是否存在，如果存在則給大于 x 的結(jié)點(diǎn)數(shù)目加上當(dāng)前結(jié)點(diǎn)的右孩子的 desc 并加2，否則 給大于 x 的結(jié)點(diǎn)數(shù)目加 1 ；然后將當(dāng)前結(jié)點(diǎn)更新為其左孩子。
• 當(dāng) x 等于當(dāng)前結(jié)點(diǎn)的值，判斷 x 的右孩子是否存在，如果存在則將大于 x 的結(jié)點(diǎn)數(shù)目加上 x 的右孩子 desc ,然后再加上右孩子本身（即 1）；否則，右孩子不存在，則直接返回大于 x 的結(jié)點(diǎn)數(shù)目。

結(jié)點(diǎn)的定義中增加 desc 域：

struct?Node?{?
????int?key;?
????struct?Node*?left,?*right;?
????int?height;?
????int?desc;?
};?

我們以查找示例網(wǎng)絡(luò)中比結(jié)點(diǎn) 6 的結(jié)點(diǎn)數(shù)目為例講解，比結(jié)點(diǎn) 6 的結(jié)點(diǎn)數(shù)目用 count 表示且初始化為 0；

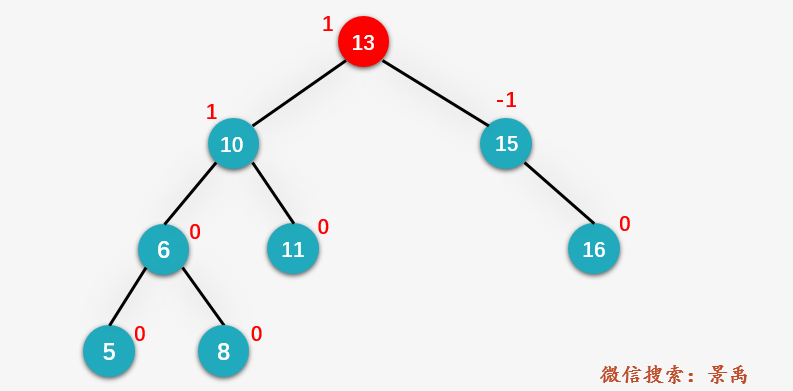
第一步：訪問(wèn)根結(jié)點(diǎn) 13 ，發(fā)現(xiàn)結(jié)點(diǎn) 6 的值比 13 小，則 count 的值加上 13 的右孩子 15 的 desc=1 ，再加上結(jié)點(diǎn) 13 和 15 本身， count = desc + 2 = 3 .

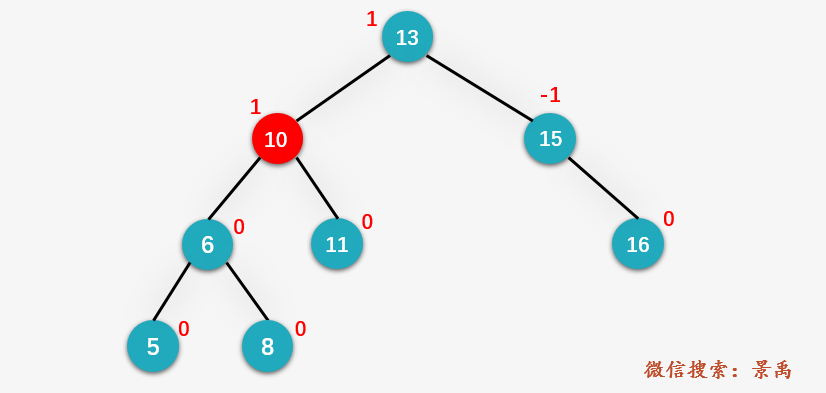
第二步：訪問(wèn)結(jié)點(diǎn) 13 的左孩子 10 ，6 < 10 ，則 count 的值應(yīng)加上 10 的右孩子 11 的 desc 的值，再加 2，其中結(jié)點(diǎn) 11 的 desc 的值為0，故 count = 3 + 2 = 5 .

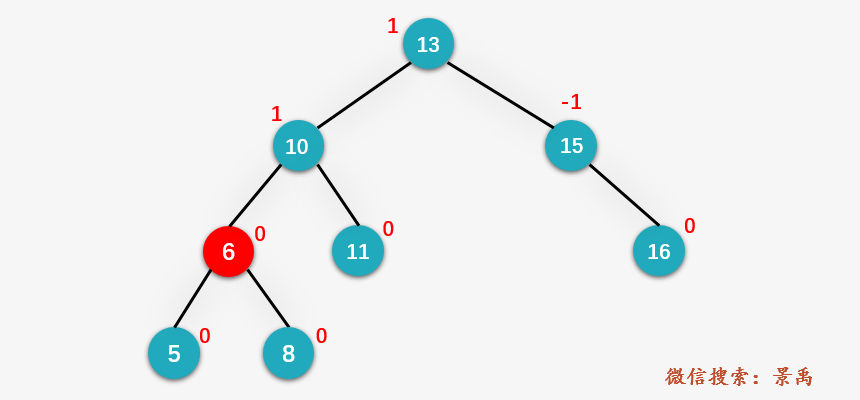
第三步：訪問(wèn)結(jié)點(diǎn) 10 的左孩子 6 ，發(fā)現(xiàn)與給定值相等，且結(jié)點(diǎn) 6 的右孩子存在，則 count 應(yīng)加上結(jié)點(diǎn) 6 的右孩子 8 的 desc 以及結(jié)點(diǎn) 8 本身，即 count = 5 + 1 = 6 .

其實(shí)歸結(jié)到最本質(zhì)，整個(gè)過(guò)程就是利用了二叉排序樹(shù)中，結(jié)點(diǎn)的右子樹(shù)的值大于結(jié)點(diǎn)，左子樹(shù)的值小于結(jié)點(diǎn)這樣的特性。

那么該如何計(jì)算每一個(gè)結(jié)點(diǎn)的 desc 域呢？

1. 插入：每當(dāng)插入一個(gè)新的結(jié)點(diǎn)，則給新插入結(jié)點(diǎn)的所有父結(jié)點(diǎn)的 desc 加 1 。當(dāng)然相應(yīng)的旋轉(zhuǎn)操作也需要進(jìn)行處理，稍后用圖進(jìn)行說(shuō)明。
2. 刪除操作：當(dāng)刪除一個(gè)結(jié)點(diǎn)，則將刪除結(jié)點(diǎn)的所有祖先結(jié)點(diǎn)的 desc 減 1 。同樣不論左旋還是右旋都需要進(jìn)行處理。

還是以之前的左旋和右旋圖說(shuō)明 desc 值的相應(yīng)變化：

左旋的情況下：

int?val?=?(T2?!=?NULL)???T2->desc?:?-1;?
x->desc?=?x->desc?-?(y->desc?+?1)?+?(val?+?1);?
y->desc?=?y->desc?-?(val?+?1)?+?(x->desc?+?1);?

當(dāng) 不為空時(shí)，用一個(gè)臨時(shí)變量 val 保存 的 desc 的值，否則將 val 賦值為 -1 。左旋操作后， x 的 desc 的值將等于其原來(lái)的值減去其原來(lái)的右孩子結(jié)點(diǎn) y 的 desc ，再加上左旋之后其右孩子 的 desc + 1 ，即 val + 1 。

右旋的情況下：

int?val?=?(T2?!=?NULL)???T2->desc?:?-1;?
y->desc?=?y->desc?-?(x->desc?+?1)?+?(val?+?1);?
x->desc?=?x->desc?-?(val?+?1)?+?(y->desc?+?1);?

與左旋類似，當(dāng) 不為空時(shí)，用一個(gè)臨時(shí)變量 val 保存 ?的 desc 的值，否則將 val 賦值為 -1 。右旋操作之后，y 的值變?yōu)槠渲暗?desc j減去 x 的 desc+1 ，再加上 的 desc + 1 ，即 val+1 。而 x 的 desc 則變?yōu)槠湓瓉?lái)的 desc 的值減去 val+1 ，然后再加上旋轉(zhuǎn)后的 y->desc + 1 。

有了上面的基礎(chǔ)，我們可以一起先來(lái)看一下這道題目的左旋和右旋操作。

左右旋操作代碼： 本質(zhì)上與之前講過(guò)的平衡二叉樹(shù)插入和刪除操作涉及的左旋與右旋一樣，只是增加了上面的 desc 域的處理操作 （需要復(fù)習(xí)的就再看一遍代碼，不需要的直接跳過(guò)）。

struct?Node*?rightRotate(struct?Node*?y)?
{?
?struct?Node*?x?=?y->left;?
?struct?Node*?T2?=?x->right;?

?//旋轉(zhuǎn)操作，對(duì)著圖看
?x->right?=?y;?
?y->left?=?T2;?

?//?高度更新
?y->height?=?max(height(y->left),?height(y->right))?+?1;?
?x->height?=?max(height(x->left),?height(x->right))?+?1;?

?//?更新desc?
?int?val?=?(T2?!=?NULL)???T2->desc?:?-1;?
?y->desc?=?y->desc?-?(x->desc?+?1)?+?(val?+?1);?
?x->desc?=?x->desc?-?(val?+?1)?+?(y->desc?+?1);?

?return?x;?
}?


struct?Node*?leftRotate(struct?Node*?x)?
{?
?struct?Node*?y?=?x->right;?
?struct?Node*?T2?=?y->left;?

?//左旋?
?y->left?=?x;?
?x->right?=?T2;?

?//更新高度
?x->height?=?max(height(x->left),?height(x->right))?+?1;?
?y->height?=?max(height(y->left),?height(y->right))?+?1;?

?//更新?desc?
?int?val?=?(T2?!=?NULL)???T2->desc?:?-1;?
?x->desc?=?x->desc?-?(y->desc?+?1)?+?(val?+?1);?
?y->desc?=?y->desc?-?(val?+?1)?+?(x->desc?+?1);?

?return?y;?
}?

獲取結(jié)點(diǎn) N 的平衡因子(復(fù)習(xí)）：

int?getBalance(struct?Node*?N)?
{?
?if?(N?==?NULL)?
??return?0;?
?return?height(N->left)?-?height(N->right);?
}?

平衡二叉樹(shù)結(jié)點(diǎn)的插入操作（增加了對(duì)desc的處理，其他和之前講的插入操作的實(shí)現(xiàn)一致）：

struct?Node*?insert(struct?Node*?node,?int?key)?
{?
?/*?標(biāo)準(zhǔn)的BST的插入操作?*/
?if?(node?==?NULL)?
??return?(newNode(key));?

?if?(key?key)?{?
??node->left?=?insert(node->left,?key);?
??node->desc++;?//插入結(jié)點(diǎn)的左右祖先結(jié)點(diǎn)的desc++
?}?

?else?if?(key?>?node->key)?{?
??node->right?=?insert(node->right,?key);?
??node->desc++;?
?}?

?else?//?二叉排序樹(shù)中不允許插入相同的值
??return?node;?

?/*?2.?更新祖先結(jié)點(diǎn)的高度?*/
?node->height?=?1?+?max(height(node->left),?
??????height(node->right));?

?/*?3.?獲取祖先結(jié)點(diǎn)的平衡因子，判斷是否平衡*/
?int?balance?=?getBalance(node);?

?//?結(jié)點(diǎn)不平衡，分一下四種情況處理

?//?LL
?if?(balance?>?1?&&?key?left->key)?
??return?rightRotate(node);?

?//?RR?
?if?(balance?-1?&&?key?>?node->right->key)?
??return?leftRotate(node);?

?//?LR
?if?(balance?>?1?&&?key?>?node->left->key)?{?
??node->left?=?leftRotate(node->left);?
??return?rightRotate(node);?
?}?

?//?RL
?if?(balance?-1?&&?key?right->key)?{?
??node->right?=?rightRotate(node->right);?
??return?leftRotate(node);?
?}?

?/*返回插入結(jié)點(diǎn)之后，樹(shù)的根結(jié)點(diǎn)*/
?return?node;?
}?

至于刪除操作的修改代碼，我就不在這里放了，需要的可以對(duì)上面的平衡二叉樹(shù)刪除操作的代碼修改一下即可。我們主要看一下統(tǒng)計(jì)大于給定值 x 的結(jié)點(diǎn)個(gè)數(shù)的代碼。

統(tǒng)計(jì)大于結(jié)點(diǎn) x 的結(jié)點(diǎn)數(shù)目

int?CountGreater(struct?Node*?root,?int?x)?
{?
?int?res?=?0;?

?//?查找結(jié)點(diǎn)?x，?同時(shí)更新?res的值
?while?(root?!=?NULL)?{?

??//保存當(dāng)前結(jié)點(diǎn)的右孩子的desc
??//不為空則保存root->right-desc
??//否則保存?-1
??int?desc?=?(root->right?!=?NULL)???
????root->right->desc?:?-1;?

??//如果root的值大于x,則說(shuō)明?x?位于左子樹(shù)當(dāng)中
??//res = res +?當(dāng)且結(jié)點(diǎn)右孩子的desc + 2
??if?(root->key?>?x)?{?
???res?=?res?+?desc?+?1?+?1;?
???root?=?root->left;?
??}?//當(dāng)root的值小于 x，則說(shuō)明 x 位于右子樹(shù)當(dāng)中，繼續(xù)查找
??else?if?(root->key????root?=?root->right;?
??}
??else?{?//當(dāng)相等時(shí)，res?=?res?+?x的右孩子的desc?+?1.
???res?=?res?+?desc?+?1;?
???break;?
??}?
?}?
?return?res;?
}?