我們真的搞懂這些排序算法了嗎？(二）

前面給大家介紹了冒泡排序和簡單選擇排序，沒看過的同學可以先看下這個文章我們真的搞懂這些排序算法了嗎？（一），今天咱們再來拆解兩個新的排序排序算法。

? ?直接插入排序（Straight Insertion Sort）

袁記菜館內(nèi)

袁廚：好嘞，我們打烊啦，一起來玩會撲克牌吧。

小二：好啊，掌柜的，咱們玩會斗地主吧。

相信大家應該都玩過撲克牌吧，我們平常摸牌時，是不是一邊摸牌，一邊理牌，摸到新牌時，會將其插到合適的位置。這其實就是我們的插入排序思想。

直接插入排序：將一個記錄插入到已經(jīng)排好序的有序表中，從而得到一個新的有序表。通俗理解，我們首先將序列分成兩個區(qū)間，有序區(qū)間和無序區(qū)間，我們每次在無序區(qū)間內(nèi)取一個值，在已排序區(qū)間中找到合適的插入位置將其插入，并保證已排序區(qū)間一直有序。下面我們看一下動圖吧。

注：為了更清晰表達算法思想，則采用了挖掉待排序元素的形式展示，后面也會采取此形式表達。

直接插入排序代碼

class?Solution?{
????public?int[]?sortArray(int[]?nums)?{
????????//注意?i?的初始值為?1，也就是第二個元素開始
????????for?(int?i?=?1;?i?????????????//待排序的值
????????????int?temp?=?nums[i];
????????????//需要注意
????????????int?j;
????????????for?(j?=?i-1;?j?>=?0;?--j)?{
????????????????//找到合適位置
????????????????if?(temp?????????????????????nums[j+1]?=?nums[j];
????????????????????continue;
????????????????}?
????????????????//跳出循環(huán)
????????????????break;
????????????}
????????????//插入到合適位置，這也就是我們沒有在?for?循環(huán)內(nèi)定義變量的原因
????????????nums[j+1]?=?temp;
????????}
????????return?nums;
????}
}

注：可以左右滑動

直接插入排序時間復雜度分析

最好情況時，也就是有序的時候，我們不需要移動元素，每次只需要比較一次即可找到插入位置，那么最好情況時的時間復雜度為O(n)。

最壞情況時，即待排序表是逆序的情況，則此時需要比較2+3+…+n = (n+2)(n-1)/2,移動次數(shù)也達到了最大值，3+4+5+….n+1 = (n+4)(n-1)/2,時間復雜度為O(n^2).

我們每次插入一個數(shù)據(jù)的時間復雜度為O(n)，那么循環(huán)執(zhí)行 n 次插入操作，平均時間復雜度為O(n^2)。

直接插入排序空間復雜度分析

根據(jù)動畫可知，插入排序不需要額外的存儲空間，所以其空間復雜度為O(1)

直接插入排序穩(wěn)定性分析

我們根據(jù)代碼可知，我們只會移動比 temp 值大的元素，所以我們排序后可以保證相同元素的相對位置不變。所以直接插入排序為穩(wěn)定性排序算法。

? ?希爾排序 (Shell's Sort)

我們在之前說過直接插入排序在記錄基本有序的時候和元素較少時效率是很高的，基本有序時，只需執(zhí)行少量的插入操作，就可以完成整個記錄的排序工作。當元素較少時，效率也很高，就比如我們經(jīng)常用的 Arrays.sort (),當元素個數(shù)少于47時，使用的排序算法就是直接插入排序。那么希爾排序和直接插入排序有什么關系呢？

希爾排序是插入排序的一種，又稱“縮小增量排序”（Diminishing Increment Sort），是直接插入排序的高級變形，其思想簡單點說就是有跨度的插入排序，這個跨度會逐漸變小，直到變?yōu)?1，變?yōu)?1 時記錄也就基本有序，這時用到的也就是我們之前講的直接插入排序了。

基本有序：就是小的關鍵字基本在前面，大的關鍵字基本在后面，不大不小的基本在中間。見下圖。

我們已經(jīng)了解了希爾排序的基本思想，下面我們通過一個繪圖來描述下其執(zhí)行步驟。

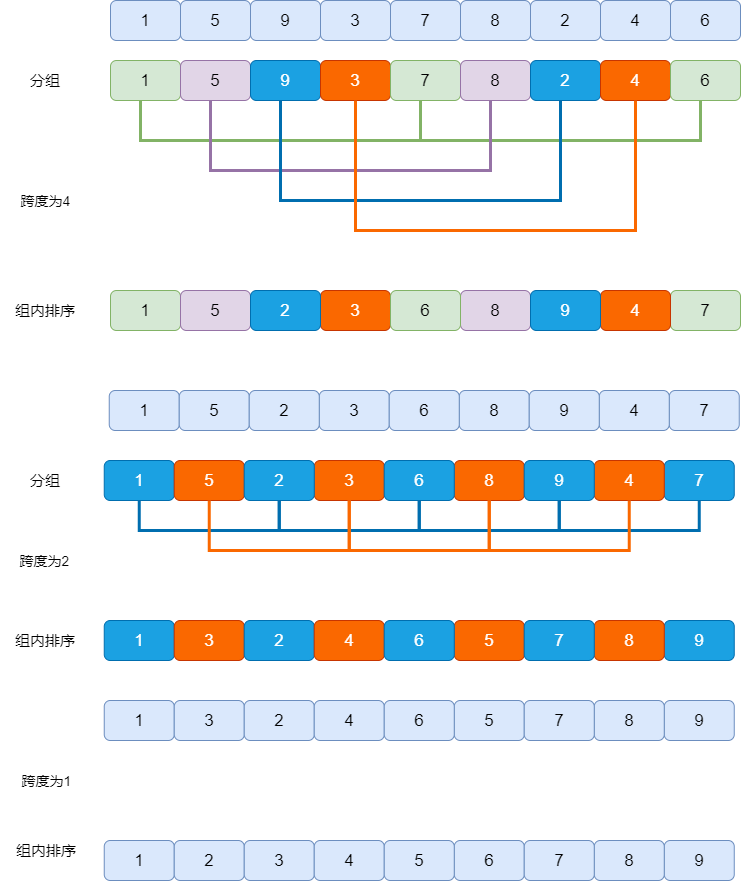
先逐步分組進行粗調(diào)，再進行直接插入排序的。這就是希爾排序。我們剛才的分組跨度（4，2，1）被稱為希爾排序的增量，我們上面用到的是逐步折半的增量方法，這也是在發(fā)明希爾排序時提出的一種樸素方法，被稱為希爾增量，

下面我們用視頻模擬下使用希爾增量的希爾排序的執(zhí)行過程

一定要看呀，嗷嗷解壓，有聲音滴

注：大家可以關注下我的視頻號呀，以后會在這里分享一些花里胡哨滴東西，關鍵是視頻號有評論，想夸我?guī)浀木蛠磉@里吧，哈哈。

大家可能看了視頻模擬，也不是特別容易寫出算法代碼，不過你們看到代碼肯定會很熟悉滴。

希爾排序代碼

注：同樣可以左右滑動

class?Solution?{
????public?int[]?sortArray(int[]?nums)?{
????????int?increment?=?nums.length;
????????//注意看結束條件
????????while?(increment?>?1)?{
????????????//這里可以自己設置
????????????increment?=?increment?/?2;
????????????//根據(jù)增量分組
????????????for?(int?i?=?0;?i?????????????????//這快是不是有點面熟，回去看看咱們的插入排序
????????????????for?(int?j?=?i?+?increment;?j?????????????????????int?temp?=?nums[j];
????????????????????int?k;
????????????????????for?(k?=?j?-?increment;?k?>=?0;?k?-=?increment)?{
????????????????????????if?(temp?????????????????????????????nums[k+increment]?=?nums[k];
????????????????????????????continue;
????????????????????????}
????????????????????????break;
????????????????????}
????????????????????nums[k+increment]?=?temp;
????????????????}
????????????}
????????}
????????return?nums;
????}
}

我們剛才說，我們的增量可以自己設置的，我們上面的例子是用的希爾增量，下面我們看這個例子，看看使用希爾增量會出現(xiàn)什么問題。

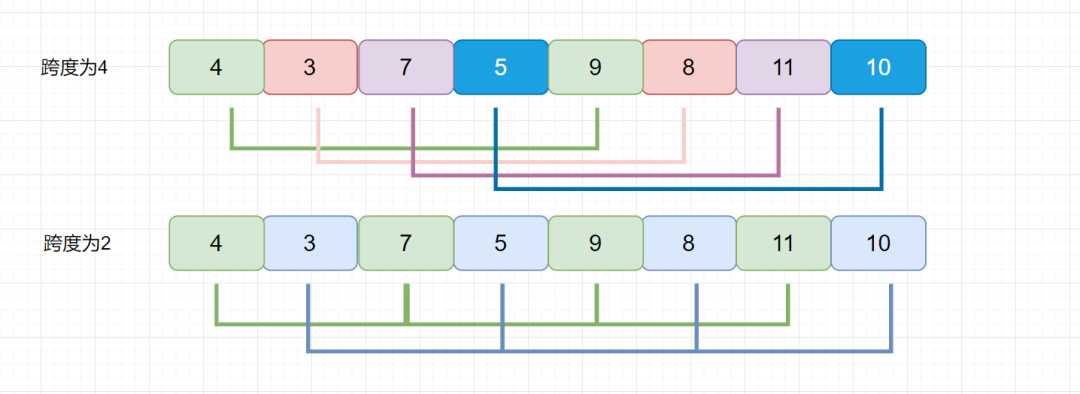
我們發(fā)現(xiàn)無論是以 4 為增量，還是以 2 為增量，每組內(nèi)部的元素沒有任何交換。直到增量為 1 時，數(shù)組才會按照直接插入排序進行調(diào)整。所以這種情況希爾排序的效率是低于直接插入排序呢？

我們的希爾增量因為每一輪之間是等比的，所以會有盲區(qū)，這里增量的選取就非常關鍵了。

下面給大家介紹兩個比較有代表性的 Sedgewick 增量和 Hibbard 增量

Hibbard增量序列如下：

1，3，7，15……

通項公式2 ^ k-1

利用此種增量方式的希爾排序，最壞時間復雜度為O(n^(3/2))

上面是兩種比較具有代表性的增量方式，可究竟應該選取怎樣的增量才是最好，目前還是一個數(shù)學難題。不過我們需要注意的一點，就是增量序列的最后一個增量值必須等于1才行。

希爾排序時間復雜度分析

希爾排序的時間復雜度跟增量序列的選擇有關，范圍為 O(n^(1.3-2)) 在此之前的排序算法時間復雜度基本都是O(n^2),希爾排序是突破這個時間復雜度的第一批算法之一。

希爾排序空間復雜度分析

根據(jù)我們的視頻可知希爾排序的空間復雜度為 O(1),

希爾排序的穩(wěn)定性分析

我們見下圖，一起來分析下希爾排序的穩(wěn)定性。

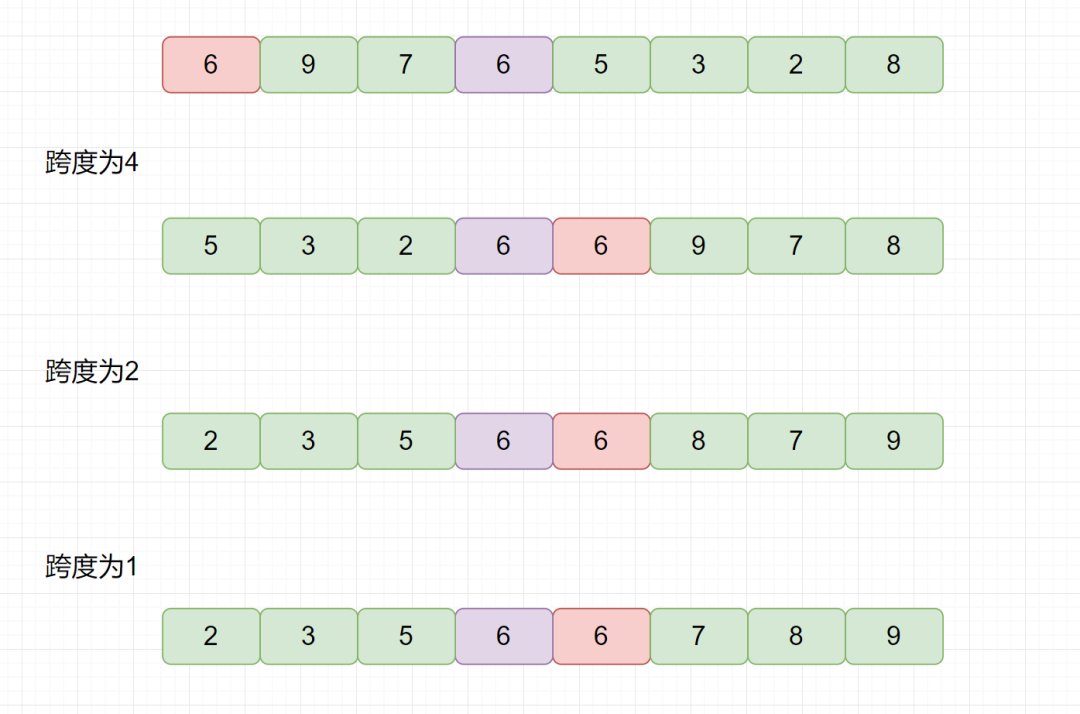
通過上圖，可知，如果我們選用 4 為跨度的話，交換后，兩個相同元素 2 的相對位置會發(fā)生改變，所以希爾排序是一個不穩(wěn)定的排序