中科院 AI 團隊最新研究發(fā)現(xiàn)，大模型可通過自我驗證提高推理性能

推理能力是機器接近人類智能的一個重要指標。

最近的大型語言模型（Large language mode，LLM）正在變得越來越擅長推理，背后的一個關鍵技術是思維鏈（chain-of-thought，CoT），簡單來說，CoT 可以讓 LLM 模擬人類思考的過程，幫助大型語言模型生成一個推理路徑，將復雜的推理問題分解為多個簡單的步驟，而不僅僅只是一個最終答案，從而增強模型的推理能力。

對人類而言，我們推斷得出一個結論后，往往會通過重新驗證來進行核對、避免錯誤。但當 LLM 在通過 CoT 執(zhí)行復雜推理尤其是算術和邏輯推理的過程中若出現(xiàn)錯誤，會在一定程度上影響推理效果，所以不得不進行人工驗證。

那么能不能讓語言模型也具備自我糾錯和自我驗證的能力呢？

近日，中國科學院自動化所的研究團隊提出了一種新方法證明了 LLM 可對自己的推理結論進行可解釋的自我驗證，從而大大提高推理性能，這讓 LLM 朝著人類智能又前進了一步。

論文地址：https://arxiv.org/pdf/2212.09561.pdf

1 正向推理+反向驗證

當涉及復雜推理時，語言模型往往缺乏穩(wěn)健性，一旦發(fā)生任何一個小錯誤，都可能會改變命題的全部含義，從而導致出現(xiàn)錯誤答案。使用CoT 提示進行推理時，問題會更嚴重，由于模型沒有糾錯機制，以至于很難從錯誤的假設中糾正過來。

以往的一種解決方法是通過訓練驗證器（verififiers）來評估模型輸出正確性。但訓練驗證器有三個大缺點：需要大量的人力和計算資源、可能存在誤報、可解釋性差。

為此，中科院團隊提出讓 LLM 進行自我驗證。

首先，假設推理問題中的所有條件對于得出結論都是必要的，給定結論和其他條件后，可推導出其余條件。自我驗證分兩個階段進行：

• 正向推理，LLM 生成候選思維鏈和結論給定的問題文本；

• 反向驗證，使用 LLM 來驗證條件是否滿足候選結論，并根據(jù)驗證分數(shù)對候選結論進行排序。

如下圖，對于“Jackie 有 10 個蘋果（f1），Adam 有 8 個蘋果（f2），Jackie 比 Adam 多了多少個蘋果？”這個問題，可從 f1 和 f2 推理出結論 fy。然后，通過反向驗證來檢驗該結論的準確性，就像解方程一樣，如果以 f2 和 fy 為條件，可以得出 f1，通過驗證 f1 是否與原來的 f1 結果一致，可以判斷 fy 的正確性。

圖 1：正向推理與反向驗證

研究表明，LLM 僅需少量提示即可使用自我驗證，無需訓練或梯度更新。它們用候選結論來驗證，解決了原 CoT 中偏離正確思維過程的問題。而且，驗證分數(shù)源自整個思維推理過程，可解釋性很高。

通過對 GPT?3、CODEX 和 Instruct?GPT 等大模型的實驗分析，這項研究證明了 LLM 具備可解釋的自我驗證能力。

2 LLM 的自我驗證過程

自我驗證的整個過程如圖 2所示。第一步與 CoT 類似，但研究通過采樣解碼生成多個候選結論，計算每個候選結論的驗證分數(shù)，并選擇最高分數(shù)作為最終結論。

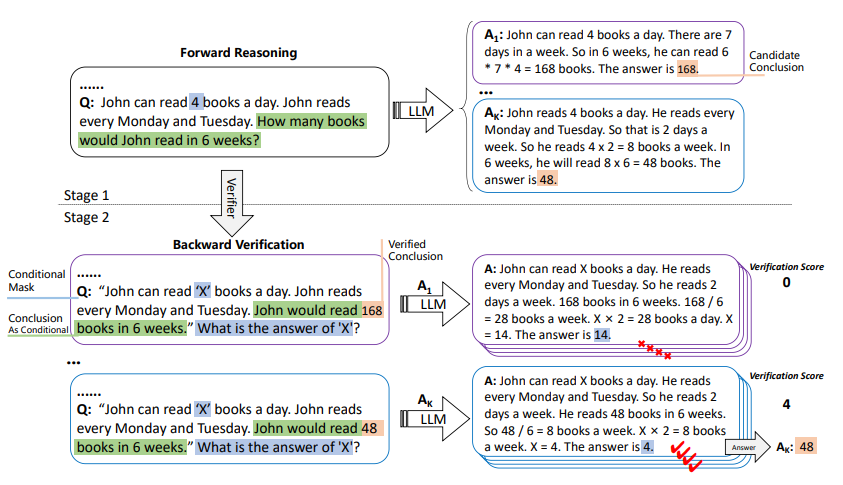
圖 2：自我驗證示例；LLM 在第一階段中生成一些候選結論，三個預訓練語言模型用于大量自動構建的數(shù)值推理問題，但這些方法需要大量的數(shù)據(jù)和專家注釋，然后 LLM 依次驗證這些結論，統(tǒng)計推理正確的屏蔽條件的個數(shù)作為第二階段的驗證分數(shù)

圖 3：這是一個需要使用多個條件的示例；如果只屏蔽第一個證據(jù)，則不需要這個證據(jù)（前向推理時，需要計算周末的錢，周五的工作時數(shù)不影響最終結論）。因此，我們無法根據(jù)現(xiàn)有條件和任何候選結論來預測此證據(jù)

2.1 候選結論生成

給定一個語言模型 M 和一個問答數(shù)據(jù)集 D，CoT 為 D 設計了一組樣本 C，其中包含 n 個樣本，epoch 樣本有包含條件和問題的輸入 X，思維過程 t 和結論 y。這些示例用作測試時間的輸入。通常 n 是一位數(shù)，因此需要語言模型 M 在生成 y 之前安裝 C 生成 t 的提示：C 中的每個示例都連接為提示。

使用 Sampling 解碼生成 K  y，K 是 y 的個數(shù)。具體來說，采樣譯碼是一種隨機譯碼方法，它可以在每一步從可能生成的詞的概率分布中采樣來選擇下一個詞，重復使用 Sampling 解碼可以得到多個候選結論。

2.2 條件和結論的重寫

對輸入的 X 進一步細分為其中每個 f 是一個條件，q 是一個問題。我們使用命令“請把問題和答案改成完整的陳述句[q] The answer is [y]”通過 M 把 q 和 y 改成新的陳述句 fy 。

在問題生成上，問題的多樣性使得在實際操作中很難平衡問題和答案之間的連貫性和事實一致性的需要，因此直接屏蔽條件。首先，通過正則匹配找到 f1 中的值改寫為 X，在新問題的末尾加入“What is the answer of X？” ，從而提示語言模型指示目標。

2.3 依次驗證

如圖 4 所示，如果給定的 X 不滿足所有條件都是結論的必要條件，可以發(fā)現(xiàn)只有掩碼的第一個條件會有局限性，難以準確評估其驗證分數(shù)。為了解決這個問題，可以采用多個條件依次驗證的方法：依次用 X 替換原始 X 中出現(xiàn)的所有 f，并要求 M 重新預測它，提高驗證的可靠性和準確性。

圖 4：在八個基準數(shù)據(jù)集上進行評估，這些基準數(shù)據(jù)集涵蓋了算術推理、常識推理和邏輯推理任務

2.4 驗證分數(shù)

研究人員設計了一個類似于正向推理的 CoT 以指導 LLM 生成解決過程。而反向驗證過程類似于求解方程式，可將其最終結果與屏蔽條件進行匹配。

由于 LLM 本身性能有限，在反向驗證過程中，單次解碼會因隨機性導致驗證結果出現(xiàn)偏差，難以保證更準確的驗證分數(shù)。為了解決這個問題，采樣解碼過程將重復 P 次，這樣驗證分數(shù)就可以更準確地反映模型對給定結論的置信度。

驗證分數(shù)計算如下：

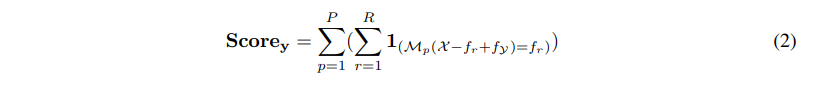
其中，1（.）為指示函數(shù)，從生成的 K 個候選答案中選擇驗證分數(shù)最高的一個作為結果，

3 LLM 的自我驗證能增強推理性能

任務和數(shù)據(jù)集

此項研究評估了6個算術推理數(shù)據(jù)集，進一步證明了自我驗證在常識推理和邏輯推理數(shù)據(jù)集上的有效性。這些數(shù)據(jù)集在輸入格式方面高度異質：

• 算術，前兩個是一步推理的數(shù)據(jù)集，后四個需要多步推理，解決起來比較有挑戰(zhàn)性

• 常識，CommonsenseQA（CSQA）需要使用常識和關于世界的知識才能準確回答具有復雜含義的問題，其依賴于先驗知識來提供準確的響應

• 邏輯，日期理解要求模型從一個上下文推斷日期

型號

研究人員在實驗中測試來原始 CODEX 模型和 Instruct?GPT 模型，此外還通過使用 GPT?3 進行分析實驗，研究了不同參數(shù)級別對可驗證性的影響，LLM  的大小范圍為 0.3B 到 175B 。這些實驗使用了 OpenAI 的 API 來獲得推理結果。

實驗結果表明，使用了自我驗證的兩個模型在多個任務中實現(xiàn)了 SOTA 性能。

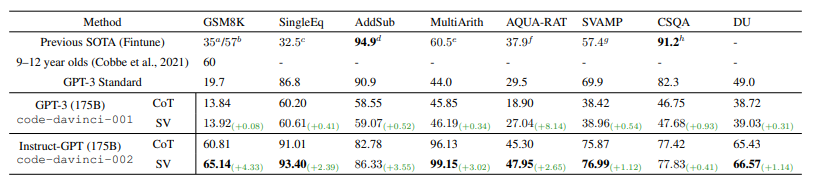
圖 5：推理數(shù)據(jù)集上的問題解決率（%）

可以看到，自我驗證在算術數(shù)據(jù)集上實現(xiàn)了1.67%/2.84%的平均改進，并為常識推理和邏輯推理任務帶來了少量優(yōu)化。此外，自我驗證還直接導致高性能 Instruct?GPT 模型結果平均增加2.33%，這表明，具有強大前向推理能力的模型也具有很高的自我驗證能力。

研究人員進一步發(fā)現(xiàn)了以下幾個關鍵結論。

可用條件越多，驗證準確性越高

圖 6：單條件驗證與多條件驗證的問題解決率（%）比較

圖 6 中觀察了對六個不同算術數(shù)據(jù)集使用單一條件掩碼的效果：由于這些數(shù)據(jù)集輸入中的每個數(shù)字都可以被視為一個條件，因此可以研究增加驗證條件數(shù)量的影響。經(jīng)大多數(shù)實驗可發(fā)現(xiàn)，多條件掩碼比單條件掩碼表現(xiàn)更好，并且都比原始 CoT 表現(xiàn)更好。

模型越大，自我驗證能力越強

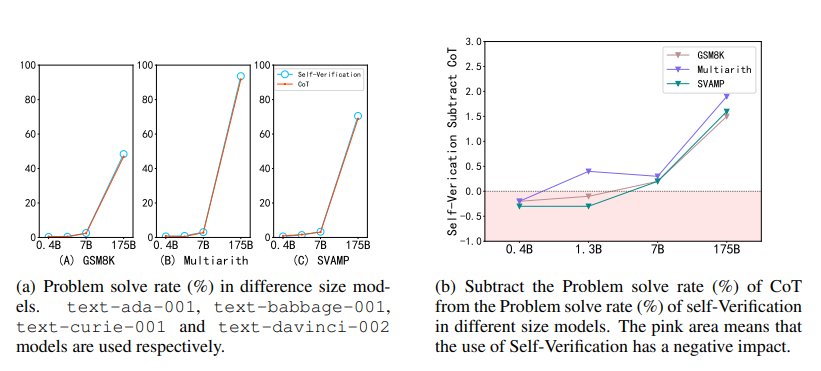
圖 7：不同尺寸模型的自我驗證能力

圖 7顯示了參數(shù)從 0.4B 到 175B 的 GPT?3 模型能力。實驗結果表明，當參數(shù)較小時，模型的自驗證能力較弱，甚至不如 CoT 的原始性能。這說明，模型的自我驗證也是一種涌現(xiàn)能力，且往往出現(xiàn)在更大的模型中。

思維鏈提示很少并不影響自我驗證能力

圖 8：2 次提示和8 次提示的問題解決率（%）比較

圖 8 所示的實驗結果顯示了不同的提示量對性能的影響。可以看到，自我驗證在較小的樣本中表現(xiàn)出更大的穩(wěn)健性，甚至低至 2 次，這時候其 8 次提示的性能是 99.6%，而 CoT 只有 98.7%。不僅如此，即使只有 4 個提示（2 個 CoT 提示+ 2 個自我驗證提示），自我驗證也明顯優(yōu)于 CoT 8 次提示，突出了自我驗證在數(shù)據(jù)有限情況下的重要性。

圖 9：不同驗證方式的提示對比

與其它方法相比，條件掩碼的自我驗證性能更優(yōu)

有另一種方法可以驗證模型答案的正確性：真-假項目驗證，這以方法是模型對所有條件進行二分判斷，如圖 12 所示，不覆蓋任何條件。此研究還提供了一個反向推理的例子，并嘗試讓模型自動從結論是否滿足條件進行反向推理，但實驗結果如圖 10 所示，真-假項目驗證的性能，要落后于條件掩碼驗證的性能。

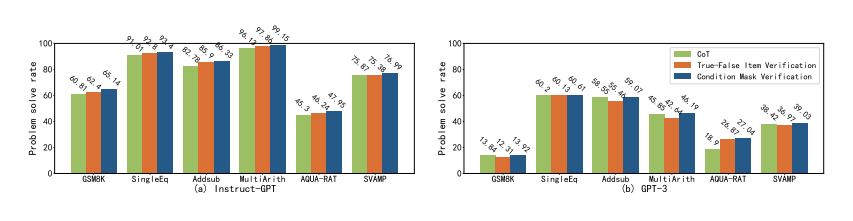
圖 10：6 個算術數(shù)據(jù)集的問題解決率（%）條件掩碼驗證和真-假項目驗證的比較

為了理解這種差距的原因，研究分析了具體案例，如圖 11 所示，結果表明：（1）缺乏明確的反向推理目標導致模型再次從正向推理，該結果沒有意義、并且不利用現(xiàn)有的結論；（2）真-假項目驗證提供了所有的條件，但這些條件可能會誤導模型的推理過程，使模型沒有起點。因此，更有效的做法是使用條件掩碼驗證，從而更好地激發(fā)模型的自我驗證能力。

圖 11：一些實際生成案例進一步展示了不同驗證方法的影響

LLM 的自我驗證能糾錯，但可也能「誤傷」

圖 12 展示了 LLM 使用自我驗證來驗證其自身結果的詳細結果：

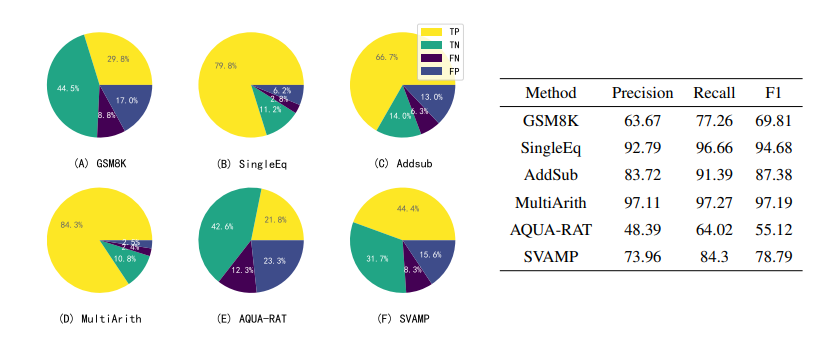
圖 12：使用 Instruct?GPT 為八個數(shù)據(jù)集中的每一個生成了五組候選答案，然后利用 Instruct?GPT 的自我驗證 能力，對它們進行一一判斷和排序

左邊的扇形圖顯示了自我驗證產(chǎn)生的候選結論的預測結果。LLM 在每次提示中產(chǎn)生1-5個候選結論（由于 LLM 的自洽性，可能會產(chǎn)生相同的候選結論），這些結論可能是正確的，也可能是錯誤的，再通過 LLM 自我驗證來檢驗這些結論，并將其類為真陽性（TP）、真陰性（TN）、假陰性（FN）或假陽性（FP）。可以發(fā)現(xiàn)，除了 TP 和 TN 之外，還有大量的 FN，但只有少量的 FP。

右邊的表格顯示了召回率明顯高于準確率，由此可以說明，LLM 的自我驗證可以準確剔除不正確的結論，但也可能將一個正確結論錯誤地認為是不正確的。這可能是由于反向驗證時方程錯誤或計算錯誤造成的，這一問題將在未來解決。

最后總結一下，這項工作提出的自我驗證方法能夠讓大型語言模型和提示來引導模型驗證自己的結果，能提高 LLM 在推理任務中的準確性和可靠性。

但需要注意的是，這些提示是人為構造的，可能會引入偏差。所以方法的有效性會受到 LLM 產(chǎn)生的候選結論中正確答案的存在的限制，因此取決于模型正確前向推理的能力。

此外，該方法涉及生成多個候選 CoT 和結論，這對于 LLM 來說也存在計算資源的消耗。雖然它可以幫助 LLM 避免來自不正確的 CoT 干擾，但也可能無法完全消除推理過程中的錯誤。

編輯：王菁

校對：林亦霖