KMP模式匹配算法-串的應(yīng)用
前言
好久不見(jiàn)~各位看客老爺們,距離上次小向上班已經(jīng)過(guò)去了好久--TT,小向也不想,但是被一個(gè)地方卡住了好久,最近才弄清楚。那么廢話不多說(shuō),讓我們進(jìn)入今天的主題叭~數(shù)據(jù)結(jié)構(gòu)之串及其應(yīng)用KMP模式匹配算法。還記得前段時(shí)間,小編參加英語(yǔ)考試,面對(duì)大量的生詞,小編人都嚇傻了,可是全部記憶一遍肯定來(lái)不及,記憶出現(xiàn)頻率最高的肯定是效率最快的,這件事情說(shuō)起來(lái)很簡(jiǎn)單,但是怎么才能知道什么單詞出現(xiàn)的頻率最高呢?這里面涉及到許許多多的東西,今天我們就不全部展開(kāi)講解,不過(guò),這里面最重要的其實(shí)就是去找一個(gè)單詞在一篇文章中的定位問(wèn)題。即串的模式匹配。

什么是串?
下面讓我們來(lái)了解一下串。
雖然看到串的第一眼,大家可能有一點(diǎn)蒙的感覺(jué),串?羊肉串?或者是別的balabala的東西。其實(shí)這里的串,指的是字符串。串:由零個(gè)或者多個(gè)字符組成的有限序列,又名叫字符串。一般我們把串記為s=”a1a2a3……an”,其中s是串的名稱(chēng),用雙引號(hào)或者單引號(hào)括起來(lái)的內(nèi)容就是串的值,注意,在這個(gè)位置,雙引號(hào)不是串的內(nèi)容。打個(gè)比方說(shuō),《靜夜思》“床前明月光,疑是地上霜。舉頭望明月,低頭思故鄉(xiāng)”,那么此時(shí),《靜夜思》就是串的名稱(chēng),“床前明月光……”才是內(nèi)容。
 零個(gè)字符是什么意思呢?就是啥也沒(méi)有,這樣的串,我們又稱(chēng)為空串,""直接這樣表示就可以了。他的長(zhǎng)度為0.在串的定義中我們可以發(fā)現(xiàn),串是有順序的,相鄰的字符之間有前驅(qū)和后繼的關(guān)系。并且串是有限的,一定要注意,串是有限的!
零個(gè)字符是什么意思呢?就是啥也沒(méi)有,這樣的串,我們又稱(chēng)為空串,""直接這樣表示就可以了。他的長(zhǎng)度為0.在串的定義中我們可以發(fā)現(xiàn),串是有順序的,相鄰的字符之間有前驅(qū)和后繼的關(guān)系。并且串是有限的,一定要注意,串是有限的!下面再讓我們認(rèn)識(shí)一個(gè)概念,主串,子串以及空格串。主串子串,其實(shí)很好理解,整個(gè)串的所有內(nèi)容就是主串,而串中任意個(gè)數(shù)的連續(xù)字符組成的子序列稱(chēng)為該串的子串。那空格串就更好理解了,就是只包含有限個(gè)空格的串,記住是有限個(gè)空格,可以不是一個(gè),但是不可能是無(wú)限個(gè)。現(xiàn)在再來(lái)看《靜夜思》,我們就知道了,整首古詩(shī)就是一個(gè)主串,而里面的每個(gè)句子或者每連續(xù)的幾個(gè)字,就是它的子串。
? 大致清楚了串的一些定義之后,我們來(lái)了解一下串的比較大小方式。對(duì)于兩個(gè)數(shù)來(lái)說(shuō),比較大小非常容易,2>1……。但是串怎么比較大小呢?其實(shí)串的比較大小方式大家猜應(yīng)該也都可以猜出來(lái),就是判斷他們挨個(gè)字母的前后順序。打一個(gè)比方來(lái)說(shuō),smart,stupid,他們的第一個(gè)字母都是s,認(rèn)為不存在大小差異,而第二個(gè)字母,”m”字母在”t”字母之前,所以”m”<”t”.
但是事實(shí)上,對(duì)于計(jì)算機(jī)來(lái)說(shuō),他是不知道哪個(gè)字母在前哪個(gè)字母在后的,他是通過(guò)組成串的字符之間的編碼來(lái)進(jìn)行的。現(xiàn)代計(jì)算機(jī)一般都是通過(guò)ASCII編碼,但是由于ASCII碼是用7位二進(jìn)制表示一個(gè)字符,總共只能表示128個(gè)字符,所以擴(kuò)展ASCII碼由8位二進(jìn)制數(shù)表示一個(gè)字符,這樣就可以表示256個(gè)字符,滿足了大部分國(guó)家的需要。可是,對(duì)于我們國(guó)家那可是遠(yuǎn)遠(yuǎn)不夠的,我們國(guó)家除了漢語(yǔ),還有土家語(yǔ),蒙古語(yǔ)……等等語(yǔ)言,所以就有了現(xiàn)在的Unicode編碼,一般用16位的二進(jìn)制數(shù)表示一個(gè)字符。
? ?那么現(xiàn)在我們就來(lái)正式的總結(jié)一下串的比較。
對(duì)于兩個(gè)長(zhǎng)度相等的串來(lái)說(shuō),必須每個(gè)相應(yīng)位置的字符都相等,才算是相等。即a1=b1,a2=b2,……,an=bn.
? 對(duì)于兩個(gè)長(zhǎng)度不相等的串來(lái)說(shuō),s1=”a1a2……an”,s2=”b1b2……bm”,
? 如果n
? 對(duì)于n
? 大致的了解了串以后,本來(lái)是應(yīng)該繼續(xù)介紹串的抽象數(shù)據(jù)類(lèi)型和儲(chǔ)存結(jié)構(gòu),但是串的抽象數(shù)據(jù)類(lèi)型和儲(chǔ)存結(jié)構(gòu)和棧類(lèi)似,這里就不多加敘述了。下面就讓我們進(jìn)入串的應(yīng)用部分,模式匹配算法。
樸素匹配算法
在剛開(kāi)始的時(shí)候,我覺(jué)得寫(xiě)一個(gè)查找單詞的程序很簡(jiǎn)單,就依次來(lái)比較就行了。過(guò)程在這里給大家進(jìn)行簡(jiǎn)單的介紹。
? 對(duì)于一個(gè)主串s=“annyainy”,我們需要查找子串t=””yibeizi”.我最開(kāi)始的思路是依次進(jìn)行匹配。
? 主串s從第一位開(kāi)始,s和t第一個(gè)字母不匹配,那么將s2和t1進(jìn)行比較,依次類(lèi)推,直到最后匹配成功。簡(jiǎn)單的說(shuō),就是對(duì)主串的每一個(gè)字符作為子串開(kāi)頭,與待匹配的字符串進(jìn)行匹配。對(duì)主串做大循環(huán),每個(gè)字符開(kāi)頭做T的長(zhǎng)度的小循環(huán),直到匹配成功或全部遍歷完成為止。
? 下面給出相應(yīng)的代碼
那么現(xiàn)在一個(gè)簡(jiǎn)單的匹配代碼我們已經(jīng)寫(xiě)出來(lái)了,但是這是最簡(jiǎn)單的,也是最慢的。現(xiàn)在讓我們來(lái)分析一下,如果每一次不成功的匹配都發(fā)生在串t的最后一個(gè)字符。舉一個(gè)例子,s為“aaaaaaaaaaaab”,t為“aaaaaaab”,那么需要每次匹配到最后我們才知道,原來(lái)不匹配。這樣的情況下,時(shí)間復(fù)雜度就是O((n-m+1)*m)。int index(string s, string t,int pos){int i = pos;/ pos是指開(kāi)始搜索的位置,即開(kāi)始搜索時(shí)的下標(biāo)int j = 0;/ 這是當(dāng)前子串的下標(biāo)while(i < s.length() && t < b.length()) / 只有當(dāng)i小于等于主串長(zhǎng)度且j小于等于子串長(zhǎng)度時(shí)進(jìn)行循環(huán){if(s[i] == t[j]){++i;++t;} else{i = i - j + 2 / i退回到上次匹配位置的下一位j = 1;}if(j = b.length())return i - b.length(); elsereturn 0;}
? 相信大家看到這樣分析下來(lái)肯定會(huì)說(shuō),這確實(shí)太麻煩了,甚至難以忍受,那么就讓我們來(lái)看看一種更高效的算法。由D.E.Knuth,J.H.Morris和V.R.Pratt發(fā)表的一個(gè)模式匹配算法,簡(jiǎn)稱(chēng)KMP算法。
KMP模式匹配算法
在最開(kāi)始,我們先來(lái)看一個(gè)串,s=abcababcaaccda……,t=abcabz,他們?cè)谶M(jìn)行匹配的時(shí)候,匹配到第六位時(shí)發(fā)現(xiàn)不匹配,按照樸素匹配算法,他們會(huì)依次往前移動(dòng)一位,再重新進(jìn)行比較,即整個(gè)匹配過(guò)程我們是通過(guò)s的i的值的不斷回溯來(lái)進(jìn)行,但是,我們知道,t的第一位和s的第一位肯定不匹配,依次類(lèi)推,直到和s的4位開(kāi)始比較,才算步入正軌,那么我們可不可以把這些很顯然不對(duì)的步驟刪掉,把那些肯定匹配的步驟跳過(guò)呢?對(duì),基于這種觀點(diǎn),大佬們提出了KMP算法來(lái)解決這些完全沒(méi)有必要的回溯。
? 如果i的值不回溯,也就是大小不能發(fā)生變化,那么要考慮的變化就是j的值了。通過(guò)對(duì)樸素匹配算法的觀察,我們可以發(fā)現(xiàn),要確定j值的變化,其實(shí)我們只要將當(dāng)前j所在的位置和前面進(jìn)行比較,如果出現(xiàn)了相同的字符,那么j的變化也會(huì)不一樣,也就是說(shuō),j值的變化只取決于自身而不取決于主串。
? 再拿上面的例子來(lái)說(shuō),t=abcdef,當(dāng)中沒(méi)有任何重復(fù)的字符,那么j就從6變?yōu)?,如果t=abcabz,當(dāng)匹配到z的時(shí)候,發(fā)現(xiàn)不匹配,此時(shí)j就從6變?yōu)?,而不是1,因?yàn)榍熬Y”ab”和z之前的后綴”ab”是相等的。由此我們就可以知道j的值取決于當(dāng)前字符之前的串的前后綴的相似度。
如果把t串的各個(gè)位置的j值變化定義為一個(gè)數(shù)組next,那么數(shù)組next的長(zhǎng)度就是t串的長(zhǎng)度,于是我們就可以得到下面的函數(shù)定義。
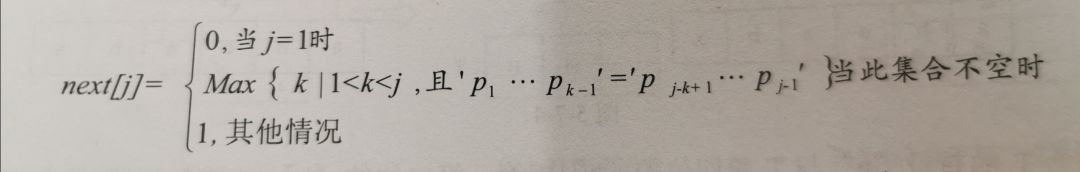
這里我們需要先明確一個(gè)概念,前綴和后綴。對(duì)于子串a(chǎn)cesdz來(lái)說(shuō),當(dāng)j=5時(shí),他的去掉第五個(gè)字符的子串是“aces”,前綴就是去掉再最后一個(gè)字符“s”,依次的子串,即a,ac,ace,那么后綴也很清楚了,去掉最前面一個(gè),即s,es,ces.
? 那么next數(shù)組是怎么推導(dǎo)的呢?對(duì)于子串a(chǎn)cesdz
1)當(dāng)j=1時(shí),next[1]=0.
2)當(dāng)j=2時(shí),j由1到j(luò)-1就只有字符“a”,屬于其他情況next[2]=1.
3)當(dāng)j=3時(shí),j由1到j(luò)-1的串就是“ac”,顯然“a”和”c”不等,屬于其他情況,next[3]=1.
4)以此類(lèi)推,最終next[j]為011111.
對(duì)于子串a(chǎn)ecaex
1)當(dāng)j=1時(shí),next[1]=0.
2)當(dāng)j=2時(shí),next[2]=1.
3)當(dāng)j=3時(shí),next[3]=1.
4)當(dāng)j=4時(shí),next[4]=1.
5)當(dāng)j=5時(shí),next[5]=2.
6)當(dāng)j=6時(shí),next[6]=3.
? ? ?我們根據(jù)經(jīng)驗(yàn)就可以知道,如果前后綴一個(gè)字符相等,那么next[j]=1+1,n個(gè)字符相等就是next[j]=1+n.
? ? ?下面我們給出next數(shù)值推導(dǎo)的代碼,
void get_next(string t, int* next){int i = 1;int j = 0;next[1] = 0;while(i < t[0])/*在這個(gè)位置t[0]表示t的長(zhǎng)度*/{if(j == 0 || t[i] == t[j]){++i;++j;next[i] = j;}elsej = next[j];}}
? ? 下面給出具體的匹配過(guò)程的代碼
/*此處s為主串,t為子串,pos為剛開(kāi)始匹配的位置*/int kmp(string s, string t, int pos){int i = pos;int j = 1;int next[255];get_next(t, next);while(i <= s[0] && j <= t[0]){if(j == 0 || s[i] == t[j]){++i;++j;} else{j = next[j];}}if(j > t[0])return i - t[0];elsereturn 0;}
? ? ?KMP算法的時(shí)間復(fù)雜度是O(n+m),相比較樸素匹配算法來(lái)說(shuō)是快了很多,但是這種優(yōu)勢(shì)只體現(xiàn)在重復(fù)部分很多的情況,否則差異不明顯。下面讓我們來(lái)看看KMP算法的進(jìn)一步優(yōu)化。
KMP的改良
?如果主串為s=aaaacde,子串為t=aaaaaz,next[j]=012345,i=5,j=5時(shí),發(fā)現(xiàn)不匹配,此時(shí)j變?yōu)?,仍然不匹配,然后變成3,依然不匹配,后面肯定也是一樣的不匹配,因?yàn)槎际莂,那么其實(shí)這些匹配都是不必要的,可以省去。那么我們完全可以用第一位的a的next數(shù)值來(lái)代替后面a的next數(shù)值,因此我們對(duì)next進(jìn)行了改良。
void get_naxtval(string t, int* nextval){int i = 1;int j = 0;nextval[1] = 0;while (i < t[0]){if (j == 0 || t[i] == t[j]){++i;++j;if (t[i] != t[j])nextval[i] = j; elsenextval[i] = nextval[j];}}}
? 匹配算法和之前的是一樣的這里就不再重復(fù)。這里nextval的推導(dǎo)就也不重復(fù)了,和next的推導(dǎo)過(guò)程大致相同。
KMP的再改良
? ? 雖然介紹完了KMP算法的標(biāo)準(zhǔn)形式,但是,我發(fā)現(xiàn)在實(shí)際的操作中,有一些方面并不是很好操作,比如t[0],s[0]為字符串的長(zhǎng)度,這里就需要進(jìn)行一些別的操作實(shí)現(xiàn),s[0],t[0]為字符串長(zhǎng)度,麻煩了。在最后給出我在后面改進(jìn)的KMP改良算法。希望大家在前面的內(nèi)容看明白以后,來(lái)看看這個(gè)改良版本的算法。
using namespace std;void get_nextval(string t, int* nextval){int i = 1;int j = 0;int l = t.length();nextval[0] = -1;nextval[1] = 0;while (i{if (j==-1||t[i] == t[j]){++i;++j;if (t[i] != t[j])nextval[i] = j; elsenextval[i] = nextval[j];} elsej = nextval[j];}}int kmp(string s, string t, int pos){int l1 = s.length();int l2 = t.length();int nextval[255];get_nextval(t, nextval);int i = pos;int j = 0;while (i < l1&&j{if (j==-1||s[i] == t[j]){i++;j++;} elsej = nextval[j];}if (j ==l2)return i - l2; elsereturn -1;}void main(){string s, t;int pos;cout << "請(qǐng)輸入主句"<<endl;cin >> s;cout << "請(qǐng)輸入查找句"<<endl;cin >> t;cout << "請(qǐng)輸入從哪一個(gè)字符開(kāi)始查找(第一個(gè)字符的位置為0)"<<endl;cin >> pos;cout << "查找句位于" << kmp(s, t, pos);}
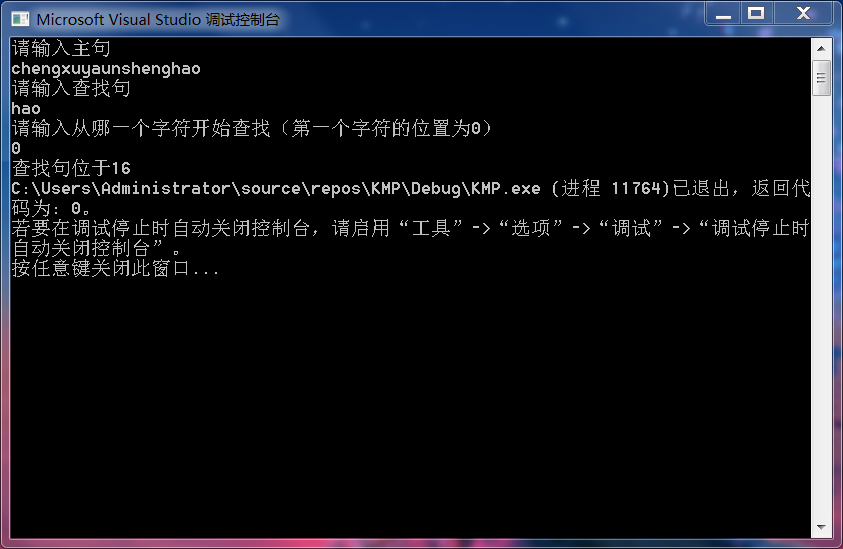
???快過(guò)年了,小編在這里給各位看客老爺們提前說(shuō)一聲,祝大家新年快樂(lè)!
如果你對(duì)該篇文章存在任何疑問(wèn)
歡迎提出您的建議
E-meal:[email protected]
?掃碼關(guān)注我們
