99精品免费视频在线观看,亚洲人妻视频,中文字幕在线欧美,日日摸日日操,国产久久色视频,国产公妇乱婬XXXX看一本毛片,淫荡日逼,中文字幕无码日韩专区免费

貢獻(xiàn)者：天驕，小豬呼嚕，沐風(fēng)，楊夕，芙蕖，李玲

NLP論文學(xué)習(xí)筆記：https://github.com/km1994/nlp_paper_study

個人介紹：大佬們好，我叫楊夕，該項目主要是本人在研讀頂會論文和復(fù)現(xiàn)經(jīng)典論文過程中，所見、所思、所想、所聞，可能存在一些理解錯誤，希望大佬們多多指正。

NLP 百面百搭地址：https://github.com/km1994/NLP-Interview-Notes

推薦系統(tǒng) 百面百搭地址：https://github.com/km1994/RES-Interview-Notes

關(guān)注公眾號【關(guān)于NLP那些你不知道的事】加入【NLP && 推薦學(xué)習(xí)群】一起學(xué)習(xí)！！！

昨天更新了【關(guān)于 CNN】那些你不知道的事(上)，今天繼續(xù)更新下篇

四、CNN 整體篇

4.1 CNN 的流程是什么？

s1 輸入變長的字符串或單詞串
s2 利用滑動窗口加池化的方式將原先的輸入轉(zhuǎn)化為固長的向量表示

4.2 CNN 的特點是什么？

CNN 能夠捕獲文本中的局部特征

4.3 卷積神經(jīng)網(wǎng)絡(luò)為什么會具有平移不變性？

平移不變性：即目標(biāo)在空間內(nèi)發(fā)生平移，但是結(jié)果（標(biāo)簽）不變

平移不變性=卷積+最大池化。卷積層具有平移等變性，池化層具有平移不變性。卷積神經(jīng)網(wǎng)絡(luò)的平移不變性，是池化層賦予的。

如果一個函數(shù)滿足“輸入改變，輸出也以同樣的方式進(jìn)行改變”這一性質(zhì)，我們就說該函數(shù)是等變的（equivariant）。形式化地，如果函數(shù)$f(x)$與$g(x)$滿足$f(g(x))=g(f(x))$，我們就說$f(x)$對于變換$g$具有等變性。

卷積層具有平移等變性，也就是說卷積層對平移是敏感的，輸入的平移能等價地影響輸出。直觀地，如果把一張輸入圖像先平移后卷積，其結(jié)果與先卷積后平移效果是一樣的。如果我們移動輸入圖像中的物體，它的表示也會在輸出中移動同樣的量。

卷積層的參數(shù)共享（Parameter Sharing）特性使得卷積層具有平移等變性。參數(shù)共享是指在一個模型的多個函數(shù)中使用相同的參數(shù)。在傳統(tǒng)的神經(jīng)網(wǎng)絡(luò)中，當(dāng)計算一層的輸出時，權(quán)重矩陣的每個元素只使用一次。當(dāng)它乘以輸入的一個元素后，就再也不會用到了。但是在卷積神經(jīng)網(wǎng)絡(luò)中，卷積核的每一個元素都作用在輸入的每一個位置上。卷積運算中的參數(shù)共享保證了我們只需要學(xué)習(xí)一個參數(shù)集合，而不是對于每個位置都需要學(xué)習(xí)一個單獨的參數(shù)集合。

如果一個函數(shù)滿足“輸入改變，輸出不會受影響”這一性質(zhì)，我們就說該函數(shù)是不變的（invariant）。形式化地，如果函數(shù)$f(x)$與$g(x)$滿足$g(x)=x'$且$f(x)=f(x')=f(g(x))$，我們就說$f(x)$對于變換$g$具有不變性。

池化層具有（近似）平移不變性，也就是說池化層對平移不敏感。不管采用什么樣的池化函數(shù)，當(dāng)輸入做出少量平移時，池化能夠幫助輸入的表示近似不變。例如我們使用最大池化，只要變換不影響到最大值，我們的池化結(jié)果不會收到影響。對于一個卷積核來說，只有一個值的變動會影響到輸出，其他的變換都不會造成擾動。平均池化的近似不變性就稍弱些。

局部平移不變性是一個很有用的性質(zhì)，尤其是當(dāng)我們關(guān)心某個特征是否出現(xiàn)而不關(guān)心它出現(xiàn)的具體位置時。

4.4 卷積神經(jīng)網(wǎng)絡(luò)中im2col是如何實現(xiàn)的？

卷積的運算量十分巨大，如果將卷積運算轉(zhuǎn)化為矩陣運算，便能利用GPU來提升性能。

im2col全稱image to column（從圖像到矩陣），作用為加速卷積運算。即把包含批數(shù)量的4維數(shù)據(jù)轉(zhuǎn)換成2維數(shù)據(jù)。也就是將輸入數(shù)據(jù)降維，然后通過numpy的矩陣運算后得到結(jié)果，再將結(jié)果的形狀還原，從而通過用矩陣運算來代替for循環(huán)語句。

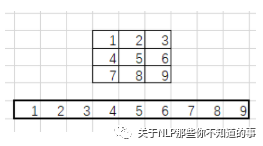
im2col將卷積核和卷積核掃過的區(qū)域都轉(zhuǎn)化為列(行)向量。舉個例子方便理解：

假設(shè)一個3*3卷積核為：

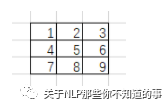
輸入圖像是5*5像素的單通道圖像：

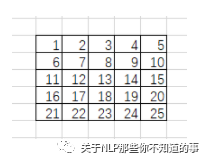
卷積核會鎖定3*3的滑動窗口：

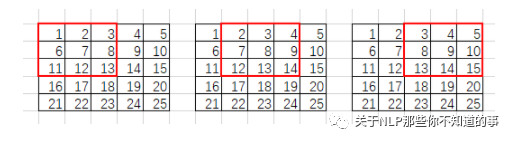
im2col會將每個滑動窗口內(nèi)的像素轉(zhuǎn)為列向量：

就這樣轉(zhuǎn)化所有滑動窗口的列向量，將其拼接成9行的矩陣（行數(shù)與滑動窗口數(shù)目相關(guān)，列數(shù)則與卷積核大小相關(guān)）：

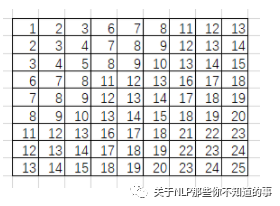
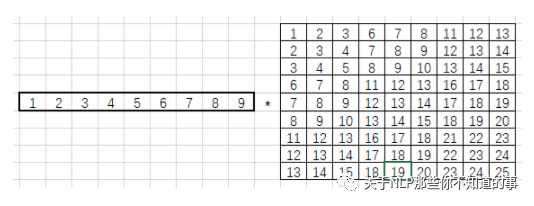
im2col還會將卷積核轉(zhuǎn)化為行向量：

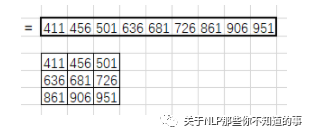
最后使用卷積核行向量乘以滑動窗口元素組成的矩陣：

得到1*9的列向量，將其拼接成特征圖：

4.5 CNN 的局限性是什么？

以CNN為代表的前饋神經(jīng)網(wǎng)絡(luò)使用了條件獨立假設(shè)，其特征提取范圍受到限制；而循環(huán)神經(jīng)網(wǎng)絡(luò)或者Attention機(jī)制的模型能夠看到序列整體的信息，因此對于序列建模任務(wù)，單純的CNN存在先天不足。
卷積神經(jīng)網(wǎng)絡(luò)的核心思想是捕捉局部特征。對于序列任務(wù)，比如文本來說，局部特征就是由若干單詞組成的滑動窗口（類似N-Gram）。卷積神經(jīng)網(wǎng)絡(luò)的優(yōu)勢在于能夠自動地對N-Gram特征進(jìn)行組合和篩選，獲得不同抽象層次的語義信息。

解決方法：加入更多卷積層 -> 網(wǎng)絡(luò)深度增加 -> 參數(shù)量增大 -> 容易過擬合 -> 引入 Dropout 正則化 -> 引入超參數(shù) -> 網(wǎng)絡(luò)龐大冗余，難以訓(xùn)練

使用CNN做序列任務(wù)的優(yōu)點在于其共享權(quán)重的機(jī)制，使得訓(xùn)練速度相對較快；但是其最大的缺點在于CNN無法構(gòu)建長距離依存關(guān)系。
有許多研究者試圖改進(jìn)CNN模型，使其能夠應(yīng)用于序列任務(wù)。諸如用于句子語義建模的動態(tài)卷積神經(jīng)網(wǎng)絡(luò)DCNN、可以在整個序列的所有窗口上進(jìn)行卷積的時延神經(jīng)網(wǎng)絡(luò)TDNN等。

五、Iterated Dilated CNN 篇

5.1 什么是 Dilated CNN 空洞卷積？

動機(jī)：

正常CNN 的 filler 作用于輸入矩陣連續(xù)位置，利用卷積和池化整合多尺度的上下文信息，導(dǎo)致分辨率損失
pooling 會損失信息，降低精度，不加則導(dǎo)致感受野變小，學(xué)不到全局信息
CNN提取特征的能力受到卷積核大小的限制，特別是對于序列問題，容易造成長距離依賴問題

介紹：Dilated Convolutions，翻譯為擴(kuò)張卷積或空洞卷積。空洞卷積與普通的卷積相比，除了卷積核的大小以外，還有一個擴(kuò)張率參數(shù)，主要用來表示擴(kuò)張的大小，以及去掉 pooling。
空洞卷積與普通卷積的相同點：卷積核的大小是一樣的，在神經(jīng)網(wǎng)絡(luò)中即參數(shù)數(shù)量不變，區(qū)別在于擴(kuò)張卷積具有更大的感受野。感受野指的是特征圖上某個元素的計算受輸入圖像影響區(qū)域的范圍，即特征圖上神經(jīng)元能夠“看到”的圖像范圍，例如3×3卷積核的感受野大小為9。

具體地，空洞卷積通過給卷積核插入“空洞”變相增加其大小。如果在卷積核的每兩個元素之間插入$D-1$個空洞，該卷積核的有效大小為$K'=K+(K-1)\times (D-1)$。其中$K$為原始卷積核大小，$D$稱為膨脹率(擴(kuò)張率，dilation rate)。當(dāng)$D=1$時卷積核為普通的卷積核。

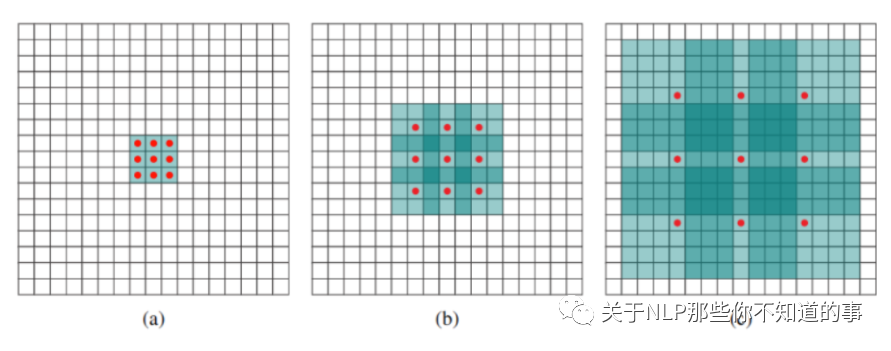
例如下圖中

(a) 普通卷積，1-dilated convolution，卷積核的感受野為3×3=9。
(b) 空洞卷積，2-dilated convolution，卷積核的感受野為7×7=49。
(c) 空洞卷積，4-dilated convolution，卷積核的感受野為15×15=225。

優(yōu)點：dilated width 會隨著層數(shù)增加而指數(shù)增加，層數(shù) 增加，參數(shù)量線性增長，感受野指數(shù)增加，可覆蓋全部信息

例如卷積核大小為3，步長為1，膨脹率為2的空洞卷積動態(tài)示意圖：

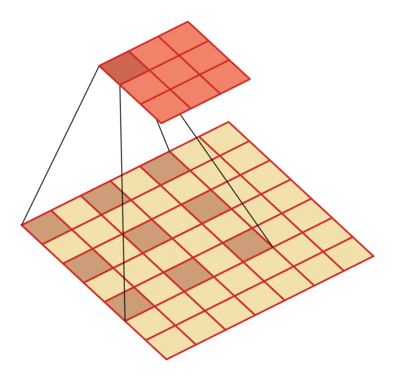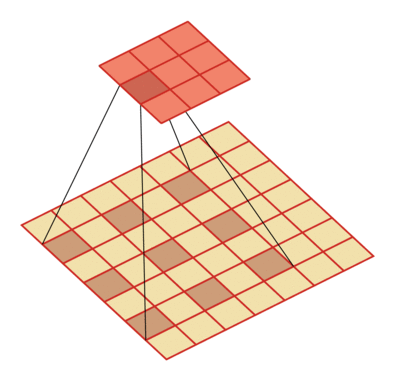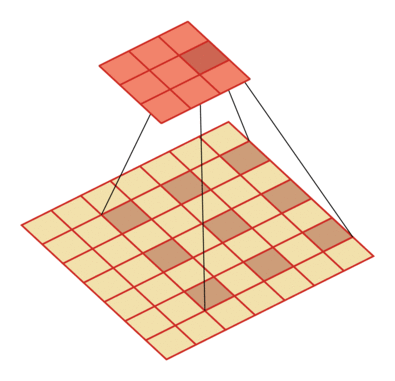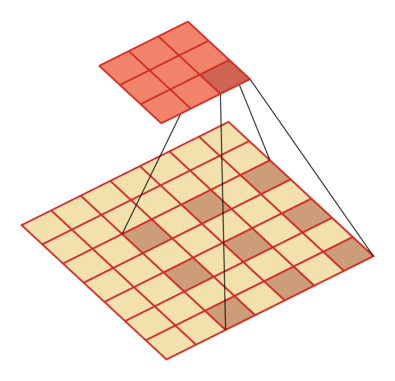
空洞卷積的作用

擴(kuò)大感受野。如果希望增加輸出單元的感受野，一般可以通過增加卷積核大小、增加卷積層數(shù)，或在卷積前增加池化操作來實現(xiàn)。但是前兩者會增加參數(shù)數(shù)目，第三種方式會損失信息。空洞卷積就是一種增加感受野的同時不增加參數(shù)數(shù)量的方法。
捕獲多尺度上下文信息：在進(jìn)行空洞卷積前，通過雙線性插值，對feature map進(jìn)行上采樣之后，再進(jìn)行空洞卷積，這樣可以在提高feature map的像素的同時，提取更多的全局信息

5.2 什么是 Iterated Dilated CNN？

思路：利用四個結(jié)構(gòu)相同的 Dilated CNN 拼接起來，每個 block 里面 dilated width 為 1，1，2 的三層 DCNN，能夠捕獲更大感受野的信息

六、反卷積篇

6.1 解釋反卷積的原理和用途？

1.反卷積原理

反卷積=上采樣=（轉(zhuǎn)置卷積+微步卷積）? 空洞卷積=一般意義上的廣義卷積（包含上采樣和下采樣）。

上采樣：在應(yīng)用在計算機(jī)視覺的深度學(xué)習(xí)領(lǐng)域，由于輸入圖像通過卷積神經(jīng)網(wǎng)絡(luò)(CNN)提取特征后，輸出的尺寸往往會變小，而有時我們需要將圖像恢復(fù)到原來的尺寸以便進(jìn)行進(jìn)一步的計算(e.g.:圖像的語義分割)，這個采用擴(kuò)大圖像尺寸，實現(xiàn)圖像由小分辨率到大分辨率的映射的操作，叫做上采樣(Upsample)。

反卷積是一種特殊的正向卷積，先按照一定的比例通過補0來擴(kuò)大輸入圖像的尺寸，接著旋轉(zhuǎn)卷積核，再進(jìn)行正向卷積。

反卷積又被稱為Transposed(轉(zhuǎn)置) Convolution，其實卷積層的前向傳播過程就是反卷積層的反向傳播過程，卷積層的反向傳播過程就是反卷積層的前向傳播過程。因為卷積層的前向反向計算分別為乘 $C$ 和 $C^T$,而反卷積層的前向反向計算分別為乘 $C^T$ 和 $(C^T)^T$，所以它們的前向傳播和反向傳播剛好交換過來。

上圖展示一個反卷積的工作過程，乍看一下好像反卷積和卷積的工作過程差不多，主要的區(qū)別在于反卷積輸出圖片的尺寸會大于輸入圖片的尺寸，通過增加padding來實現(xiàn)這一操作，上圖展示的是一個strides(步長)為1的反卷積。下面看一個strides不為1的反卷積

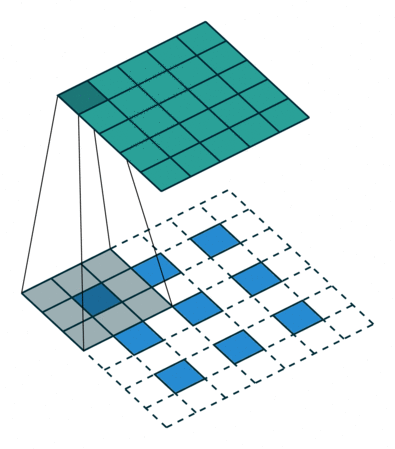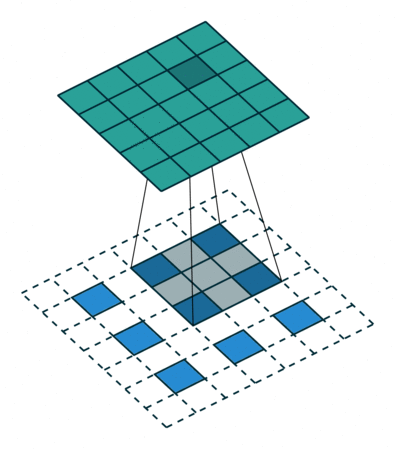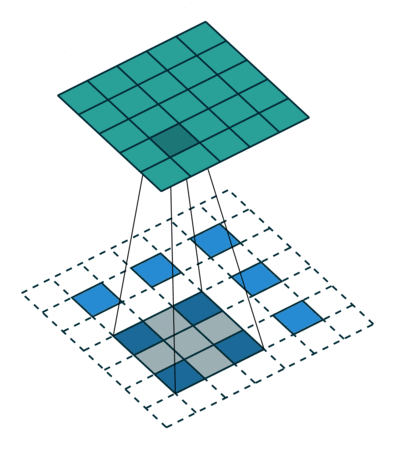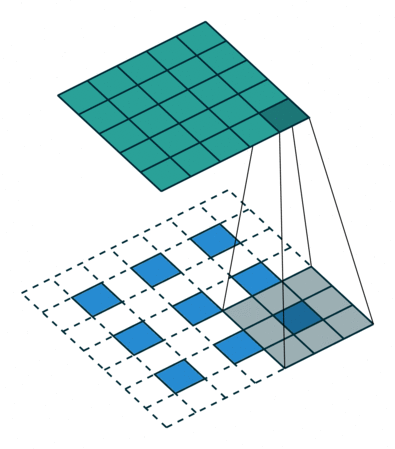
上圖中的反卷積的stride為2，通過間隔插入padding來實現(xiàn)的。同樣，可以根據(jù)反卷積的o、s、k、p參數(shù)來計算反卷積的輸出i，也就是卷積的輸入。公式如下：i=(o?1)?s+k?2?p。

2.作用

通過反卷積可以用來可視化卷積的過程
反卷積在GAN等領(lǐng)域中有著大量的應(yīng)用。比如用GANs生成圖片，其中的generator和discriminator均采用深度學(xué)習(xí)，generator生成圖片過程中采用的就是反卷積操作（當(dāng)然discriminator采用卷積對generator生成的圖片判別真?zhèn)危?/p>
將一些低分辨率的圖片轉(zhuǎn)換為高分辨率的圖片。

參考：

https://kknews.cc/code/zb2jr43.html

https://zhuanlan.zhihu.com/p/48501100